基于旅客选择行为的高速铁路平行车次定价策略
2018-12-28江文辉李延来
江文辉,李延来*,b
(西南交通大学a.交通运输与物流学院;b.综合交通运输智能化国家地方联合工程实验室,成都610031)
0 引言
我国高铁客运市场已培育了大量客流,且许多高速铁路线逐渐趋于“公交化”的运营特点,如京沪高铁全天共开行37对高速列车,平均每20 min就有1趟车次开行,这些平行车次之间存在很强的替代性,但现行高铁票价固定,忽略了平行车次由于发车时刻、旅行时间等方面的差异所导致旅客对平行车次间效用感知的不同,如:同等票价下,旅客更愿意选择上午08:00分出发12:34分到达的车次而非下午19:05分出发23:39分到达的车次;运行时间为4 h的车次比运行时间为6 h的车次更具吸引力.此外,现行票价又无法与实际客流状况相适应,不能有效引导和控制客流,最终导致了平行车次的上座率失衡与收益损失.因此,有必要对高速铁路平行车次的定价问题进行相应的理论和方法研究.
本文研究内容属于多产品定价范畴,研究背景主要集中在易逝品和民航业.文献[1]将GVR模型推广到多产品的情形,并利用强度控制理论首次研究了多产品的动态定价问题.文献[2]建立了多产品动态定价和库存控制的统一模型.文献[3]研究了存在纵向差异的多产品动态定价问题,采用线性效用函数来刻画消费者对产品的选择现象,在此基础上文献[4]利用MNL模型来描述顾客的选择行为,建立了多产品的动态定价和库存决策联合模型.文献[5]研究了多个平行航班的动态定价问题,并设计启发式算法,以解决模型“维数灾难”问题.文献[6-7]均建立了两平行航班的动态定价模型,文献[6]考虑了乘客分类,文献[7]重点放在求解算法的设计.
高铁定价问题最近引起许多学者的关注,文献[8]建立了考虑团体订票情形下的高速铁路动态定价模型,文献[9]利用最大凹向包络理论研究了高速铁路的动态定价问题,文献[10]在民航竞争环境下研究了高速铁路的动态定价,文献[8-10]的研究内容均是单列车的定价问题,不涉及平行车次问题.针对上述不足,本文将借鉴多产品定价理论和民航业的成功实践,并充分考虑旅客需求状况和平行车次间的质量差异属性,以平行车次的整体收益最大化为目标提出了差别动态定价、最优固定价格和统一动态定价3种定价策略,并对比3种定价策略的优劣.
1 问题描述
考虑特定时间段内(如1天)运行在两城市之间的n列平行高铁,N={1,2,…,n}表示车次集合.由于平行车次间的发车时间间隔相对于整个车票预售期可忽略不计,可认为n列平行高铁的车票预售期相同,将整个预售期划分为T个时段,保证每个时段至多只有1个乘客到达且至多只预定1张车票,设到达率为λ,t=1开始售票,t=T是车票预订的最后一个时段.C=(C1,C2,…,Cn)为平行车次初始车票数量,pt=(p1t,p2t,…,pnt)为t时段各平行车次的票价,ℛ为可选价格集合.若t时段车次i的席位已售完,则剩余预售时段将其票价设置为空价格(p∞),不考虑退票和超订等情形.
如前文所述,对于相同票价的平行车次,旅客通常对不同车次的效用感知是不同的,即平行车次间存在不同程度的质量差异,最终导致旅客在不同车次间存在选择行为.本文利用MNL模型[4-5,11]来描述旅客这种选择行为.具体地,t时段到达的旅客以pit的票价预定i车次席位所获得的效用Ui可表示为
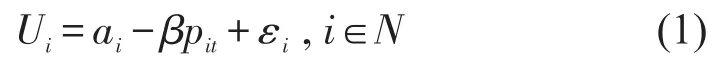
式中:ai为常量,表示车次i的质量水平,可用发车时间点、旅途时间等因素测量获得;β表示价格弹性系数,反应了旅客对票价的敏感程度;εi为随机变量,服从Gumbel分布,均值为0和规模参数μ=1,若到达的旅客不选择任何车次时获得效用为U0=ε0.
用qit(pt)表示t时段到达的旅客选择车次i∈N的概率,q0t(pt)表示到达旅客不选择任何车次的概率,且满足,则有
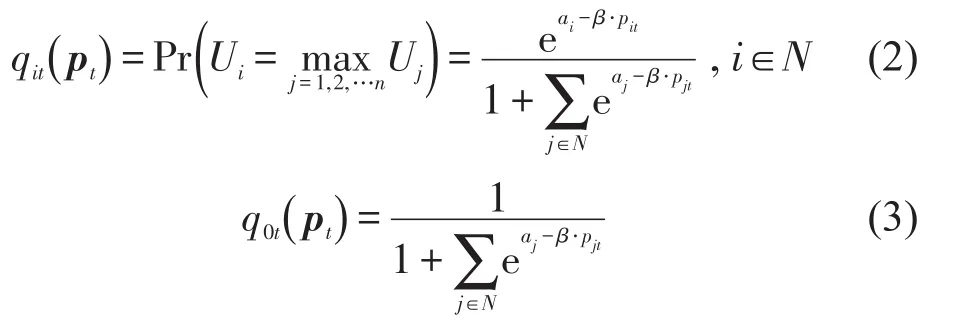
若t时段车次i∈N的票价设置为p∞,表示席位已售完不再接受订票请求qit(pt)=0.
从城市个体来看,临沂、连云港、济宁、泰安和日照的城镇化与旅游经济耦合度长期处于高水平,虽然10年间有所波动变化,但始终处于高水平阶段,并未影响这些城市在淮海经济区的领先地位.徐州与淮安相似,大部分时间处于高水平,但2008~2011年受金融危机影响较大,出现了明显下降,甚至跌入磨合的水平,2012开始回升,但在同类高水平城市中排名靠后.莱芜、宿迁、菏泽、枣庄、蚌埠和商丘的城镇化与旅游经济耦合度在淮海经济区处于低值,且在10年间波动起伏较多、较大.其余城市在2005~2015年,都在拮抗、磨合与高水平阶段内存在着较多波动.
2 高速铁路平行车次定价策略研究
高速铁路平行车次现行票价机制存在3点不足:①高速铁路平行车次在发车时刻、运行时间等方面存在明显区别,但现行票价机制模糊了这种差异;②现行票价机制实质是单独优化某一列高速铁路的收入,缺乏整体性;③票价固定,无法与实际客流状况相适应.基于此,我们将提出3种定价策略.
2.1 差别动态定价策略
差别动态定价是在任意t时段同时为各个车次设定票价,即决策价格向量记表示t时段票额状态为时,n列平行高铁在剩余售票周期[t,T]内可获得的最大期望收益,建立差别动态定价模型为表示车次i的席位期望
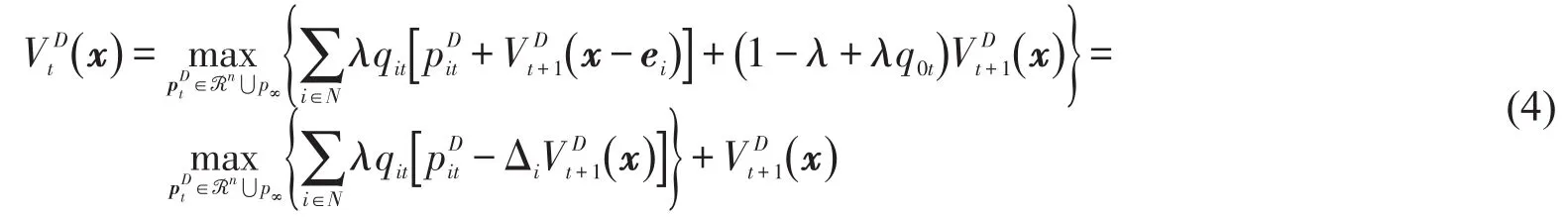
式中:ei表示第i项为1,其余项均为0的n维向量;边际收益,边界条件为.
由式(4)可知,t时段的票价决策与t+1时段的状态无关,由此可定义为
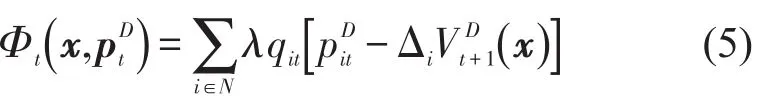
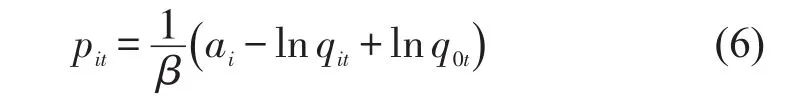
定义qt=(q1t,q2t,…,qnt,q0t),将式(6)代入式(5)可得
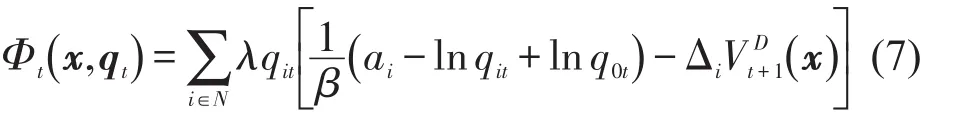
定理1对于给定的车票预售时段t和车票状态xt,车次i∈N的最优票价为
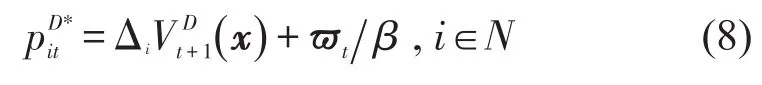
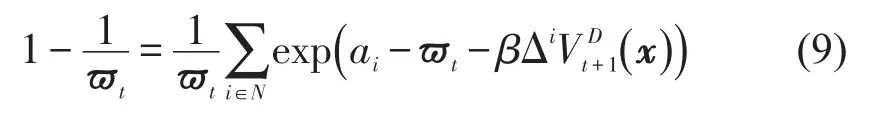
证明先证是关于q的凹函数,t.由式(7)可求得函数的黑塞矩阵为
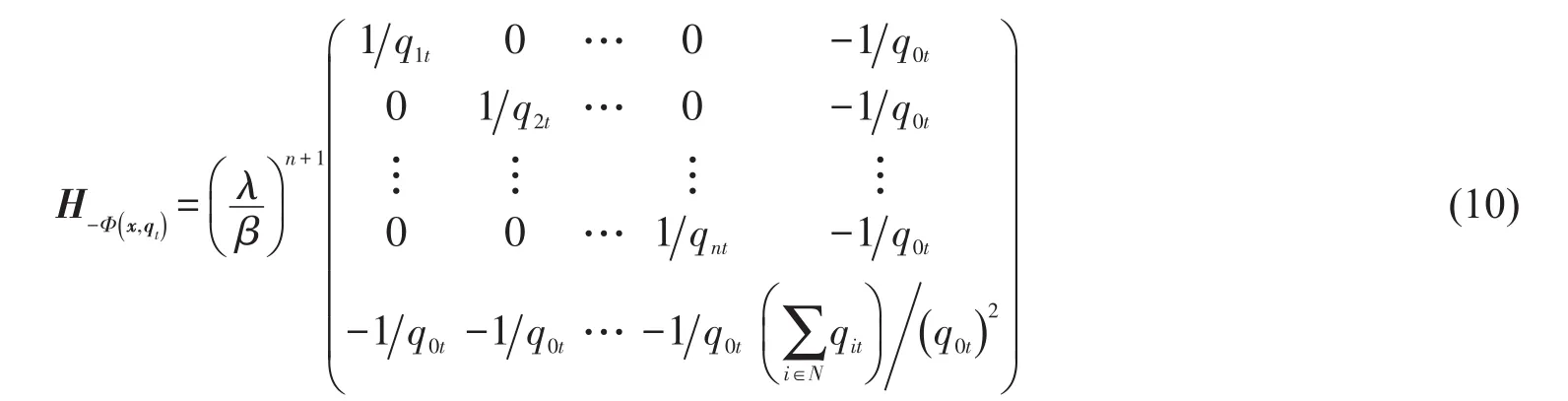
对于非零向量y=(y1,y2,…,yn+1)有
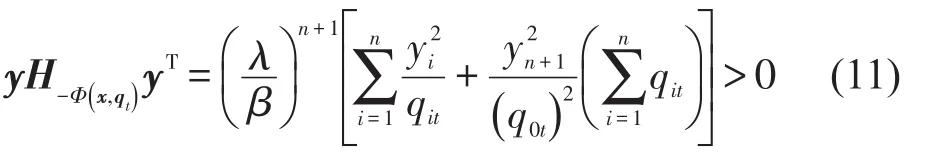
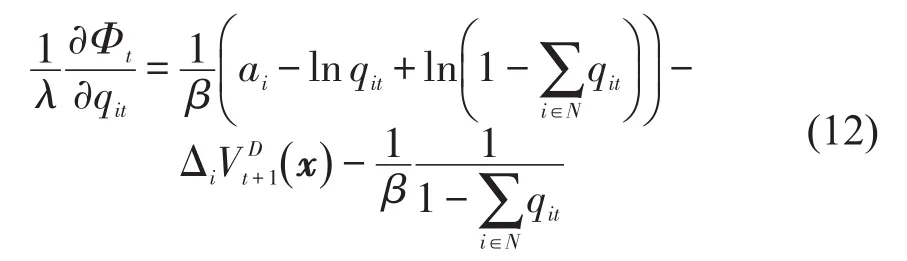
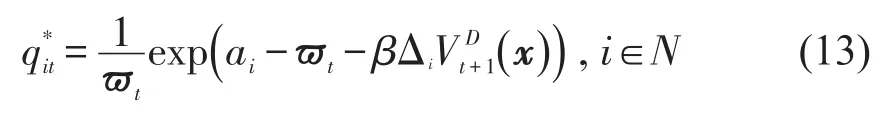
将式(13)带入式(6)可得到等式(8)成立,联立式(13)和消去可得到ϖt满足的式(9),最后说明ϖt是式(9)的唯一解,令g(ϖt)为
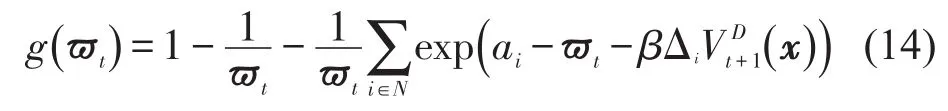
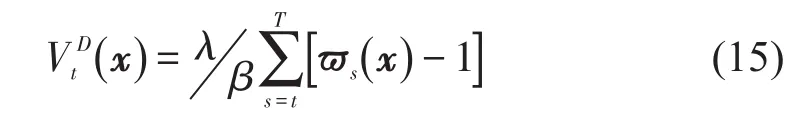
2.2 最优固定价格策略
最优固定价格策略是在售票开始前,根据预测的客流状况为不同车次制定不同票价,在整个售票周期不再做票价调整.该定价策略有别于现行的票价机制,其充分考虑了各车次的旅客需求状况和车次间的质量差异属性.可知任意t时段,车次i∈N售出1张席位的概率为λqit(pt),则整个车票预售期,车次i的总需求可用泊松分布来描述,其到达强度为λqit(pt)T.记VF(C)为最优固定价格策略下的最大期望收益,为该策略下的最优票价向量,则建立最优固定价格定价模型为
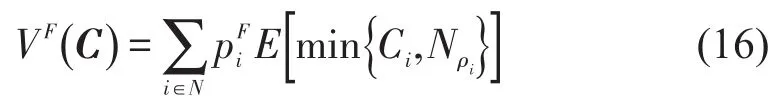
式中:Nρi表示车次i(i∈N)在剩余销售周期内的席位需求量,服从参数为ρi=λqi(pl)T的泊松分布.因此,可通过非线性优化方法求解式(17),得到该策略下最优票价.
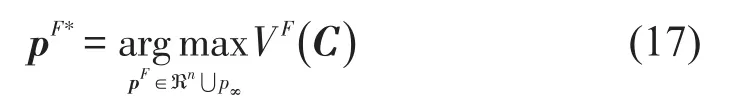
2.3 统一动态定价策略
统一动态定价仅对票价进行实时动态更新,而不考虑对平行车次的差异,即所有平行车次的票价相同.记为统一动态定价策略下的期望收益,为该策略下任意时段的票价,建立统一动态定价的模型为
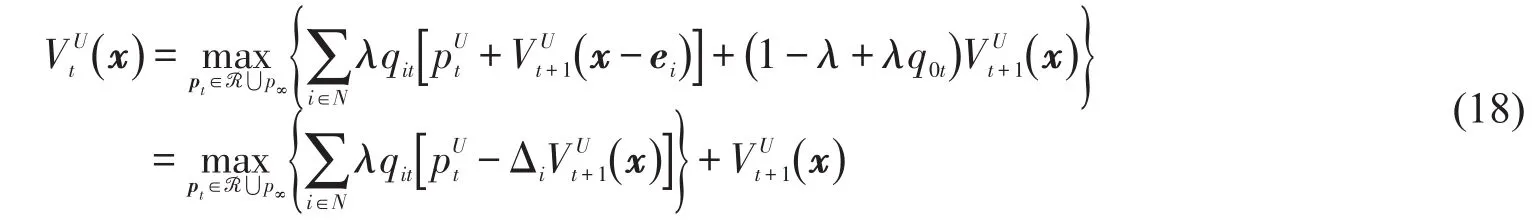
3 案例分析
以京沪高铁为案例背景,京沪线全长1 318 km,目前北京—上海全天共开行37列平行高铁,发车时刻分布在06:43-19:05,全程运行时间最短为264 min,最长为372 min,现行票价二等座均为553元(仅考虑二等座).参考我国高铁票价现状,京沪高铁单位里程运价率为0.420元/km;西武高铁为0.432元/km;其中单位里程运价率最低的是京广高铁0.376元/km,最高的是广深高铁0.730元/km.因此将京沪铁路的单位里程运价率的浮动范围定为0.30~0.75元/km是合理的,折合成票价约为396~989元.为了便于标定平行车次的质量水平ai,进一步将目前京沪高铁二等座票价553元标准化为“10”,即票价的浮动范围转化为7.16~17.88.
3.1 旅客购票过程的最优票价路径分析
不失一般性,考虑运行在京沪高速铁路线上的2列平行车次1和2,目前剩余席位数量均为C1=C2=10,剩余售票时段T=100,旅客的票价敏感系数β=0.6.图1为基于3种定价策略对不同情形下旅客购票过程的最优票价路径进行了仿真分析.
由图1可知,当潜在到达旅客数量较少时(图1(a)),在整个售票过程中3种定价策略的最优票价均低于当前票价“10”,当潜在到达旅客数量较大时(图1(b)和图1(c)),3种定价策略都相应地提高票价(出现票价高于当前票价“10”),说明3种定价策略均以实际客流状况为导向,而现行票价已与实际客流市场脱轨.此外,还可以看出:
(1)差别动态定价和最优固定价格策略均证实平行车次最优票价差异会使随着平行车次质量差异的增大而增大,因此适当增加高质量水平车次(运行时间短、早上发车中午到达)的票价,对低质量水平车次(运行时间较长、下午发车深夜到达)提供一定的折扣,可以引导客流,平衡车次间上座率.
(2)当潜在到达旅客数量较大时(图1(b)和图1(c)),高质量水平的列车(车次1)会率先售空座位,所以铁路部门在对平行车次进行票额分配时,应考虑平行列车间的差异化,科学的分配给高质量水平车次更多的票额,可以提高整体上座率并增加售票收入.
(3)图1(b)和图1(c)中统一动态定价策略下的最优票价路径出现向下跳跃现象,原因是,统一动态定价策略下,旅客偏好选择高质量属性的车次(车次1)直到车票售完,而低质量属性的车次(车次2)尚有大量的席位未售出,为尽快在列车开行前售空车票,会大幅度降低票价来吸引旅客,提高低质量属性车次的上座率.
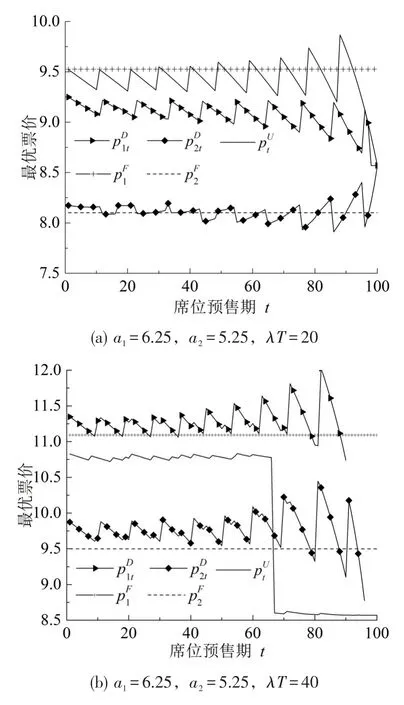
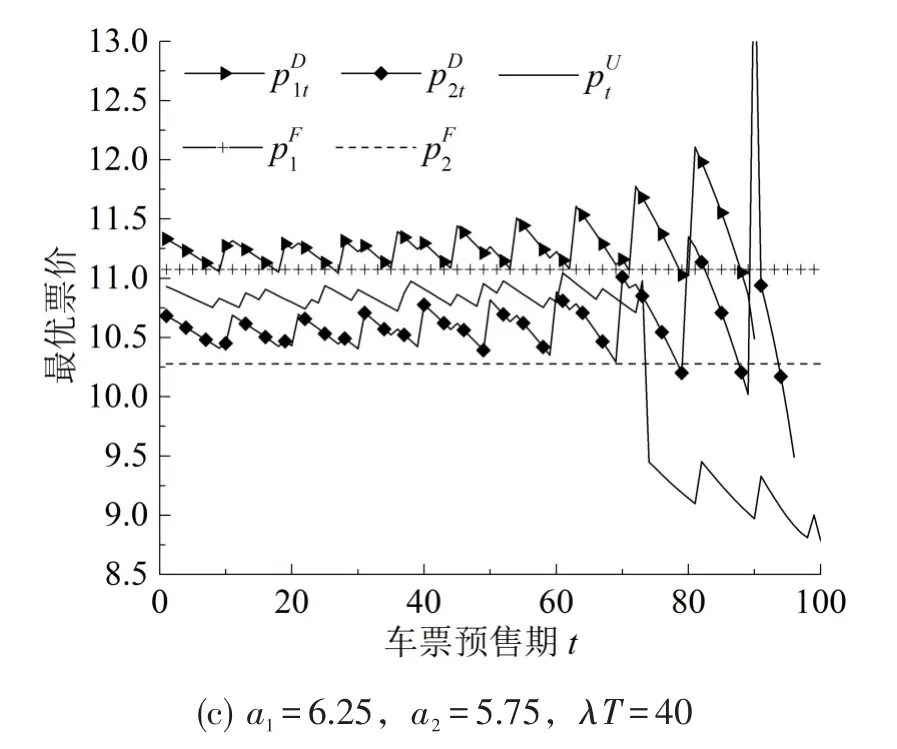
图1 不同情形下旅客购票过程最优票价路径Fig.1 The optimal fare path for passengers to purchase tickets under different circumstances
3.2 不同情形下3种定价策略效率对比分析
仍采用上述基础数据,分析不同情形下3种定价策略的效率.表1,图2,图3和表2,图4,图5分别给出了不同旅客需求环境下或两平行车次在不同质量水平组合条件下3种定价策略的最大期望收益、售出席位数量和平均票价水平的对比结果.
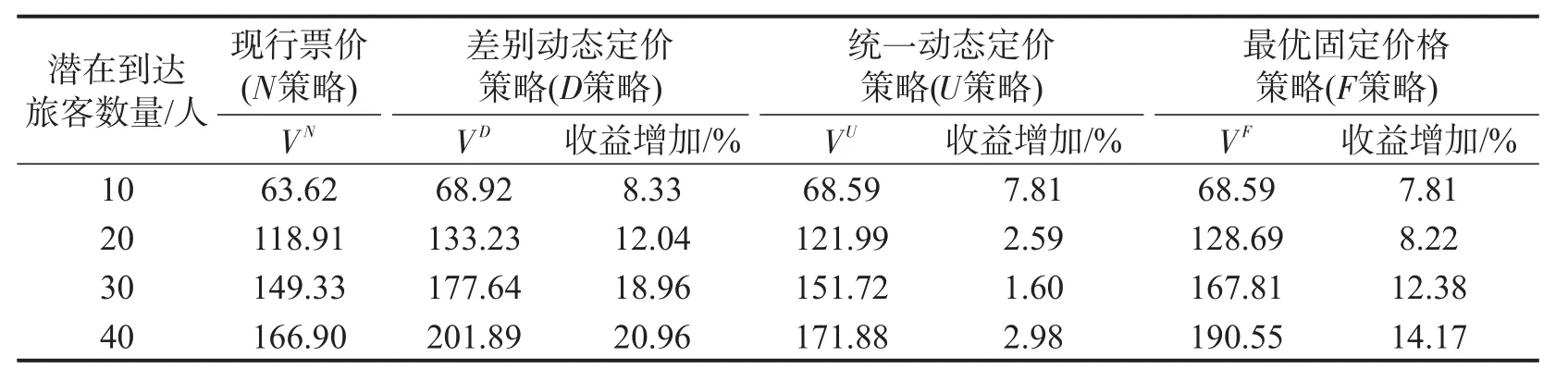
表1 不同旅客需求环境下3种定价策略的最大期望收益对比(a1=6.25,a2=5.25)Table 1 The comparison of three pricing strategies in different passenger demand environment(a1=6.25,a2=5.25)
由表1可知,4种需求环境下,3种定价策略均能使收益增加,最多可增加20.96%的收益.其中D策略在所有情况下表现都是最优的,其他两种定价策略在旅客需求较少(λT=10)的环境下表现的相对较好,但随着潜在到达旅客数量的增加,效率逐渐降低.易知,平行车次的最优票价与两个因素有关:①列车间的质量差异水平;②实时需求信息和席位状态信息.D策略能够同时兼顾两个因素所以具有最好的绩效,而U策略和F策略只是单方面利用了某个因素,所以均不能取得最好的效率.此外,F策略表现要优于U策略,说明当平行车次间存在较高质量差异时,有必要实施差别定价.
由图2和图3可知,同等旅客需求环境下,D策略在平衡车次间上座率和提高总体上座率上仍具有很好的优势,且能以相对较低的平均票价水平获得最大的期望收益.F策略在平衡列车间上座率和总体上座率上也表现很好,但当潜在到达旅客数量为40人时,采用D策略和F策略均能使两列车售空所有席位,但是D策略可以使售票收入额外增加6.79%.U策略和现行票价机制获得了较差的上座率,且平均票价较高,这种现象不利于高铁客运 市场的可持续发展.
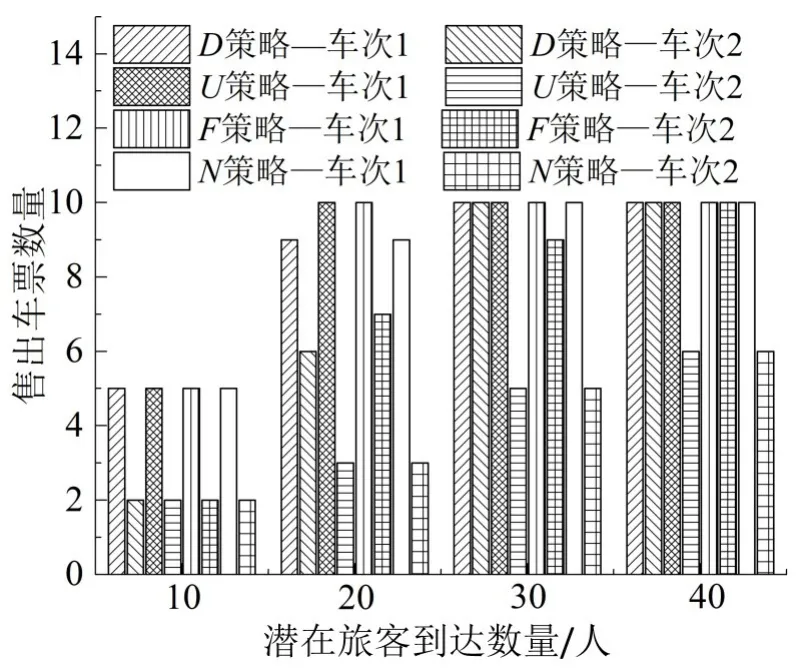
图2 不同旅客需求环境下两平行车次售出车票数量(a1=6.25,a2=5.25)Fig.2 Number of tickets sold by two parallel trains in different demand environment(a1=6.25,a2=5.25)
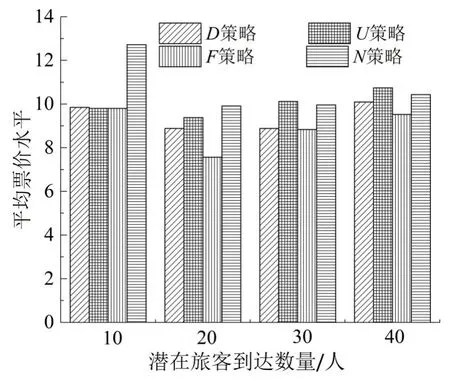
图3 不同旅客需求环境下的平均票价水平(a1=6.25,a2=5.25)Fig.3 Average fare in different passenger demand environment(a1=6.25,a2=5.25)
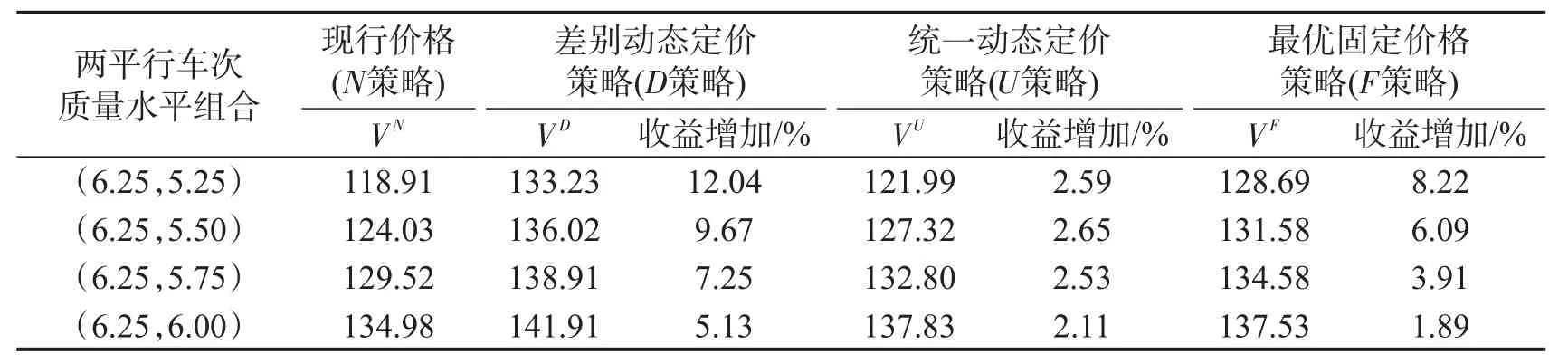
表2 不同质量水平差异条件下3种定价策略最大期望收益对比(λT=20)Table 2 The comparison of three pricing strategies under under different quality levels(λT=20)
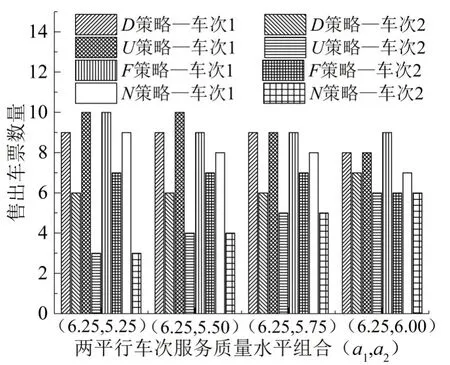
图4 不同质量水平组合下两平行车次售出车票数量Fig.4 Number of tickets sold by two parallel trains in different quality levels
同样由表2可知,不同质量水平差异组合下,D策略仍然表现最好,其他两种定价策略也能使得售票收入得到不同程度的提高.随着两平行车次质量水平差异的缩小,U策略逐渐凸显优势,当质量水平组合为(6.25,6.00)时,U策略要优于F策略,且与D策略相比收益差距逐渐缩小.因此,铁路部门在为质量水平差异较小(如发车时间间隔较短或全程运行时间相等)的平行车次制定票价时,可以适当忽略车次间的质量差异水平对票价的影响,采用U策略以降低分别优化平行车次票价的难度.
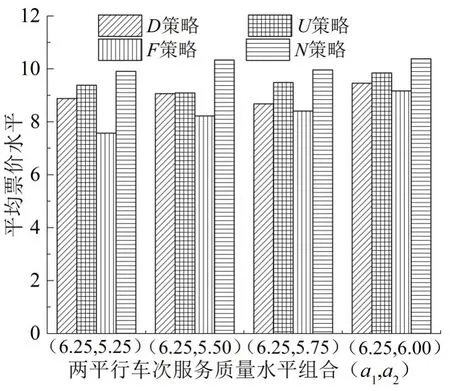
图5 不同质量水平组合下的平均票价水平Fig.5 Average fare in different quality levels
从图4可以看出,随着平行车次质量水平差异的缩小,车次间的上座率逐渐达到均衡,表明车次间质量水平的差异是影响上座率不均衡的主要因素,铁路部门应充分关注这一因素来实施售票前期的票额分配工作.进一步由图5可知,在不同质量水平差异组合下,3种定价策略的平均票价水平并不稳定,说明除旅客需求强度外,列车间的质量差异水平也是影响票价变化的内因.
4 结论
以高速铁路平行车次由于发车时刻、旅行时间等因素所导致质量差异为切入点,本文研究了平行车次的定价问题,并以平行列车的整体收入最大化为目标提出了3种定价策略.通过算例分析表明:3种定价策略均能有效提高售票收入,其中差别动态定价策略表现最优,而最优固定价格策略和统一动态定价策略的相对优劣与平行车次间质量差异大小和潜在到达旅客数量有关.本文的研究内容进一步完善了高速铁路平行车次定价理论.此外,民航作为高铁的最大竞争者,进一步研究民航竞争环境下的高速铁路定价问题具有重大现实意义.
