悬链线形断面正常水深的直接计算公式

许晓阳 ，张根广，陈学彪，刘 余，张子钰

(西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100)

悬链线形断面不仅具有在施工、制模中易于计算和控制的优点，还具有防止土基冻胀破坏、抵抗外水压力、受力条件好、输沙率高、过水能力强及抵抗冲刷性能好等优点[1,2]，因此，悬链线形渠道在水利水电和灌溉排水工程中得到越来越广泛的应用。

正常水深是工程设计和水力计算中一个重要参数，在实际工程中应用频繁，且有很高的精度要求。近年来，国内外学者对一些简单过水断面正常水深的分析计算进行了深入研究，取得了较为丰富的研究成果，例如梯形断面[3-6]、抛物线形断面[7-12]和圆形断面[13-15]等。对于悬链线形断面正常水深，设计流量相应正常水深有解析解公式，如冯雪等[1]公式和黄开路等[16]公式，而非设计流量相应正常水深的计算需求解超越方程，在理论上无法直接求解，目前，仅有三家公式可供参考，即黄开路等[16]根据数学分析和水力学原理，得到悬链线形横断面正常水深求解的迭代公式，需反复迭代3～4次方可达到精度要求；滕凯[17]通过引入恰当的无量纲水深参数，对悬链线形断面正常水深基本方程进行数学变换，采用优化拟合的方法得到近似计算公式；文辉等[18]通过对悬链线形断面均匀流基本方程进行数学变换，对引入的无量纲参数与无量纲水深的关系进行分析，应用优化拟合原理得到拟合计算公式，计算精度不高是上述3家公式普遍存在的问题。综上所述，有必要对悬链线形断面正常水深的计算做进一步的研究。首先，依据悬链线形断面几何特征、水力要素和正常水深基本方程，得到设计流量相应正常水深的解析解公式；其次，对于非设计流量相应正常水深，通过引入恰当的无量纲参数，导出悬链线形渠道正常水深的迭代计算公式，同时利用优化拟合原理得到初值计算公式，将初值函数代入迭代计算公式得到正常水深直接计算公式。

1 正常水深的基本计算公式

根据《水力学》[19]知，正常水深的基本方程为：

(1)

式中：Q为渠道通过流量，m3/s；WP为湿周，m；A为过水断面面积，m2；n为渠道糙率系数；i为渠道设计坡降。

1.1 悬链线形断面几何特征及水力要素

悬链线形断面过水断面如图1所示。

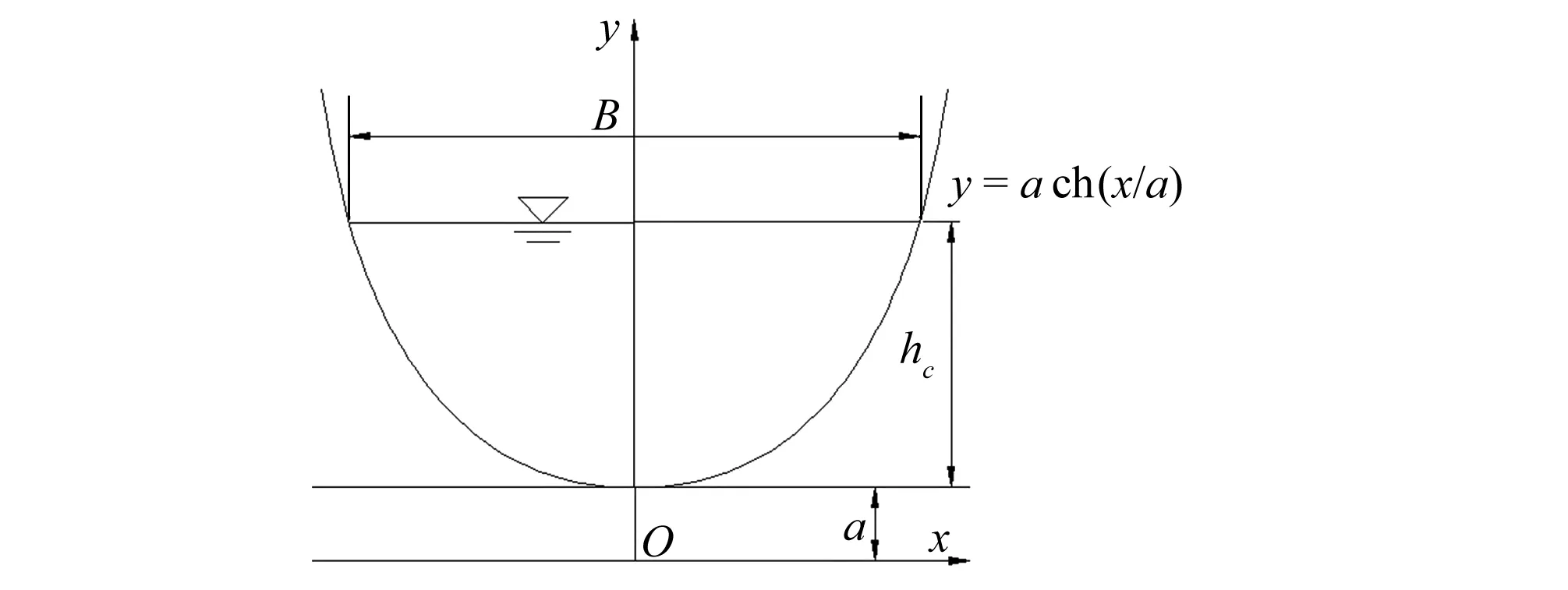
图1 悬链线形过水断面Fig.1 catenary-shaped cross section

悬链线形断面过水断面曲线方程为：

(2)

设过水断面宽度为B，则过水断面水力要素分别为：

(3)

(4)

(5)

式中：a为悬链线形断面形状参数。

由式(5)可得：

(7)

(8)

将式(8)代入式(3)可得：

(9)

将式(6)、(7)、(8)代入式(4)可得：

(10)

1.2 悬链线形断面设计流量相应正常水深的解析解

在设计悬链线形断面时，a通常不给定，而是给出设计流量相应正常水深的水面宽度B和a的比值η，即B/a=η。

将式(3)、(4)代入式(1)，整理得：

(11)

由式(11)可直接求得a的值，进而可由式(5)直接计算正常水深h的值，即：

(12)

在悬链线形断面的设计中，根据要求选定η的值，然后将n、Q、i、η的值代入式(12)，即可求得设计流量相应正常水深h的值。

1.3 悬链线形断面非设计流量相应正常水深公式的推导

将式(9)、(10)代入式(1)，整理可得：

(13)

为方便分析，令：

(14)

式中：u为无量纲正常水深；k为无量纲综合参数。

将式(14)代入式(13)整理可得：

(15)

式(15)为悬链线形断面非设计流量相应正常水深的基本计算公式，即相应正常水深h的隐函数方程。

2 悬链线形断面非设计流量相应正常水深的直接计算公式

2.1 无量纲正常水深u的取值范围

由文献[4]知，悬链线形断面为水力最佳断面的条件是：h/a=1.592 1，即u=2.592 1。在设计中为同时获得优良的水力学条件和较好的经济性，应该综合考虑水力最佳断面和经济最优断面这两个因素，本文考虑这一工程实际，以h/a=1.592 1为中心，延展其取值范围[h/5a,5h/a]=[0.318,7.961]作为h/a的取值范围，而对于悬链线形断面非设计流量的正常水深，取u∈[1.3,9.0]作为本文公式的适用范围。

2.2 正常水深的迭代计算公式

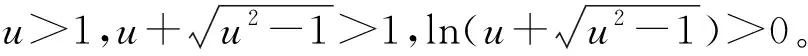
由式(15)整理可得迭代公式为：

(16)

2.3 迭代公式收敛性的判断

由《数值分析》[20]知，对于局部收敛的判断条件为：u=φ(u)有不动点u*，若存在u*的某个邻域|u-u*|≤δ，使迭代函数的一阶导数在该邻域内连续，且|φ′(u*)|<1，则该邻域内任一点为初值的迭代都收敛于u*。

令：

(17)

对式(17)进行一阶求导可得：

(18)

将式(15)代入式(18)整理可得：

(19)

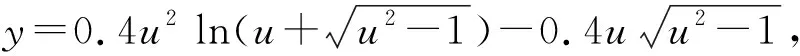
(20)

对y求极限：

(21)

由式(20)知，当u>1时，y为增函数，由式(21)知，当u右趋近1时，y=0，则当u>1时，y>0时，可得：

(22)

令z=0.4u2/(u2-1)，对z求导：

(23)

由式(23)知，当u>1时，函数z为减函数，且当z=1时，u=1.290 994 45，则u∈[1.3,∞)时：

(24)

由上述分析可知，在u∈[1.3,∞)范围内，迭代式(16)对任意u均收敛。

2.4 初值函数的选取及正常水深的直接计算公式

已知u∈[1.3,9.0]，即k∈[0.164 5，7.093 8]，在u的取值范围内，以一定的步长值给定一组数值，将其代入式(15)中，即可求得相应的无量纲综合参数k值。运用MATLAB，采用最小二乘法求解目标函数，对散点(k、u)进行拟合分析，在拟合过程中根据散点图的曲线形状选取合适的用户模型，使得拟合公式相关系数最大，得到无量纲正常水深u的近似计算公式：

u=1.087k0.741 1+0.230 8k1.367+0.995 9

(25)

当断面形状参数a、流量Q、糙率n和坡降i已知的条件下，由式(14)可计算k的值，然后将k值代入式(25)求得初值u0，然后由式(14)、(16)得到正常水深的直接计算公式，即：

(26)

3 公式误差分析及比较

3.1 本文公式误差分析

在工程适用范围内，即u∈[1.3,9.0]，当已知a、Q、n和i时，k可由式(14)求得，真值u可由式(15)相应求得，而在进行误差分析时，在u∈[1.3,9.0]范围内，给出无量纲正常水深u的值，根据式(14)、(15)、(25)、(26)，反求无量纲正常水深和正常水深，对计算值的误差分析采用相对误差来描述，见图2和图3。

图2 初值公式误差分析Fig.2 Relative error analysis of initial value formula

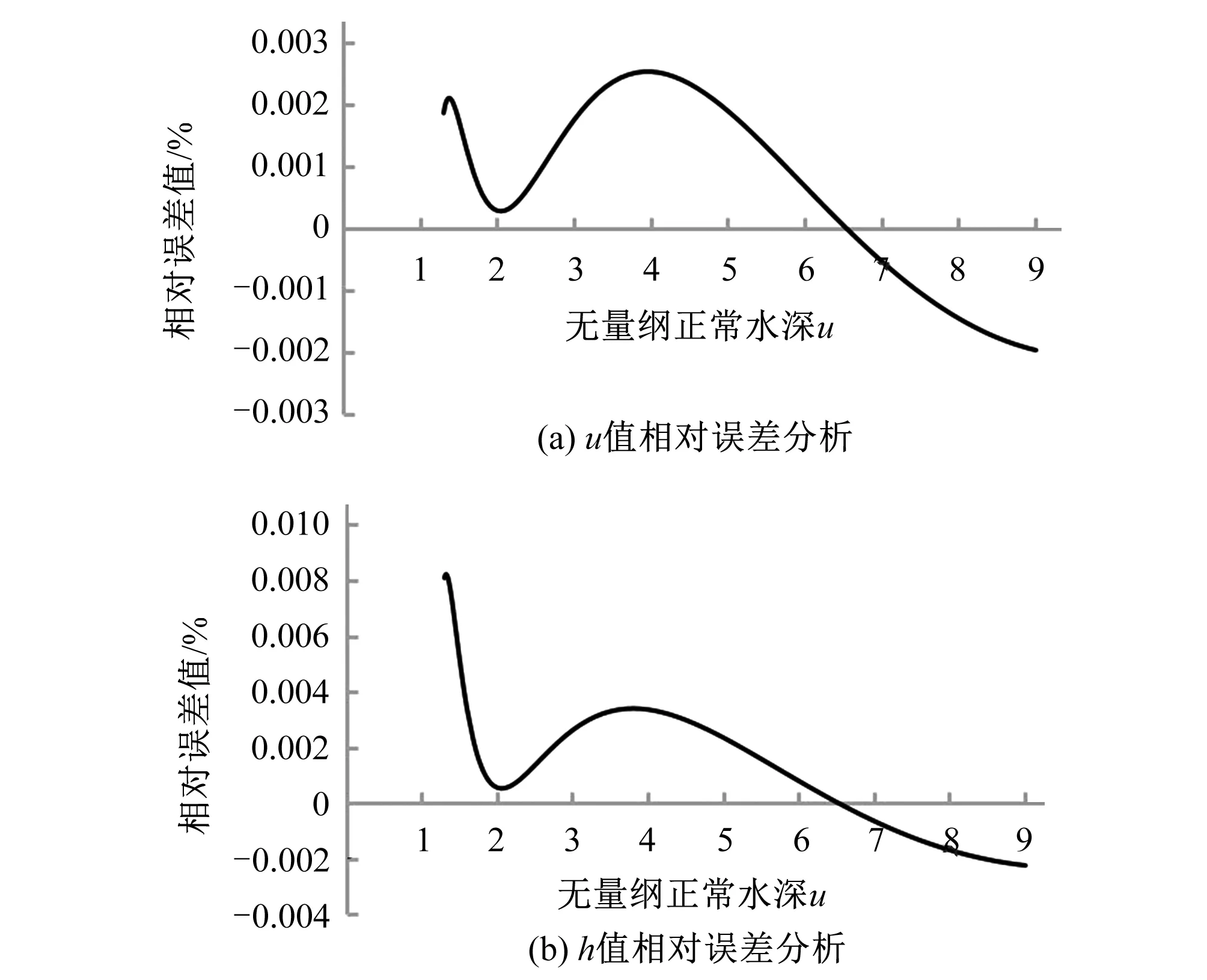
图3 迭代一次公式误差分析Fig.3 Error analysis of the first iteration formula

由图2可见，当无量纲综合参数k∈[0.164 5，7.093 8]时，无量纲正常水深初值最大相对误差的绝对值小于0.014%，正常水深初值的最大计算误差绝对值小于0.054%；迭代一次之后，无量纲正常水深最大相对误差的绝对值小于0.002 6%，正常水深的最大计算误差绝对值小于0.008 3%，可见，本公式为高精度计算公式，完全满足工程需要。

3.2 各家公式对比分析

在目前为止，对于悬链线形断面非设计流量相应正常水深的计算，共有3家公式可供参考，各家公式对比分析情况见表1。

由表1可见，设计流量相应相正常水深的计算值为精确解，而对于非设计流量相应正常水深计算公式，本文初值计算公式精度最高，高于黄开路等[16]公式、滕凯[17]公式和文辉等[18]公式，而迭代一次的直接计算公式精度数量级达到10-3。

4 应用举例

选用文献[21]算例：某渠道横断面的形状为悬链线形, 其设计流量Q=3 m3/s，渠道坡降i=1/1 500，糙率n=0.014，选用η=3.315。

表1 悬链线形断面非设计流量相应正常水深计算公式统计表Tab.1 statistics table of normal water depth calculation formula for undesigned flow rate of catenary-shaped section

注 ：滕凯[17]公式，当u∈[1.3,9.0]时，正常水深h最大相对误差绝对值为0.162%。

在工程设计时，Q为设计流量，本文采用设计流量相应正常水深计算公式，得到解析解，同时采用非设计流量相应正常水深计算公式，计算正常水深，对公式精度进行验证，计算步骤如下：

(1)当已知η、Q、n和i时，由式(12)可得，该渠道正常水深的精确解为h=1.308 82 m。

(2)将η值代入式(11)，可得a=0.762 56 m。

(3)在a、Q、n和i已知的条件下，由式(14)确定k值，k=1.363 1。

(4)将k值代入式(25)，即可得到迭代初值u0=2.716 518，由式(14)可得正常水深h0=1.308 948 m，则相对误差为0.009 78%。

(5)将迭代初值u0代入直接计算公式(26)，得u1=2.716 384，由式(14)可得正常水深h1=1.308 456 m，则相对误差为0.001 96%。

5 结 语

依据悬链线形断面几何特征、水力要素和正常水深基本方程，得到设计流量相应正常水深的解析解公式；通过引入恰当的无量纲参数，对正常水深基本方程进行数学变换，得到正常水深的迭代计算公式，同时利用优化拟合原理得到正常水深的初值计算公式，经一次迭代得到非设计流量相应正常水深的直接计算公式，最后对公式进行误差分析及比较，结果表明，在工程适用范围内，初值计算公式的最大相对误差绝对值小于0.054%，直接计算公式的最大相对误差绝对值小于0.008 3%，远高于现有计算公式精度，且公式结构简捷、适用范围广、物理概念清晰。

□