形象思维在“电路”课程中的培养和应用

2018-12-27赵鑫泰

电气电子教学学报 2018年6期

赵鑫泰

(东南大学信息科学与工程学院，江苏南京 210096)

0 引言

电子信息类专业有五门专业基础课：“电路”、“电子线路”、“信号与系统”、“电磁场”和“电工学”[1]。“电路”课程的重要性由此可见一斑。该课程上承“高等数学”和“大学物理”等通识课程，下启“电子线路”、“信号与系统”等重要的专业基础课和专业课，是理科和工科的“分水岭”，是基础的基础。与其他专业基础课和专业课相比，“电路”课程涉及的概念总体来说并不困难，但由于学生对于有些概念缺乏感性认识，因此理解起来并不容易。此外，由于“电路”课程的基础地位，学生必须对这些概念从感性到理性都有深刻的理解，才能有效地进行本专业的科学研究和生产实践。

目前，“电路”教学普遍存在的问题是：重视理论分析，忽视对基本概念的理解。我们经常会发现，教师在课堂上讲述的基本上都是公式和推导过程，对于公式推导所涉及的物理过程却少有提及。这种教学过程就会造成以下结果：离开了公式，学生对电路问题便一筹莫展。毋庸置疑，定量分析在理工科的教学和科研中都是非常重要的。但是，不能理解公式的物理意义，不能还原数学公式所反映的物理过程，那么，定量计算的作用只能是获得分析结果，对于设计乃至创新则无能为力。而对于理工科人才培养来说后者才是最重要的。

事实上，理工科的任何发明创造都是从定性分析开始的，然后才能进行定量计算。在工程师进行电路设计的时候，经常进行的工作就是调试器件的参数，以使电路性能达到指标要求。要完成这个工作，工程师必须对电路中每个器件的作用有清楚的认识，知道电路的哪些指标主要受哪些器件参数的影响，是如何影响的。这些问题只靠列方程、解方程是很难解决的。解决这些问题需要工程师对电路中发生的物理过程有一定的了解，即工程师能够用形象思维去考虑电路的行为。此外，我们经常会说“站在巨人的肩膀上”，那么怎么样才算是“站在巨人的肩膀上”?欧姆脑子里一定不是只有公式v=iR；法拉第脑子里也一定不是只有公式v=-dφ/dt。这些公式只是他们研究的最终结论，他们脑子里一定还有更多的形象的物理过程。当我们继承前人成果的时候，既需要继承他们得到的结论，更需要继承他们认识到的那些物理过程，只有这样，我们才能再去进行新的更伟大的发明创造。

1 学习迁移理论的应用

在“电路”课程的学习中，有些概念和物理过程是学生在现实生活中有所体验的；而有些则没有，这给理解掌握这些内容带来了很大障碍。这样概念和物理过程需要用学习迁移理论去讲授。

教育心理学家桑代克以刺激——反应的联结理论为基础，提出了学习迁移的相同要素说。他认为只有当两个机能的因素具有相同的要素时，一个机能的提高才会促进另一个机能的提高。也就是说，只有学习的情境和迁移的情境具有共同成分时，一种学习才能对另一种学习产生影响，即产生学习迁移。

为了使学生更好地理解电路中从未亲身经历过的概念和物理过程，教师需要开动脑筋找到合适的概念和物理过程进行学习迁移[2]。

2 电路中重要概念的形象思维培养

前面已经说过，“电路”课程涉及到高等数学的很多内容，但是很多学生对高等数学知识的掌握仅限于机械的计算，对计算的实际含义知之甚少，这种思维方式延续到“电路”学习中，最终的结果也还是只能计算，不清楚所计算的物理过程。因此，笔者在“电路”课程教学实践中首先使学生对高等数学的概念和方法形成形象思维，然后才能使学生对“电路”课程的内容形成形象思维。

下面，笔者就以举例说明的形式，表达如何使学生运用形象思维的过程。

2.1 基本数学概念举例

1) 导数

每个学习过高等数学的学生都知道，一个函数f(t)的导数g(t)可以写成以下形式

(1)

而且知道sin(t)的导数是cos(t)，x2的导数是2x等等。但是导数为何写成这种形式，这种表达方式有何实际意义就不太清楚了。

事实上，字母d是英文differential的首字母，而differential既有微分的意思，又有差分的意思。可见在欧美人的意识里，微分和差分并没有本质的区别。因此，df(t)就是Δf(t)，只不过df(t)是一个非常非常小(专业术语叫无穷小)的增量，Δf(t)是一个有限的增量；同理，dt就是Δt，只不过dt是一个非常非常小的增量，Δt是一个有限的增量。那么df(t)/dt就是在某一个非常非常小的时间段内f(t)的变化率，即瞬时变化率。例如，若f(t)是位移，那么df(t)/dt就是速率。

导数的这种实际意义也可以通过函数的曲线来说明。

如图1所示，Δf(t)/Δt是f(t)在[t1,t2]时间段内的平均变化率。现在使A点与B点非常非常接近，那么Δf(t)/Δt就变成了df(t)/dt，可见df(t)/dt就是f(t)在B点的变化率，也是B点切线的斜率。

图1 导数的实际意义

2) 微分

有了对导数实际意义的理解，对微分的理解就很容易了。

从数学形式上理解，将导数定义式(1)左右两边同乘dt，就得到微分的定义式；

df(t)=g(t)dt

(2)

从实际意义的角度理解，既然g(t)是f(t)的变化率，那么，g(t)dt就是f(t)在dt时间段内的增量。

3) 积分

在微分的基础上建立积分的概念。

(3)

图2 积分的实际意义

4) 微分方程的求解

设有一个微分方程：

f(t)|t=t0=f(t0)

(4)

其中F(t)已知，求f(t)。要求解f(t)，我们已经知道的是f(t)的导数F(t)，即f(t)的变化率，亦即f(t)的每一点的斜率。根据这个已知，我们就可以画出曲线，使它在每一点的斜率都是F(t)，例如，图3中的曲线1，但是具有这种斜率的曲线有无穷多条。那么，哪一条是我们要求的呢？根据初始条件f(t)|(t=t0 )=f(t0)，因此通过点(t0,f(t0))的曲线3就是我们要求的曲线。

如果是二阶方程

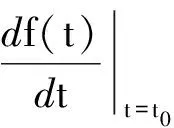
(5)

图3 一阶微分方程的求解过程

那么我们可以将其写成

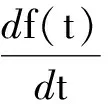
(6a)

(6b)

的形式，这样我们就可以通过求解两个一阶微分方程的方法得到二阶方程式(5)的解。从这里也可以理解，为什么一阶微分方程定解需要一个初始条件；而二阶微分方程定解则需要两个初始条件。

2.2 基本元器件举例

1) 电容

电容的伏安特性是

(7)

其中C、i和v分别是电容、电容电流和电容电压。很多学生只会死记硬背这个公式，考完试就全还给教师了。其实这个公式有明确的物理意义。

(8)

根据电容的定义

Cv=Q

(9)

因此，式(7)实际上就是

(10)

式(10)所反映的物理过程非常直观：电流是电荷的变化率。

如果已知电容电流i，则电容电压

(11)

则是(-∞,t]时间段电容电压的增量；-∞时刻的电压是v(-∞)，因此，t时刻的电压就是式(11)。

其实，式(9)对于学生来说仍然缺乏感性认识，毕竟没有人看到过电荷，更不可能看到它的充放电过程。事实上，电容是电荷的容器，它的很多特性都可以用水杯来比拟。我们把电容C比作水杯的底面积，电压v比作液面高度，电荷Q比作水量，那么，显然电荷量Q等于底面积C乘以液面高度v，就是式(9)[3]。

2) 电感

电感的伏安特性是

(12)

其中L、i和v分别是电感、电感电流和电感电压。这个公式也有明确的物理意义。

(13)

根据电感的定义

Li=φ

(14)

因此，式(14)实际上就是

(15)

式(15)表明电压是磁通量的变化率，也就是法拉第电磁感应定律，只不过此处电压的参考方向与法拉第电磁感应定律中电压的参考方向相反。

如果已知电感电压v，则电感电流

(16)

电感、感生电动势、感生电流对于学生来说是难以体验的。学生脑子里关于磁的感性认识基本上就是磁铁之间的相互作用、法拉第电磁感应和电流的磁效应等宏观的实验。但对感生电动势和感生电流的物理过程很难有所感受和体验。

事实上，我们可以用以下物理过程去理解电磁感应的物理现象。假设山顶上有一个静止的石块，它具有势能；我们推石块使它在山顶上运动起来，则它又具有了动能。假如这个石块完全由电子构成，那么当它静止时，它具有电势能；如果我们“推动”它，使它运动起来，那么这个运动的电子石块又会具有磁能。从以上分析可以看出，电磁学中的电势能与力学中的势能相似，而磁能与力学中的动能类似。电子的动能是否就是磁能这个问题笔者并不知道，但我们确实可以借助这种比拟去理解磁现象。

想象一下我们用手去推电子石块，这个“推动力”就是外加电压；此时，电子石块开始逐渐加速，由于运动的电荷就是电流，(此处的电流不是空间上连续的电流)，因此，电流开始逐渐增加，这个电流就是感生电流 (由于在有限的“推动力”下，电子石块的速度不可能发生突变，也就是说，如果外加电压是有限的，那么，感生电流不可能发生突变)；同时，我们一定会感受到电子石块对我们双手的“反作用力”，这个“反作用力”就是感生电动势；然后，我们不再“推动”电子石块，由于惯性，电子石块不会马上停下来，而是要继续向前运动一段时间，这个运动的电子石块也是感生电流，维持这个电流的电压也是感生电压。

从这一比拟我们可以看到，石块的力学特性和电子石块的电磁学特性非常相似，借助这种比拟，学生可以很好的体会磁现象和电感的特性[3]。

利用前面对电容和电感建立起来的感性认识，我们来分析一下LC振荡电路的工作原理。

2.3 基本功能电路举例——LC电路

LC振荡电路是一个重要的由无源器件构成的基本功能电路，在没有任何外加激励的情况下，电路能够产生持续的电压和电流，这对于初学者来说是一个比较神奇的现象。学生需要对这个电路中的物理过程有详细的了解，才能有效的进行电路设计和调试。

LC振荡电路如图4所示。

图4 LC振荡电路

假设电容上有初始电压vC(0)，电感初始电流为0，则开关闭合后，电容开始放电，电容电压这个“推动力”开始推动回路中的电子逐渐加速，即回路电流逐渐增大，电子会给“推动力”的施加者电容一个“反作用力”，即感生电动势；随着电容电压的减小，回路中电子受到的“推动力”逐渐减小，但电子的速度仍然在增加，只不过速度增加得越来越慢了，也就是“加速度”越来越小了；当电容电压为0时，电子的速度达到最大，回路电流达到最大；此时，尽管“推动力”消失了，由于“惯性”，电子还要继续运动一段时间，也就是感生电流还要持续一段时间，这个感生电流会给电容反向充电，与初始电压反向的电容电压会逐渐增加，电子在其运动方向的反方向受到的“推动”力会越来越大，因此，电子的速度越来越慢，而且速度变慢得越来越快，回路电流越来越小，直至为0；此时电容反向充电完成。如果电路中没有损耗，电容中存储的电能和电容中的初始能量相等。之后，电容再次放电，电感再次充磁……周而复始，形成振荡过程。