时间相关观测的几种动态数据处理方法
2018-12-27李博峰章浙涛
李博峰,章浙涛
同济大学测绘与地理信息学院,上海 200092
在现代大地测量动态数据处理中,只要观测值数量大于未知参数个数,即可建立数学模型并采用逐点单历元的平差方法求得所需的动态解[1-2]。数学模型包括函数模型和随机模型两部分,前者表征的是观测值和未知参数之间的关系,而后者描述的是观测值的精度以及相互之间的关系,两者同等重要且缺一不可[3-4]。
通常,可以认为观测误差为高斯白噪声,即假设观测值之间不存在时间相关性。然而在实际观测数据中,由于非模型化误差的存在[5-6],导致观测值中往往包含具有时间相关性的有色噪声,从而影响了已建立数学模型的正确性[7-10]。事实上,在实际应用中如忽略观测值时间相关性往往会得到不可靠的参数解及其精度[11-13]。文献[14]详细分析了忽略观测值时间相关性得到的参数解精度往往过于乐观且不符合实际。文献[15]指出观测值时间相关性将引起GPS长基线定位结果差异达2 cm,在高精度定位领域如变形监测中不可忽略。文献[16]研究了顾及时间相关性可以获得符合实际的最小可探测粗差,从而帮助用户在质量控制应用中得到更正确的结果。此外,在GNSS应用中,文献[17]证明了当考虑观测值时间相关性时,可以提高模糊度固定的成功率,在单频观测值中尤其明显。
然而,在动态数据处理中,顾及观测值时间相关性的平差方法虽然得到了一定程度的研究[1,18-19],尤其是在GNSS导航领域[20-22],但在统一性和实用性两个问题上尚未完全解决。首先,当前应用最为普遍的是通过时间差分变换方式,将原始相关观测值变换为独立观测值,从而达到消除观测值时间相关性的目的[18,20,23]。事实上,类似的还有去相关变换法,如利用LDLT分解对观测值的方差-协方差阵进行变换[15]。遗憾的是,这些方法的特点以及相互之间的关系目前并没有得到详细论证,因此容易让人产生困惑,造成混乱。其次,由于时间相关观测的动态数据处理中的方差-协方差矩阵不再是一个分块对角矩阵,单历元或者法方程叠加的方法不再适用,直接求逆又会引起巨大的计算量[24],有色噪声模型往往又很难实时准确地获取[25-27],因此在实际应用时,需要有简化的方法在能够保证解算效率的同时又能有效顾及时间相关性。
因此,本文将深入研究几种时间相关观测的动态数据处理方法。首先,对时间相关观测的动态数据处理方法进行了扩展和统一。利用极大验后(MAP)估计原理,提出了顾及观测值时间相关性动态解的第3种思路,并针对无历元公用参数和有历元公用参数两类应用情景,详细推导了去相关变换法、差分变换法和MAP估计法这3种顾及时间相关性的动态解的解析公式,并重点探讨了它们的适用范围以及等价性。其次,导出了一种实用的时间相关观测的动态数据处理方法,即针对严格考虑时间相关性会导致计算复杂且效率低的客观问题,采用自相关函数(ACF)实时估计时间相关性,从而发展了一种简化且能有效表征观测值时间相关性影响的退化形式。最后,采用双频GPS试验数据,对本文理论进行了验证。
1 无历元公用参数的时间相关观测模型
首先探讨无历元公用参数的时间相关观测模型,例如采用GNSS伪距或者模糊度固定后的载波相位进行动态定位。设连续K个历元观测值时间相关,对应的观测方程及其方差-协方差阵为
y=Ax+ε
(1a)
(1b)

1.1 去相关变换法
利用LDLT分解法对方差-协方差阵Qyy进行变换,令分解形式为Qyy=UDUT,其中,U为单位下三角矩阵,对应的递归公式为[28]
(2)
式中,Uij表示单位下三角矩阵的第i行第j列子矩阵;D=blkdiag(D1,D2,…,DK)为分块对角矩阵。令LQyyLT=D,则
(3)
去相关变换法的基本思想是,通过对相关观测值改造,得到一组新的独立观测量。具体的,对观测方程式(1a)左乘矩阵L,得到新的观测方程
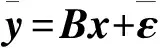
(4a)

(4b)

(5)

(6)
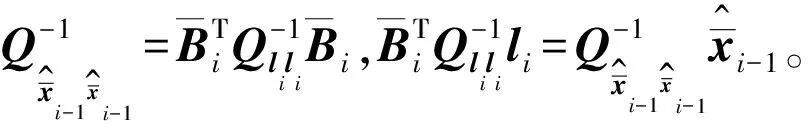
(7)
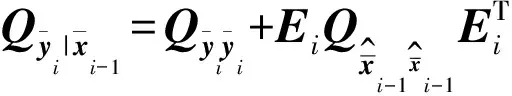
1.2 差分变换法
将观测方程式(1a)按前i-1个历元和第i个历元分块表达,则前i-1个历元的观测方程为
(8)

(9)

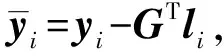
(10)
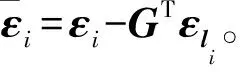
(11)

(12)
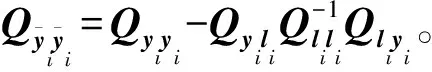
(13)

(14)

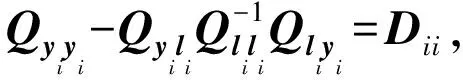
1.3 极大验后估计法

(15)
(16)
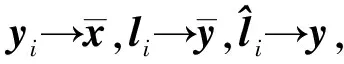
(17a)
(17b)
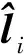
(18)
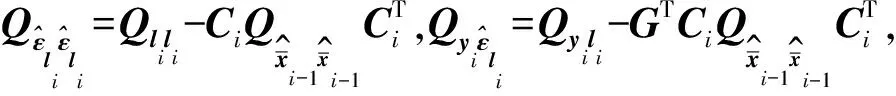
(19)
(20)
(21)
将式(20)和式(21)代入式(18)得式(14),即证明了MAP法与差分变换法的动态解是等价的。类似的,MAP估计法不需要前后历元的观测值类型和维数相同,而差分变换法则需要。
2 有历元公用参数的时间相关观测模型
在某些应用场景下,历元间往往存在公用参数,例如,在GNSS长基线精密定位中,除了随历元变化的位置参数外,还含有未固定的模糊度参数和天顶对流层参数。此时,即使历元间观测值相互独立时,也不能再用单历元观测值单独平差的方法,而需要多个历元联合进行平差。但传统的多历元平差方法因其需要不同历元的观测值,容易引起解算效率低的问题。因此,为了能够保证解算结果不变的情况下,尽最大可能地提高解算效率,本节将探讨有历元公用参数的时间相关观测模型的动态数据处理方法。设连续K个历元的观测值存在时间相关,除了随历元变化的参数x外,历元间还存在公用参数ξ,则K个历元的观测方程为
y=Ax+Cξ+ε
(22)

对观测方程式(22)左乘矩阵L,得到类似于式(4a)的去相关后的观测方程

(23)

(24)
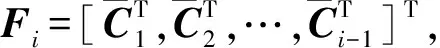
(25)
式中,将式(25)与式(24)的第2个方程进行最小二乘准则下融合,得法方程
(26)
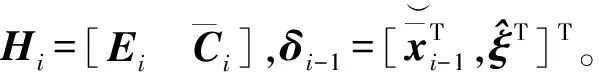
采用最小二乘法方程约化且根据矩阵反演公式,推导得到第i个历元的参数最小二乘估值为
(27)

3 基于ACF的退化形式
虽然上述解算公式严密准确,但涉及大量的矩阵运算,计算复杂且效率低。折中的方法是采用尽量简洁且能有效刻画时间相关性的协方差函数,从而在满足计算效率的同时能符合实际时间相关误差特征。假设各历元观测值的方差-协方差阵相同,利用ACF估计该时间相关系数,且相邻历元的时间相关系数为ρ,则原始方差-协方差阵为
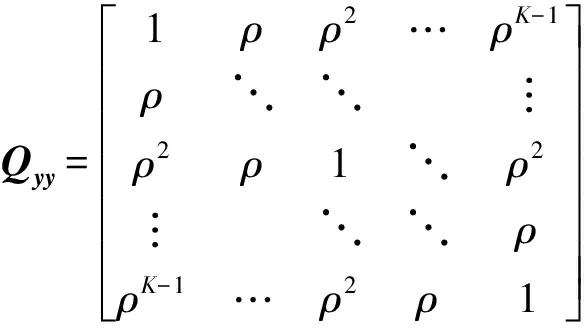
(28)

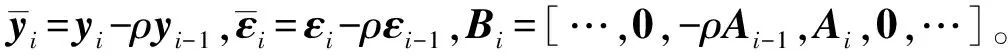
(29)

4 算例与分析
为验证上述理论公式推导的正确性和实用性,选取了同一测区同一时间段内的两条基线长度分别为11.4和42.5 km的双频相位GPS数据,分别命名为No.1和No.2。采样间隔为1 s,时间长度为1 h,模糊度已事先固定。首先利用传统的单历元单独平差方法,获得定位结果,并采用ACF计算观测值残差的时间相关性,通过得到的时间相关系数可以判断相应观测值是否存在时间相关性。图1是两条基线的双频相位观测值时间相关系数,其中每条曲线代表一个双差卫星对。显然,对于这两条基线,时间相关性在一段时间内都是显著存在的。因此,采用顾及观测值时间相关性的动态数据处理方法是必要的。
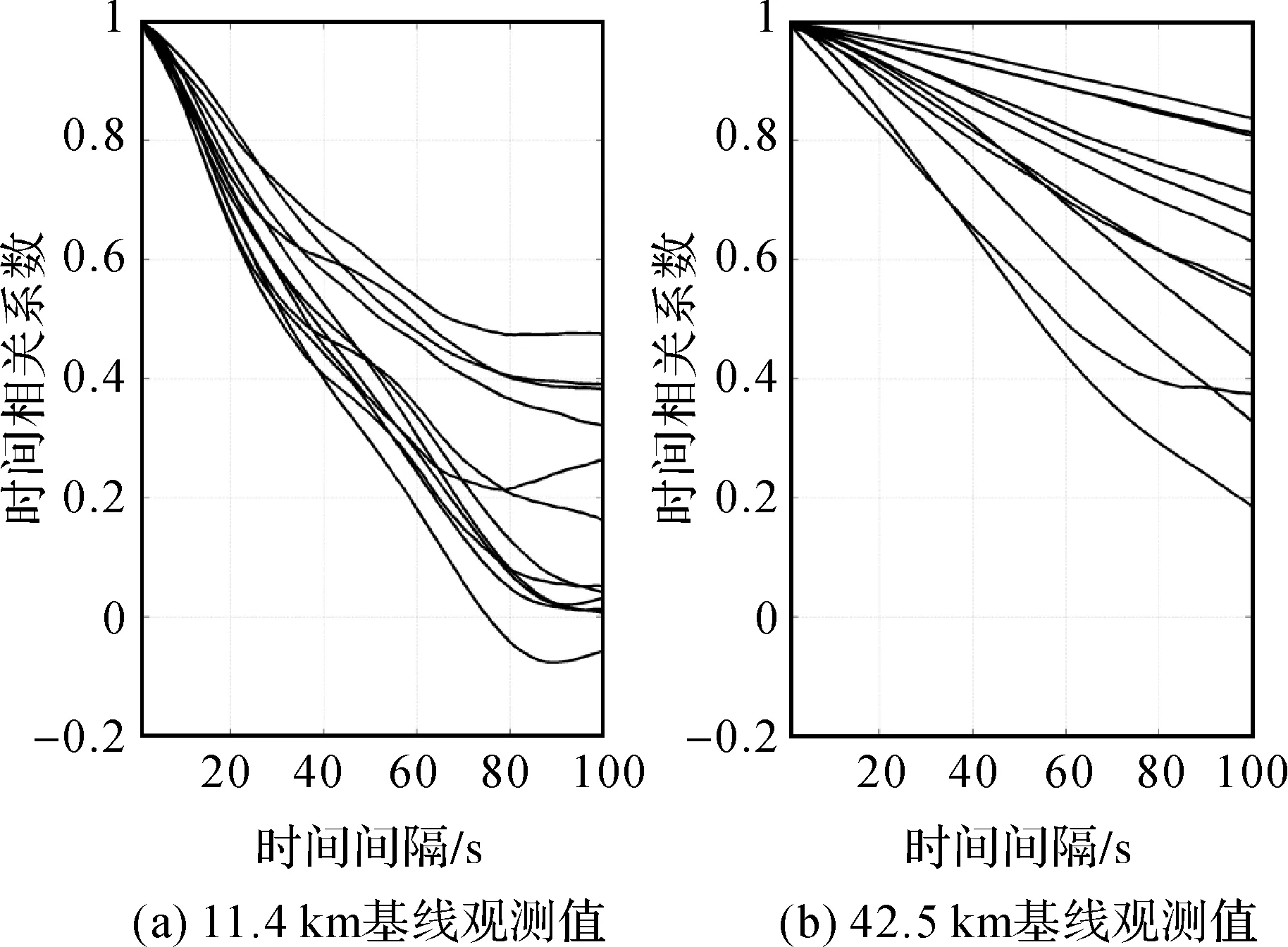
图1 GPS观测值时间相关系数Fig.1 Time correlation coefficients of GPS observations
为分析观测值时间相关性的影响因素,统计了这两条基线所有双频相位观测值时间相关性小于0.3以及接近0时的平均时间间隔,这里0.3和0分别认为时间相关性不显著以及不存在。计算可得,当基线长度为11.4 km时,观测值时间相关性不显著以及不存在的时间间隔平均为86和181 s;而当基线长度变为42.5 km时,相应时间间隔平均为220和396 s。即在200~400 s之后,观测值时间相关性才可以完全忽略。事实上,之所以不同基线长度的观测值可以忽略时间相关性的时间间隔不同,是由于上述时间相关性主要是因为观测值中存在一些难以通过经验模型改正及参数化吸收等的非模型化误差所引起的[5-6,30]。显然,当基线长度越长,所受到的大气误差越严重,因而非模型化误差也越严重,即造成了观测值时间相关性也越强的现象。
接着,采用上述时间相关观测模型中的3种方法分别进行计算,即A、B和C分别表示去相关变换法、差分变换法和MAP估计法。统计了利用这些方法对No.1和No.2这两条基线进行解算后的定位误差的均值和标准差,可以发现这3种方法的定位误差都在厘米级,且他们的定位结果等价,具体统计结果如表1所示。因此,验证了本文公式推导的正确性及3种方法等价性的论断。

表1 两组数据的定位统计结果

下面将以GNSS模糊度固定为例来研究考虑时间相关性的作用。基于LAMBDA方法,分别采用L1、L2和L1+L2进行单历元模糊度固定,并与真值比较分析模糊度固定成功率。以No.1为例,表2显示的是不顾及和顾及时间相关性的模糊度固定成功率。当考虑时间相关性时,模糊度固定的成功率显著提高,平均提高约7%。其原因是考虑时间相关性的方差-协方差阵更加符合实际观测数据情况,导致模糊度搜索空间与浮点解相容[17]。
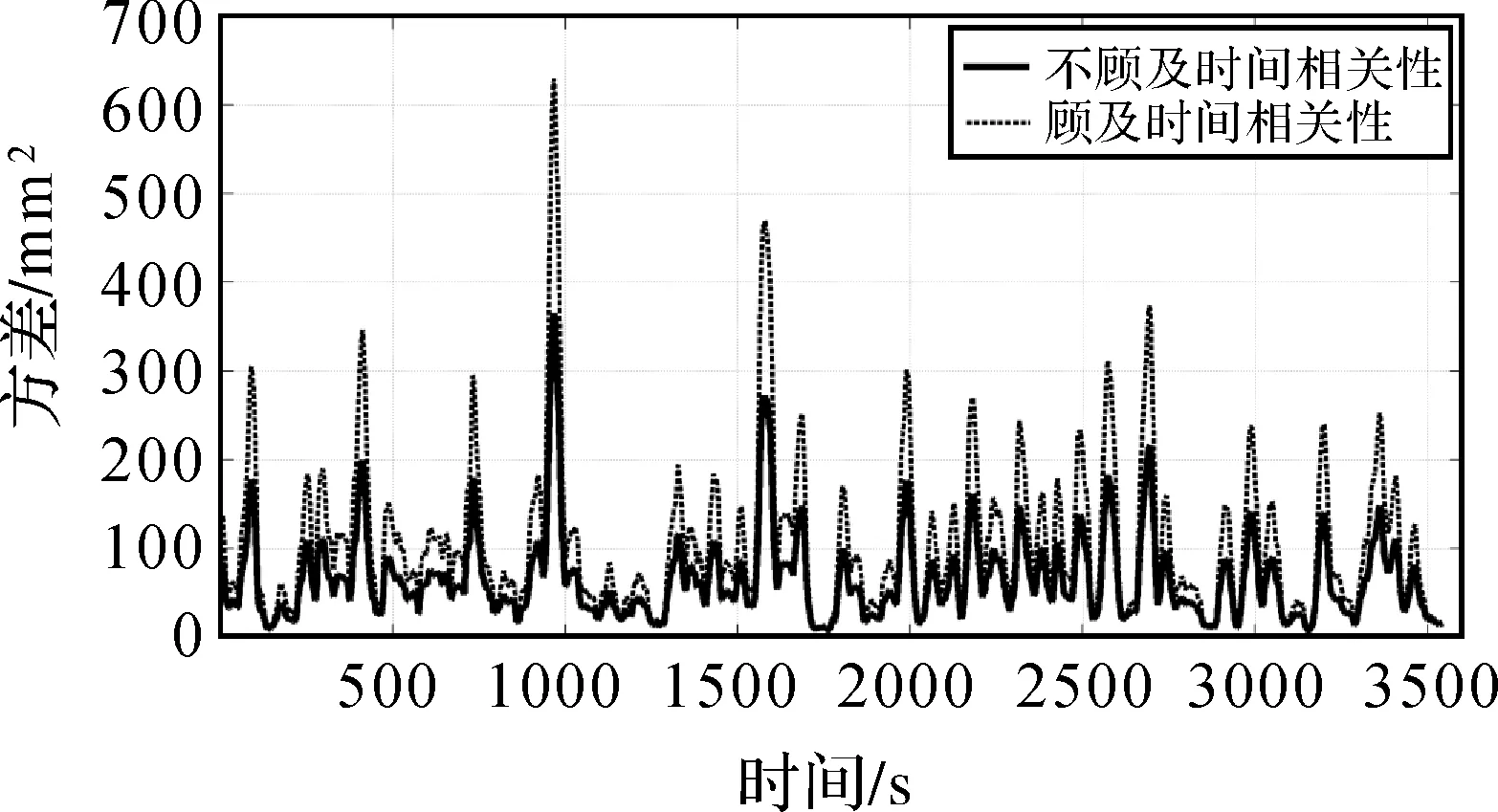
图2 No.1数据U方向上不顾及和顾及时间相关性的定位精度比较Fig.2 Positioning precisions of ignoring and considering time correlations in U direction of dataset No.1
表2No.1数据不顾及和顾及时间相关性的模糊度固定成功率
Tab.2AmbiguityresolutionsuccessratesofignoringandconsideringtimecorrelationsofdatasetNo.1(%)

5 结 论
本文围绕解决现代大地测量数据处理中观测值时间相关的问题,深入研究并提出了几种时间相关观测的动态解法,包括无历元公用参数和有历元公用参数两类模型下3种方法的推导,即去相关变换法、差分变换法和MAP估计法,同时结合ACF,导出了它们的等价退化形式,得出以下结论:
(1) 推导出的3种顾及观测值时间相关性的动态解的结果是等价的且各有特点,因此在实际使用中可选择任意一种易于实现的方法。
(2) 导出的等价退化形式理论上简化了历元之间的关系,且有效提高了计算效率,可以应用于实时观测数据,便于编程计算。
(3) 算例表明,实际观测值中往往存在时间相关性,利用顾及观测值时间相关性的动态解能得到更为可靠和准确的计算结果,如可以提高模糊度固定成功率。
