矩形筒螺栓联结损伤的振动特性研究①

2018-12-27，，

佳木斯大学学报（自然科学版） 2018年6期

，，

(绥化学院农业与水利工程学院，黑龙江绥化 152000)

0 引言

工程结构由于环境荷载、疲劳效应、材料性能退化及其它意外因素都会造成损伤的累积和结构性能的退化，进而发生破坏[1]。因螺栓本身腐蚀以及强度不够引起的受损、疲劳、零件脱落是螺栓结构联接失效的主要原因，而肇事螺栓联接区域往往是螺栓连接结构日常维护的盲点，因此要引起足够的重视[2]。

对螺栓联接部分的有限元建模、预紧力施加成为最近的研究重点。近些年来，许多学者对其进行了大量的研究工作，提出了多种螺栓联接结构的等效力学模型[3]。采用振动的力学方法，并结合有限元分析软件Ansys对工程中常用的矩形筒螺栓联接部件进行有限元模拟，从螺栓预紧力、外载荷以及螺栓联结数量三个方面对工程实际结构的矩形筒进行分析，最后分别总结出以上三种因素对矩形筒振动特性的影响规律。

1 螺栓联结部件模态实验基本理论

1.1 模态分析基本理论

频率与模态都是振动系统自身的固有属性，它们是由系统振动微分方程组的特征值与特征向量组成的[4]。研究系统的振动特性首先要建立结构的物理参数模型，研究其特征值问题，求得系统的特征值与特征向量，得到结构的模态参数模型，包括模态频率、模态矢量、模态质量、模态阻尼、模态阻尼比、模态刚度等参数，进行正则化和解耦过程。最后通过研究受迫动力响应的问题，得到系统的非参数模型包括频响函数和脉冲响应函数，频响函数和脉冲响应函数就是实验模态分析系统识别模态参数的基础。

根据振型关于质量阵[M]与刚度阵[K]的正交性，用各阶模态缩减，考虑比例阻尼系统，引入模态阻尼Cr，对第r阶模态进行解耦，得到全局坐标下的频响函数[5]。

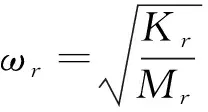
根据上述公式，频响函数矩阵中的各个元素都包含了模态参数Kr、Mr、Cr、ωr、ζr，对于振型的识别，需要矩阵一行或一列的元素。通过锤击法在各个测点进行激励，即可在某点拾取任意一行的频响函数，从而获得部件各阶模态[6]。

1.2 预紧力与预紧力矩的转换

(1)预紧力与预紧力矩的理论公式

螺栓在预紧力矩T的作用下产生预紧力F，螺栓预紧力矩T为：

T=T1+T2

上式中，螺杆与螺母之间的摩擦阻力矩为：

T1=Fd2tan(ψ+ρ′)/2

螺母与联接件接触面之间的摩擦阻力矩为：

T2=μnFrn

d2为螺纹中径，ψ为螺纹升角，ρ′为螺纹的当量的摩擦角。对于大多数的螺纹，螺纹升角ψ是小量，因而tan(ψ)和tan(ρ′)通常也是小量，可得：

tan(ψ+ρ′)≈tan(ψ)+tan(ρ′)

预紧力与预紧力矩在屈服极限之前的关系：

T=Fd2(tan(ψ)+tan(ρ′))/2+μnFrn

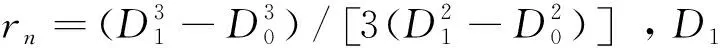
通过公式可以得出，预紧力和预紧力矩呈线性关系，但是如果没有正确的施加预紧力，也可能会出现非线性关系。达到屈服极限后，预紧力的增速减缓，二者的关系曲线出现下弯的情况。

(2)预紧力与预紧力矩的近似式

在工程上，对参数进行了许多近似的估计，螺纹升角ψ=1°42′-3°2′；螺纹中径d2≈0.9d；ρ′=arctg1.155μ(μ为摩擦系数，没有润滑时μ≈0.1-0.2)；螺栓孔直径D0≈1.1d；螺母环形支撑面的外径D1≈1.5d；紧固面之间的摩擦系数μn≈0.15；预紧力与预紧力矩的近似式：

T≈0.2Fd

利用上式可对试验中施加的预紧力矩进行换算为预紧力在有限元的数值模拟中进行施加，进一步保证试验与数值模拟的吻合。

2 矩形筒螺栓联结损伤的振动分析

2.1 有限元模型的建立

矩形筒的有限元仿真计算模型将采用Hypermesh进行实体建模、接触管理和网格划分，后期预紧力的施加、边界条件和外载荷的施加、静力计算以及模态计算将在Ansys中实现[7]。

在单元选取中，筒体选取Solid185八节点六面体单元，螺栓的接触选择接触单元Contact174单元，螺栓的预紧力单元选择Prets179单元，共60204个单元90853个节点。采用一端固定一端自由的边界条件，在自由端施加水平方向的外载荷，载荷模拟后期的工装条件施加在侧边中点处。由于Hypermesh网格划分后导入Ansys只保留了节点，因此外载荷的施加采用分布在节点上的方法，为了尽可能的避免应力集中的现象，将外载荷分别施加在中部10个节点上，来模拟水平方向的外载荷[8]。矩形筒整体以及单个螺栓的有限元模型如图1所示。

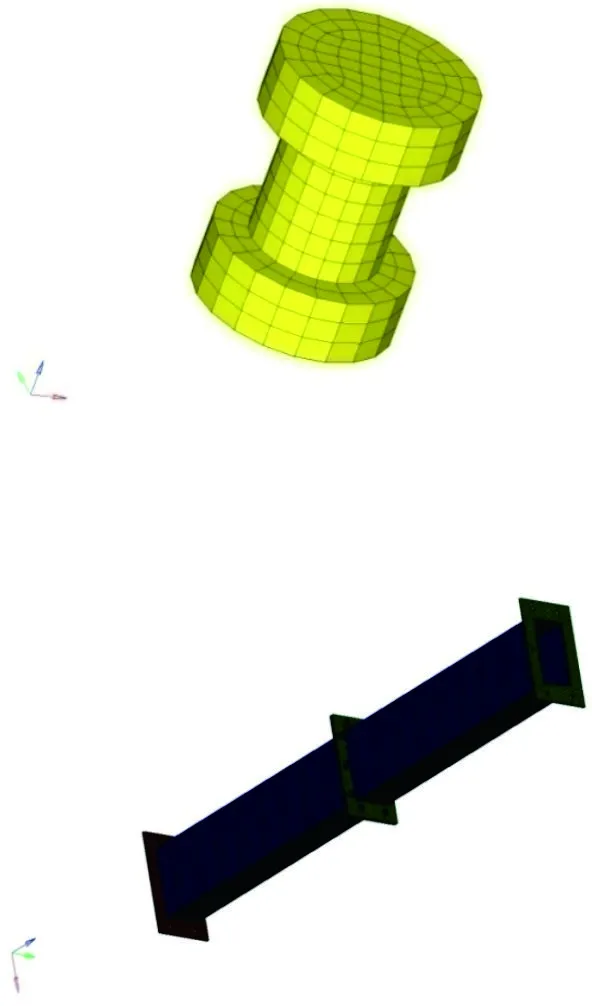
图1 矩形筒的螺栓模型及整体模型

2.2 矩形筒的有限元分析

从螺栓数量、外载荷以及预紧力三个方面出发，采用控制变量法，进行横向对比，之后改变外部条件再进行纵向对比。首先进行螺栓预紧力加载和自由端横向加载的静力分析，然后将静力分析的结果作为预应力效果进行模态分析，得到结构整体的动力学响应参数，最后进行对比分析，总结规律。为了节约时间成本和提高计算效率，本节的模态有限元分析只以结构的第一阶固有频率为基准。

(1)控制螺栓数量保持不变，设定螺栓数量为六个，在此基础上改变螺栓预紧力和外载荷的大小，分别得到不同螺栓预紧力和外载荷作用下矩形筒的第一阶固有频率，如表1所示。

表1不同外载荷和预紧力作用下矩形筒固有频率(Hz)

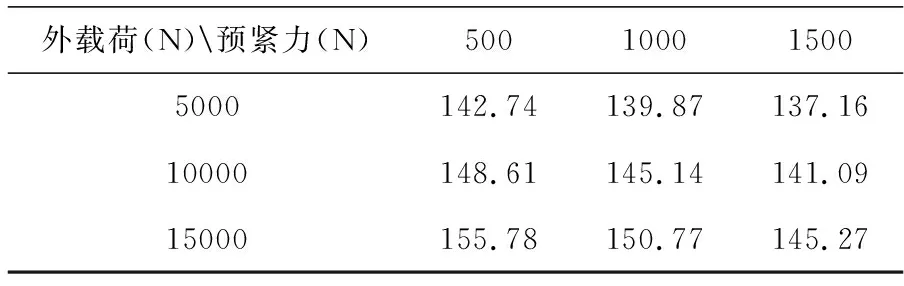
外载荷(N)预紧力(N)500100015005000142.74139.87137.1610000148.61145.14141.0915000155.78150.77145.27

为了更直观的表现出不同螺栓预紧力和外载荷对矩形筒的第一阶固有频率的影响，根据上表的数据绘制出矩形筒第一阶固有频率随螺栓预紧力和外载荷变化图，如图2所示。

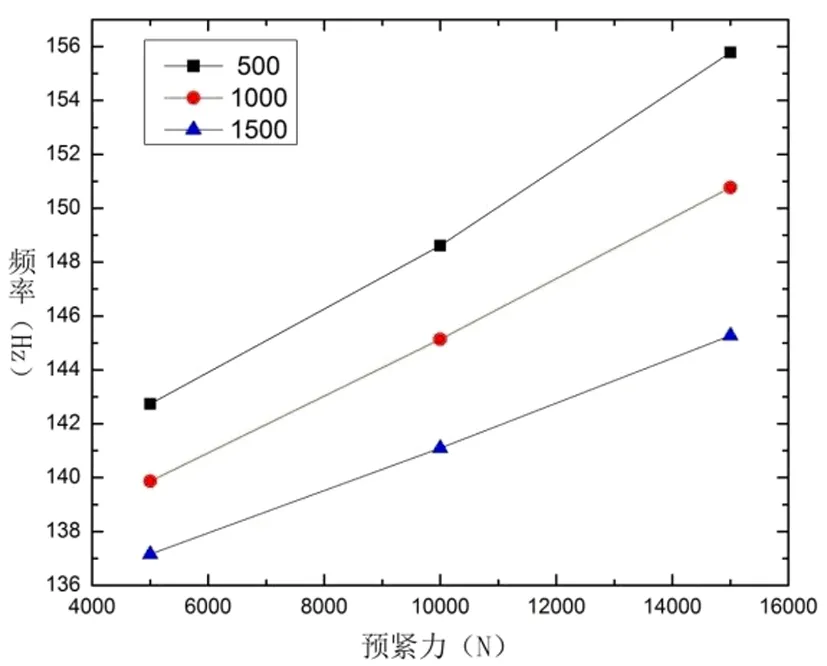
图2 矩形筒固有频率随螺栓外载荷和预紧力变化曲线

从图2可知，在六个螺栓的工装条件下，矩形筒的固有频率随着螺栓预紧力的增大而增大，并且大致成线性变化，当外载荷为500N时，预紧力从5000N增加到15000N导致矩形筒固有频率增加了8.37%，当外载荷为1500N时，预紧力从5000N增加到15000N导致矩形筒固有频率增加了5.58%，这表明当外载荷越大时，螺栓预紧力的改变对矩形筒的固有频率的影响越不明显。

矩形筒的固有频率随着外载荷的增大而减小，当螺栓预紧力为5000N时，外载荷从500N增加到1500N导致矩形筒固有频率减少了3.90%，当螺栓预紧力为15000N时，外载荷从500N增加到1500N导致矩形筒固有频率减少了6.75%，这表明当螺栓预紧力越大时，外载荷的改变对矩形筒的固有频率的影响越明显。

(2)控制外载荷不变，设定外载荷大小为1000N，在此基础上改变螺栓预紧力的大小和螺栓数量，得到不同螺栓数量和螺栓预紧力作用下矩形筒的第一阶固有频率，如表2所示。

表2不同螺栓数量和预紧力作用下矩形筒固有频(Hz)

为了更直观的表现出不同螺栓预紧力和螺栓联结数量对矩形筒的第一阶固有频率的影响，根据上表的数据绘制出矩形筒第一阶固有频率随螺栓预紧力和螺栓数量变化图，如图3所示。

从图3可以看出，在外载荷保持1000N不变的条件下，矩形筒的固有频率随着螺栓预紧力的增大而增大，当螺栓联结数量为2个时，预紧力从5000N增加到15000N导致矩形筒固有频率增加了3.95%，当螺栓联结数量为10个时，预紧力从5000N增加到15000N导致矩形筒固有频率增加了8.37%，这表明当螺栓联结数量越多时，预紧力的改变对矩形筒的固有频率的影响越明显。

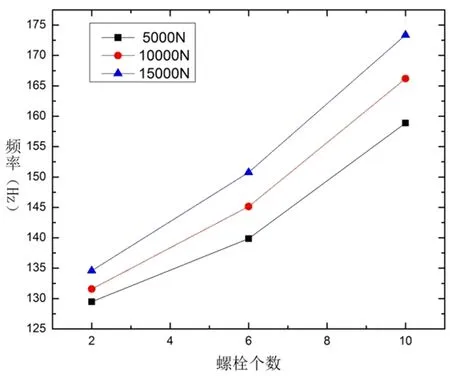
图3 矩形筒固有频率随螺栓数量和预紧力变化曲线

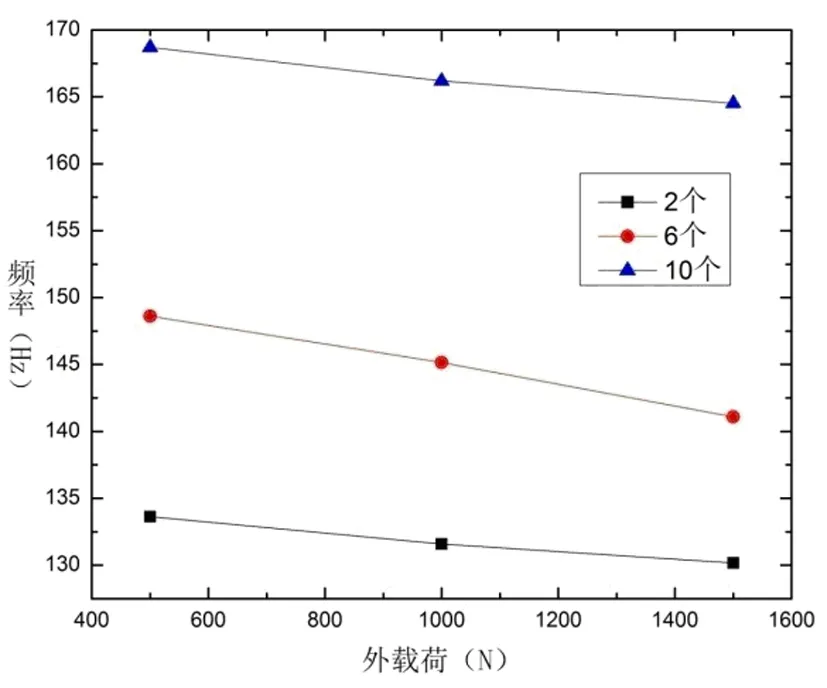
图4 矩形筒固有频率随螺栓数量和外载荷的变化曲线

在外载荷保持1000N不变的条件下，矩形筒的固有频率随着螺栓数量的增多而增大，当预紧力为5000N时，螺栓数量从2个增加到10个导致矩形筒固有频率增加了18.5%，当预紧力为15000N时，螺栓数量从2个增加到10个导致矩形筒固有频率增加了22.4%，这表明当预紧力越大时，螺栓数量的改变对矩形筒的固有频率的影响越明显，并且变化量超过20%，这对矩形筒结构的振动特性已经产生了很大的影响，是工程实际监测中应该优先考虑的地方。

(3)控制螺栓联结的预紧力保持不变，设定预紧力大小为10000N，在此基础上改变外载荷的大小和螺栓数量，分别得到不同螺栓数量和外载荷作用下矩形筒的第一阶固有频率，如表3所示。

表3不同螺栓数量和外载荷作用下矩形筒固有频率(Hz)

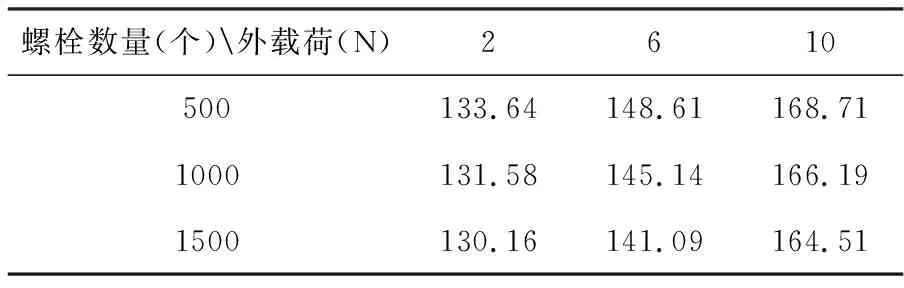
螺栓数量(个)外载荷(N)2610500133.64148.61168.711000131.58145.14166.191500130.16141.09164.51

为了更直观的表现出外载荷的大小和螺栓联结数量对矩形筒的第一阶固有频率的影响，根据上表的数据绘制出矩形筒第一阶固有频率随外载荷和螺栓数量变化图，如图4所示。

从图4可以看出，在预紧力保持10000N不变的条件下，矩形筒的固有频率随着外载荷的增大而减小，当螺栓联结数量为2个时，外载荷从500N增加到1500N导致矩形筒固有频率减小了2.60%，当螺栓联结数量为10个时，外载荷从500N增加到1500N导致矩形筒固有频率减小了2.49%，这表明当螺栓联结数量和螺栓预紧力保持不变时，外载荷的大小对矩形筒固有频率的影响是比较小的，与上文所得到的结论一致。

在预紧力保持10000N不变的条件下，矩形筒的固有频率随着螺栓数量的增多而增大，当外载荷为500N时，螺栓数量从2个增加到10个导致矩形筒固有频率增加了20.8%，当外载荷为1500N时，螺栓数量从2个增加到10个导致矩形筒固有频率增加了20.9%，这表明螺栓数量的改变对矩形筒的固有频率的影响很大，变化量也超过20%，与上文的研究是相符的，在工程实际中应重点考虑。