基于小波变换的陶瓷零件研磨后的正废品识别①

,

(山西机电职业技术学院信息工程系，山西 长治 046011)

0 引 言

绝大多数的工业零件及部件的质量检测已经有了一整套的检测方法和相应的检测设备。但是，还有一些工业零件及部件还没有相应的检测设备，主要靠大量的人力来完成检测。这些工业零件及部件主要有如下特点：结构简单、质量和体积非常的小、造价非常的低廉、但是使用量却非常的大。这些工业零件及部件有个共同的特征就是检测方法非常简单，就是检查零件的表面是否平整，如果零件的表面是平整的就为合格品，否则就为废品。该陶瓷零件认定为废品无非存在三种情况，第一种情况陶瓷零件表面出现划痕、第二种情况陶瓷零件表面存在小孔、第三种情况陶瓷零件表面边缘出现缺口。通常是利用大量的人力进行检查，消耗了大量的人力资源和时间。如果不进行检测，那么采购方采购回去也要进行检测，如果废品率超过一定量，那么供货方就会对采购方给予惩罚性赔偿。所以检测的环节必不可少。所以提出了一种自动检测方法，采用了小波变换后的低频部分做为特征向量，然后采用距离比较的方法进行识别检测。

1 小波变换理论[12]

小波变换是在1988年被提出的，同时还提出了正交小波基和多分辨率的概念，并且给出了快速算法。小波变换也被称为是小波函数，该函数不仅能将信息在频域上处理，也能将信息在空域上处理，其生成的结果大致可以分为低频部分和高频部分，从而达到删除信息中冗余的脏信息，保留重要的特征信息，所以该函数必须具备在其定义域的取值范围内，其所对应的所有的值做平均计算，结果为零，其图像即不对称也不规则，振幅也随时可以发生变化，但是如果是正余弦波就不存在这种情况，波形是稳定的，其振幅也是稳定不变的。所以，小波从提出开始，就已经达到了传统的傅里叶变化的地位，甚至在一些研究领域取代了传统的傅里叶变化。

Haar小波是一种非常特殊的小波变换，结构非常简单，具有很好的正交性和对称性。其函数表达式为：

(1)

Daubechies小波变换也被称作Daubechies N小波变换，该小波变换是在小波变换的基础上进行研究而得到的，通常简记为DbN，其中N表示阶。没有固定的函数表达式，但是具有明显的特点：小波变换在是时间区域上具有一定的支撑，这种支撑是非常有限的； 小波变换在频率范围内，其函数在N值上具有零点。

2 基于小波变换的陶瓷零件研磨后的正废品识别

2.1 图像预处理[34]

通常无论是在识别研究还是在检索研究中，图像预处理是必不可少的阶段，其作用是让识别或者检索的结果达到最佳效果。预处理比较简单，因为陶瓷零件的采集是利用固定高清采集设备垂直拍摄采集，采集得到的照片只有陶瓷零件(图像1)。然后在公式的作用下

g=0.3R+0.59G+0.11B

(2)

完成陶瓷零件的灰度化处理。g为最后生成图像的灰度值，R为图像中红色分量值，G为图像中绿色分量值，B为图像中蓝色分量值(图像2)。

图1 图2

2.2 陶瓷零件特征提取

用小波变换做图像的特征提取，是非常实用的，小波变换是将图像先在水平方向上进行一次处理，然后在垂直方向上进行一次处理，处理结果是将原图一分为四，即缩小了四分之一倍，分别记为LL1、LH1、HL1、HH1(图像3)。LL1图像通常可以作为特征向量来使用，因为该图像是小波变换删除了大量的冗余信息后生产的图像，也叫做近似分量；LH1图像是小波变换在水平方向上进行处理所得到的图像，也叫做水平分量；HL1图像是小波变换在垂直方向上进行处理所得到的图像，也叫做垂直分量；HH1该部分通常不用，但是如果原图像具有丰富的纹理信息时，这部分图像将可以做为特征向量使用，也叫做对角细节分量。这是经过一次小波变换后的结果，如果要再做一次小波变换，可以选取第一次生成的LL1图像，进行一次小波变换，处理结果是将LL1图像一分为四，即又缩小了四分之一倍，分别记为LL2、LH2、HL2、HH2(图像4)。这是经过二次小波变换后的结果，如果要再做一次小波变换，可以选取第二次生成的LL2图像，进行一次小波变换，处理结果是将LL2图像一分为四，即再次缩小了四分之一倍，分别记为LL3、LH3、HL3、HH3(图像5)。这样就完成了三次小波变换，以此类推就可以完成多次小波变换。提取两次小波变换后的LL2图像做为特征向量。

用E来表示陶瓷零件图像，并进行灰度化处理。按照如下方法提取特征：

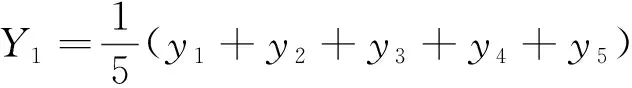
那么向量Y1就为合格品的陶瓷零件的特征向量。

(2)、按照上述方法，提取出不合格的陶瓷零件的特征向量。但是不合格的陶瓷零件有三种不合格情况，分别为：陶瓷零件表面出现划痕、陶瓷零件表面存在小孔、陶瓷零件表面边缘出现缺口。为了能达到比较好的识别效果，分别提取出这三种情况的特征向量，记为：Y2，Y3，Y4。

那么最后由Y1，Y2，Y3，Y4共同组成了陶瓷零件用于识别的特征向量。

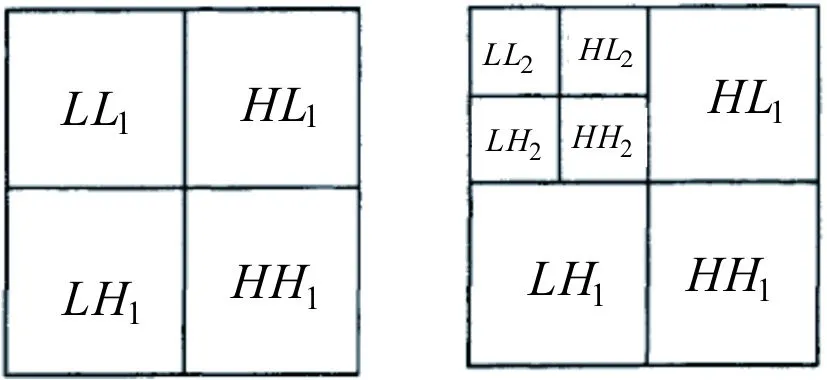
图3 图4

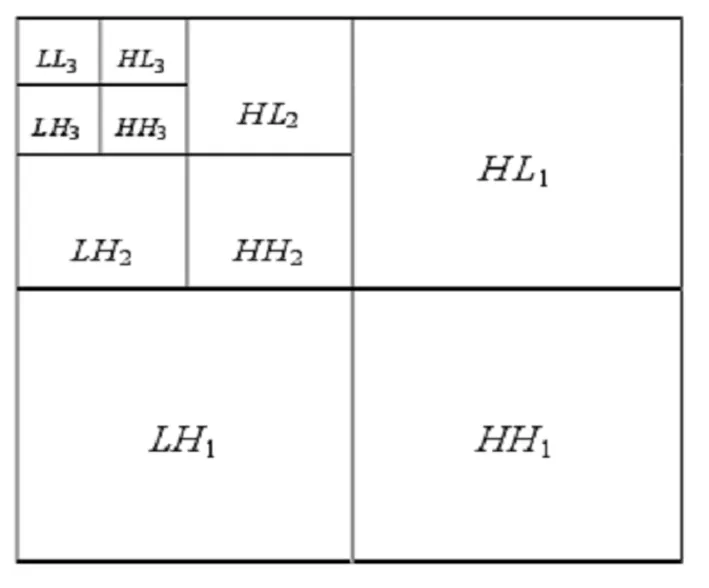
图5

2.3 陶瓷零件识别

识别是在特征提取的基础上完成的，采用比较欧式距离的方式进行识别，也叫做近邻方法[5]。具体识别方法如下：

(1)、准备好待分类的陶瓷零件图像，按照上述方法进行预处理，并在小波变换的作用下，提取LL2图像，并将其转换为行向量的形式，记为：y。

(2)、分别计算特征向量y与特征向量Y1，Y2，Y3，Y4之间的距离，即Li=‖y-Yi‖ i∈(1,2,3,4)

(3)、选取Li中最小的值。如果i=1时最小，那么该用于识别的陶瓷零件图像是合格品，否则为不合格，且i=2时是表面出现划痕不合格品、i=3时是表面存在小孔不合格品、i=4时是表面边缘出现缺口不合格品。

3 实验结果与分析

用于实验的陶瓷零件图像是自己建立的，最终要于实践。为了完成实验，共使用了400张陶瓷零件图像，其中合格品100张，表面出现划痕不合格品100张、表面存在小孔不合格品100张、表面边缘出现缺口不合格品100张。其中各选取5张用做训练，剩下的380张用做识别。实验分析如下：

3.1 多种小波实验分析

小波变换有很多种类，实验只选择了常用的几种小波变换，主要使用了haar小波变换、Daubechies 小波变换，SymletN小波变换，CoifletN变换，其中N取值都为常用的2，利用两次小波变换中的 部分做为特征向量。分别在上述的图像库中进行识别实验，实验分析如下，见表一。

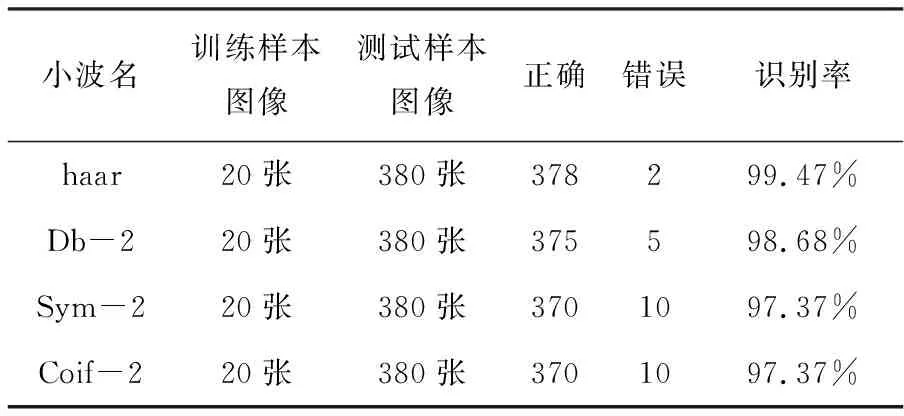
表1 使用不同小波变换

3.2 一次小波变换、二次小波变换和三次小波变换的比较

实验选择都在haar小波上进行，但是特征分别是利用一次小波变换、二次小波变换和三次小波变换中的 部分做为特征向量，分别在上述的图像库中进行识别实验，实验分析如下，见表2。

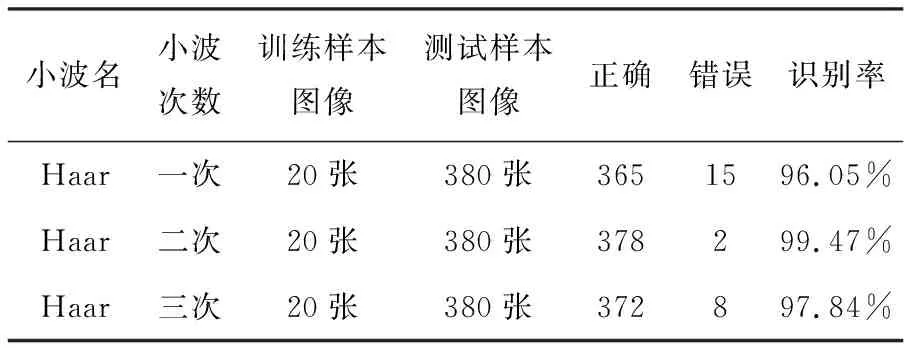
表2 同一小波，不同次数

通过上面两个实验发现，利用小波变换做特征提取进行识别还是非常要有效的，并且发现haar小波的识别效果略高于其他小波变换，同时发现，小波变换的次数对识别效果的影响也是非常明显的，小波变换使用次数越多，删除无用的信息越多，一定程度上会提高识别效果，但是如果小波变换使用次数过多，也会删除某些非常重要的有用信息，反而会降低识别效果。所以，选择适当的小波变换的使用次数，对于识别是非常重要得。

4 结 语

主要研究的一种工业小零件或者小部件的正废品的检测，采用两次小波变换提取特征向量，采用距离比较的方法识别。通过实验验证，该方法在陶瓷零件的正废品自动识别还是有效可行的。仅研究的一部分，下一步要研究如何实现，即考虑采用单片机或者嵌入式使用该算法，应用到工厂的生产实践中。