斜坡地基上高填方挡墙侧向极限土压力简化算法

周应兵，谢 鑫，郭 瑞，刘大伟，肖世国

(1. 中铁十二局集团有限公司衢宁铁路(福建段)Ⅲ标工程指挥部，福建 宁德 352300；2. 西南交通大学地质工程系，四川 成都 610031；3. 西南交通大学高速铁路线路工程教育部重点实验室，四川 成都 610031)

0 引言

斜坡地基上的高填方存在失稳滑动的安全隐患，重力式挡墙是山区道路工程中保持此类填方边坡稳定而常用的一种工程措施。在这种地形条件下，填方产生的作用于挡墙上土压力的问题，不同于水平地面的情况。因受到斜坡面地基边界条件限制，经典的朗肯或库伦土压力理论[1]不一定适用(尤其当斜坡坡度较大时)。针对斜坡地基上高填方挡墙土压力问题，一些学者曾采用试验和数值模拟手段探讨过该土压力分布特征及相关的分析方法[2-5]。李阳等[6]通过对挡土墙与填方土体的相互作用分析，指出了高填方挡土墙破坏机理。王莘晴[7]对桩承扶壁式挡墙在高填方边坡防护工程中的应用进行了研究，通过受力分析建立了桩墙受力模型，给出了桩承扶壁式挡墙的设计方法。范瑛等[8]通过对高填方路基挡土墙现场试验数据进行分析，得到多级重力式挡土墙土压力分布规律。FRIEDLI等[9]采用塑性极限分析方法建立了滑动土体的受力分析模型，推导出墙后土压力的计算方法。邹京成[10]采用极限平衡方法和数值模拟方法，对墙体平动与转动位移模式下的填方挡土墙后土压力问题进行了讨论。谢涛等[11]对贵广高速铁路某陡坡地基路肩桩板墙结构，通过现场实测得到了土压力的分布模式。廖来兴[12]采用数值模拟与现场监测方法，获得了斜坡地带桩承扶壁式挡土墙上土压力的分布模式。张玉伟[13]基于库伦土压力理论，给出了斜陡边坡前缘挡墙主动土压力的近似简化算法。董捷等[14]针对斜坡填方的柔性板桩板墙结构，通过模型试验方法得到了桩前、桩后施工挡土板时墙后土压力的分布特征。

以往的相关研究多集中于挡土墙的破坏机理和土压力分布规律，而针对斜坡高填方挡土墙后土体可能出现的越顶(越过墙顶)失稳模式，及在此情况下作用于挡土墙上土压力计算方法的研究甚少。本文主要针对斜坡地基上填方边坡，基于墙后填土越顶失稳破坏模式，采用极限平衡法分析作用于重力式挡土墙上的侧向极限土压力，推导出相应的计算公式，为实际工程设计提供参考。

1 土压力计算公式推导

斜坡地基上填方作用于挡土墙上的土压力问题可简化为平面应变问题，计算模型如图1所示。墙背BD倾斜，与竖直方向的夹角为ε；假设无黏性填土的填方斜坡面BC为平面，与水平方向的夹角为δ；原自然坡面AD为平面，其与水平方向夹角为α。填土在自重作用下，有向下和向坡体外方向的滑动趋势，假定墙体保持稳定(设计基本要求)，则填方土体极有可能发生图1所示的越过墙顶滑动的“越顶”破坏模式。设在该状态下，潜在滑面AC与自然坡面AD夹角为ω，滑面AB与AD夹角为β。根据各滑块间的相对运动趋势，通过分析可知，滑块ABC的受力均如图2所示。图中T为上部土体作用在滑块ABC上的力，G1为滑块ABC的重力，R为滑块ABD对滑块ABC的反力。

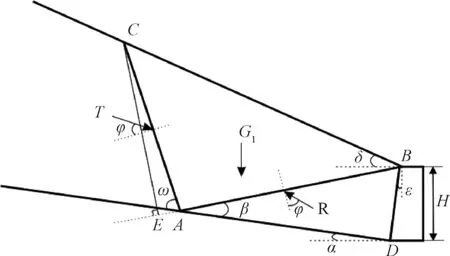
图1 填方土体受力简图Fig.1 Stress diagram of filled soil

根据几何关系有：

(1)

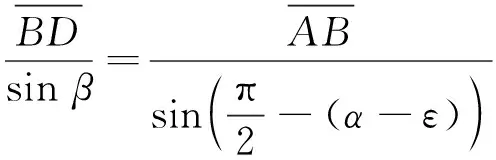
(2)

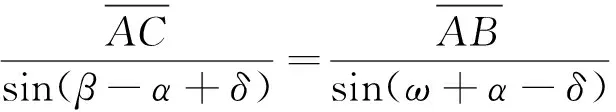
(3)

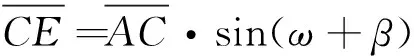
(4)

由式(1)～(4)得到滑块ABC的重力：

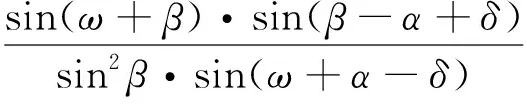
(5)

式中:H——挡土墙墙高;

ε——墙背与竖直线间的夹角，墙背俯斜时为正;

ω、β——墙后填土的破裂角;

α——自然斜坡面倾角;

γ——墙后填土的重度。

考虑滑块ABC的静力平衡条件，由图2可知，G、R与T三个力组成封闭的力的三角形，由正弦定理得：

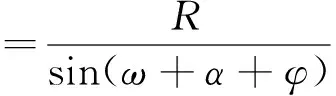
(6)

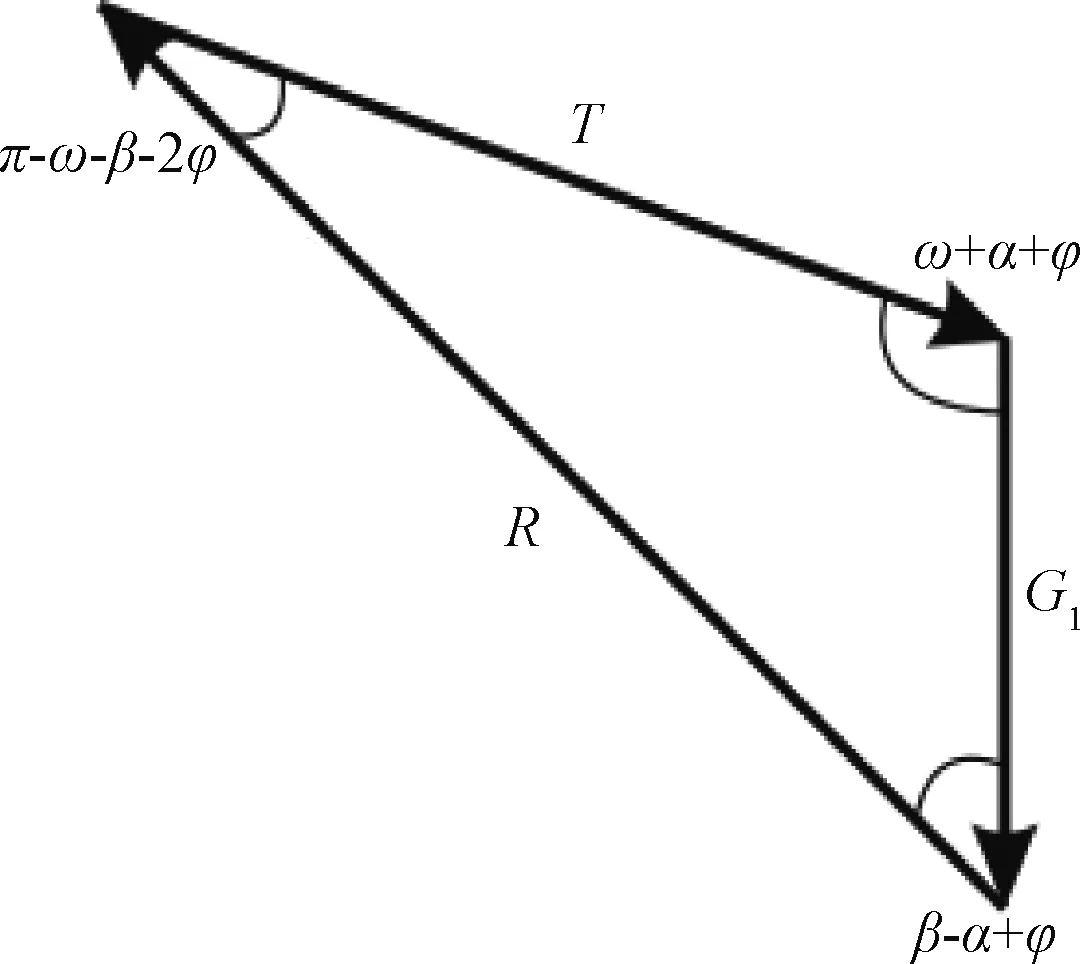
图2 滑块ABC受力分析Fig.2 Force analysis of sliding block ABC

式中φ——墙后填土内摩擦角。

由式(5)(6)得到：

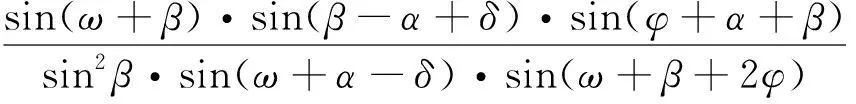
(7)

再由几何关系：

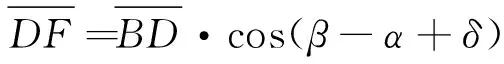
(8)

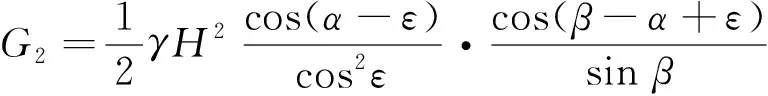
(9)

忽略黏聚力和孔隙水压力，滑块ABD的受力如图3所示，将各个力分解到沿AD面方向和垂直于AD方向。图4中R1为滑块ABC对滑块ABD的作用力，G2为滑块ABD重力，Q为挡土墙对填土的反作用力，f为

滑块ABD所受原自然坡面的摩擦力，可得到：

R=R1

(10)

Qcos(α-ε+θ)

(11)

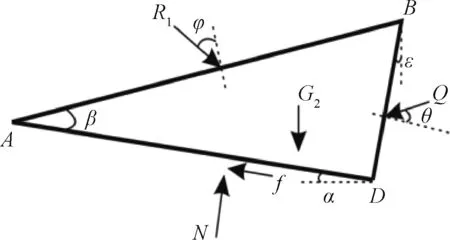
图3 滑块ABD受力Fig. 3 The stress of sliding block ABD

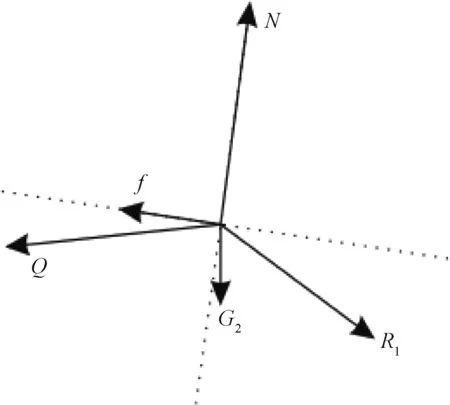
图4 滑块ABD受力分析Fig. 4 Force analysis of sliding block ABD

式中:θ——墙背外摩擦角;

μ——填土与原自然坡面间摩擦系数。

由式(5)(9)(10)(11)得：

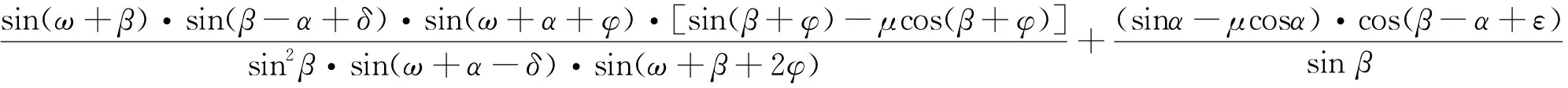
(12)

Q取极大值Qmax即为所求土压力。因此，可令：

(13)

通过Matlab软件可求得ω和β的值，代入式(12)，可得极限平衡状态的土压力计算公式：

水平方向上的分力为：

(14)

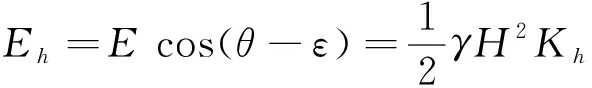
(15)

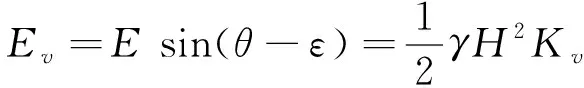
(16)

式中:Eh——土压力在水平方向上的分量;

Ev——土压力在竖直方向上的分量;

K——土压力系数;

Kh——水平土压力系数；

Kv——竖向土压力系数。

由上述分析推导过程与结果可见，本方法比塑性极限分析方法[9]概念简单，方便实际操作。

2 实例工程概况

衢宁铁路屏南车站高填方工程，属于较陡斜坡地基地段的大面积高填方工程，斜坡自然坡角约超过30°，最大填高约50 m(图5)。这在国内铁路工程建设中尚属首例。

图5 现场自然坡面Fig.5 The natural slope surface

图6为DK324+760断面示意图。填方边坡采用桩基托梁挡墙支挡，挡墙高7 m，墙宽2 m，墙背内倾，坡度为1∶0.25，托梁长20 m×宽3.45 m×高1.5 m，共布置4根截面为1.75 m×2 m的方桩，桩长为10 m，桩间距为2.6 m。下部桩基嵌固于基岩中，基岩为弱风化细粒花岗岩，灰色，块状构造；节理裂隙较发育，岩芯多呈柱状，偶夹块状。挡土墙墙后填土为AB组填料，填方高度为23 m，其物理力学指标如表1所示。

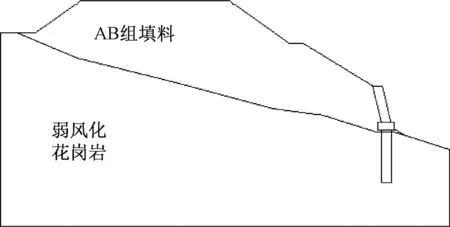
图6 DK324+760断面示意图Fig. 6 Diagram of cross section DK324+760

密度/(kg·m-3)黏聚力/kPa内摩擦角/(°)AB组填料2 000032弱风化花岗岩2 20030040

3 计算结果

针对该实际工程，各主要几何参数取值如表2所示。当填土处于极限平衡状态时μ=tanα，代入式(13)～(15)，可以得到斜坡填土体达到极限平衡状态时的破裂角ω=56°，β=32°，水平土压力系数Kh=7.33；若采用FRIEDLI等[9]的极限分析法计算，可得水平土压力系数为7.32，两者相对误差小于1.0%，说明本文算法具有合理性。

表2 工程实例主要几何参数取值

为进一步验证本文的计算方法，在ε=0°，φ=30°，α=5°，θ=25°，填方坡面倾角δ变化时，将本文算法与FRIEDLI方法、库伦土压力方法的计算结果进行比较(表3)。可见，取不同的δ时，本文的计算结果与FRIEDLI[9]的结果十分接近，而库仑土压力的结果与两者差异较大，说明库伦土压力公式不适用于此种填方的土压力，这与其适用条件的限制有关[15]。

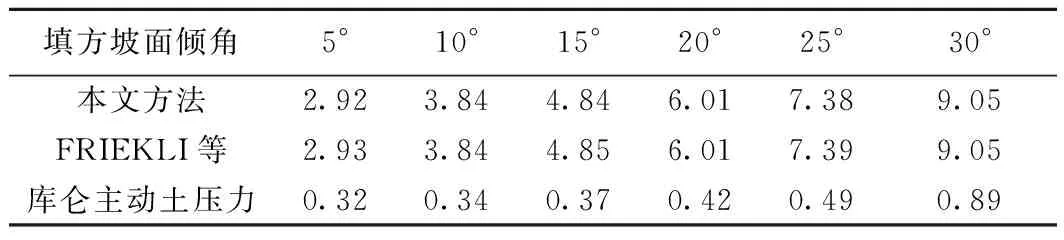
表3 水平方向土压力计算结果Table 3 The calculation results of horizontal earth pressure

4 影响因素分析

4.1 墙背外摩擦角

表4为挡土墙墙背外摩擦角取不同值时水平土压力系数的计算结果。其中，ε=0°、α=5°、δ=5°，μ=tanφ。

表4 墙背外摩擦角对水平土压力系数的影响Table 4 The influence of external friction angle of wall back on horizontal earth pressure coefficient

可见，墙背外摩擦角对水平土压力影响甚微，这与FRIEDLI[9]的结果一致。图7为相同条件下，竖向土压力系数的变化规律。可见，墙背外摩擦角越大，土压力的竖向分量越大，因此，挡土墙及下部结构稳定性验算时不可忽视墙背外摩擦角的影响。

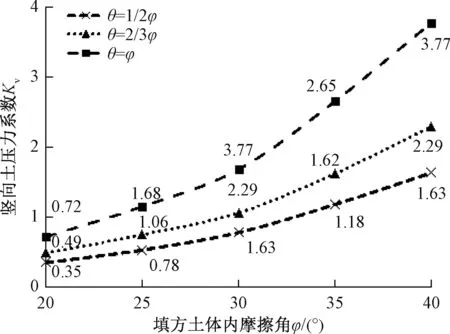
图7 填土内摩擦角及墙背外摩擦角对竖向土压力系数影响Fig.7 The influence of internal friction angle of backfill and external friction angle of the wall back on vertical earth pressure coefficient

4.2 坡面倾角与填土内摩擦角

图8为水平土压力系数的大小随坡面倾角δ的变化规律。其中，ε=0°、α=5°，μ=tanφ。

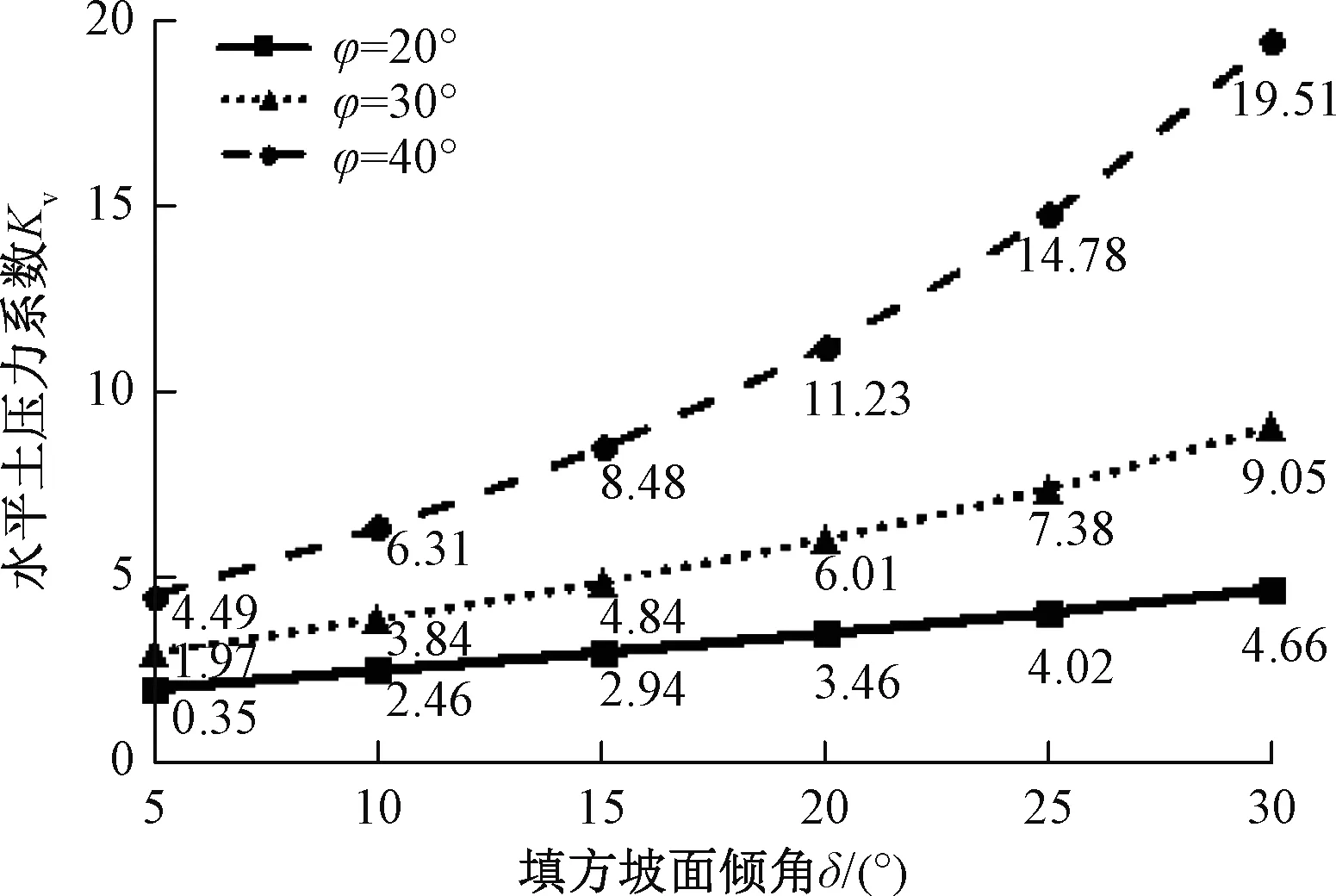
图8 水平土压力系数随填方坡面倾角变化曲线Fig. 8 The curve of horizontal earth pressure coefficient versus filled slope angles

可见，水平土压力系数Kh的大小随坡面倾角的增大而增大。填方坡面倾角越大，非线性增大特征越明显。填土内摩擦角φ越大，水平土压力系数越大，这与适用于墙后是均质无限填土的朗肯与库伦土压力理论完全不同，从而进一步说明经典的土压力理论不适于计算斜坡地基上填方土压力，其原因在于二者墙后土体的失稳破坏模式不同。

4.3 自然斜坡面倾角与墙背倾角

图9为水平土压力系数的大小随自然斜坡面倾角的变化规律。其中，φ=30°、δ=30°，μ=tanφ。可见，水平土压力系数随自然斜坡面倾角的增大而减小。相对而言，墙背倾角对水平土压力系数影响不大。

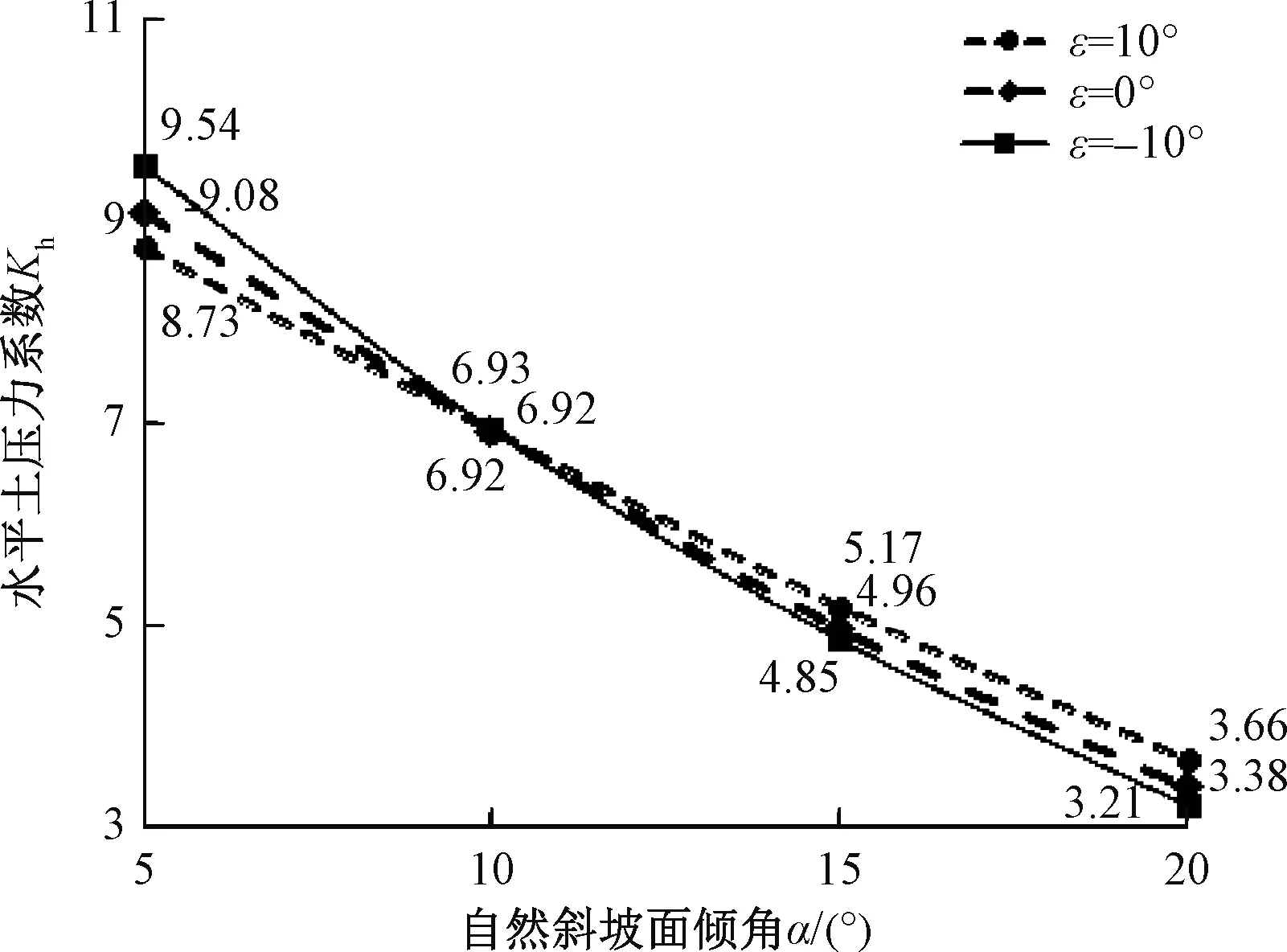
图9 水平土压力系数随自然坡面倾角变化曲线Fig. 9 The curve of horizontal earth pressure coefficient versus natural slope angles

4.4 挡土墙高度

由式(15)、(16)可知，挡土墙水平和竖向土压力系数与挡土墙高度无关，但水平和竖向土压力的大小均与挡土墙墙高的平方成正比。

图10给出了不同墙高情况下水平土压力的变化规律，其中φ=30°、δ=20°、γ=20 kN/m3。可见，随着墙高的逐渐增大，水平土压力大小呈非线性递增。

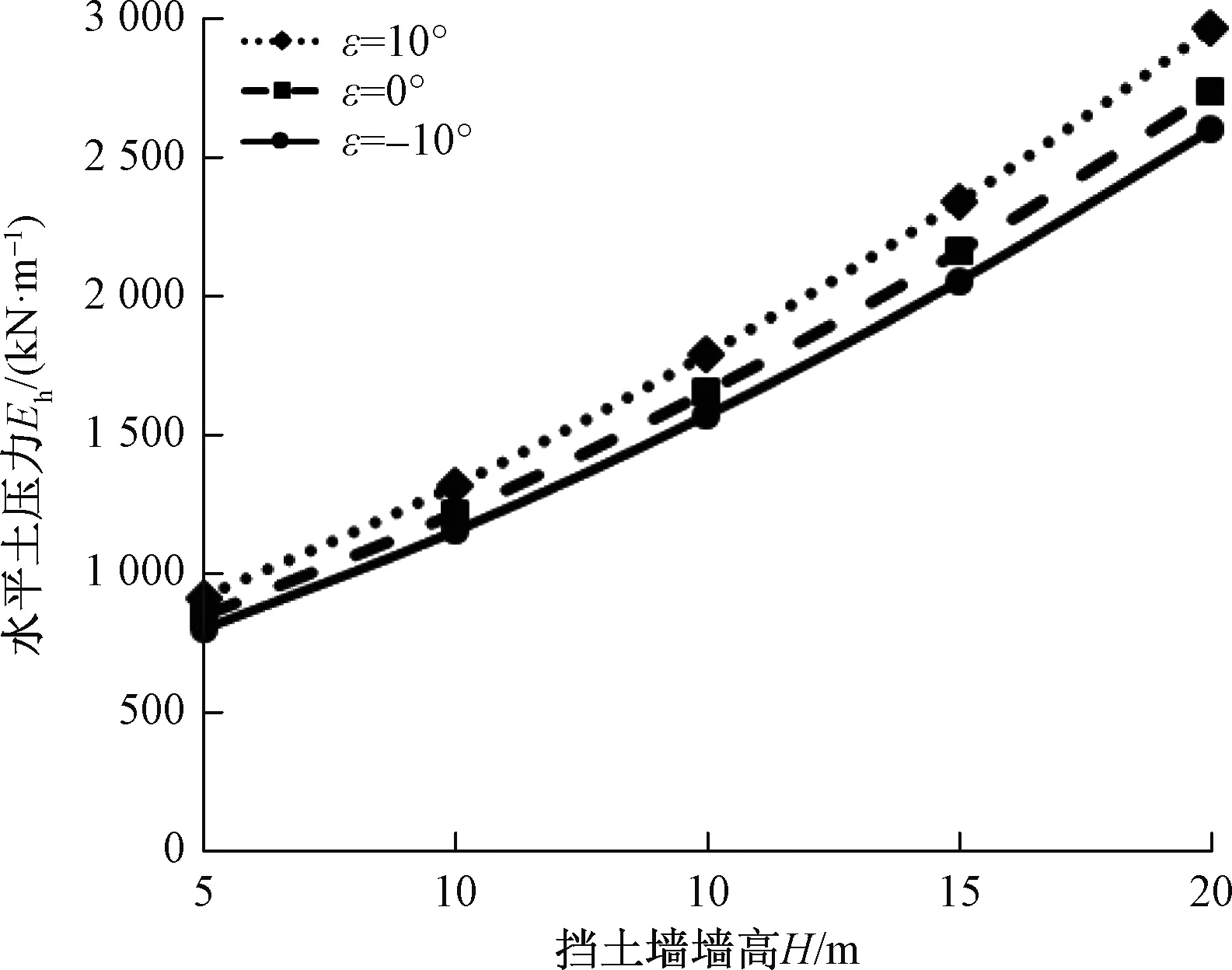
图10 水平土压力大小随挡土墙高度变化曲线Fig. 10 The curve of horizontal earth pressure versus height of the retaining wall

5 结论

针对斜坡地基上的填方边坡，基于其简化失稳破坏模式，可采用概念简单清晰的极限平衡方法分析作用于重力式挡土墙上侧向极限土压力，推导出计算公式，主要结论如下：

(1)对于挡土墙后斜坡高填方路基式，基于极限平衡方法，假定填土体发生“越顶”的失稳破坏模式，可得出挡土墙上极限水平土压力的计算方法。

(2)针对衢宁铁路屏南车站斜坡地基高填方工程，桩基托梁挡墙上土压力计算结果，与已有极限分析法所得结果的相对误差在1.0%以内，本文方法具有一定的合理性。

(3)挡土墙外摩擦角对极限土压力的水平分量影响甚微，而对竖向分量影响显著。填方坡面倾角、挡土墙墙背倾角、自然斜坡面倾角、填土内摩擦角是影响填土侧向极限土压力的重要因素。其中，填方坡面倾角、填土内摩擦角与水平土压力系数呈正相关；自然斜坡面倾角与水平土压力系数呈负相关；而墙背倾角对水平土压力系数影响相对不明显；极限土压力大小与墙高的平方呈正比。