一种改进超像素融合的图像分割方法

余洪山 张文豪 杨振耕 李松松 万琴 林安平

摘 要：基于超像素的传统图像分割方法在边缘分割的一致性、计算效率和融合算法的自适应性等方面仍存在诸多问题. 文章结合国内外相关研究进展，提出了一种新型超像素融合的图像分割方法. 方法采用ERS超像素过分割算法，以强度、梯度直方图作为超像素特征，并采取EMD方法计算特征距离，通过混合Weibull模型获取融合自适应阈值，进而完成分割. 算法时间复杂度降至为O（N），分割过程中不需要手动选取待分割区域，有效提高了算法的自适应性. 实验结果表明本方法在分割边界准确度和处理效率方面优于现有方法.

关键词：超像素；区域融合；陆地移动距离；混合Weibull模型；图像分割

中图分类号：TP273 文献标志码：A

Abstract：Traditional image segmentation methods based on superpixel still have many problems in terms of consistency of edge segmentation， computational efficiency and adaptability of merging algorithms. We combine domestic and foreign research advances and propose a novel superpixel merging image segmentation method， which adopts ERS superpixel oversegmentation algorithm and uses intensity and gradient histogram as superpixel features. Additionally， EMD method is used to calculate feature distance and the merging self-adaptive threshold is obtained by mixing Weibull model to complete the segmentation. As a result， the time complexity of proposed algorithm is reduced to O（N）， and the segmentation process is not required to manually select the region to be segmented. Compared with current methods， experiment results show that the proposed method has better performance on boundary accuracy and processing efficiency.

Key words：superpixel；region merging；earth movers distance；weibull mixture model；image segmentation

图像分割是利用颜色、纹理和灰度等特征将图像分割成一定数量的符合人类视觉感知分类的区域. 由于自然图像中场景的复杂性，加之人的视觉感知上的主观性，人们对图像场景理解不尽相同，因此图像分割一直是计算机视觉中的一个难点. 传统方法以像素为基本处理单元，使得算法时间消耗大、效率低. 超像素是指具有相似纹理、颜色和亮度等特征的相邻像素构成的图像块[1]，它利用像素之间特征的相似程度将像素分组，在很大程度上降低了后续图像处理任务的复杂度. 然而超像素分割会对图像产生过分割，并不能达到符合人的视觉感知的分割结果. 超像素算法多用于图像分割预处理，在后续图像处理中用超像素来代替像素，大大降低了时间的消耗.

目前，基于超像素融合的圖像分割研究开始获得越来越多的关注，典型方案有基于SLIC或Normalized cuts产生超像素过分割，然后提取超像素的特征（颜色、纹理和直方图等），再基于一定的相似性度量标准计算相邻两个超像素的特征相似性距离. Hsu C Y等[2]提出了基于谱聚类的融合策略，该方法通过对SLIC 产生的超像素进行谱聚类取得了较高的效率，但其对于复杂场景的分割结果不够理想. Song X等[3]采用了基于分层超像素的区域融合策略-MSRM（maximal similarity based region merging）[4]，针对前景对象很少的图像，该方法可以得到较好的分割结果，但需要人为给定前景对象所在的大致矩形区域. 当场景前景对象很多且分散时，该算法将很难处理，因此存在很大的局限性. Han B等[5]利用Normalized cuts[6]产生超像素，基于直方图的相似性度量计算相邻超像素间的非相似性距离来完成对图像的分割. 该方法虽然对相似的超像素进行了融合，但是融合比较保守导致分割结果过于细化，即在明显应该分割为一个对象的区域中存在没有融合的超像素边界. 综上所述，目前基于超像素融合的图像分割方案在边缘分割的一致性、特征相似性度量的可靠性、计算效率和融合算法的自适应性方面仍需进一步改善.

针对上述问题，本文结合国内外相关研究进展，提出了一种改进超像素融合的图像分割方法. 主要改进如下：1）本文采用ERS（entropy rate superpixel）算法生成与真实边缘一致性更佳的超像素图像；2）选用稳定性好且计算简易的直方图特征（强度、颜色及方向直方图），并采用陆地移动距离EMD（Earth Movers distance）计算超像素节点间相似性，以适应多种结构尺寸；3）采用Weibull 模型对相邻超像素的EMD 分布进行估计，获取融合处理的自适应阈值，从而提高了本文算法的鲁棒性. 本文算法时间复杂度为O（N），处理过程中不需要手动选取待分割区域，分割结果的边界准确率和处理效率均具有明显的提高.

1 改进的超像素融合图像分割方法

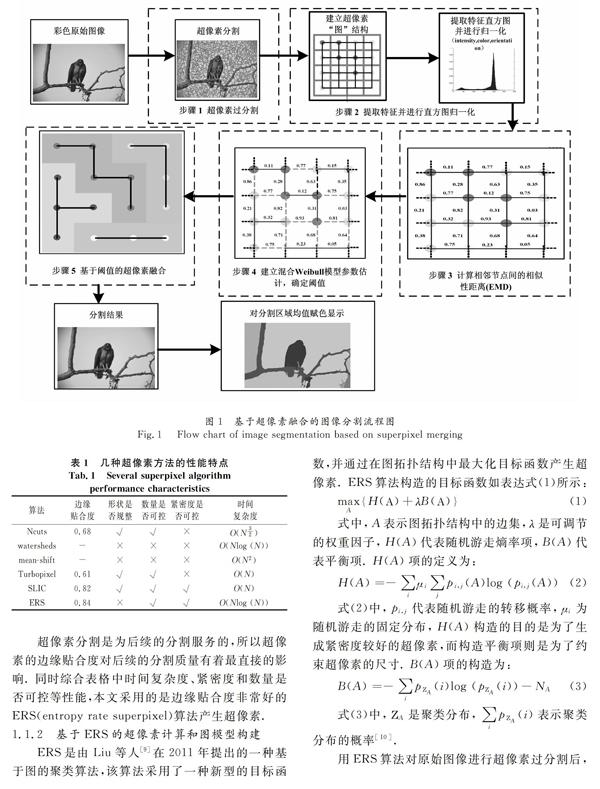
如图1 所示，本文提出的超像素融合图像分割方法可划分为三部分：1）超像素过分割方法选择及图像预分割；2）以超像素节点为单位，求取强度、颜色以及方向（梯度）的特征直方图，基于特征相似性距离EMD模型，计算相邻节点各自特征直方图之间的相似性距离；3）建立Weibull 混合模型（Weibull mixture model），对模型中的参数进行估计，确定节点特征相似性距离阈值γf ，并根据其进行超像素融合.

1.1 基于超像素算法的图像预分割

1.1.1 超像素算法选择

目前，超像素算法主要分为两大类：基于图论的算法和基于梯度上升的算法.超像素的评价标准[7]主要包括：1）边缘贴合度；2）紧密度；3）计算效率等. 边缘贴合度指的是超像素边缘与真值边沿的吻合程度. 某些超像素方法虽然可以产生超像素，但是超像素的边缘可能穿过场景中物体的实际边缘. 紧密度反映了超像素形状是否规则以及边缘平滑程度. 常见的超像素算法性能比较[7]如表1 所示（使用公测数据集Berkeley dataset[8]中图片进行测试，其中边缘贴合度通过边界召回率boundary recall[7]反映）.

1.2 特征提取与相似性度量

1.2.1 超像素节点特征提取

在二维彩色图像中，颜色、强度以及方向梯度是三种常用且易提取的直方图特征. 超像素是一定范围内像素点的集合，因此本文选取强度直方图、颜色直方图和方向直方图特征作为超像素节点特征.强度直方图是一个1维256区间的直方图，颜色直方图是由色调（hue）和饱和度（saturation）（HSV颜色空间中）构成的76*76（颜色位数为8位）的2维直方图，梯度直方图是用方向梯度（即垂直方向梯度与水平方向梯度的反正切）构成的1 维的360 区间的直方图，这个特征与HOG 特征类似. 为便于计算处理，算法将所有的特征直方图归一化处理.

1.2.2 基于EMD的相似性度量

1）EMD度量标准

为了计算上述特征直方图相似性从而为超像素融合提供判断依据，本文采用EMD作为相似性度量标准. EMD是一种在某种区域两个概率分布距离的度量，即被熟知的Wasserstein度量标准. 如果两个分布被看作在区域上两种不同方式堆积一定数量的山堆，那么EMD是把一堆变成另一堆所需要移动单位小块最小的距离之和.

2.2 Weibull模型的有效性分析

为了验证本文算法加入Weibull模型的有效性，本文另通过手动选取相似性阈值γf ，对不同场景图像进行超像素融合实验. 实验结果（超像素融合后的均值填充效果图）如图6所示.

图6中最右侧为与真实场景最一致的融合效果图. 由实验结果可知，要得到良好的融合效果，必须手动调节多次阈值直至结果满意为止. 而且，对于不同场景的图像，其最佳相似性阈值不尽相同.

加入Weibull模型后，最佳相似性阈值可由Weibull分布估计求得. 与上述手动调节阈值相比，具有更好的灵活性，避免了繁琐的调节阈值的步骤，可方便应用于不同的场景图像，极大地提高了算法的鲁棒性.

2.3 分割结果直观效果对比

为了验证本文算法的分割效果，本文选取了2种常用的基于超像素融合的分割算法并与其进行了对比，分别为DBSCN算法[18]对SLIC超像素融合的分割方法（SLICDBSCN），基于原型对象（protoobject）的分割方法[12]（PO）.

不同算法的实验结果对比如图7所示，其中（a）为原始图像，（b）、（c）和 （d）分别为SLICDBSCN算法、PO算法以及本文算法的分割结果. 超像素数目均设定为600. 由图7中分割结果的对比可得，在产生相同超像素个数的情况下，本文方法得到的分割結果在保持边界的性能上优于SLICDBSCN算法和PO方法，分割结果视觉效果上更符合人的视觉感知. 图8为图7的局部细节放大对比. 进一步从分割细节上进行了对比说明.

2.4 分割结果性能量化对比

为了对实验结果进行量化评价，本文采用了3种量化指标：1）PRI（Probabilistic Rand Index）[19]，它统计了实验的分割结果的边界标记像素与真实分割结果保持一致的数目，即分割结果的边缘准确度；2）VOI（Variation of Information）[20]，该指标针对两个类之间的信息的不同进行了距离度量；3）BDE（Boundary Displacement Error）[21]，该指标表示分割结果与真值之间的区域边界的平均位移.

从以上指标可以得出，PRI越高，VOI，BDE越小，则分割结果的性能越好. 本文分割方法与Normalized cut（Ncut）[6]，Mean Shift[22]，Ultrametric Contour Maps（UCM）[23]，Segmentation by Aggregating Superpixels （SAS）[24]，SLICDBSCN算法以及PO算法的量化比较如表2所示，其中文献[6]、[22]、[23]、[24]的性能量化数据来自于文献[2]，实验数据集采用BSD.

由表看出，本文算法具有较高的时间效率，相较于SLICDBSCN算法具有明显的优势，与PO算法相差无几. 随着超像素的数目增多，时间消耗亦随之增加，虽然N越大，超像素对边缘的贴合度越好，但是并不是对任何图像都将超像素的数目N设置的越大越好，对于图像尺寸较小时，如BSD数据集的尺寸为481×321，N设置600即可获得很好的分割结果.

3 结 论

本文在图像预处理阶段（超像素分割）采用了ERS算法，通过产生数目更少的超像素便可达到更好的边缘保持性能，这一点对后续的分割至关重要.

此外，本文的算法充分運用了统计学，距离度量采用EMD ，通过 Weibull分布建立EMD统计模型.因此，该方法的实验结果具有很高的边缘准确性. 本文采用AIC信息准则确定自适应阈值，无需手动调节，从而提高了超像素聚类的鲁棒性，使得该算法能够适应复杂场景的分割. 在时间消耗上，本文的分割方法首先采用ERS超像素过分割，使得后续的融合都是基于超像素级的. 另外，本文的分割方法两次利用了“图”的结构（ERS为第一次利用“图”结构，然后基于超像素过分割的结果第二次建立“图”的结构），这使得我们的算法具有很好的存储效率.

与其他经典的传统分割算法（[22]，[23]，[24]）以及基于超像素融合的分割方法（[2]，[12]，[18]等）的实验结果进行对比，本文对图像的分割结果性能优于其他方法，特别是在图像场景比较复杂的情况下，本文的分割结果对物体的边界保持得非常好. 在对超像素融合后，将各个区域进行均值赋色，最后生成的分割图像的视觉效果和人类视觉的感知一致.

参考文献

[1] MALIK J. Learning a classification model for segmentation[J]. Proc Iccv， 2003，1（1）：10-17.

[2] HSU C Y， DING J J. Efficient image segmentation algorithm using SLIC superpixels and boundaryfocused region merging[C]// Communications and Signal Processing. Melmaruvathur： IEEE， 2014：1-5.

[3] SONG X， ZHOU L， LI Z， et al. Interactive image segmentation based on hierarchical superpixels initialization and region merging[C]// International Congress on Image and Signal Processing. Dalian： IEEE， 2015： 410-414.

[4] NING J， ZHANG L， ZHANG D， et al. Interactive image segmentation by maximal similarity based region merging[J]. Pattern Recognition， 2010， 43（2）： 445-456.

[5] HAN B， YAN J. A novel segmentation approach for color images with progressive superpixel merging[C]// International Conference on Computer Science and Network Technology. Changchun： IEEE， 2013： 433-437.

[6] SHI J， MALIK J. Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2000， 22（8）： 888-905.

[7] ACHANTA R， SHAJI A， SMITH K， et al. SLIC superpixels compared to stateoftheart superpixel methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2012， 34（11）： 2274-2282.

[8] MARTIN D， FOWLKES C， TAL D， et al. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics[C]// International Conference on Computer Vision.Vancouver： IEEE， 2001， 2： 416-423.

[9] LIU M Y， TUZEL O， RAMALINGAM S， et al. Entropy rate superpixel segmentation[C]// Computer Vision and Pattern Recognition.Colorado ： IEEE， 2011： 2097-2104.

[10]RUBNER Y， TOMASI C， GUIBAS L J. A metric for distributions with applications to image databases[C]// International Conference on Computer Vision. Bombay： IEEE Computer Society， 1998：59.

[11]LEVINA E， BICKEL P. The earth mover's distance is the mallows distance： Some insights from statistics[C]//

Eighth IEEE International Conference on Computer Vision. Vancouver： IEEE， 2001， 2： 251-256.

[12]BURGHOUTS G J， SMEULDERS A W M， GEUSEBROEK J M. The distribution family of similarity distances[C]//

Conference on Neural Information Processing Systems.Vancouver： DBLP， 2009：201-208.

[13]YU C P， HUA W Y， SAMARAS D， et al. Modeling clutter perception using parametric protoobject partitioning[C]// International Conference on Neural Information Processing Systems. Lake Tahoe： Curran Associates Inc， 2013：118-126.

[14]NELDER J A， MEAD R. A simplex method for function minimization[J]. The Computer Journal， 1965， 7（4）： 308-313.

[15]LAGARIAS J C， REEDS J A， WRIGHT M H， et al. Convergence properties of the NelderMead simplex method in low dimensions[J]. SIAM Journal on Optimization， 1998， 9（1）： 112-147.

[16]LUMLEY T， SCOTT A. AIC and BIC for modeling with complex survey data[J]. Journal of Survey Statistics and Methodology， 2015， 3（1）： 1-18.

[17]XIAO J， HAYS J， EHINGER K A， et al. Sun database： Largescale scene recognition from abbey to zoo[C]// Computer Vision and Pattern Recognition. San Francisco： IEEE， 2010：3485-3492.

[18]ESTER M. A densitybased algorithm for discovering clusters in large spatial Databases with Noise [C]// International Conference on Knowledge Discovery and Data Mining. Portland： AAAI Press， 1996：226-231.

[19]UNNIKRISHNAN R， PANTOFARU C， HEBERT M. Toward objective evaluation of image segmentation algorithms[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2007， 29（6）：929.

[20]MEIL M. Comparing clusterings： an axiomatic view[C]//Proceedings of the 22nd International Conference on Machine Learning. Bonn： DBLP， 2005： 577-584.

[21]FREIXENET J， MUOZ X， RABA D， et al. Yet another survey on image segmentation： region and boundary information integration[J]. Lecture Notes in Computer Science， 2002， 2352：21-25.

[22]COMANICIU D， MEER P. Mean shift： A robust approach toward feature space analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2002， 24（5）： 603-619.

[23]ARBELAEZ P， MAIRE M， FOWLKES C， et al. From contours to regions： An empirical evaluation[C]//Computer Vision and Pattern Recognition. Miami： IEEE， 2009： 2294-2301.

[24]LI Z， WU X M， CHANG S F. Segmentation using superpixels： A bipartite graph partitioning approach[C]// Computer Vision and Pattern Recognition. Rhode Island： IEEE， 2012：789-796.