PEMFC密封胶接触压力的均匀性研究及改善方法
2018-12-26张智明胡淞李昆朋张云瀚杨代军
张智明 胡淞 李昆朋 张云瀚 杨代军

摘 要:针对质子交换膜燃料电池密封胶接触压力分布均匀性的问题,采用Fujifilm公司的压力膜测试了4个单电池片数不同的电堆的密封胶接触压力分布,利用MATLAB中搭建的平台对测试结果可视化;并基于MooneyRivilin超弹性材料本构模型建立了密封胶平面和电堆截面的有限元模型;利用有限元模型,设计了带圆弧和圆环的密封胶平面结构参数;并给出了沿集成力方向利于接触压力均匀分布的不同层密封胶初始厚度修正值的计算方法.结果表明:单电池平面内密封胶接触压力的最大差值为1.2 MPa;沿集成力方向,靠近端板处的密封胶接触压力较中间层数的大,且层数越多的电堆,处于同一层数的双极板与密封胶的接触压力越小;在接触面积一样时,加圆弧结构的密封胶在平面内的接触压力标准差比原来结构的标准差小41%,加圆环的比原来结构小30%;对于不同层数电堆,密封胶初始厚度修正后的接触压力值均在最佳值附近.
关键词:燃料电池;密封胶;均匀性;超弹性模型;结构设计
中图分类号:TK91 文献标志码:A
Abstract:Aiming at improving the uniformity of sealant′s contact pressure distribution for the proton exchange membrane fuel cells, the contact pressure distribution in the four stacks with different layers was tested using a Fujifilm pressure membrane. The test results were visualized by using the platform built in Matlab. Based on the MooneyRivilin superelastic material constitutive model, finite element models of the sealant plane and the stack cross section were established, which were used to design the sealant structure with arcs and rings. Equations for correcting the initial sealant thickness were given in which the uniformity of contact pressure along the integrated force was improved. The results show that the maximum difference in the contact pressure of the sealant in the plane is 1.2 MPa. Along the integrated force, the contact pressure near the end plate is greater than that in the intermediate layers and the more layer results in the lower contact pressure at the same layer. When the contact area is the same, the standard deviation of sealant pressure in plane with the arc structure is 41% less than that of the original structure, and the ring is 30% less than the original structure. For different layers of the stack, the contact pressure after correcting the initial thickness of the sealant maintains around the best. This study can provide a kind of sealing structure that maintains the consistent performance in the fuel cell stack.
Key words:fuel cell;sealants;uniformity;superelastic model;structural design
目前,質子交换膜燃料电池(PEMFC)技术已经取得重大进步,但是质子交换膜电池的性能、成本、耐久性仍是制约其商业化的关键因素.在燃料电池性能方面,集成力对燃料电池各部件的影响仍是制约整堆性能提高的重要方面.作为集成力在电堆内部最主要的承力和传力部件,密封胶的接触压力分布主要影响燃料电池的气密性,并进一步影响燃料电池的电化学性能[1-2].
目前,国内外专门针对质子交换膜燃料电池密封胶的接触压力研究还很少,但在普通密封胶圈的有限元仿真及电堆内部接触压力分布两方面有一定的进展.张智明等[3]通过有限元方法分析了影响密封胶密封性能的影响因素.陈占清等人[4]利用有限元分析软件 ANSYS 对 O 形橡胶密封圈在不同压缩率下的接触压力分布进行分析;韩传军等[5]则利用Abaqus分析初始压缩率对矩形橡胶密封圈变形、接触应力和等效应力的影响,并对密封圈形状做了圆角优化.夏卫明等[6]从高阶低阶单元的应用、网格密度、接触刚度及接触算法、载荷步与载荷子步几个方面对密封胶非线性计算收敛性问题进行了讨论.
Banerjee等人[7]用实验的方式研究螺栓力矩及扩散层材质对燃料电池性能的影响时,提到了密封胶垫对接触压力的分布有影响,但没通过专门的试验来验证.Ismail等人[8]研究了在集成力下,密封胶压缩率对气体扩散层(GDL)力学行为的影响.Bates等人[9]对一个含16个单电池的电堆仿真时,得到靠近端板的单电池及最中间的单电池各部件的最大压力,结果表明密封胶垫是除端板外承受压力最大的部件.Millichamp等人[10]指出密封胶厚度和压缩率对GDL区域压力的分布有重要影响.杨全勇等人[11]研究了一个单电池在不同密封胶厚度下,双极板和GDL的接触情况以及极化曲线.
为研究质子交换膜燃料电池密封胶接触压力的均匀性,本文通过实验和有限元仿真的方法分别得到包含50片、70片、90片、110片单电池的4个电堆在集成力下内部的压力分布状态,发现了密封胶在单电池平面以及沿集成力方向存在压力分布不一致的现象,并对密封胶的平面结构和厚度进行改善设计;改善密封胶压力分布的均匀性,从而提高膜电极和双极板之间接触压力均匀性.
1 密封胶接触压力试验
1.1 试验准备
通过压力膜试验可对燃料电池电堆在集成力下各部件压力分布展开研究.为了研究密封胶在集成力下的接触压力分布规律,本节对不同层数(50层、70层、90层、110层)电堆进行了压力膜试验.
由于每个电堆包含的单电池比较多,且有研究表明[12]:靠近端板的单电池接触压力大,中间位置的单电池接触压力小,故本试验的压力膜在4个电堆中的放置位置分布如下:50层电堆在电堆第1、2、4、9、16、25层布置压力膜,70层电堆在此基础上增加第35层布置压力膜,以此类推,每隔10层布置压力膜.
1.2 压力膜接触压力量化处理方法
根据Fujifilm公司提供的压力膜温湿度特性以及颜色密度与压强值对应曲线,可知LLW压力膜的测量范围为0.5~2.5 MPa,温度允许区间为0~40 ℃.在得到密封胶的试验图片后,需将图片中红色密度的高低转换成压强值,从而可以得出量化的试验结果,本文中颜色密度与压力转换的过程如图1所示.
在MATLAB中可编程实现颜色密度与压力的转换,并编写程序设计出可视化平台,如图2所示.根据该可视平台可快速得到密封胶平面的压力分布值.
1.3 试验结果及分析
图3中显示的是4个电堆第2层密封胶平面受压后的压力膜结果,其他层结果类似.图3(a)(c)(e)(g)是由试验直接得到的密封胶受压后压力膜的图像,图3(b)(d)(f)(h)是经可视化平台转换过的密封胶压力分布图.
由图3(b)(d)(f)(h)可知,在装配力作用下,密封胶平面内接触压力平均值和最大值相差较大,最大差值为1.2 MPa;说明密封胶接触压力存在不一致分布,在螺栓紧固的位置以及密封胶拐角处均存在应力集中现象.
图3只是针对不同电堆第2层密封胶接触压力在单电池平面上的分布.根据压力膜量化处理方法,可统计不同电堆不同层数的密封胶的平均接触压力,从而得到不同节电池电堆内密封胶的接触压力分布规律,如图4所示.
由图4可以看出密封胶的接触压力在集成力方向上存在不一致现象.对于同一电堆来说,随着节电池层数的增加,双极板与密封胶间接触压力略有下降,靠近端板处的密封胶接触压力比较大.这是由于螺栓装配力造成端板变形,从而增大电堆靠近端板处的密封胶接触压力.
从图4还可看出,对于包含不同层数的电堆,层数越多的电堆,处于同一层数的双极板与密封胶的接触压力越小;这是由于单电池片数越多,整堆的等效刚度越大,密封胶与双极板总的接触面积也增加,在同样的外部载荷下密封胶的变形和应力都会变小.
2 密封胶接触压力有限元仿真
实验中电堆层数较多,若采用三维有限元模型,则网格数量巨大,计算耗时长,不利于后续的优化设计.因此对电堆结构进行合理简化,建立二维电堆模型,将得到的仿真结果和试验结果比较,从而验证简化有限元模型的有效性,便于后续的优化.
2.1 密封胶模型及材料特性
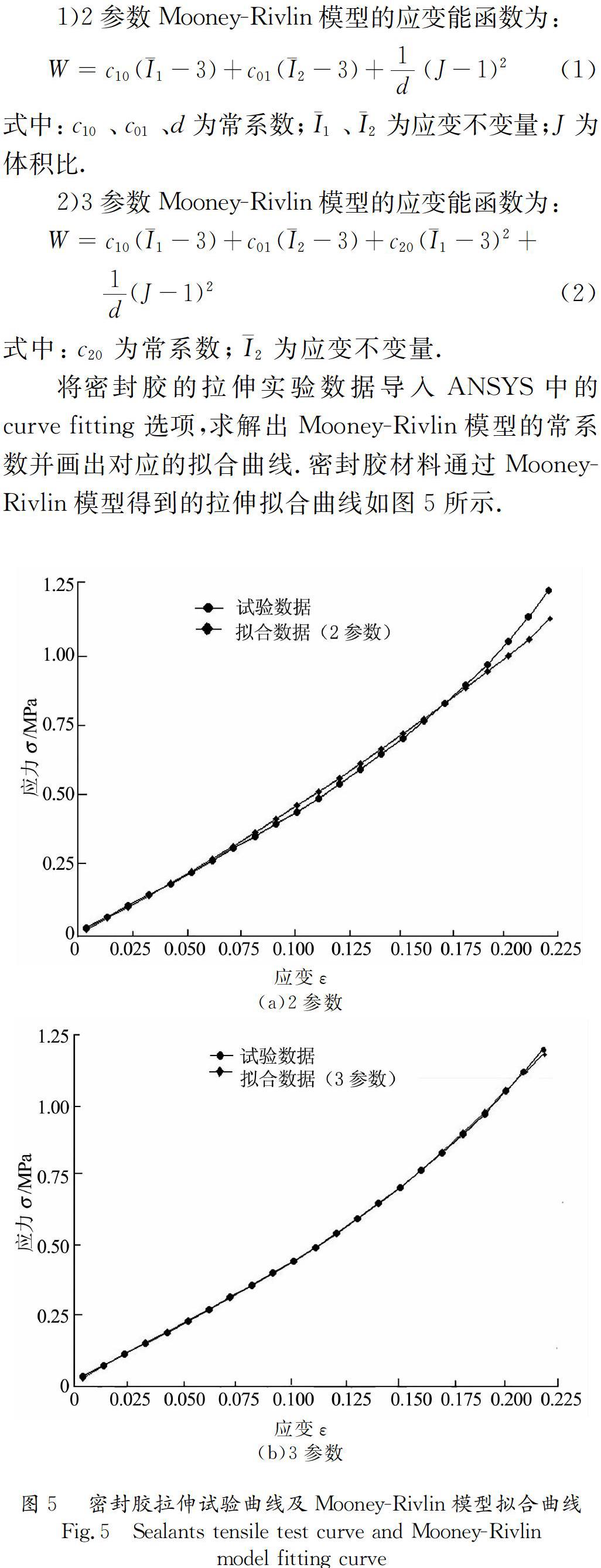
由于采用的密封胶是硅橡胶,材料属性是超弹性的,密封胶的拉伸曲线如图5所示.MooneyRivlin模型几乎可以模拟所有橡胶材料的力学行为,适合于中小变形,一般适用于应变约100% (拉伸)和30%(压缩)的情况;常用的MooneyRivlin模型有2、3、5及9参数模型,且较多参数的模型对于较大应变的求解,可得到较好的近似[13].文中密封胶的压缩率为20%,所以考虑用2或3参数的MooneyRivlin模型,对应的应变能函数如下.
2.2 单电池全尺寸密封胶接触压力分布
建立密封胶在单电池平面内的全尺寸密封胶有限元模型来分析燃料电池双极板和密封胶之间的接触压力分布情况.由于研究针对密封胶受力分析,可忽略双极板脊背对密封胶接触压力分布的影响,故双極板模型简化为平板,密封胶尺寸为137 mm×245 mm×0.65mm,建立双极板密封胶几何模型和网格化后的有限元模型如图6所示.
与压力膜试验结果(图7(a))对比,数值仿真结果(图7(b))中应力集中的地方是一致的,且应力的均值均在1.6 MPa左右,说明了该平面全尺寸密封胶模型可以用来分析密封胶接触压力在平面的分布情况.试验结果测得的最大压力比仿真结果小是因为试验采用的压力膜量程为0.5~2.5 MPa,但从图7(b)看出测试区域有很小部分超出量程.从图7(b)中可看出在螺栓紧固式电堆的密封胶平面上,离布置螺栓位置较近的区域应力相对其他地方更大,产生应力集中,其中拐角处应力集中尤为显著.
2.3 电堆密封胶接触压力分布
建立二维电堆模型来分析密封胶接触压力在集成力方向上的分布情况.为简化模型离散化过程,端板为矩形,双极板为梯形直流道,密封胶采用半圆形截面.建立电堆的1/4有限元模型如图8所示,含有15片单电池;由于本文的模型是通过APDL参数化建立的,对于50层、70层、90层、110层电堆通过修改参数即可实现.
最终统计出电堆每一层双极板和密封胶的平均接触压力,得到如图9所示的结果.对比图9和图4可发现,由电堆二维模型得到的沿螺杆集成力方向的密封胶接触压力分布情况同试验是一致的;所不同的是在图4中,处于第1层和最中间层之间的单电池接触压力有些波动,而图9中的仿真结果则比较平稳;这是由于仿真能保证每层都是用同一属性的材质和同一厚度的密封胶,而实际电堆则可能出现微小差异,从而造成压力分布的波动.所以用图8所示的双极板密封胶模型来研究密封胶接触压力在集成力方向上的接触压力是可行的.
3 密封胶接触压力均匀性改善方法
3.1 密封胶平面结构改善
为提高密封胶接触压力在平面内的均匀性,降低试验和数值仿真中出现的应力集中,增大密封胶受力接触面积,在燃料电池密封胶结构设计上,对密封胶应力集中处分别加圆弧和圆环进行处理.通过设计圆弧和圆环的半径,使得2种方案的接触面积大小一致.密封胶平面结构改善部分的尺寸如图10所示,未标注尺寸的部分与改善前的保持一致.
为了更直观地对比结构改善前后压力分布的优劣,将密封胶根据结构划分为12个区域来评估密封胶的接触压力均匀性.根据数值仿真模型分别求出各个区域压力的标准差,如图11所示.
由图11可知,加圆弧和圆环的密封胶结构都可以改善应力集中,使密封胶受力更加均匀.在两种结
构接触面积一样时,加圆弧的密封胶结构接触压力标准差比原来结构的标准差小41%,加圆环的密封胶结构接触压力标准差比原来结构的标准差小30%,所以加圆弧的效果优于加圆环.
3.2 密封胶初始厚度修正
由于密封胶结构可以改变其在电堆内的接触压力分布,为使电堆接触压力在集成力方向上趋于一致,可以通过改变每层密封胶初始厚度进行匹配.
按上述方法修正密封胶厚度后,对有限元模型重新进行仿真,并统计不同层数电堆在各个接触面上的平均接触压力,得到结果如图13所示.从图13可发现经过分模块修正后的密封胶厚度设计更有利于接触压力的均匀性分布,且所有层密封胶的接触压力值都在1.165 MPa附近.针对密封胶厚度修正的方法可提高电堆内接触压力分布均匀性.
4 结 论
1)PEMFC密封胶受到的接触压力在单电池平面存在分布不一致现象,最大差值达1.2 MPa,并且应力集中主要发生在紧固螺栓区域附近.
2)在密封胶平面加圆弧或圆环增大密封胶受力面积的方法,能降低密封胶平面内接触压力的应力集中现象,且圆弧效果优于圆环.
3)沿电堆集成力方向分层设计密封胶初始高度,有利于提高整个电堆密封胶接触压力分布的均匀性.
參考文献
[1] YE D H,ZHAN Z G.A review on the sealing structures of membrane electrode assembly of proton exchange membrane fuel cells[J].Journal of Power Sources,2013,231(13):285-292.
[2] 叶东浩,詹志刚,汪广进,等.低温燃料电池用质子交换膜的气体渗透性研究[J].湖南大学学报(自然科学版),2013,40(3):71-75.
YE D H,ZHAN Z G,WANG G J,et al.Effect on the gas permeation of proten exchange membranee in lowtemperature PEMFCs[J].Journal of Hunan University(Natural Sciences),2013,40(3):71-75.(In Chinese)
[3] 张智明,张娟楠.PEMFC金属双极板密封设计的有限元仿真[J].中国科技论文,2017,12(16):1895-1901.
ZHANG Z M,ZHANG J N.Finite element method modeling on sealant design of PEMFC metal bipolar plate[J].China Sciencepaper,2017,12(16):1895-1901.(In Chinese)
[4] 陈占清,詹永麒,朱昌明.压缩率对O形橡胶密封圈密封性能的影响[J].流体传动与控制,2007(2):46-48.
CHEN Z Q,ZHAN Y Q,ZHU C M.Effects of compressive rate on sealing characteristic of Oring[J].Fluid Power Transmission and Control,2007(2):46-48.(In Chinese)
[5] 韩传军,张杰.矩形橡胶密封圈的有限元分析及优化[J].橡胶工业,2013,60(2): 98-103.
HAN C J,ZHANG J.Finite element analysis and optimization of rectangle rubber seal[J].Rubber Industry,2013,60(2):98-103.(In Chinese)
[6] 夏卫明,骆桂林,嵇宽斌.橡胶结构有限元分析收敛问题的对策[J].机械设计与制造,2013,85(7):265-268.
XIA W M,LUO G L,JI K B.Countermeasures of the convergence problems in rubber structures FEA[J].Machinery Design & Manufacture,2013,85(7):265-268.(In Chinese)
[7] BANERJEE R,HINEBAUGH J,LIU H,et al.Heterogeneous porosity distributions of polymer electrolyte membrane fuel cell gas diffusion layer materials with ribchannel compression[J].International Journal of Hydrogen Energy,2016,41(33):14885-14896.
[8] ISMAIL M S,HASSANPOUR A,INGHAM D B,et al.On the compressibility of gas diffusion layers in proton exchange membrane fuel cells[J].Fuel Cells,2012,12(3):391-397.
[9] BATES A,MUKHERJEE S,HWANG S,et al.Simulation and experimental analysis of the clamping pressure distribution in a PEM fuel cell stack[J].International Journal of Hydrogen Energy,2013,38(15):6481-6493.
[10]MILLICHAMP J,MASON T J,NEVILLE T P,et al.Mechanisms and effects of mechanical compression and dimensional change in polymer electrolyte fuel cells:A review[J].Journal of Power Sources,2015,284(15): 305-320.
[11]楊全勇,余意,詹志刚.密封层厚度对国产材料燃料电池性能影响[J].电池工业,2011(3): 172-175.
YANG Q Y,YU Y,ZHAN Z G.Effects of gasket thickness on the performance of PEMFC with domestic materials[J].Chinese Battery Industry,2011(3):172-175.(In Chinese)
[12]ALIZADEH E,BARZEGARI M M,MOMENIFAR M,et al.Investigation of contact pressure distribution over the active area of PEM fuel cell stack[J].International Journal of Hydrogen Energy,2016,41(4): 3062-3071.
[13]张庆余,张洪伟,高相胜.ANSYS非线性有限元分析方法及范例应用[M].北京:中国水利水电出版社,2013:105-111.
ZHANG Q Y,ZHANG H W,GAO X S.Nonlinear finite element analysis method and application by ANSYS[M].Beijing:China Water Conservancy and Hydropower Press,2013:105-111.(In Chinese)
