离子色谱法测定地下水中硝酸盐氮含量的不确定度评定

俞建国

(中国地质科学院岩溶地质研究所 国土资源部广西岩溶动力学重点实验室，广西 桂林 541004)

水中“三氮污染”的分析和治理是目前研究的热点之一. 地下水环境中，主要的氮化合物有硝酸盐氮(NO3--N)、氨氮(NH4+-N)和亚硝酸盐氮(NO2--N)，即通常所说的“三氮”，并且以NO3--N为主要存在形式，浓度高时可达每升数十毫克. 随着社会工农业的不断发展，农村和城市的地下水都遭受到了以NO3--N为首的三氮污染，使得地下水的环境日趋严重[1]. 为了充分了解地下水“三氮污染”的现状，水中三氮的分析测试技术尤显重要，而氮污染的浓度又是研究氮循环的关键，因此准确测定三氮特别是硝酸盐氮的浓度非常重要.

国内水中硝酸盐的标准测定方法主要有酚二磺酸法、镉柱还原法、离子色谱法、气相分子吸收光谱法麝香草酚(百里酚)分光光度法和紫外分光光度法等[2]. 离子色谱法是20世纪70年代中期发展起来的一种新的液相色谱技术，具有分析速度快、灵敏度高、选择性好、样品用量少和易实现自动化等优点[3].

分析结果的不确定度[4-5]是分析测试质量控制环节中不可缺少的定量评定参数之一. 本文依据HJ 84-2016《水质 无机阴离子(F-、Cl-、NO2-、Br-、NO3-、PO43-、SO32-、SO42-)的测定 离子色谱法》[6]对岩溶地下水中硝酸根的含量进行测定，采用不确定度连续传递模式[7]对其测量过程中产生的不确定度进行计算评估.

在校准曲线拟合这一关键步骤上，考虑到各个标准点的分析误差对校准曲线的影响，本文采用不同的回归方式对校准曲线进行拟合回归并得到相应的不确定度评定结果. 其中，以x、y相对差为权重进行双误差曲线回归得到的不确定度评定模型，与传统的简单直线回归方式[8-9]相比较，结果更加准确和可靠.

1 试验部分

1.1 仪器与试剂

仪器：861型离子色谱仪(瑞士万通)，配置有MetroSep A Supp 5-150分离柱.

硝酸钾(基准级)、碳酸钠(优级纯)、碳酸氢钠(优级纯)均购置于广州化学试剂厂.

电子天平：梅特勒-托利多，型号为XS205，产地为瑞士.

1.2 溶液制备

硝酸根标准储备溶液：ρ0(NO3-)=1 000 mg/L，准确称取硝酸钾(KNO3，基准级，纯度99.96%，预先在100 ℃下烘至恒重) 1.630 5 g于烧杯中，用水溶解后定容至1 000 mL容量瓶中，混匀.

硝酸根标准使用液：ρ1(NO3-)=100 mg/L，用单标线吸量管移取25 mL硝酸根标准储备液于250 mL容量瓶中，用水定容后混匀.

Na2CO3和NaHCO3均为优级纯，试验用水为去离子水(电阻率大于18 MΩ·cm).

1.3 检测

色谱条件：淋洗液为3.2 mmol/L Na2CO3+1.0 mmol/L NaHCO3混合液(预先经0.22 μm滤膜过滤)，洗脱方式为等度洗脱，柱温35 ℃，流速0.7 mL/min，进样体积100 μL. 按上述工作条件将仪器调试完毕，待基线稳定后，对硝酸根标准溶液和样品进行测定.

分别加入1.00、2.00、5.00、10.00、15.00 mL硝酸根标准使用液至100 mL容量瓶中，用水定容后混匀，配制成硝酸根质量浓度分别为1.0、2.0、5.0、10.0、15.0 mg/L的标准系列溶液，按仪器工作条件测定其响应值. 以标准系列溶液浓度对应仪器响应值，绘制硝酸根校准曲线.

水样经0.22 μm滤膜过滤后直接进离子色谱仪测定其硝酸根含量.

2 不确定度的评定

2.1 硝酸根标准储备液的配制及不确定度

硝酸根标准储备液的配制：

(1)

式中：ρ0—硝酸根标准储备液质量浓度(mg/L)；φ为KNO3换算为NO3-的系数；P—KNO3纯度；m0—KNO3质量(g)；V—定容体积(L).

硝酸根标准储备液浓度的不确定度主要来源于KNO3纯度的不确定度、称量的不确定度和定容体积的不确定度. 根据不确定度传播律，ρ0的合成标准不确定度为：

(2)

2.1.1 KNO3纯度的不确定度u(P)

2.1.2 称量的不确定度u(m0)

2.1.3 定容体积的不确定度u(V)

定容体积1 000 mL引入的不确定度主要包括：容量瓶允差引入的体积不确定度u(V1)、估读误差引入的体积不确定度u(V2)(即重复性不确定度)和实验室环境温度变化所导致的容量瓶内溶液体积变化引入的不确定度u(V3).

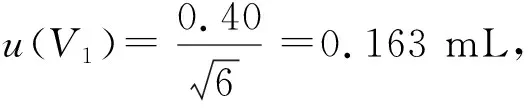
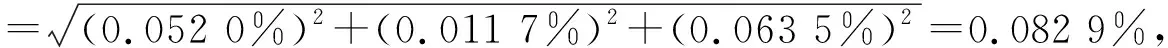
2.2 硝酸根标准使用液的配制及不确定度

硝酸根标准使用液的配制：

(3)

式中：ρ1—硝酸根标准使用液的质量浓度(mg/L)；ρ0—硝酸根标准储备液的质量浓度(mg/L)；V0—移取硝酸根标准储备液的体积(mL)；V1—定容体积(mL).

硝酸根标准使用液浓度的不确定度主要来源于硝酸根标准储备液浓度的不确定度、移取硝酸根标准储备液体积的不确定度以及定容体积的不确定度.

根据JJG 196-2006，以下常见玻璃器皿的体积(V)的不确定度如表1所列.

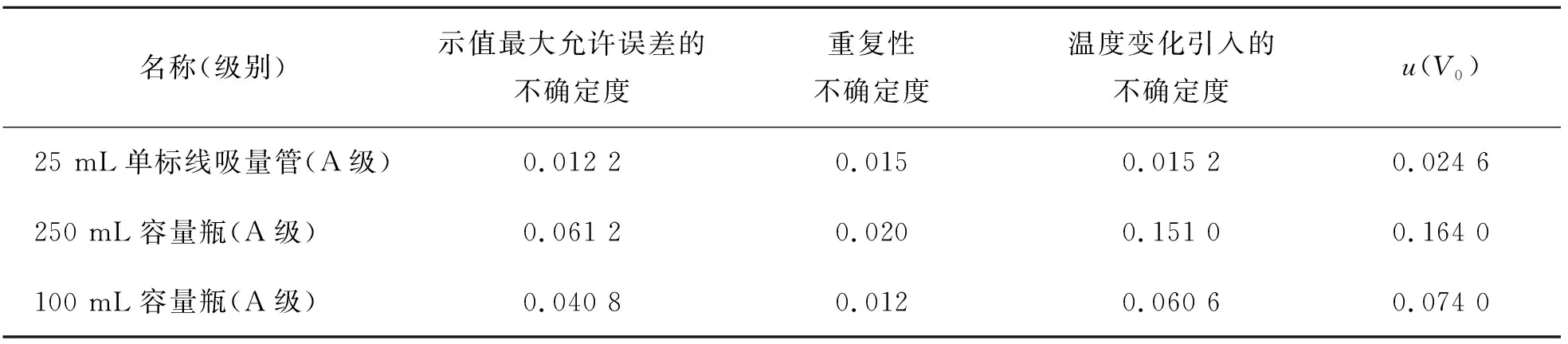
表1 常见玻璃器皿体积的不确定度Table 1 Uncertainty of common glassware volume mL

2.2.1 硝酸根标准储备液浓度ρ0的不确定度u(ρ0)

由2.1节评定结果得到：ur(ρ0)=0.082 9%

2.2.2 移取硝酸根标准储备液体积V0的不确定度u(V0)

2.2.3 定容体积V1的不确定度

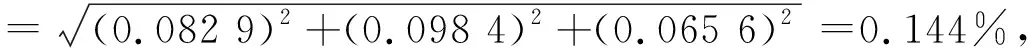
2.3 硝酸根标准系列溶液的不确定度

硝酸根标准系列溶液配制如下：分别用5 mL刻度移液管(A级)移取1.00、2.00、5.00 mL，用10 mL刻度移液管(A级)移取10.00 mL，用25 mL刻度移液管(A级)移取15.00 mL，配制的标准系列各点硝酸根溶液浓度分别为1.0、2.0、5.0、10.0、15.0 mg/L.

其数学模型为：

(4)

式中：ρi—标准系列各点的质量浓度(mg/L)；ρ1—硝酸根标准使用液的质量浓度(mg/L)；Vi—标准系列各点移取标准使用液的体积(mL)；V—标准系列各点的定容体积(100 mL).

根据不确定度传播律，硝酸根标准系列溶液浓度的合成标准不确定度为：

首先，硝酸根标准使用液浓度ρ1的标准不确定度为：ur(ρ1)=0.144%.

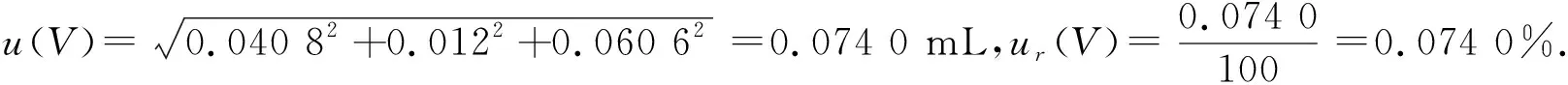
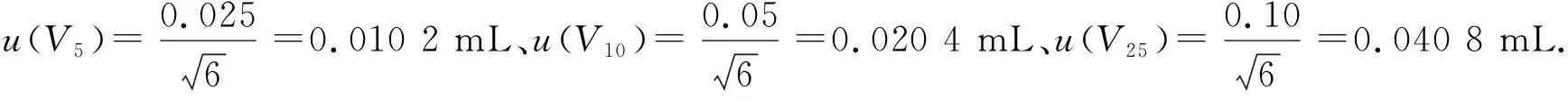
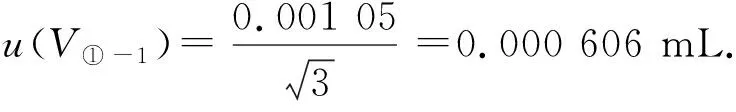
所以，u(ρ①)=1.59%×1.0=0.015 9 mg/L.

同上计算可得：硝酸根标准系列溶液各质量浓度(从低到高)的标准不确定度分别为0.015 9、0.016 1、0.017 9、0.036 5、0.069 6 mg/L.

2.4 仪器测量产生的不确定度

按照仪器色谱条件测定硝酸根标准溶液的响应值，对各标准点重复测定5次，测量数据及统计结果如表2所列.

表2 硝酸根标准溶液的仪器测量数据及统计Table 2 Measurement data of nitrate standard solutions and statistical results

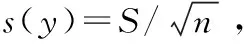
2.5 不同回归方式下的回归值和回归残差

对硝酸根标准溶液各点进行5次测定，得到各标准点响应值的平均值及该值的测量标准不确定度(即yi±s(yi))，具体数据如表2所列. 根据表2的数据进行线性拟合，得到校准曲线的拟合方程y=f(x). 常用的拟合方式有简单直线方程拟合、以x、y的相对误差为权重的双误差直线方程拟合、二次曲线方程拟合以及三次曲线方程拟合，通过回归计算，各校准曲线下拟合回归得到的结果如表3所列.

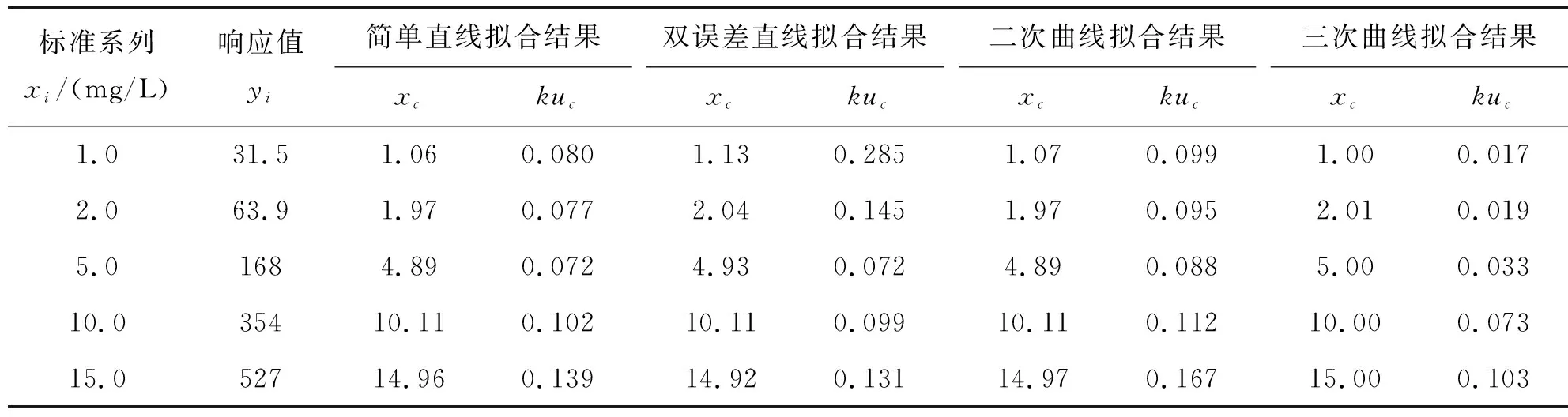
表3 不同回归方式下得到的扩展不确定度(k·dx)Table 3 Expanded uncertainty results evaluated with different regression methods

从表3可以看出，目前在实验室广泛被采用的一次线性回归得到的扩展不确定度与双误差拟合回归得到的扩展不确定度在校准曲线中间点和高点是较为接近的. 但在低点处明显要优于双误差回归得到的结果，显然这是欠合理的，这同时也证明了实验室目前常用的不确定度计算方法存在不足之处.

而二次曲线和三次曲线拟合回归得到的结果与简单直线拟合回归得到的结果相类似，甚至在低点处还要优于简单直线拟合回归，因此按其计算不确定度亦存在不足之处.

根据试验经验可知，对低含量被测物进行分析时，在接近方法检出限时其测定结果的误差会成倍放大，而上述双误差直线加权拟合的方法较好地体现了这一点，与实际测定情况相吻合.

2.6 双误差拟合回归合成的扩展不确定度

对于上述任一测量点，以x、y相对差为权重进行双误差曲线回归，其合成标准不确定度可由下式计算[12]：

(5)

若包含因子为k，则结果为：xc±k·uc(x) (k=2，包含概率约为95%).

需要说明的是：(1)上述计算过程忽略了元素K、N和O的原子量误差所带来的不确定度；(2)由于空白溶液在该检测灵敏度下未检出，因此未讨论空白溶液的不确定度.

3 实际样品的测定及不确定度评定

选取经过滤的待测水样1#和2#，按照仪器色谱条件测定后其响应值如表4所列.

表4 实际水样分析Table 4 Analytical results of karst underground water samples

*：线性插值法计算值

若取包含因子k=2，则1#和2#水样的硝酸根质量浓度分别为：(3.93±0.18)、(2.58±0.22) mg/L. 对于结果中的扩展不确定度，其中由标准溶液配制引入的不确定度占总的不确定度分别为4.62%和2.21%，样品测试引入的不确定度占总的不确定度分别为6.89%和1.33%，曲线拟合及计算所引入的不确定度占总的不确定度分别为88.49%和96.47%.

4 结论

(1)在不确定度评定过程中，不论是以何种校准曲线回归方式来拟合，主要的不确定度来自校准曲线本身的拟合过程. (2)以x、y的相对差为权重的双误差曲线回归方式，统筹考虑了校准曲线每个标准点的分析误差对拟合曲线的影响，获得了更加准确可靠的不确定度评定模型. (3)计算结果表明，当水样中硝酸根含量越低，校准曲线拟合过程所引入的不确定度对总不确定度贡献较大. 因此实际测定过程中要选择一条合适的校准曲线进行定量分析.