浸润数学文化 从容应对复习课——以阿波罗尼斯圆性质及其应用为例

金诗梦

温州市瓯海区第一高级中学 浙江温州 325000

背景展示阿波罗尼斯是古希腊著名数学家，与欧几里得、阿基米德被称为亚历山大时期数学三巨匠，他对圆锥曲线有深刻而系统的研究，主要研究成果集中在他的代表作《圆锥曲线》一书，阿波罗尼斯圆是他的研究成果之一。

（人教A版124页B组第3题）已知点M与两个定点O(0,0),A(3,0)点距离的比为，求点的轨迹方程。

（人教A版144页B组第2题）已知点M与两个定点M1，M2距离的比是一个正数m,求点M的轨迹方程，并说明轨迹是什么图形（考虑m=1=1和m≠1两种情形）。

公元前3世纪，古希腊数学家阿波罗尼斯(Apollonius)在《平面轨迹》一书中，曾研究了众多的平面轨迹问题，其中有如下著名结果：到平面上两定点距离比等于定值的动点轨迹为直线或圆．（定值为1时是直线，定值不是1时为圆）

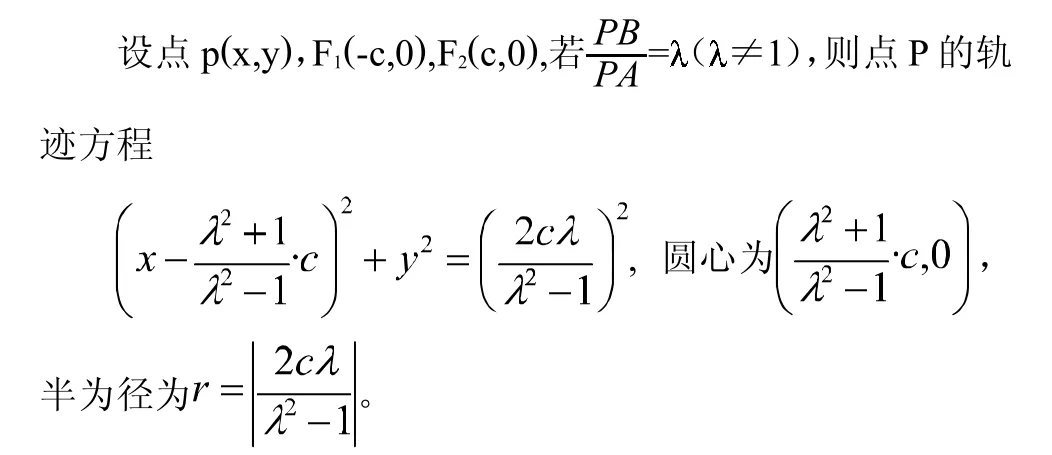
定义：一般的平面内到两顶点A，B距离之比为常数（≠1）的点的轨迹为圆，此圆称为阿波罗尼斯圆

类型一：求轨迹方程

1.已知点 M 与两个定点 O（0，0），A（3，0）的距离的比为，求点M的轨迹方程

3（.2006年高考四川卷第6题）已知两定点A（-2，0），B（1，0），如果动点P满足条件|PA|=2|PB|，则点P的轨迹所包围的图形面积等于（ ）

A． B.4 C.8 D.9

类型二：求三角形面积的最值

5.（2011浙江温州高三模拟）在等腰中，AB=AC，D为AC的中点，BD=3，则ABC面积的最大值为

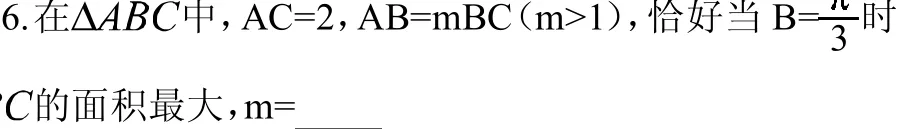
类型三：定点定值问题

类型四：阿波罗尼斯圆的性质

类型五：阿波罗尼斯圆的应用