A Size-Dependent Functionally Graded Higher Order Plate Analysis Based on Modified Couple Stress Theory and Moving Kriging Meshfree Method

2018-12-26TranChienThaiandNguyenXuan

Computers Materials&Continua 2018年12期

T.D.Tran,Chien H.Thai and H.Nguyen-Xuan

1 Faculty of Construction & Electricity,Ho Chi Minh City Open University,Ho Chi Minh City,Vietnam.

2 Division of Computational Mechanics,Ton Duc Thang University,Ho Chi Minh City,Vietnam.

3 Faculty of Civil Engineering,Ton Duc Thang University,Ho Chi Minh City,Vietnam.

4 Center for Interdisciplinary Research in Technology,Ho Chi Minh City University of Technology(HUTECH),Ho Chi Minh City,Vietnam.

5 Department of Physical Therapy,Graduate Institute of Rehabilitation Science,China Medical University,Taichung,40402,Taiwan.

Abstract:A size-dependent computational approach for bending,free vibration and buckling analyses of isotropic and sandwich functionally graded(FG)microplates is in this study presented.We consider both shear deformation and small scale effects through the generalized higher order shear deformation theory and modified couple stress theory(MCST).The present model only retains a single material length scale parameter for capturing properly size effects.A rule of mixture is used to model material properties varying through the thickness of plates.The principle of virtual work is used to derive the discrete system equations which are approximated by moving Κriging interpolation(MΚI)meshfree method.Numerical examples consider the inclusions of geometrical parameters,volume fraction,boundary conditions and material length scale parameter.Reliability and effectiveness of the present method are confirmed through numerical results.

Keywords:Modified couple stress theory,isotropic and sandwich FGM plates,moving Κriging meshfree method.

1 Introduction

Nowadays,devices with small size have been widely used in various fields of aerospace,machinery,electronics and medical equipment.They have been also known as microelectro-mechanical systems(MEMS)devices and are made of microbeam and microplate structures.Therefore,to use the devices effectively,an insight into mechanical behaviors of micro-structures are required.In addition,experimental studies indicate that the size effect takes into account in the micro-structures [Lam,Yang,Chong et al.(2003)].Unfortunately,the classical continuum theories cannot enable to forecast exactly behaviors of micro-structures because of the insufficiency of material length scale parameters.Therefore,the advanced theories accounting higher order strain gradients named as the strain gradient theories taking into accounts additional material length scale parameters have been developed.

The strain gradient theories in the literature can be primarily categorized by two groups:The general strain gradient theory and the couple stress theory.The first one known as the general strain gradient theory proposed by Mindlin et al.[Mindlin and Eshel(1968);Mindlin(1964)],which are examined by all strain gradient components.This theory takes five material length-scale parameters into account in the classical material constants.However,it is hard to use in modeling and computation.For simplicity,the second theory[Toupin(1962); Mindlin and Tiersten(1962); Κoiter(1964)] considered an antisymmetric part of the strain gradient and included two material length scale parameters.In particular,a modified version of this theory known as the modified couple stress theory(MCST)was proposed by Yang et al.[Yang,Chong,Lam et al.(2002)].It only involves a symmetric rotation gradient component and one material length scale parameter.At present,the MCST is highly interested in research community.

The MCST has been applied to FG microplates.A size-dependent three-dimensional(3D)elasticity model was early developed by Salehipour et al.[Salehipour,Nahvi,Shahidi et al.(2017)] for bending analysis of FG microplates.Guo et al.[Guo,Chen and Pan(2016);Guo,Chen and Pan(2017)] extended this approach to multilayered microplates.However,it is in fact for plate analysis that the size-dependent 3D elasticity model shows computationally too expensive.Tsiatas [Tsiatas(2009)] proposed then the Κirchhoff plate model for bending analysis of isotropic microplates.Several solutions based on this plate model were reported in Yin et al.[Yin,Qian,Wang et al.(2010); Jomehzadeh,Noori and Saidi(2011); Ansari and Norouzzadeh(2016)].After that,a size-dependent first-order shear deformation plate theory(FSDT)based on the MCST was developed by Ma et al.[Ma,Gao and Reddy(2011)] for bending analysis and Κe et al.[Κe,Wang,Yang et al.(2012)] for free vibration analysis of isotropic microplates.Other relevant researches to this approach were also presented by Zhou et al.[Zhou and Gao(2014)] and Alinaghizadeh et al.[Alinaghizadeh,Shariati and Fish(2017)].Moreover,a sizedependent third-order shear deformation(TSDT)model combined with the MSCT was developed by Gao et al.[Gao,Huang and Reddy(2013)] for isotropic microplates.After that,it was extended for FG microplates by Thai et al.[Thai and Κim(2013)] and Eshraghi et al.[Eshraghi,Dag and Soltani(2016)].Thai et al.[Thai and Vo(2013)]proposed the sinusoidal plate model based on the MCST for FG microplates.Similarly,He et al.[He,Lou,Zhang et al.(2015)] and Lou et al.[Lou,He and Du(2015)] presented a size-dependent refined higher-order shear deformation(RPT)model for FG microplates.A size-dependent model accounting all shear and normal strains so-called the quasi-3D shear deformation theory was also proposed by Κim et al.[Κim and Reddy(2013)] for behavior analysis of FG microplates.The FSDT model was further developed for analysis of FG microplates [Lei,He,Zhang et al.(2015); Trinh,Vo,Thai et al.(2017);Nguyen,Nguyen,Wahab et al.(2017)].

For more details,Thai et al.[Thai,Vo,Nguyen et al.(2017)] presented a review of continuum mechanics models for size-dependent analysis of beams and plates.It showed that most size-dependent models developed rapidly in the last five years and computational approaches herein were almost concerned with analytical methods.Addressing attempts to the advanced development of numerical methods such as finite elements,isogeometric analysis and meshfree for size-dependent analysis,we review a list of several studies in the literature.Phadikar et al.[Phadikar and Pradhan(2010)]presented a Κirchhoff finite element model based on the nonlocal elasticity theory for nanoplates.A FSDT finite element model combined with the nonlocal elasticity theory was reported by Ansari et al.[Ansari,Rajabiehfard and Arash(2010)].Natarajan et al.[Natarajan,Chakraborty,Thangavel et al.(2012)] proposed a size-depedent isogeometric Mindlin plate model based on the nonlocal elasticity theory for nanoplates.Similarly,Nguyen et al.[Nguyen,Hui,Lee et al.(2015)] developed a size-dependent quasi-3D shear deformation model based on the nonlocal elasticity theory for FG nanoplates.An improved model by a combination of nonlocal and surface effects based on IGA was presented by Ansari et al.[Ansari and Norouzzadeh(2016)].Besides,a size-dependent isogeometric model based on the modified strain gradient theory was proposed by Thai et al.[Thai,Ferreira and Nguyen(2018)] for analysis of FG microplates.Foroushani et al.[Sarrami-Foroushani and Azhari(2016)] and Mirsalehi et al.[Mirsalehi,Azhari and Amoushahi(2015)] developed the finite strip method incorporate with the nonlocal elasticity theory for FG nanoplates.Moreover,a size-dependent meshfree model based on the MCST for the isotropic microplates was developed by Roque et al.[Roque,Ferreira,and Reddy(2013)].This model was applied for the FG microplates by Thai et al.[Thai,Ferreira,Lee et al.(2018)].A further development of the meshfree method based on the nonlocal elasticity theory was presented by Zhang et al.[Zhang,Lei,Zhang et al.(2015)]for analysis of nanoplates.From above studies,it is clearly that a number of articles found in the literature based on the numerical solutions are still limited for analysis of micro/nano plates and shells [Rabczuk,Gracie,Song et al.(2010); Rabczuk,Areias and Belytschko(2007); Zenkour(2005)].The above mention motivates us to develop a sizedependent HSDT meshfree model combined with the MCST for bending,free vibration and linear buckling analyses of isotropic and sandwich FG microplates.

The paper is outlined as follows.Basic equations of FG microplate based on the MCST are summarized in Section 2.In Section 3,FG microplate formulations based on moving Κriging interpolation are introduced.Numerical results are illustrated in Section 4.Finally,concluding remarks are given in Section 5.

2 Basic equations

2.1 Problem description

2.1.1 Isotropic FG plates

As shown in Fig.1,a FG microplate with thickness h made of a mixture of ceramic and metal is considered.Effective material parameters of the FG microplates as Young’s modulus(E),Poisson’s ratio(v)and density mass(ρ)can be computed by a rule of mixture as:

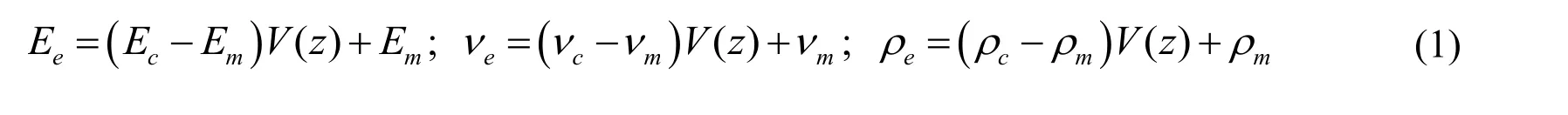
where the subscripts c and m define the ceramic and metal,respectively.V(z)is the volume fraction of the constituents through the thickness by Reddy [Reddy(2000)]:

in which the subscript n is the volume fraction exponent or the power index.

Figure 1:A typical configuration of FG microplate.

2.1.2 Sandwich plates

A sandwich FG microplate(cf.Fig.2)made of a combination of an isotropic core and two FGM face sheets is considered,in which the bottom and top FGM sheets change from the metal-rich surface(z= z1)to the ceramic-rich surface(z= z2)and the ceramicrich surface(z= z3)to the metal-rich surface(z= z4),respectively.The volume fraction of two face sheets are formed by a power-law function through the plate thickness given by Zenkour et al.[Zenkour(2005); Li,Lu and Κou(2008)]:

Several types of the bottom-core-top thickness ratio(hb-hc-ht)are examined in this work.For example,hb-hc-ht=2-1-2indicates that the thickness of two face sheets are greater than two times compared to the core.

Figure 2:The sandwich plate with FGM sheets and homogeneous core

2.2 Modified couple stress theory

The modified couple stress theory(MCST)[Yang,Chong,Lam et al.(2002)] regards one additional material length scale parameter in addition to the classical material constants instead of two ones as in the classical couple stress theory.The MCST additionally considers the symmetric rotation gradient tensor χinto the strain tensor ε.According to the MCST,the virtual strain energy U in an isotropic linearly elastic material can be described by:

where σis the Cauchy stress tensor; mis high-order stress tensor corresponding with the rotation gradient tensors χ,respectively.

The relations of the strain tensor with displacement vector u =｛u vw｝Tand the rotation gradient tensor with rotation vector θ=｛θxθyθz｝Tare defined by

The relation between displacement vector u and rotation vector θis expressed as follows

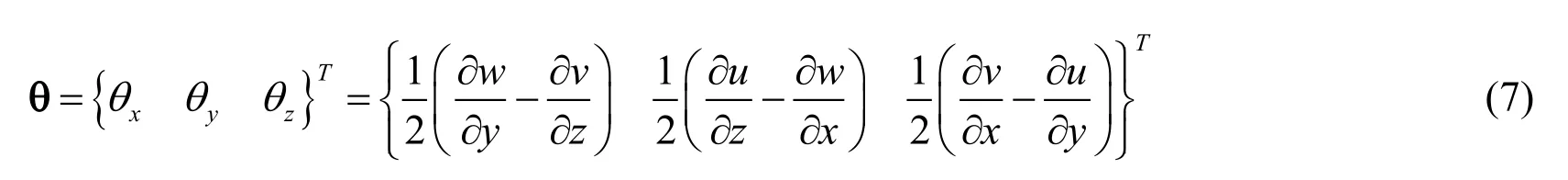
The constitutive relations are given by

where C,G,are the stiffness tensor or elasticity tensor,the shear module and the material length scale parameter,respectively.

2.3 Kinematics of FG microplates

where

in which u0,v0,w0,βxand βyare the in-plane,transverse displacements and the rotation components in the y-z,x-z planes,respectively.The symbols ‘,x’and ‘,y’indicates the derivative of arbitrary functions following x and y directions,respectively,and f(z)is a certain function defined through plate thick.

Substituting Eq.(10)into Eq.(5),the strain components can be obtained by

The strains can be decomposed into two terms consisting of bending and shear strains which are expressed as follows

where

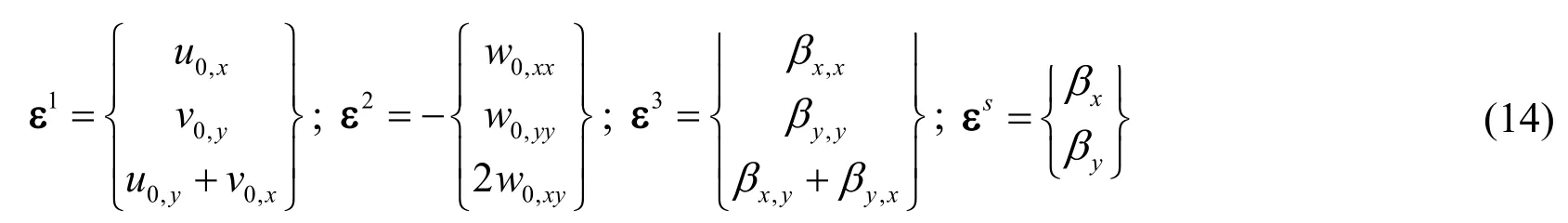
in which f′(z)is the derivation of the function f(z).The function f(z)can be determined so that transverse shear stresses corresponding with shear strains in Eq.(13)at top and bottom of microplates are equal to zeros or the value of its tangential at z = ±h/2is equal to zero.

Substituting Eq.(10)into Eq.(7),the rotation vector becomes

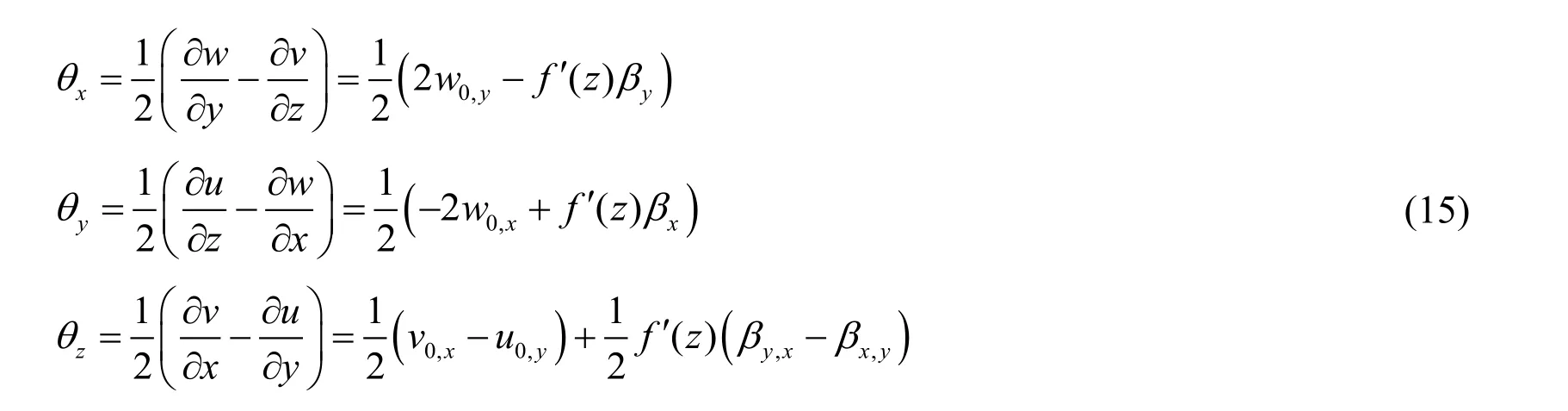
Substituting Eq.(15)into Eq.(6),we write the symmetric rotation gradient as follows:

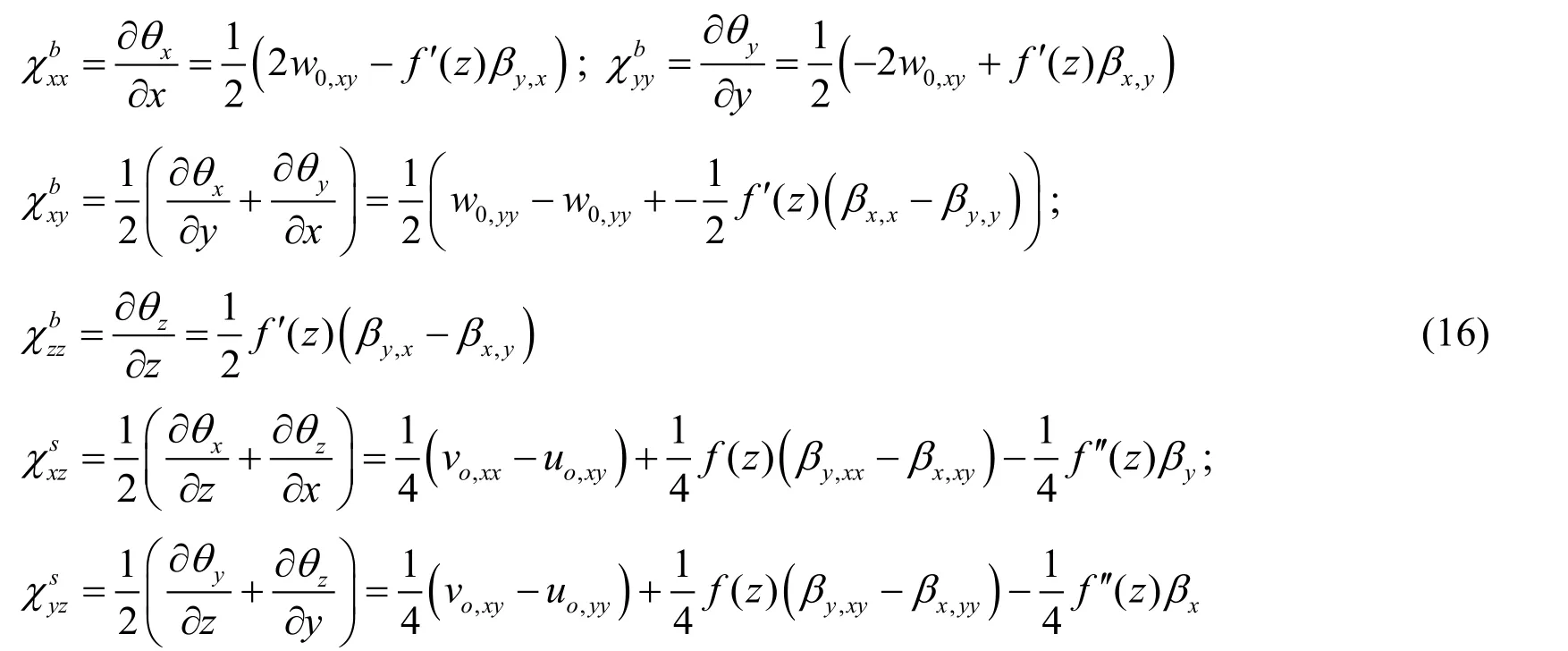
The symmetric rotation gradient tensor can be rewritten under a compact form by

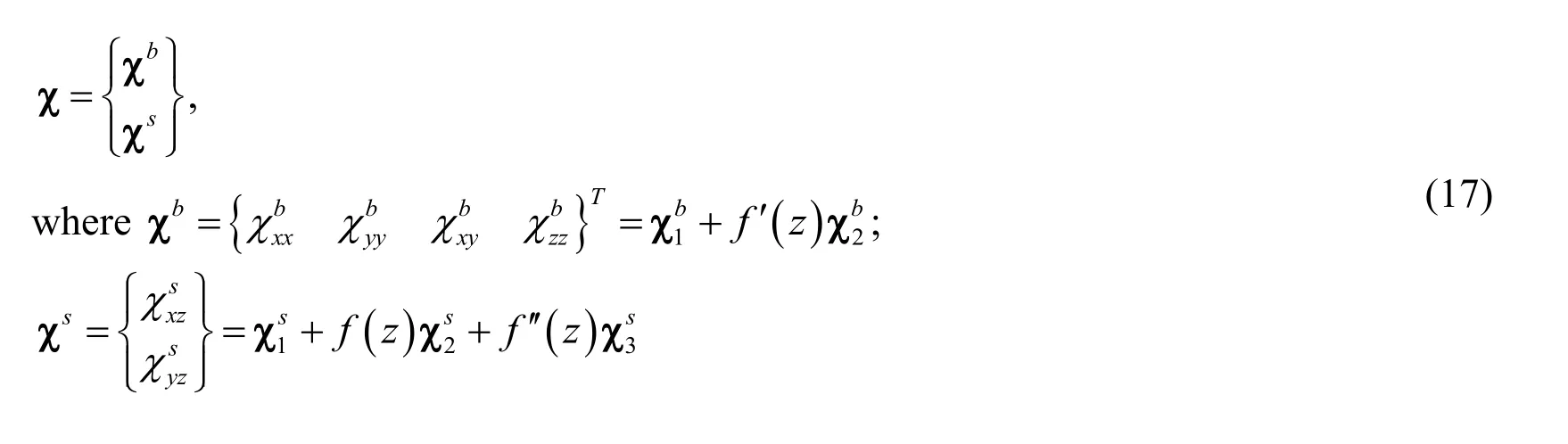
and

The classical and modified couple stress linear elastic constitutive relations are written as follows

where

where Eeand νeare the effective Young module and Poisson’s ratio according to Eq.(1),respectively.

The discrete Galerkin weak form for the bending analysis of the FG microplate subjected to a transverse loading q0are written by

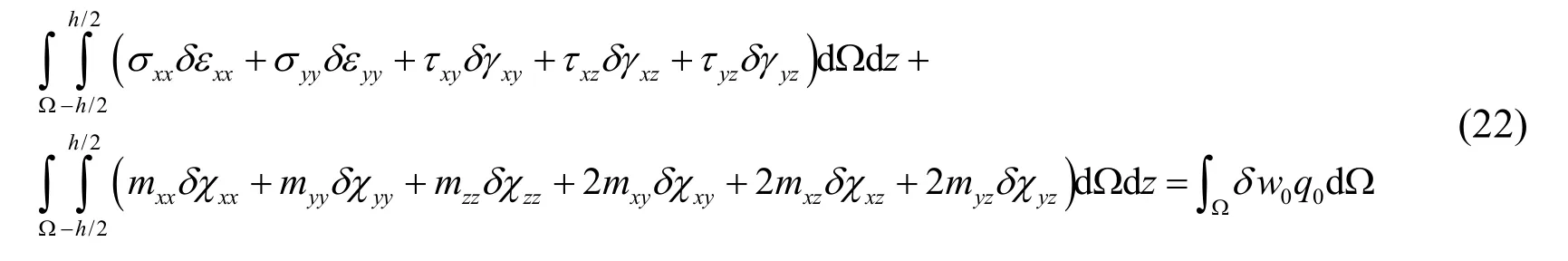
The Eq.(22)can split into two independent integrals following to middle surface and zaxis direction.Substituting Eq.(19)and Eq.(20)into Eq.(22),the discrete Galerkin weak form can be rewritten under the matrix form as follows

where

in which

in which I2x2,I4x4are identity matrices of size 2×2 and 4×4,respectively.

The discrete Galerkin weak form for free vibration analysis of the FG microplate can also be defined by:

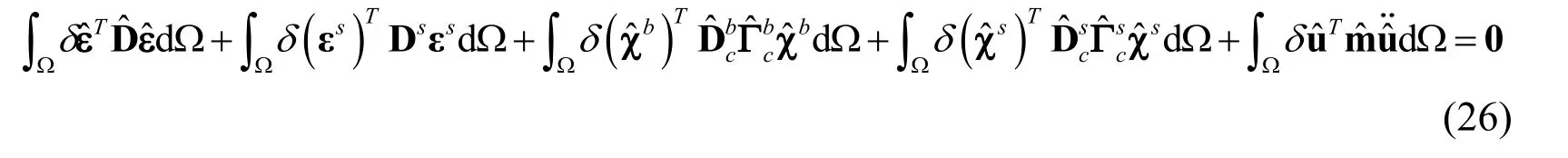
where

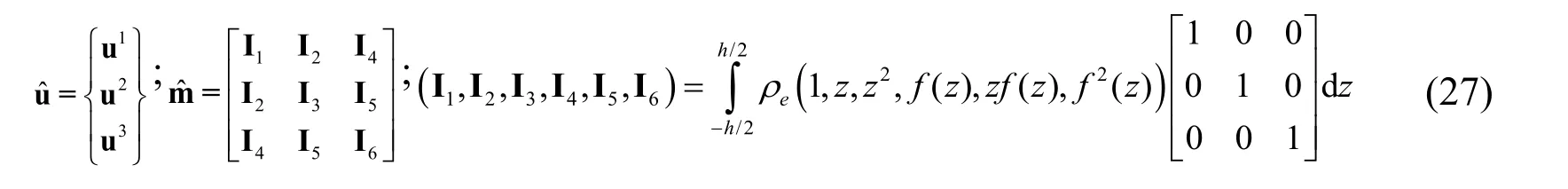
The discrete Galerkin weak form for buckling analysis of the FG microplate under an inplane loading can be expressed by:

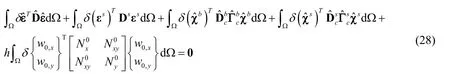
3 FG microplate formulation based on moving Kriging interpolation

3.1 Moving Kriging interpolation shape functions

Let us consider a given domain Ωwhich is discretized into a set of nodes xI(I = 1,...,NP),as shown in Fig.3,in which NP denotes the number of nodes in the problem domain.According to the moving Κriging shape functions,the displacement field uh(x)is described by

where uIis the unknown coefficient associated with node I and NIis the moving Κriging shape function being expressed as follows

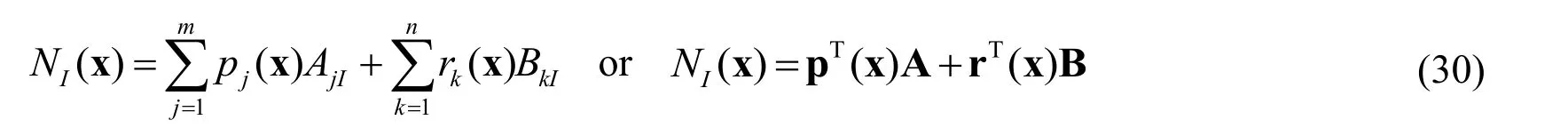
in which n is a number of nodes in a support domain Ωx∈Ωand m is the dimension of a polynomial basis function space.In addition,A ,B ,p(x)and r(x)are expressed as:

where I is the identity matrix of size n × n.

According to the discrete Galerkin weak form,a minimum choice of p(x)is the quadratic polynomial functions:

Now we write P and R as follows

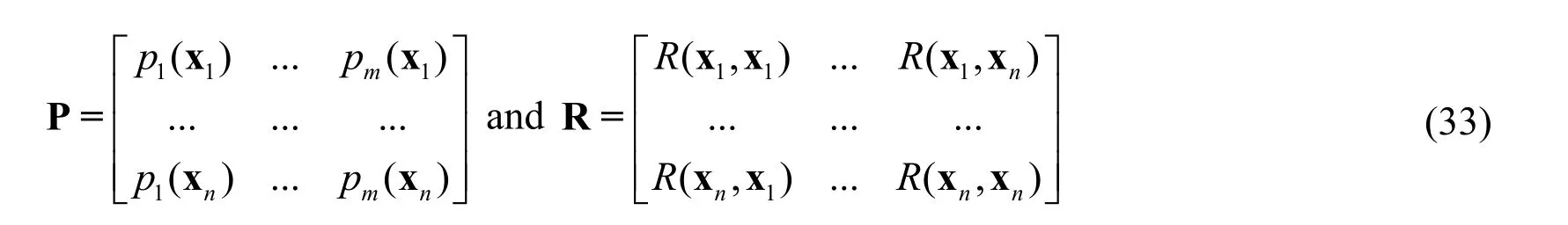
Various correlation functions consisting of multi-quadrics,thin plate splines,Gaussian can be chosen to construct MΚI shape functions.For example,the Gaussian function can be utilized and it is defined as

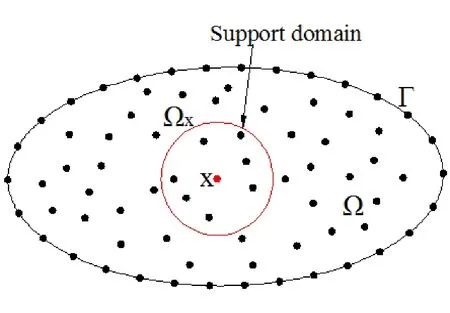
Figure 3:Domain representation and support domain of 2D model

The first and second-order derivatives of the MΚI shape functions are expressed by

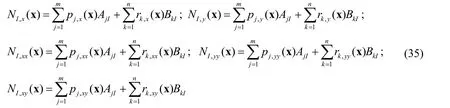
In meshfree methods,a support domain of nodes is needed to construct the shape functions.Herein,the size of the support domain is important and can be defined as

where dcand αare an average distance between nodes and a scale factor,respectively.It is shown that the size of the support domain is enough large to support a sufficient number of nodes for achievement of stable solutions.Such a value of scale factor can be determined through numerical experience.

3.2 A MKI-based formulation using the HSDT and modified couple stress theory

According to the MΚ interpolation,the displacement field can be approximated as

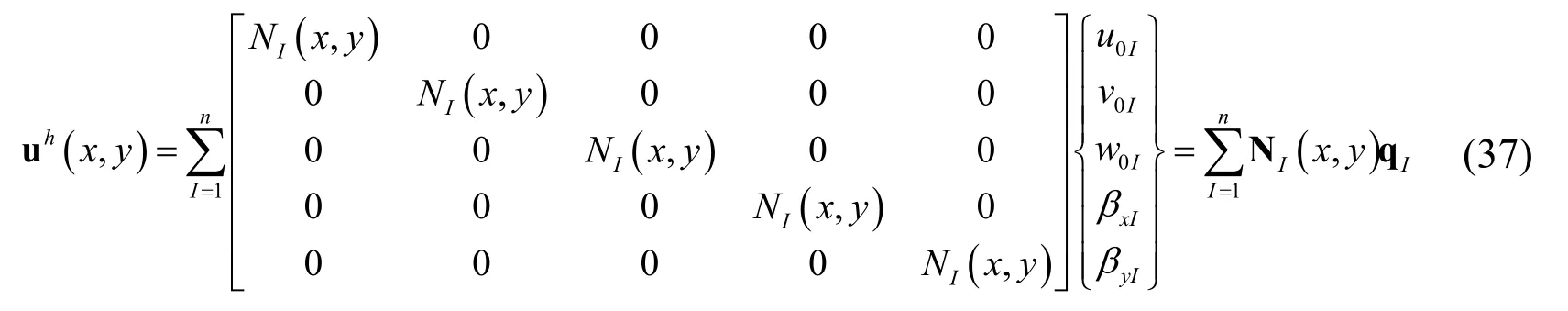
where qI=｛u0Iv0Iw0IβxIβyI｝Tis a vector that contains degrees of freedom of node I.

Substituting Eq.(36)into Eq.(14),the strain components can be rewritten as

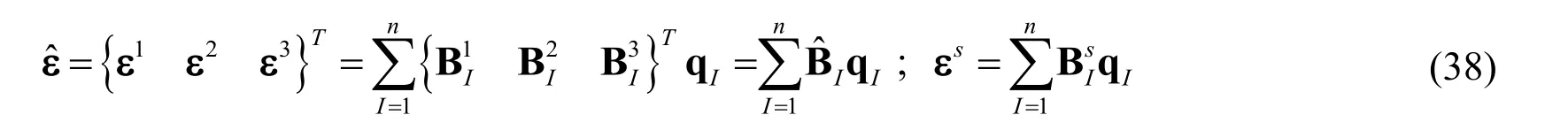
in which,

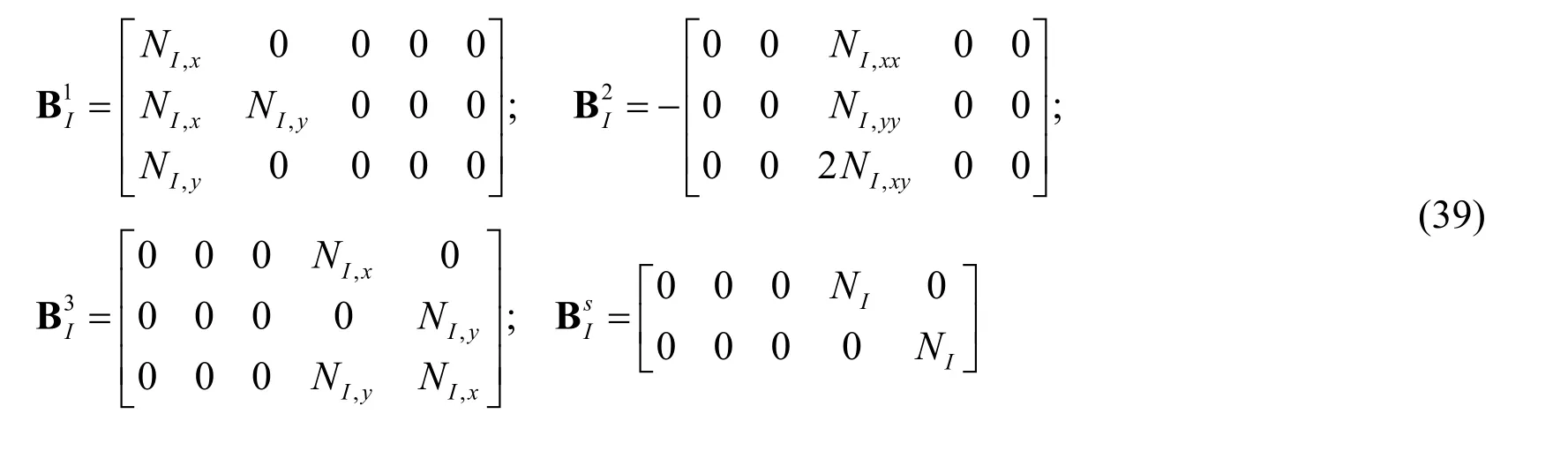
Similarly,the rotation gradient components are obtained by substituting Eq.(36)into Eq.(18)as follows

in which,

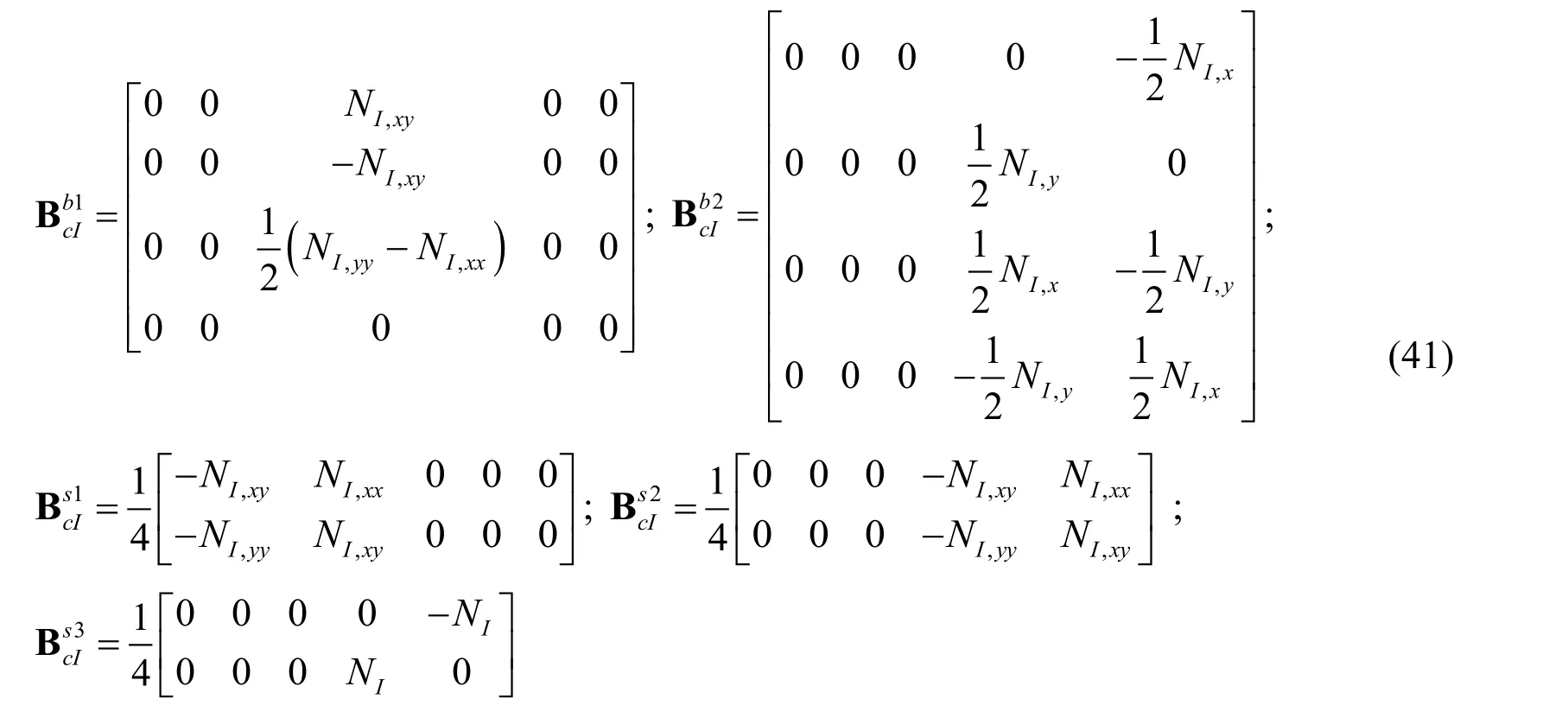
Substituting Eq.(36)into Eq.(11),the displacement fields u1,u2and u3can be expressed as follows

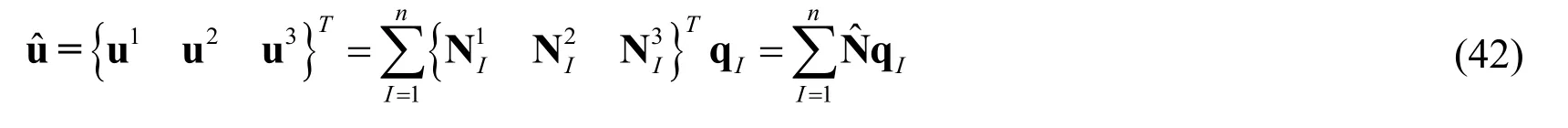
where

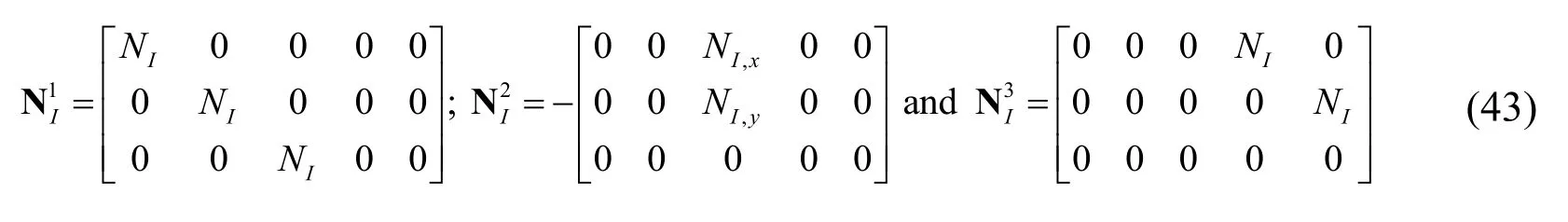
The derivatives of transverse bending and shear displacements are also given by

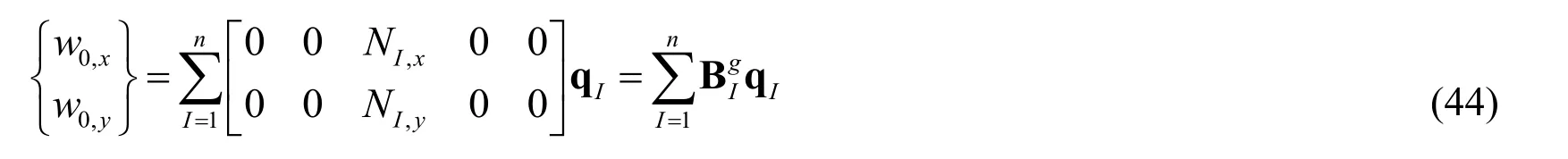
Substituting Eqs.(37),(39),(41)and(43)into Eqs.(23),(26)and(27),we obtain the equations system of the static,free vibration and buckling analyses of FG microplates as

where K(K =Kε+Kθ),M ,Kgand Fare the global stiffness matrix,mass matrix,geometry stiffness matrix and force vector,respectively,in which:

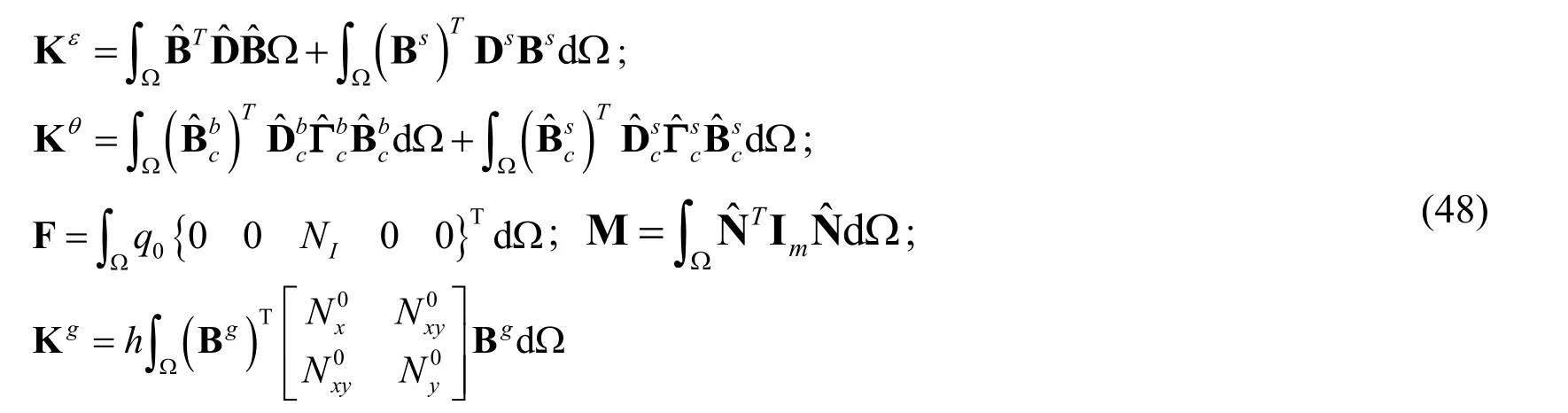
and ωand λcrin Eq.(45)and Eq.(46)are the natural frequency and the critical buckling load,respectively.

4 Numerical examples and discussions

To start with numerical analysis,material properties are given in Tab.1.Without loss of generality,the cubic distribution function [Reddy(2000)] is used.In addition,a background cell with 4×4 Gauss points for each cell is used for numerical computation.The material length scale factor(l=17.6×10-6m)[Lam,Yang,Chong et al.(2003)] is adopted in numerical examples.Also,homogeneous Dirichlet boundary conditions(BCs)are considered as follows:

● Simply supported:

▪ Rectangular plate

▪ Circular plate

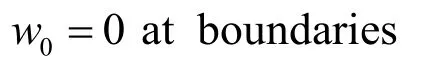
● Fully clamped:

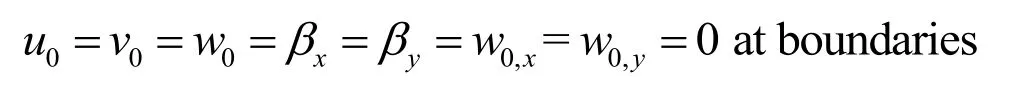
The BCs for u0,v0,w0,βx,βyare enforced as the similar way to the traditional finite element method,while the derivation of displacements w0,x,w0,yis eliminated by assigning zero values of the transverse and shear displacements at boundary nodes and its adjacent nodes as same as the previous studies [Nguyen,Ngo and Nguyen-Xuan(2017);Nguyen-Thanh,Zhou,Zhuang et al.(2017)].In addition,the essential boundary conditions for the derivation of transverse and shear displacements into the MΚ meshfree method are simply implemented without use of any additional variables.

For comparison purpose,non-dimensional displacement,natural frequency and critical buckling load of the FG microplate are defined by:

● The isotropic FG rectangular microplate:

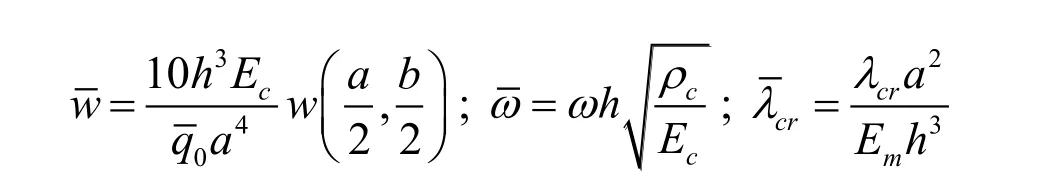
● The sandwich FG rectangular microplate:

● The isotropic FG circular microplate:

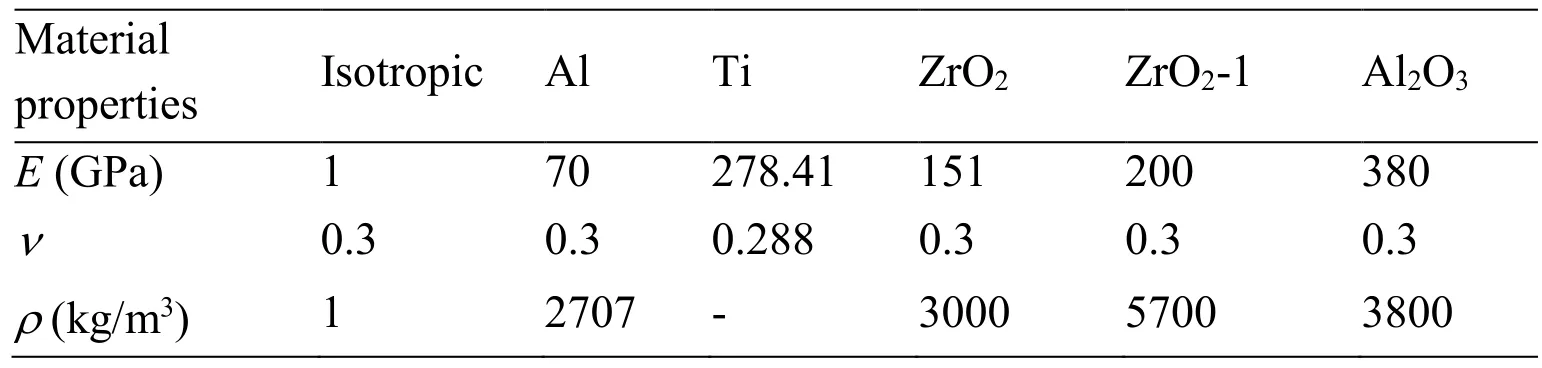
Table 1:Material properties

4.1 Static analysis

4.1.1 Study of convergence

Let us consider an isotropic simply supported square microplate subjected to a sinusoidally distributed loadThe length-to-thickness ratio is taken equal 20(a/h=20).Several values of material length scale-to-thickness ratio(l/h=0,0.2,0.6,1)are employed.The square microplate is modeled by 11×11,17×17,23×23 and 31×31 nodes as illustrated in Fig.4.In addition,we consider the influence of the scale factor on the underlying solution.The convergence of the non-dimensional displacement of HSDT meshfree model is given in Tab.2.The results obtained are compared with those reported by Thai et al.[Thai and Κim(2013)] based on a TSDT analytical model(Anal)and Nguyen et al.[Nguyen,Nguyen,Wahab et al.(2017)] based on a RPT isogeometric analysis(IGA)model.The percentage error(%)of displacement between the present and analytical solutions is given in parenthesis.We see that the present solution converges well to the analytical solution when increasing a number of nodes as well as the scale factor.Also,the increase of the material length scale-to-thickness ratio l/h results in the decrease of the non-dimensional displacement.Hence,the stiffness of isotropic microplate increases when taking into account size-dependent effect.From Tab.2,it can be seen that the present solution is in very good agreement with the reference solution at the value α=2.6.Therefore,this scale factor value can be used for other next examples.

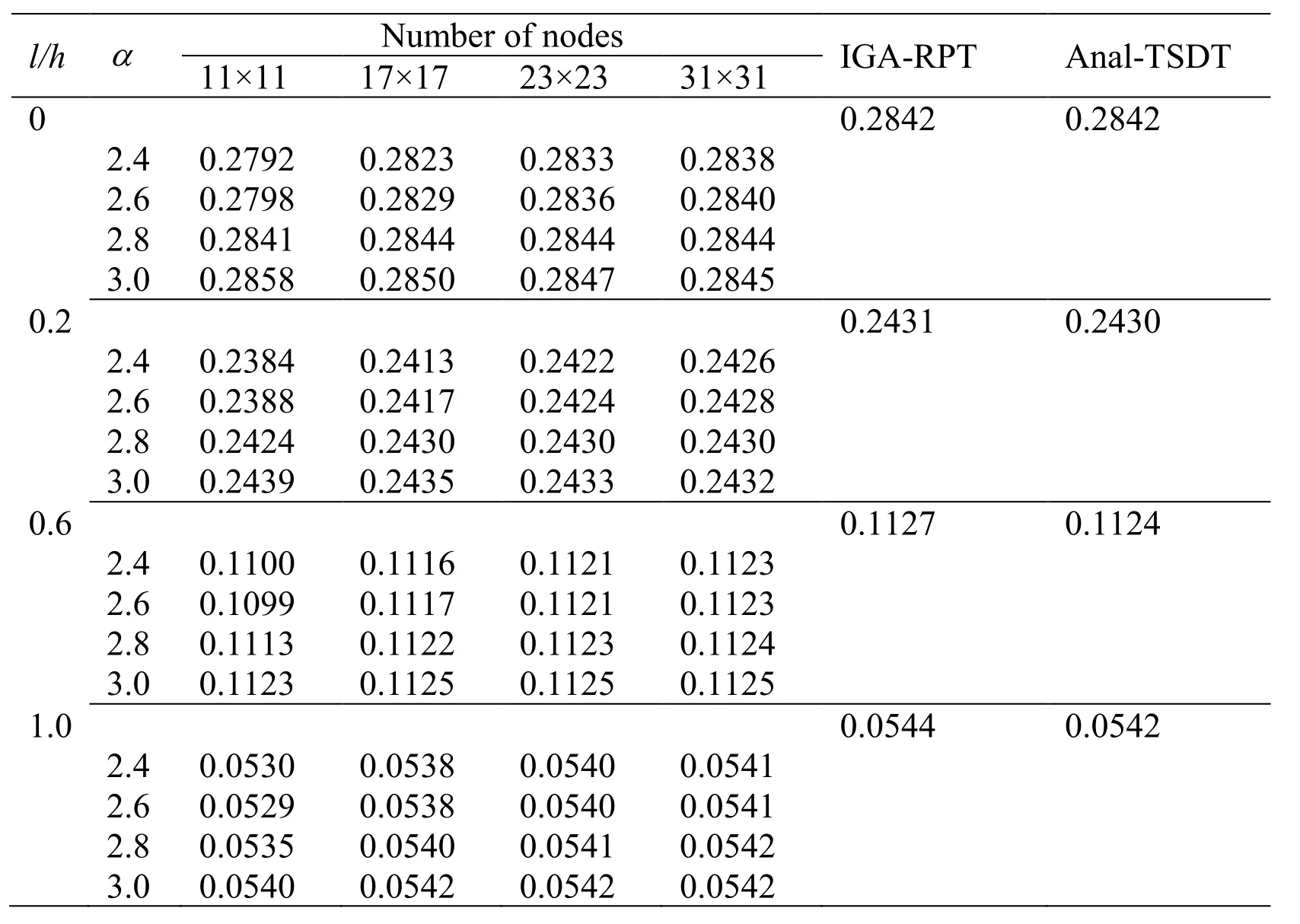
Table 2:Convergence of non-dimensional central displacementof simply supported isotropic square microplate subjected to sinusoidally distributed load

l/h 11×11 17×17 23×23 31×31 Number of nodes IGA-RPT Anal-TSDT 0 0.2842 0.2842 2.4 0.2792 0.2823 0.2833 0.2838 2.6 0.2798 0.2829 0.2836 0.2840 2.8 0.2841 0.2844 0.2844 0.2844 3.0 0.2858 0.2850 0.2847 0.2845 0.2 0.2431 0.2430 2.4 0.2384 0.2413 0.2422 0.2426 2.6 0.2388 0.2417 0.2424 0.2428 2.8 0.2424 0.2430 0.2430 0.2430 3.0 0.2439 0.2435 0.2433 0.2432 0.6 0.1127 0.1124 2.4 0.1100 0.1116 0.1121 0.1123 2.6 0.1099 0.1117 0.1121 0.1123 2.8 0.1113 0.1122 0.1123 0.1124 3.0 0.1123 0.1125 0.1125 0.1125 1.0 0.0544 0.0542 2.4 0.0530 0.0538 0.0540 0.0541 2.6 0.0529 0.0538 0.0540 0.0541 2.8 0.0535 0.0540 0.0541 0.0542 3.0 0.0540 0.0542 0.0542 0.0542

Figure 4:A distributed nodes:(a)Simply supported BCs;(b)Fully clamped BCs

4.1.2 Accuracy of present solution

A FG square microplate made of a mixture of ceramic(Al2O3)and metal(Al)is subjected to a sinusoidally distributed transverse load.Two types of simply supported and fully clamped BCs are used.

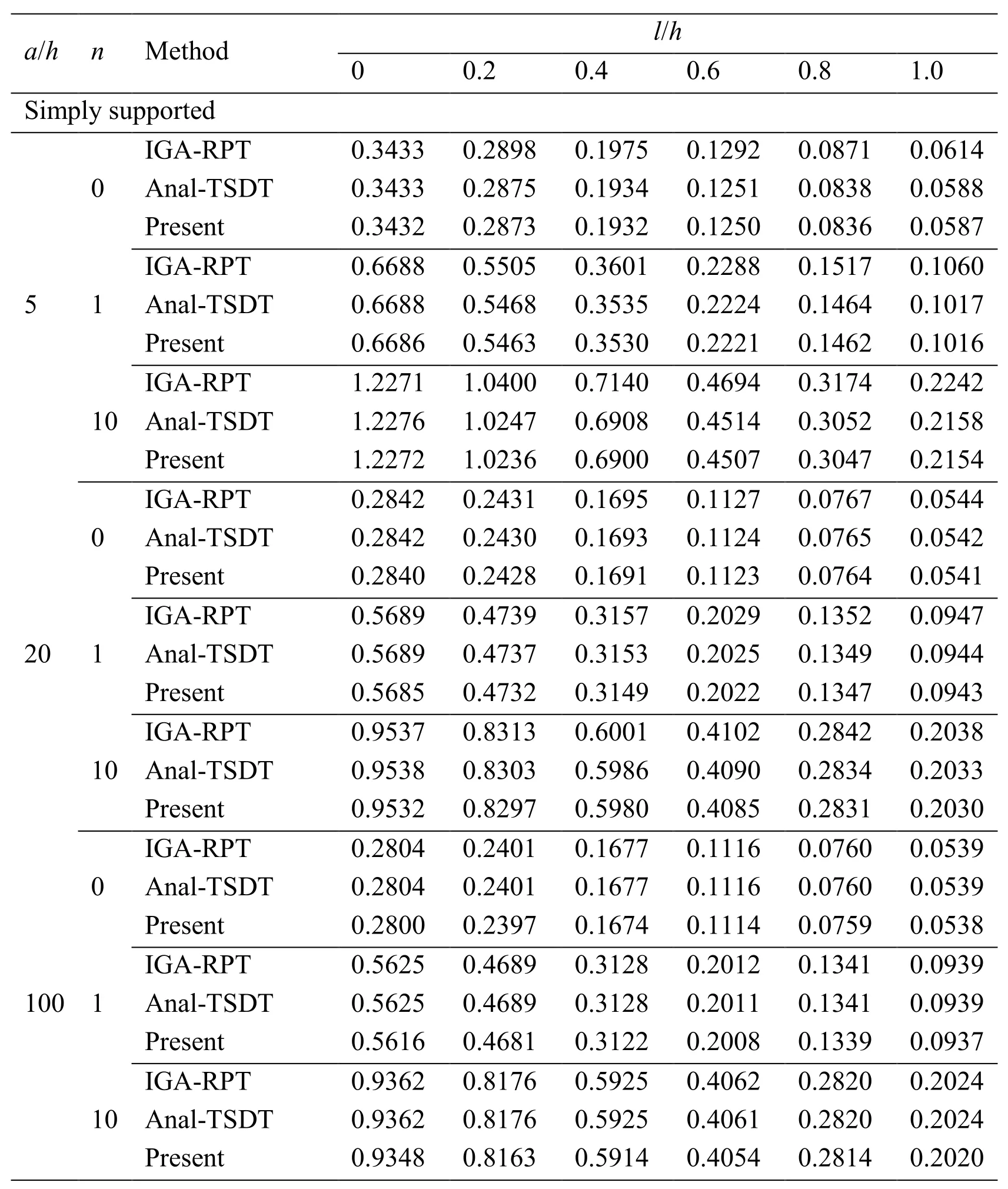
Table 3:Non-dimensional displacement of the Al/Al2O3 square microplate subjected to sinusoidally distributed load

a/h n Method l/h 0 0.2 0.4 0.6 0.8 1.0 Simply supported IGA-RPT 0.3433 0.2898 0.1975 0.1292 0.0871 0.0614 0Anal-TSDT 0.3433 0.2875 0.1934 0.1251 0.0838 0.0588 Present 0.3432 0.2873 0.1932 0.1250 0.0836 0.0587 IGA-RPT 0.6688 0.5505 0.3601 0.2288 0.1517 0.1060 51Anal-TSDT 0.6688 0.5468 0.3535 0.2224 0.1464 0.1017 Present 0.6686 0.5463 0.3530 0.2221 0.1462 0.1016 IGA-RPT 1.2271 1.0400 0.7140 0.4694 0.3174 0.2242 10Anal-TSDT 1.2276 1.0247 0.6908 0.4514 0.3052 0.2158 Present 1.2272 1.0236 0.6900 0.4507 0.3047 0.2154 IGA-RPT 0.2842 0.2431 0.1695 0.1127 0.0767 0.0544 0Anal-TSDT 0.2842 0.2430 0.1693 0.1124 0.0765 0.0542 Present 0.2840 0.2428 0.1691 0.1123 0.0764 0.0541 IGA-RPT 0.5689 0.4739 0.3157 0.2029 0.1352 0.0947 201Anal-TSDT 0.5689 0.4737 0.3153 0.2025 0.1349 0.0944 Present 0.5685 0.4732 0.3149 0.2022 0.1347 0.0943 IGA-RPT 0.9537 0.8313 0.6001 0.4102 0.2842 0.2038 10Anal-TSDT 0.9538 0.8303 0.5986 0.4090 0.2834 0.2033 Present 0.9532 0.8297 0.5980 0.4085 0.2831 0.2030 IGA-RPT 0.2804 0.2401 0.1677 0.1116 0.0760 0.0539 0Anal-TSDT 0.2804 0.2401 0.1677 0.1116 0.0760 0.0539 Present 0.2800 0.2397 0.1674 0.1114 0.0759 0.0538 IGA-RPT 0.5625 0.4689 0.3128 0.2012 0.1341 0.0939 1001Anal-TSDT 0.5625 0.4689 0.3128 0.2011 0.1341 0.0939 Present 0.5616 0.4681 0.3122 0.2008 0.1339 0.0937 IGA-RPT 0.9362 0.8176 0.5925 0.4062 0.2820 0.2024 10Anal-TSDT 0.9362 0.8176 0.5925 0.4061 0.2820 0.2024 Present 0.9348 0.8163 0.5914 0.4054 0.2814 0.2020

Tab.3 shows the non-dimensional central displacement of isotropic FG square microplates for several values of power index(n)and length-to-thickness ratio(a/h)as well as material length scale-to-thickness ratio(l/h).Reference solutions reported by Thai et al.[Thai and Κim(2013)] using the TSDT analytical model(5 degrees of freedom(DOFs)),Nguyen et al.[Nguyen,Nguyen,Wahab et al.(2017)] using the IGA-RPT model(4 DOFs)and the present HSDT model using IGA are also listed.We observe that obtained results almost match with the reference ones.Basically,the non-dimensional displacements derived from the IGA-RPT model are larger than those of the exact-TSDT model due to using two different theory models.The results of the present model are mostly close to the published ones in Thai et al.[Thai and Κim(2013)] than those studied by Nguyen et al.[Nguyen,Nguyen,Wahab et al.(2017)] due to using the same TSDT instead of RPT.Also,

Tab.3 shows that an increase of l/h results in a decline of the non-dimensional displacement.The stiffness of FG microplate increases when considering the sizedependent effect.When the power index n is increased,the non-dimensional displacement is increased due to decreasing the stiffness of FG microplate.Reciprocally,the length-to-thickness ratio a/h risen leads to a reduction of the non-dimensional displacement.For the case of l/h=1,the non-dimensional displacement predicted by the size-dependent model is much smaller than about five times those predicted by the classical plate model.

4.2 Free vibration and buckling analyses

4.2.1 Isotropic FG square microplate

A simply supported isotropic Al/Al2O3FG square microplate as given in Subsection 4.1.2 is used for free vibration analysis,while,for buckling analysis,material properties are taken by Reddy [Reddy(2000)]:Ec=14.4 GPa ,Em=1.44 GPa and vc= vm=0.38.Tab.4 lists the first non-dimensional natural frequency.For comparison,the results reported by Thai et al.[Thai and Κim(2013)] and Nguyen et al.[Nguyen,Nguyen,Wahab et al.(2017)] is also provided in Tab.4.Also,the non-dimensional critical buckling load obtained by the present meshfree solution based on HSDT,the analytical solution based on FSDT [Thai and Choi(2013)],the analytical solution based on RPT [He,Lou,Zhang et al.(2015)] and the IGA solution based on RPT [Nguyen,Nguyen,Wahab et al.(2017)]is given in Tab.5.As observed from Tab.4 and Tab.5,a good agreement with those reference results is achieved.Basically,the results of the present model are slightly larger than compared to those of the above reference solutions for both non-dimensional natural frequency and critical buckling load.Especially,obtained results are mostly close to the published solution by Thai et al.[Thai and Κim(2013)] than that of other published results because of using the same HSDT model.Moreover,according to two above tables,it can be observed thatandincrease as l/h increases.The vibration and buckling responses predicted by the MCST are always larger than those of the classical theory.The non-dimensional natural frequency and critical buckling load given by the classical plate model are much smaller than two and five times those given by the size-dependent model with l/h=1,respectively.These differences decrease when the plate thickness of becomes large.We can conclude that the stiffness of FG microplate increases with respect to inclusion of the size effect leading to a rise of natural frequency as well as critical buckling load.

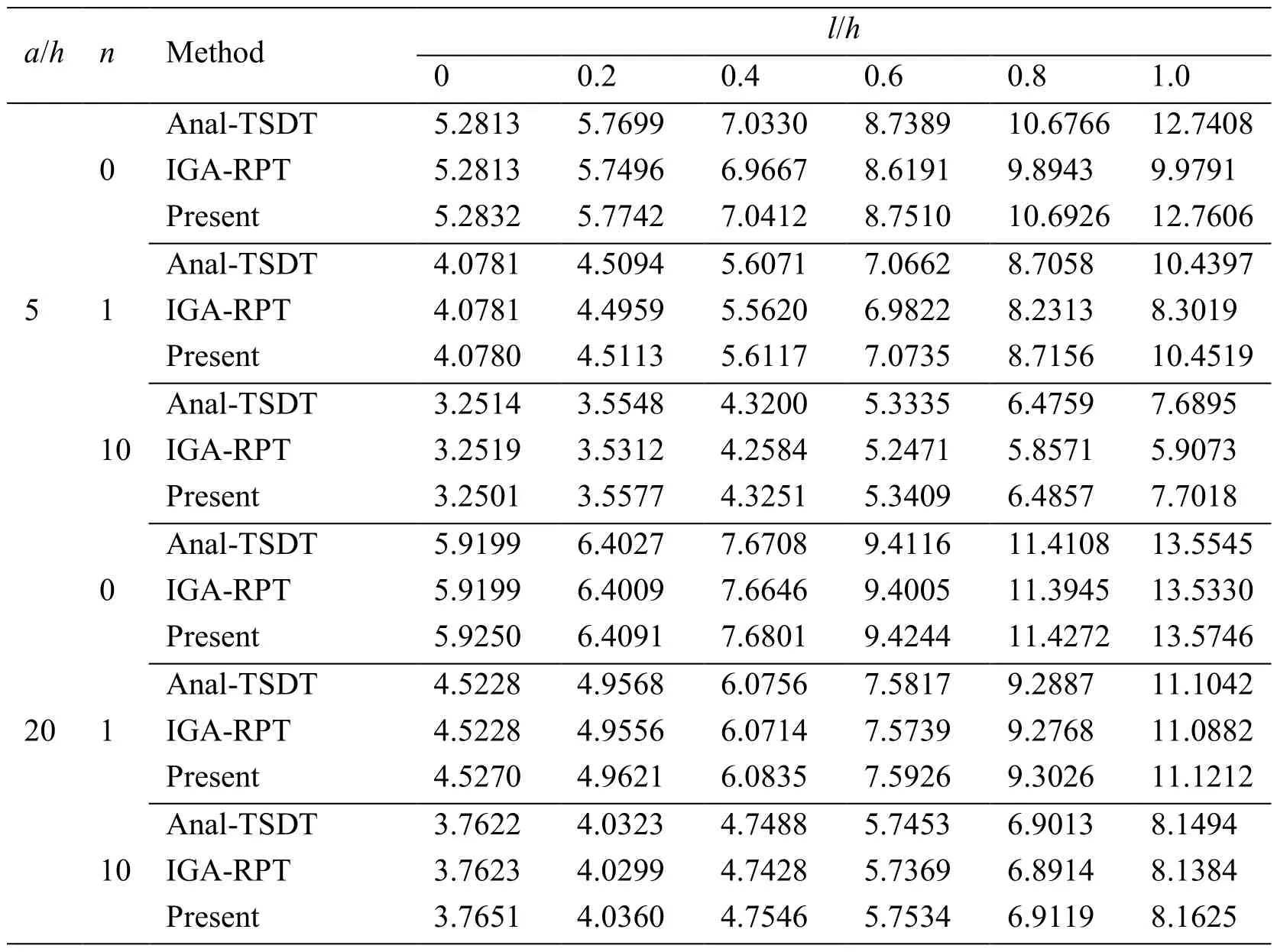
Table 4:The first non-dimensional natural frequency of simply supported FG square microplate

a/h n Method l/h 0 0.2 0.4 0.6 0.8 1.0 Anal-TSDT 5.2813 5.7699 7.0330 8.7389 10.6766 12.7408 0IGA-RPT 5.2813 5.7496 6.9667 8.6191 9.8943 9.9791 Present 5.2832 5.7742 7.0412 8.7510 10.6926 12.7606 Anal-TSDT 4.0781 4.5094 5.6071 7.0662 8.7058 10.4397 51IGA-RPT 4.0781 4.4959 5.5620 6.9822 8.2313 8.3019 Present 4.0780 4.5113 5.6117 7.0735 8.7156 10.4519 Anal-TSDT 3.2514 3.5548 4.3200 5.3335 6.4759 7.6895 10IGA-RPT 3.2519 3.5312 4.2584 5.2471 5.8571 5.9073 Present 3.2501 3.5577 4.3251 5.3409 6.4857 7.7018 Anal-TSDT 5.9199 6.4027 7.6708 9.4116 11.4108 13.5545 0IGA-RPT 5.9199 6.4009 7.6646 9.4005 11.3945 13.5330 Present 5.9250 6.4091 7.6801 9.4244 11.4272 13.5746 Anal-TSDT 4.5228 4.9568 6.0756 7.5817 9.2887 11.1042 201IGA-RPT 4.5228 4.9556 6.0714 7.5739 9.2768 11.0882 Present 4.5270 4.9621 6.0835 7.5926 9.3026 11.1212 Anal-TSDT 3.7622 4.0323 4.7488 5.7453 6.9013 8.1494 10IGA-RPT 3.7623 4.0299 4.7428 5.7369 6.8914 8.1384 Present 3.7651 4.0360 4.7546 5.7534 6.9119 8.1625

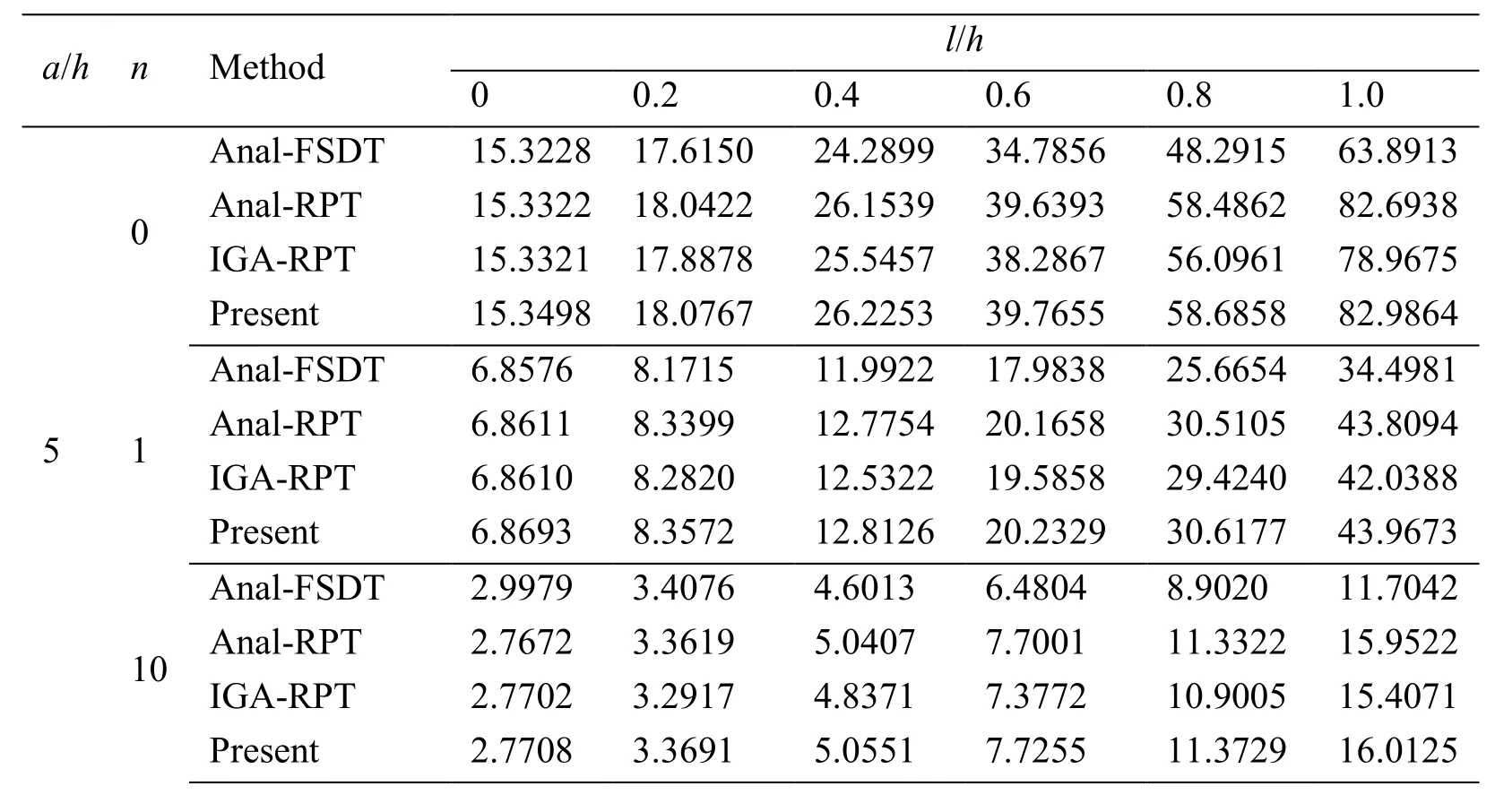
Table 5:Comparison of non-dimensional critical buckling load of simply supported FG square microplates

a/h n Method l/h 0 0.2 0.4 0.6 0.8 1.0 Anal-FSDT 15.3228 17.6150 24.2899 34.7856 48.2915 63.8913 0Anal-RPT 15.3322 18.0422 26.1539 39.6393 58.4862 82.6938 IGA-RPT 15.3321 17.8878 25.5457 38.2867 56.0961 78.9675 Present 15.3498 18.0767 26.2253 39.7655 58.6858 82.9864 Anal-FSDT 6.8576 8.1715 11.9922 17.9838 25.6654 34.4981 51Anal-RPT 6.8611 8.3399 12.7754 20.1658 30.5105 43.8094 IGA-RPT 6.8610 8.2820 12.5322 19.5858 29.4240 42.0388 Present 6.8693 8.3572 12.8126 20.2329 30.6177 43.9673 Anal-FSDT 2.9979 3.4076 4.6013 6.4804 8.9020 11.7042 10Anal-RPT 2.7672 3.3619 5.0407 7.7001 11.3322 15.9522 IGA-RPT 2.7702 3.2917 4.8371 7.3772 10.9005 15.4071 Present 2.7708 3.3691 5.0551 7.7255 11.3729 16.0125

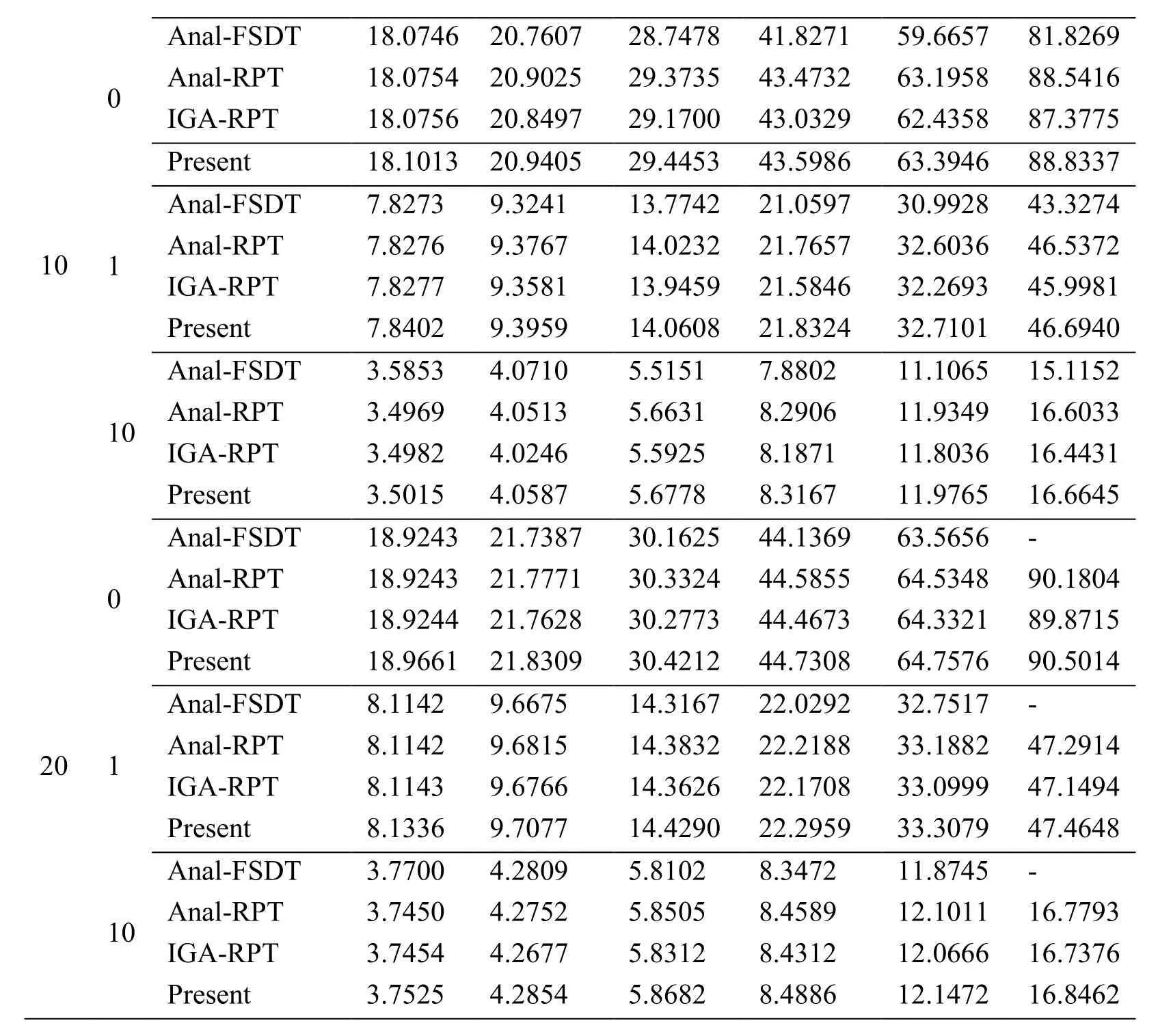
Anal-FSDT 18.0746 20.7607 28.7478 41.8271 59.6657 81.8269 0Anal-RPT 18.0754 20.9025 29.3735 43.4732 63.1958 88.5416 IGA-RPT 18.0756 20.8497 29.1700 43.0329 62.4358 87.3775 Present 18.1013 20.9405 29.4453 43.5986 63.3946 88.8337 Anal-FSDT 7.8273 9.3241 13.7742 21.0597 30.9928 43.3274 101Anal-RPT 7.8276 9.3767 14.0232 21.7657 32.6036 46.5372 IGA-RPT 7.8277 9.3581 13.9459 21.5846 32.2693 45.9981 Present 7.8402 9.3959 14.0608 21.8324 32.7101 46.6940 Anal-FSDT 3.5853 4.0710 5.5151 7.8802 11.1065 15.1152 10Anal-RPT 3.4969 4.0513 5.6631 8.2906 11.9349 16.6033 IGA-RPT 3.4982 4.0246 5.5925 8.1871 11.8036 16.4431 Present 3.5015 4.0587 5.6778 8.3167 11.9765 16.6645 Anal-FSDT 18.9243 21.7387 30.1625 44.1369 63.5656 -0Anal-RPT 18.9243 21.7771 30.3324 44.5855 64.5348 90.1804 IGA-RPT 18.9244 21.7628 30.2773 44.4673 64.3321 89.8715 Present 18.9661 21.8309 30.4212 44.7308 64.7576 90.5014 Anal-FSDT 8.1142 9.6675 14.3167 22.0292 32.7517 -201Anal-RPT 8.1142 9.6815 14.3832 22.2188 33.1882 47.2914 IGA-RPT 8.1143 9.6766 14.3626 22.1708 33.0999 47.1494 Present 8.1336 9.7077 14.4290 22.2959 33.3079 47.4648 Anal-FSDT 3.7700 4.2809 5.8102 8.3472 11.8745 -10Anal-RPT 3.7450 4.2752 5.8505 8.4589 12.1011 16.7793 IGA-RPT 3.7454 4.2677 5.8312 8.4312 12.0666 16.7376 Present 3.7525 4.2854 5.8682 8.4886 12.1472 16.8462

4.2.2 Isotropic FG circular plate

We consider an isotropic Ti/ZrO2FG circular microplate with the radius R and the thickness h subjected to a uniform radial compression,as shown in Fig.5(a).The simply supported and fully clamped boundary conditions are studied and a distribution of nodes is shown in Fig.5(b-c).In addition,the effective Young’s modulus and Poison’s ratio are computed by:

Again,different values of power index,thickness-to-radius ratio and material length scale-to-thickness ratio are studied.The non-dimensional critical buckling load of the present model is listed in Tab.6.Obtained results of l/h=0 are compared with those reported by Ma et al.[Ma and Wang(2004)] using the analytical solution based on FSDT and TSDT,Saidi et al.[Saidi,Rasouli and Sahraee(2009)] using the analytical solution based on unconstrained third-order shear deformation plate theory(UTSDT)and Nguyen-Xuan et al.[Nguyen-Xuan,Tran,Thai et al.(2014)] using the IGA based on RPT.The present results match well with the referenced ones for the case of l/h=0.In addition,it is noted that the non-dimensional critical buckling load increases when increasing the material length scale-to-thickness ratio.The stiffness of microplate increases within considering size-dependent effects.The difference of critical buckling load between the present size-dependent model(l/h=1)and the classical model is most significant but this difference decreases when the thickness of the microplate becomes large.The first six modes shape of buckling response of fully clamped isotropic FG circular microplate is plotted in Fig.6.

Figure 5:The circular microplate:a)Geometry; b)Distribution nodes for simply supported BC; Distribution nodes for simply clamped BC

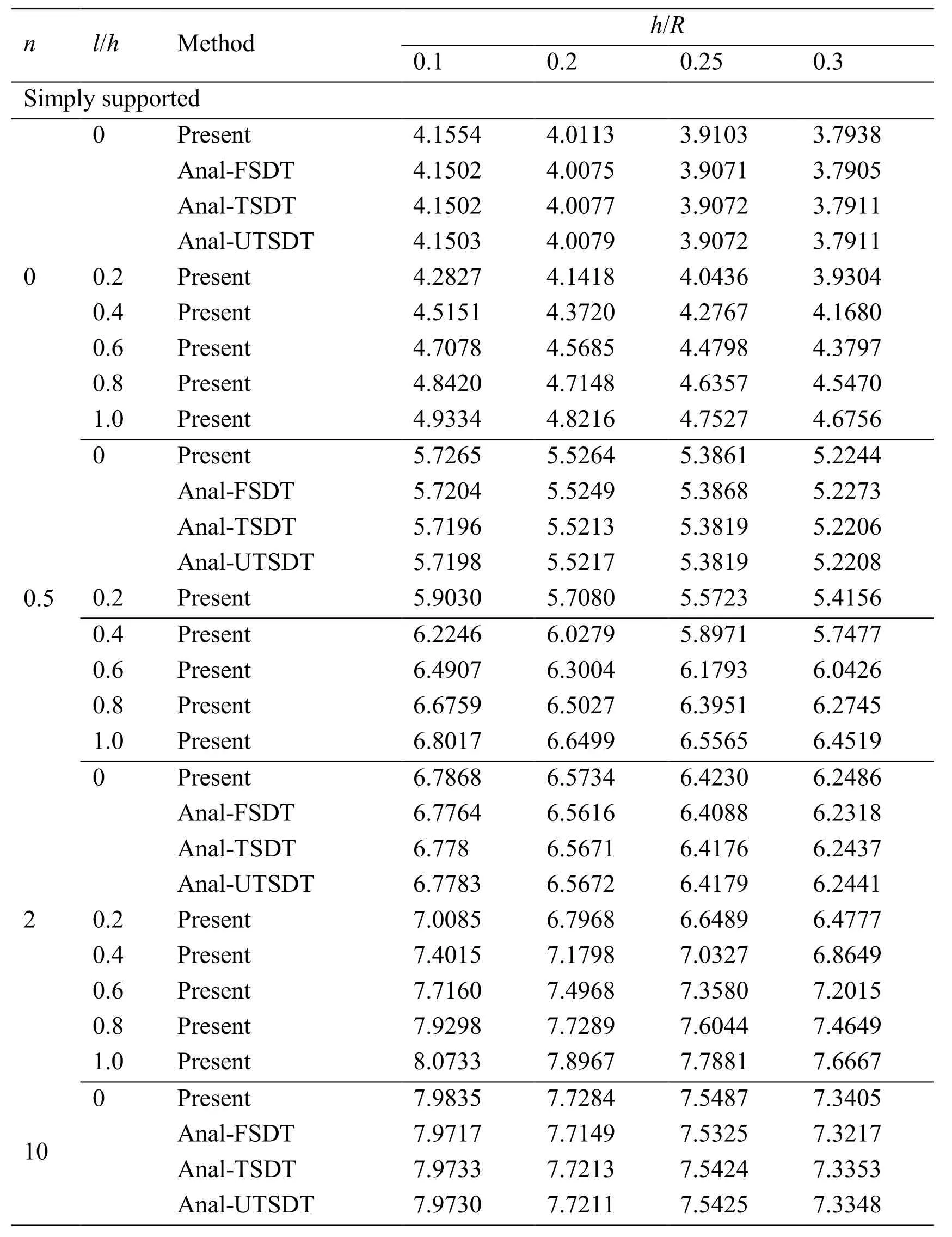
Table 6:Non-dimensional critical buckling load factorof isotropic FG circular microplates

n l/h Method h/R 0.1 0.2 0.25 0.3 Simply supported 0 Present 4.1554 4.0113 3.9103 3.7938 Anal-FSDT 4.1502 4.0075 3.9071 3.7905 Anal-TSDT 4.1502 4.0077 3.9072 3.7911 Anal-UTSDT 4.1503 4.0079 3.9072 3.7911 00.2 Present 4.2827 4.1418 4.0436 3.9304 0.4 Present 4.5151 4.3720 4.2767 4.1680 0.6 Present 4.7078 4.5685 4.4798 4.3797 0.8 Present 4.8420 4.7148 4.6357 4.5470 1.0 Present 4.9334 4.8216 4.7527 4.6756 0 Present 5.7265 5.5264 5.3861 5.2244 Anal-FSDT 5.7204 5.5249 5.3868 5.2273 Anal-TSDT 5.7196 5.5213 5.3819 5.2206 Anal-UTSDT 5.7198 5.5217 5.3819 5.2208 0.50.2 Present 5.9030 5.7080 5.5723 5.4156 0.4 Present 6.2246 6.0279 5.8971 5.7477 0.6 Present 6.4907 6.3004 6.1793 6.0426 0.8 Present 6.6759 6.5027 6.3951 6.2745 1.0 Present 6.8017 6.6499 6.5565 6.4519 0 Present 6.7868 6.5734 6.4230 6.2486 Anal-FSDT 6.7764 6.5616 6.4088 6.2318 Anal-TSDT 6.778 6.5671 6.4176 6.2437 Anal-UTSDT 6.7783 6.5672 6.4179 6.2441 20.2 Present 7.0085 6.7968 6.6489 6.4777 0.4 Present 7.4015 7.1798 7.0327 6.8649 0.6 Present 7.7160 7.4968 7.3580 7.2015 0.8 Present 7.9298 7.7289 7.6044 7.4649 1.0 Present 8.0733 7.8967 7.7881 7.6667 0 Present 7.9835 7.7284 7.5487 7.3405 10Anal-FSDT 7.9717 7.7149 7.5325 7.3217 Anal-TSDT 7.9733 7.7213 7.5424 7.3353 Anal-UTSDT 7.9730 7.7211 7.5425 7.3348

0.2 Present 8.2409 7.9877 7.8109 7.6064 0.4 Present 8.6997 8.4345 8.2585 8.0578 0.6 Present 9.0691 8.8065 8.6400 8.4525 0.8 Present 9.3215 9.0800 8.9304 8.7629 1.0 Present 9.4914 9.2786 9.0017 9.1479 Fully clamped 0 Present 14.2065 12.5651 11.5961 10.6109 Anal-TSDT 14.089 12.574 11.638 10.670 Anal-UTSDT 14.089 12.575 11.639 10.670 IGA-RPT 14.2023 12.7281 11.8143 10.8666 00.2 Present 16.7292 15.0790 14.0771 13.0388 0.4 Present 24.2239 22.3498 21.1718 19.9246 0.6 Present 36.6708 34.3840 32.9086 31.3169 0.8 Present 54.0748 51.1961 49.3047 47.2345 1.0 Present 76.4396 72.7922 70.3660 67.6829 0 Present 19.5774 17.3032 15.9615 14.5985 Anal-TSDT 19.411 17.311 16.013 14.672 Anal-UTSDT 19.413 17.310 16.012 14.672 IGA-RPT 19.5663 17.5180 16.2506 14.9381 0.50.2 Present 23.0780 20.7999 19.4168 17.9839 0.4 Present 33.4762 30.9155 29.3037 27.5957 0.6 Present 50.7425 47.6515 45.6524 43.4915 0.8 Present 78.8827 71.0254 68.4831 65.6935 1.0 Present 105.9024 101.0456 97.8042 94.2092 0 Present 23.2864 20.8136 19.3306 17.8035 Anal-TSDT 23.074 20.803 19.377 17.882 Anal-UTSDT 23.075 20.805 19.378 17.881 IGA-RPT 23.2592 21.0569 19.6687 18.2099 20.2 Present 25.2108 25.2108 23.6579 22.0308 0.4 Present 40.9735 37.9928 36.1025 34.0859 0.6 Present 62.9775 59.1824 56.7222 54.0572 0.8 Present 93.7558 88.8070 85.5498 81.9791 1.0 Present 133.3138 126.8754 122.5941 117.8601 0 Present 27.3717 24.4195 22.6543 20.8406 10Anal-TSDT 27.133 24.423 22.725 20.948 Anal-UTSDT 27.131 24.422 22.725 20.949

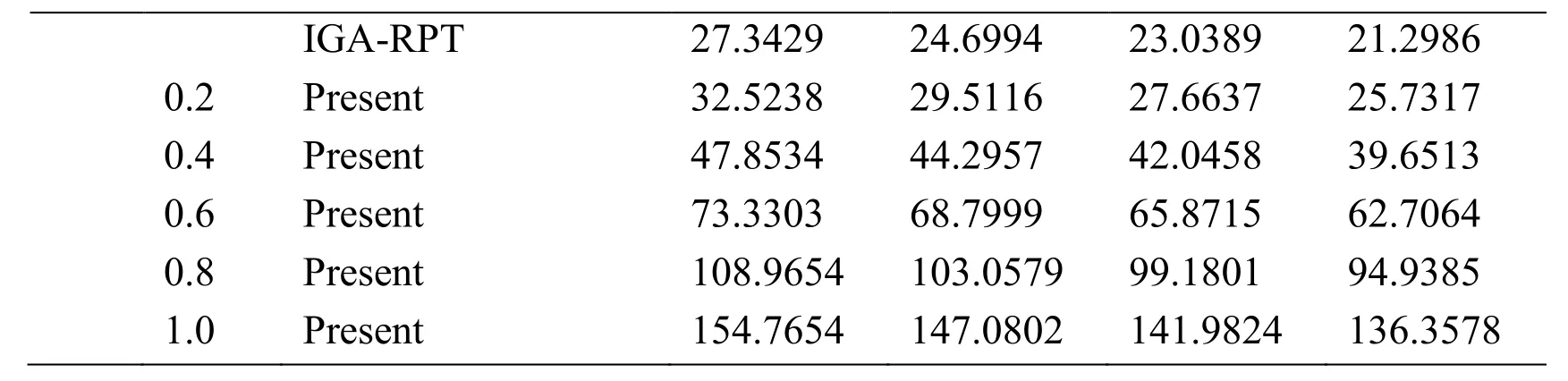
IGA-RPT 27.3429 24.6994 23.0389 21.2986 0.2 Present 32.5238 29.5116 27.6637 25.7317 0.4 Present 47.8534 44.2957 42.0458 39.6513 0.6 Present 73.3303 68.7999 65.8715 62.7064 0.8 Present 108.9654 103.0579 99.1801 94.9385 1.0 Present 154.7654 147.0802 141.9824 136.3578

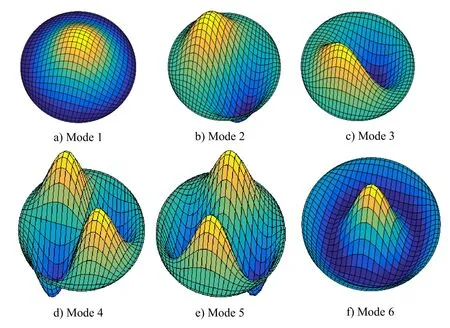
Figure 6:The first six mode shapes of buckling response of fully clamped isotropic FG circular microplate with n=10,h/R=0.1 and l/h=1

4.2.3 Isotropic FG square plate with a complicated cutout

We consider a simply supported square microplate with a complicated cutout,as shown in Fig.7(a).A set of nodes(541 nodes)of the isotropic FG microplate is illustrated by Fig.7(b).This microplate is made of zirconia(ZrO2-2)and aluminum(Al).The nondimensional natural frequency is given bywhere Ecand ρcare the Young’s modulus and density mass of ceramic,respectively.The first six nondimensional natural frequencies of the square FG microplate with a complicated cutout are given in Tab.7.For the case of l/h=0,obtained results are compared with those reported in Nguyen et al.[Nguyen and Nguyen-Xuan(2015)] based on the IGA solution using 3D elasticity theory(IGA-3D)and in [Thai,Ferreira,Wahab et al.(2018)] based on the meshfree solution using HSDT(MF-HSDT).In addition,the present results are available for the case of l/ h ≠0.As given in Tab.7,non-dimensional frequencies increase with increasing of l/h and decrease when increasing the power index value.

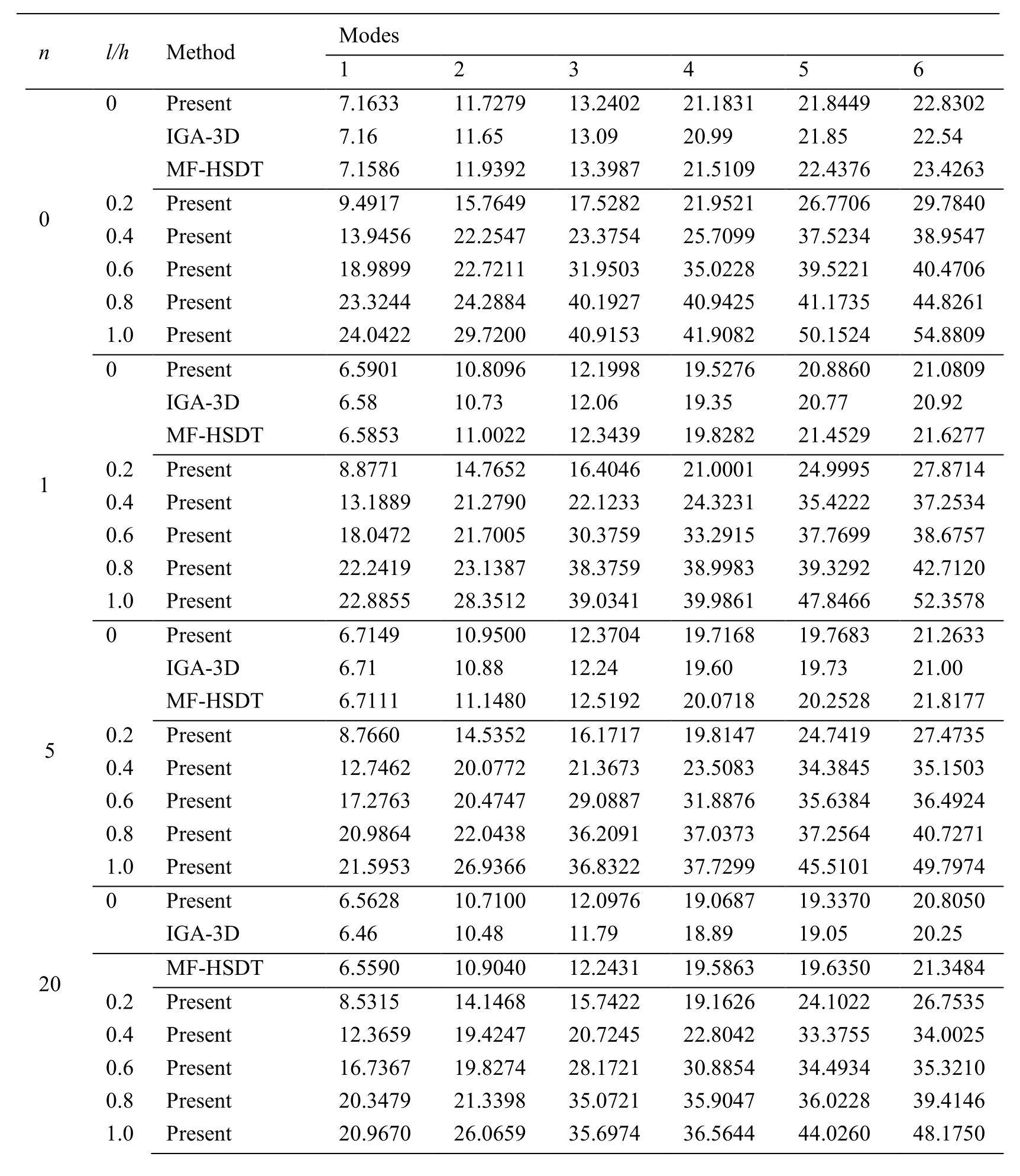
Table 7:Comparisons of non-dimensional frequencies of the isotropic FG square plate of a hole of complicated shape

n l/h Method Modes 1 2 3 4 5 6 0 Present 7.1633 11.7279 13.2402 21.1831 21.8449 22.8302 IGA-3D 7.16 11.65 13.09 20.99 21.85 22.54 MF-HSDT 7.1586 11.9392 13.3987 21.5109 22.4376 23.4263 00.2 Present 9.4917 15.7649 17.5282 21.9521 26.7706 29.7840 0.4 Present 13.9456 22.2547 23.3754 25.7099 37.5234 38.9547 0.6 Present 18.9899 22.7211 31.9503 35.0228 39.5221 40.4706 0.8 Present 23.3244 24.2884 40.1927 40.9425 41.1735 44.8261 1.0 Present 24.0422 29.7200 40.9153 41.9082 50.1524 54.8809 0 Present 6.5901 10.8096 12.1998 19.5276 20.8860 21.0809 IGA-3D 6.58 10.73 12.06 19.35 20.77 20.92 MF-HSDT 6.5853 11.0022 12.3439 19.8282 21.4529 21.6277 10.2 Present 8.8771 14.7652 16.4046 21.0001 24.9995 27.8714 0.4 Present 13.1889 21.2790 22.1233 24.3231 35.4222 37.2534 0.6 Present 18.0472 21.7005 30.3759 33.2915 37.7699 38.6757 0.8 Present 22.2419 23.1387 38.3759 38.9983 39.3292 42.7120 1.0 Present 22.8855 28.3512 39.0341 39.9861 47.8466 52.3578 0 Present 6.7149 10.9500 12.3704 19.7168 19.7683 21.2633 IGA-3D 6.71 10.88 12.24 19.60 19.73 21.00 MF-HSDT 6.7111 11.1480 12.5192 20.0718 20.2528 21.8177 50.2 Present 8.7660 14.5352 16.1717 19.8147 24.7419 27.4735 0.4 Present 12.7462 20.0772 21.3673 23.5083 34.3845 35.1503 0.6 Present 17.2763 20.4747 29.0887 31.8876 35.6384 36.4924 0.8 Present 20.9864 22.0438 36.2091 37.0373 37.2564 40.7271 1.0 Present 21.5953 26.9366 36.8322 37.7299 45.5101 49.7974 0 Present 6.5628 10.7100 12.0976 19.0687 19.3370 20.8050 IGA-3D 6.46 10.48 11.79 18.89 19.05 20.25 20MF-HSDT 6.5590 10.9040 12.2431 19.5863 19.6350 21.3484 0.2 Present 8.5315 14.1468 15.7422 19.1626 24.1022 26.7535 0.4 Present 12.3659 19.4247 20.7245 22.8042 33.3755 34.0025 0.6 Present 16.7367 19.8274 28.1721 30.8854 34.4934 35.3210 0.8 Present 20.3479 21.3398 35.0721 35.9047 36.0228 39.4146 1.0 Present 20.9670 26.0659 35.6974 36.5644 44.0260 48.1750

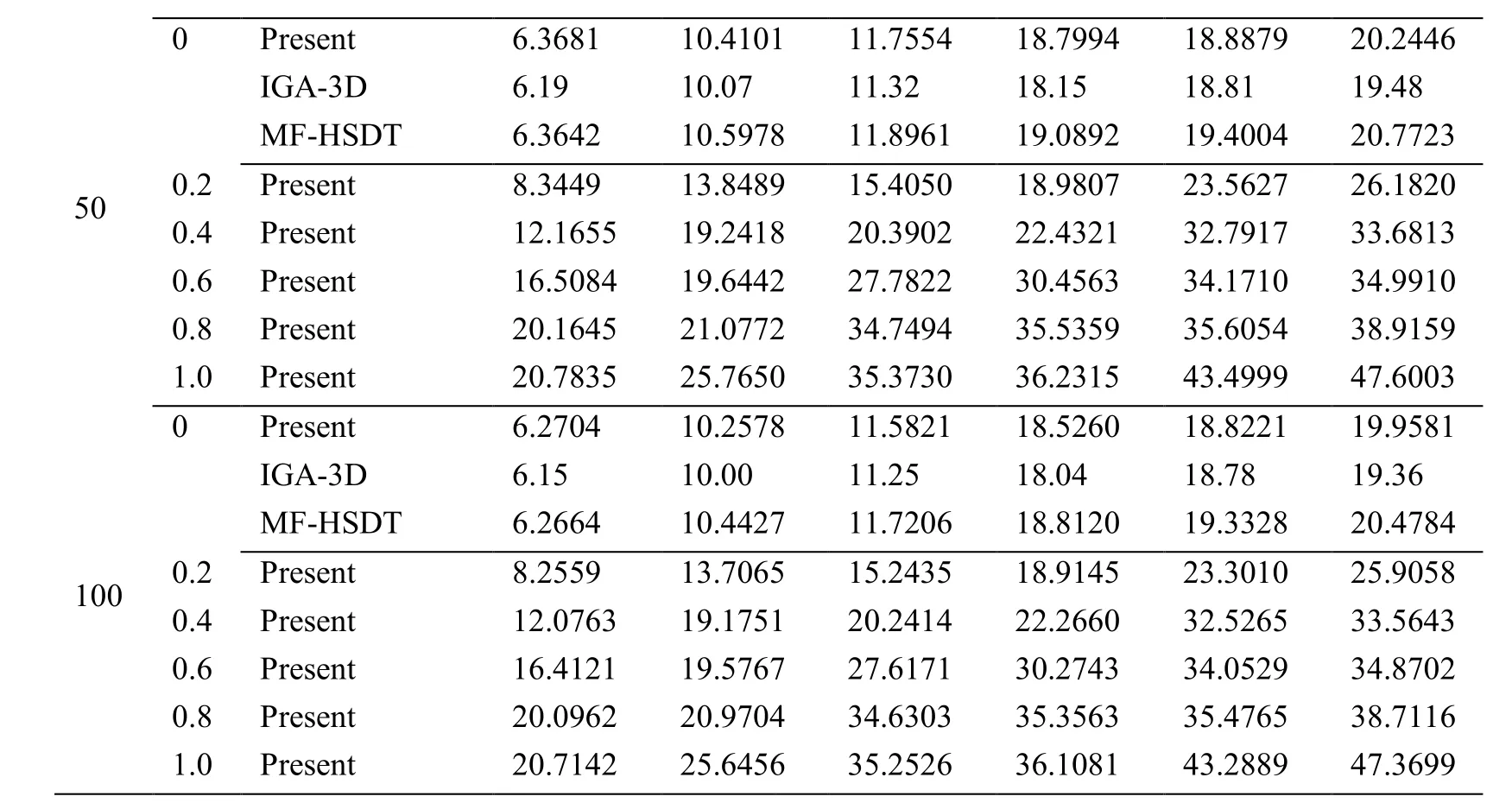
0 Present 6.3681 10.4101 11.7554 18.7994 18.8879 20.2446 IGA-3D 6.19 10.07 11.32 18.15 18.81 19.48 MF-HSDT 6.3642 10.5978 11.8961 19.0892 19.4004 20.7723 500.2 Present 8.3449 13.8489 15.4050 18.9807 23.5627 26.1820 0.4 Present 12.1655 19.2418 20.3902 22.4321 32.7917 33.6813 0.6 Present 16.5084 19.6442 27.7822 30.4563 34.1710 34.9910 0.8 Present 20.1645 21.0772 34.7494 35.5359 35.6054 38.9159 1.0 Present 20.7835 25.7650 35.3730 36.2315 43.4999 47.6003 0 Present 6.2704 10.2578 11.5821 18.5260 18.8221 19.9581 IGA-3D 6.15 10.00 11.25 18.04 18.78 19.36 MF-HSDT 6.2664 10.4427 11.7206 18.8120 19.3328 20.4784 1000.2 Present 8.2559 13.7065 15.2435 18.9145 23.3010 25.9058 0.4 Present 12.0763 19.1751 20.2414 22.2660 32.5265 33.5643 0.6 Present 16.4121 19.5767 27.6171 30.2743 34.0529 34.8702 0.8 Present 20.0962 20.9704 34.6303 35.3563 35.4765 38.7116 1.0 Present 20.7142 25.6456 35.2526 36.1081 43.2889 47.3699

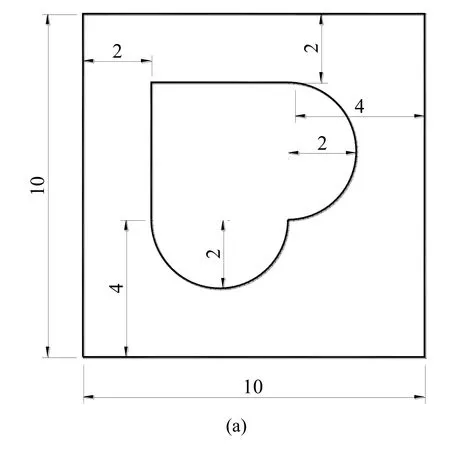
Figure 7:Geometry and a set of distributed node of a square plate with a complicated hole

4.2.4 FGM sandwich square plate

This final example is a simply supported sandwich FG square microplate making from Al/Al2O3.To evaluate the natural frequency and critical buckling load of sandwich FG square microplate,six types of the bottom-core-top thickness ratio consisting of hb-hc-ht=1-0-1,2-1-2,2-1-1,1-1-1,2-2-1,1-2-1 and various values of the power index as well as material length scale-to-thickness ratio are studied.As known,the solutions using MCST for free vibration and buckling analyses of sandwich FG square microplates are not available in the literature.Therefore,present results are only compared with other referenced ones without considering the size effects.For comparison with l/h=0,the non-dimensional natural frequency given by Li et al.[Li,Lu and Κou(2008)] using the analytical solution(Anal)based on 3D elasticity theory,Zenkour [Zenkour(2005)] using the analytical solution based on TSDT and SSDT and Thai et al.[Thai,Κulasegaram,Tran et al.(2014)] using IGA based on TSDT are also provided in Tab.8,while the bi-axial critical buckling load reported by Reddy [Reddy(2000)] based on the Anal-TSDT solution,Zenkour [Zenkour(2005)] based on the Anal-SSDT solution,Neves et al.[Neves,Ferreira,Carrera et al.(2013)] based on the meshfree-HSDT solution(MF-HSDT)and Thai et al.[Thai,Κulasegaram,Tran et al.(2014] based on IGA-TSDT are given in Tab.9.According to Tab.8 and Tab.9,it is again seen that a rise of the non-dimensional natural frequency and bi-axial critical buckling load is found when increasing the material length scale-to-thickness ratio.Also,the stiffness of sandwich FG microplate increases within considering size effects.In particular,most of non-dimensional natural frequency and critical buckling load with respect to six types of the bottom-core-top thickness ratio predicted by the present sizedependent MΚI-HSDT model are much larger than two and five times those predicted by the classical MΚI-HSDT model,respectively.In addition,a change of the bottom-coretop thickness ratio from 1 -0-1to 1- 2 -1also brings to an increase of the nondimensional natural frequency as well as critical buckling load.Moreover,Tab.10 shows the first five non-dimensional natural frequencies and mode shapes of sandwich FG square microplate corresponding with hb-hc-ht=2-1-2.Besides,the first six mode shapes of sandwich FG square microplate are plotted in Fig.8.

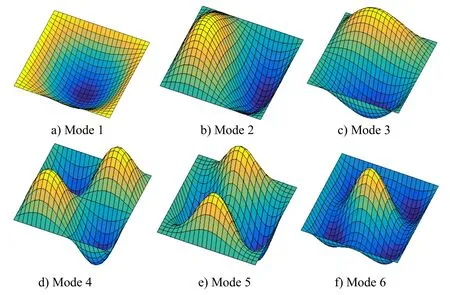
Figure 8:The first six modes shape of dynamic response of simply supported sandwich FG square microplate with n=1,l/h=1 and h b-h c-h t=2??

Table 8:The natural frequencyof the simply supported sandwich FG microplate with a/h=10

n l/h Method 1-0-1 2-1-2 2-1-1 1-1-1 2-2-1 1-2-1 0 Present 1.4451 1.4849 1.5073 1.5201 1.5480 1.5754 Anal-3D 1.4461 1.4861 1.5084 1.5213 1.5493 1.5766 Anal-TSDT 1.4442 1.4841 1.5125 1.5192 1.5520 1.5745 Anal-SSDT 1.4443 1.4842 1.5126 1.5193 1.5520 1.5745 0.5IGA-TSDT 1.4443 1.4841 1.5064 1.5192 1.5472 1.5745 0.2 Present 1.5984 1.6420 1.6640 1.6785 1.7062 1.7343 0.4 Present 1.9883 2.0415 2.0638 2.0825 2.1105 2.1414 0.6 Present 2.5065 2.5728 2.5965 2.6206 2.6505 2.6858 0.8 Present 3.0888 3.1700 3.1962 3.2263 3.2594 3.3004 1.0 Present 3.7052 3.8022 3.8316 3.8679 3.9050 3.9524

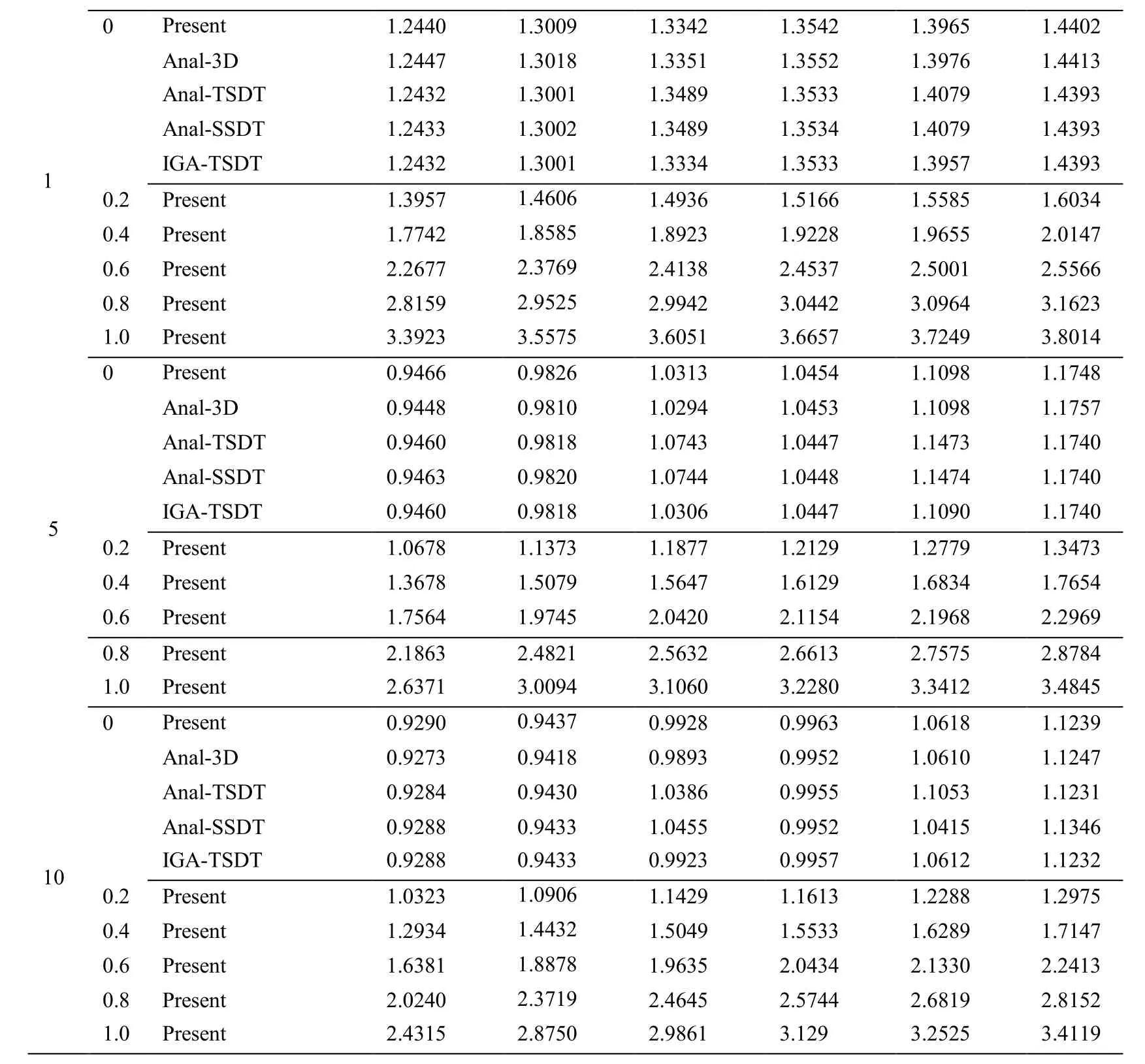
0 Present 1.2440 1.3009 1.3342 1.3542 1.3965 1.4402 Anal-3D 1.2447 1.3018 1.3351 1.3552 1.3976 1.4413 Anal-TSDT 1.2432 1.3001 1.3489 1.3533 1.4079 1.4393 Anal-SSDT 1.2433 1.3002 1.3489 1.3534 1.4079 1.4393 1 IGA-TSDT 1.2432 1.3001 1.3334 1.3533 1.3957 1.4393 0.2 Present 1.3957 1.4606 1.4936 1.5166 1.5585 1.6034 0.4 Present 1.7742 1.8585 1.8923 1.9228 1.9655 2.0147 0.6 Present 2.2677 2.3769 2.4138 2.4537 2.5001 2.5566 0.8 Present 2.8159 2.9525 2.9942 3.0442 3.0964 3.1623 1.0 Present 3.3923 3.5575 3.6051 3.6657 3.7249 3.8014 0 Present 0.9466 0.9826 1.0313 1.0454 1.1098 1.1748 Anal-3D 0.9448 0.9810 1.0294 1.0453 1.1098 1.1757 Anal-TSDT 0.9460 0.9818 1.0743 1.0447 1.1473 1.1740 Anal-SSDT 0.9463 0.9820 1.0744 1.0448 1.1474 1.1740 5 IGA-TSDT 0.9460 0.9818 1.0306 1.0447 1.1090 1.1740 0.2 Present 1.0678 1.1373 1.1877 1.2129 1.2779 1.3473 0.4 Present 1.3678 1.5079 1.5647 1.6129 1.6834 1.7654 0.6 Present 1.7564 1.9745 2.0420 2.1154 2.1968 2.2969 0.8 Present 2.1863 2.4821 2.5632 2.6613 2.7575 2.8784 1.0 Present 2.6371 3.0094 3.1060 3.2280 3.3412 3.4845 0 Present 0.9290 0.9437 0.9928 0.9963 1.0618 1.1239 Anal-3D 0.9273 0.9418 0.9893 0.9952 1.0610 1.1247 Anal-TSDT 0.9284 0.9430 1.0386 0.9955 1.1053 1.1231 Anal-SSDT 0.9288 0.9433 1.0455 0.9952 1.0415 1.1346 10IGA-TSDT 0.9288 0.9433 0.9923 0.9957 1.0612 1.1232 0.2 Present 1.0323 1.0906 1.1429 1.1613 1.2288 1.2975 0.4 Present 1.2934 1.4432 1.5049 1.5533 1.6289 1.7147 0.6 Present 1.6381 1.8878 1.9635 2.0434 2.1330 2.2413 0.8 Present 2.0240 2.3719 2.4645 2.5744 2.6819 2.8152 1.0 Present 2.4315 2.8750 2.9861 3.129 3.2525 3.4119

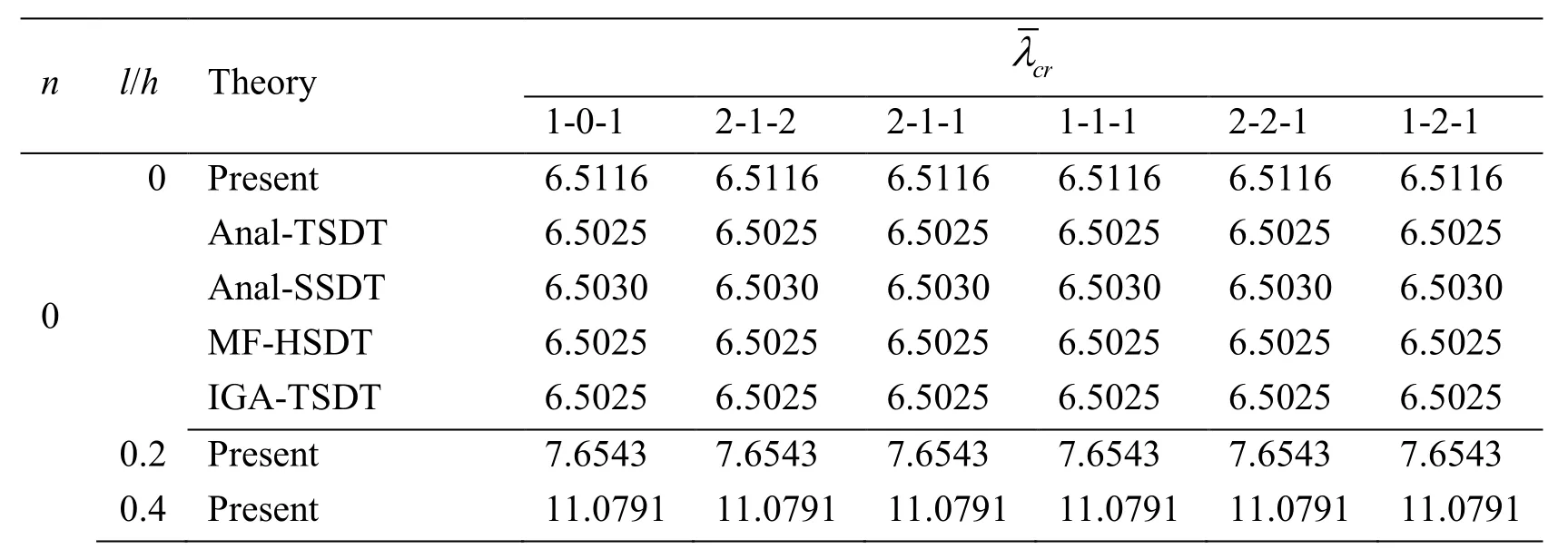
Table 9:The bi-axial non-dimensional critical buckling load of the simply supported sandwich FG square microplate with a/h=10

n l/h Theory 1-0-1 2-1-2 2-1-1 1-1-1 2-2-1 1-2-1 0 Present 6.5116 6.5116 6.5116 6.5116 6.5116 6.5116 Anal-TSDT 6.5025 6.5025 6.5025 6.5025 6.5025 6.5025 0Anal-SSDT 6.5030 6.5030 6.5030 6.5030 6.5030 6.5030 MF-HSDT 6.5025 6.5025 6.5025 6.5025 6.5025 6.5025 IGA-TSDT 6.5025 6.5025 6.5025 6.5025 6.5025 6.5025 0.2 Present 7.6543 7.6543 7.6543 7.6543 7.6543 7.6543 0.4 Present 11.0791 11.0791 11.0791 11.0791 11.0791 11.0791

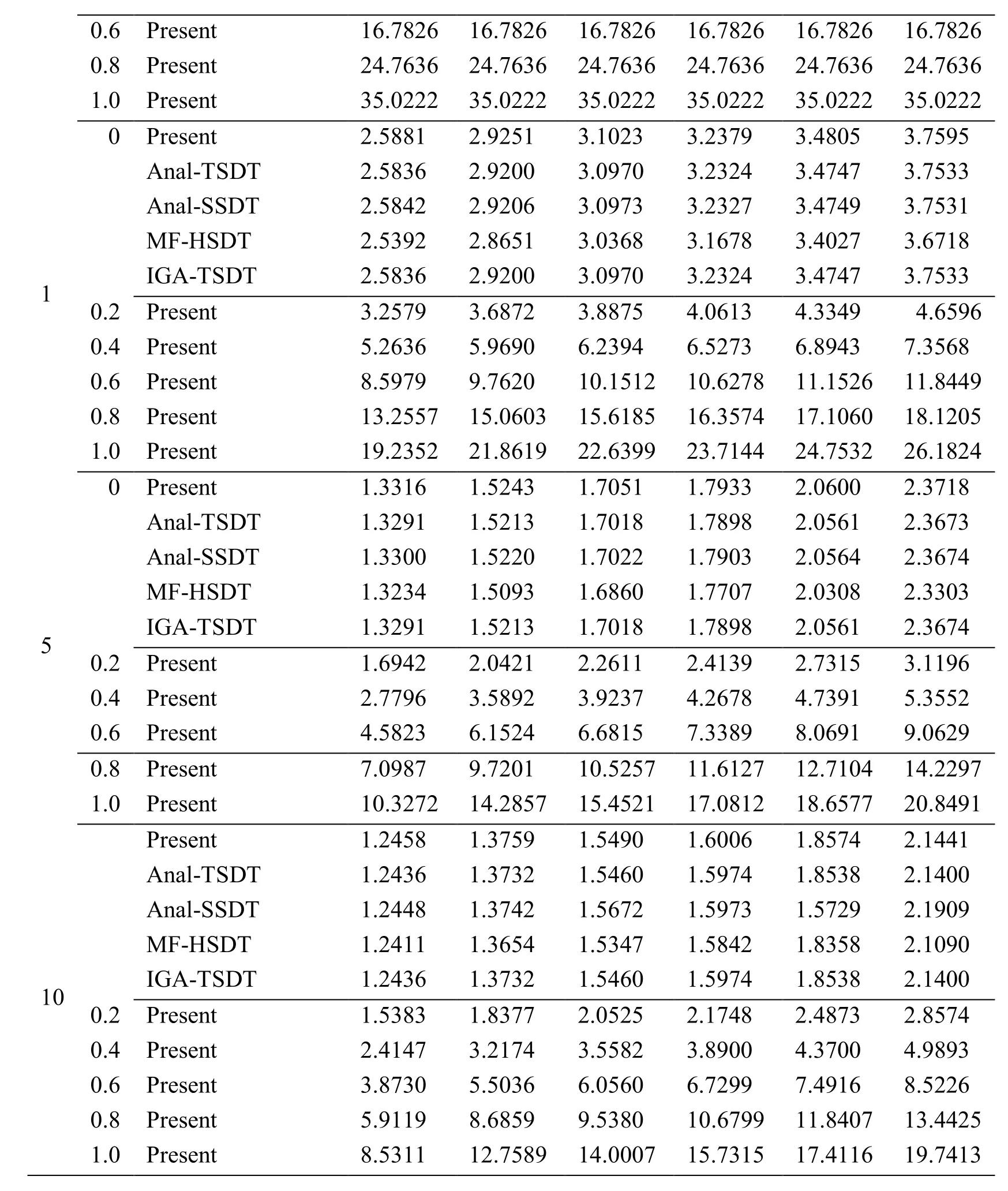
0.6 Present 16.7826 16.7826 16.7826 16.7826 16.7826 16.7826 0.8 Present 24.7636 24.7636 24.7636 24.7636 24.7636 24.7636 1.0 Present 35.0222 35.0222 35.0222 35.0222 35.0222 35.0222 0 Present 2.5881 2.9251 3.1023 3.2379 3.4805 3.7595 Anal-TSDT 2.5836 2.9200 3.0970 3.2324 3.4747 3.7533 Anal-SSDT 2.5842 2.9206 3.0973 3.2327 3.4749 3.7531 MF-HSDT 2.5392 2.8651 3.0368 3.1678 3.4027 3.6718 1IGA-TSDT 2.5836 2.9200 3.0970 3.2324 3.4747 3.7533 0.2 Present 3.2579 3.6872 3.8875 4.0613 4.3349 4.6596 0.4 Present 5.2636 5.9690 6.2394 6.5273 6.8943 7.3568 0.6 Present 8.5979 9.7620 10.1512 10.6278 11.1526 11.8449 0.8 Present 13.2557 15.0603 15.6185 16.3574 17.1060 18.1205 1.0 Present 19.2352 21.8619 22.6399 23.7144 24.7532 26.1824 0 Present 1.3316 1.5243 1.7051 1.7933 2.0600 2.3718 Anal-TSDT 1.3291 1.5213 1.7018 1.7898 2.0561 2.3673 Anal-SSDT 1.3300 1.5220 1.7022 1.7903 2.0564 2.3674 MF-HSDT 1.3234 1.5093 1.6860 1.7707 2.0308 2.3303 5IGA-TSDT 1.3291 1.5213 1.7018 1.7898 2.0561 2.3674 0.2 Present 1.6942 2.0421 2.2611 2.4139 2.7315 3.1196 0.4 Present 2.7796 3.5892 3.9237 4.2678 4.7391 5.3552 0.6 Present 4.5823 6.1524 6.6815 7.3389 8.0691 9.0629 0.8 Present 7.0987 9.7201 10.5257 11.6127 12.7104 14.2297 1.0 Present 10.3272 14.2857 15.4521 17.0812 18.6577 20.8491 Present 1.2458 1.3759 1.5490 1.6006 1.8574 2.1441 Anal-TSDT 1.2436 1.3732 1.5460 1.5974 1.8538 2.1400 Anal-SSDT 1.2448 1.3742 1.5672 1.5973 1.5729 2.1909 MF-HSDT 1.2411 1.3654 1.5347 1.5842 1.8358 2.1090 10IGA-TSDT 1.2436 1.3732 1.5460 1.5974 1.8538 2.1400 0.2 Present 1.5383 1.8377 2.0525 2.1748 2.4873 2.8574 0.4 Present 2.4147 3.2174 3.5582 3.8900 4.3700 4.9893 0.6 Present 3.8730 5.5036 6.0560 6.7299 7.4916 8.5226 0.8 Present 5.9119 8.6859 9.5380 10.6799 11.8407 13.4425 1.0 Present 8.5311 12.7589 14.0007 15.7315 17.4116 19.7413

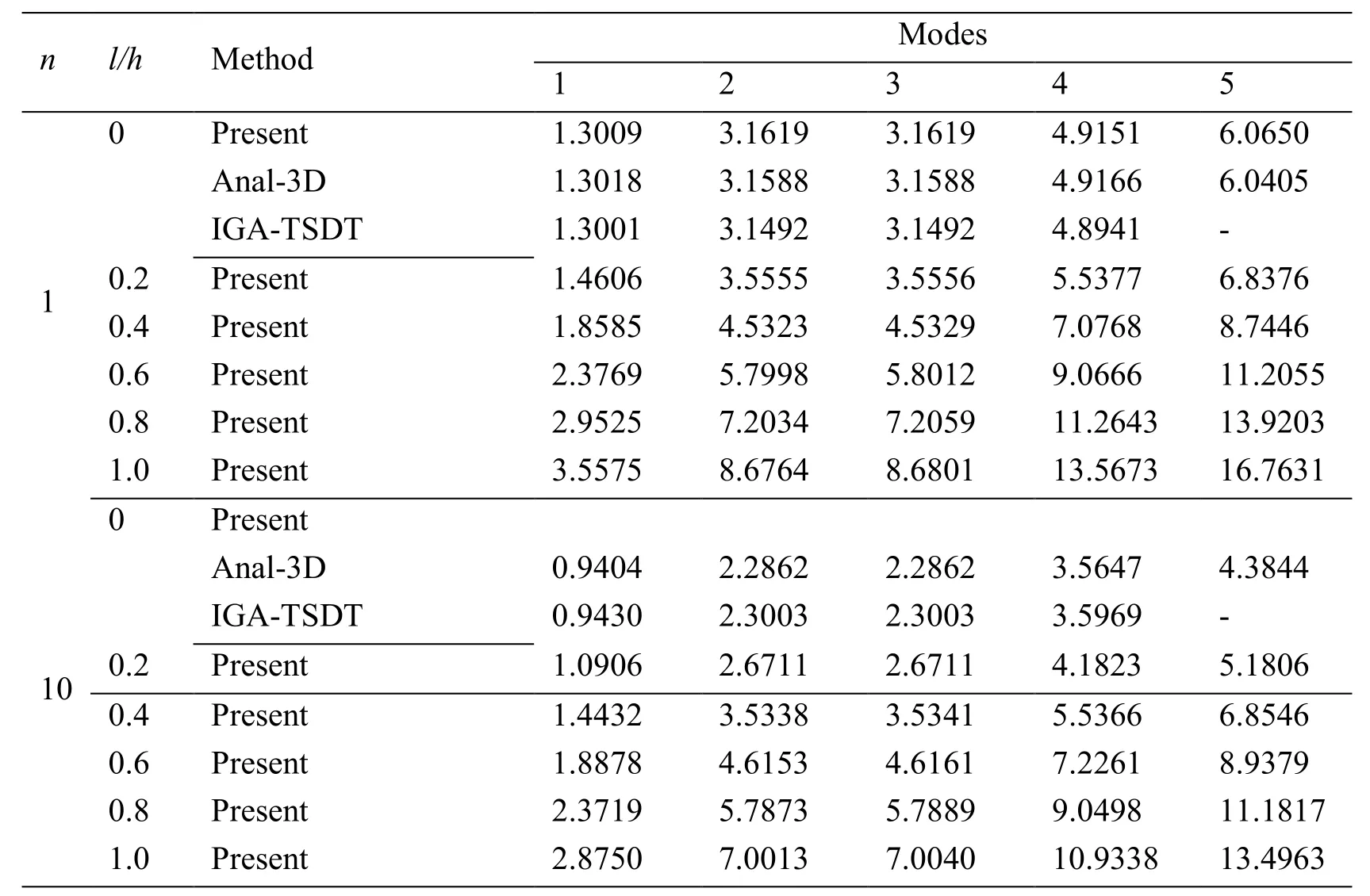
Table 10:The first five non-dimensional natural frequenciesof the simply supported sandwich square microplate with n=1 and h b-h c-h t=2??

n l/h Method Modes 1 2 3 4 5 0 Present 1.3009 3.1619 3.1619 4.9151 6.0650 Anal-3D 1.3018 3.1588 3.1588 4.9166 6.0405 IGA-TSDT 1.3001 3.1492 3.1492 4.8941 -10.2 Present 1.4606 3.5555 3.5556 5.5377 6.8376 0.4 Present 1.8585 4.5323 4.5329 7.0768 8.7446 0.6 Present 2.3769 5.7998 5.8012 9.0666 11.2055 0.8 Present 2.9525 7.2034 7.2059 11.2643 13.9203 1.0 Present 3.5575 8.6764 8.6801 13.5673 16.7631 0 Present Anal-3D 0.9404 2.2862 2.2862 3.5647 4.3844 IGA-TSDT 0.9430 2.3003 2.3003 3.5969 -100.2 Present 1.0906 2.6711 2.6711 4.1823 5.1806 0.4 Present 1.4432 3.5338 3.5341 5.5366 6.8546 0.6 Present 1.8878 4.6153 4.6161 7.2261 8.9379 0.8 Present 2.3719 5.7873 5.7889 9.0498 11.1817 1.0 Present 2.8750 7.0013 7.0040 10.9338 13.4963

5 Conclusion

A size-dependent HSDT meshfree model was presented for bending,free vibration and buckling analyses of FG microplates.The method retained one material length scale parameter and can capture the size effect.Material properties as Young’s modulus,Poison’s ratio and density mass varied the plate thickness according to the rule of mixture.The discrete system equations were obtained by employing the principle of virtual work and the MΚI meshfree method.The present model can degenerate into the classical HSDT model when ignoring the material length scale parameter.For fully clamped boundary conditions,the normal slopes can be directly imposed by allocating zero values to the corresponding displacements at the boundary nodes and its adjacent nodes.By this way,it is not necessary to require additional variables in comparison with the traditional FEM.The effects of geometries,boundary conditions,aspect ratios,power index and material length-scale parameters on the displacement,natural frequency and critical buckling load of isotropic and sandwich FG microplates were studied.Numerical results indicated that a reduction of displacement and an increase of natural frequency as well as critical buckling load within the presence of size effects were conducted.It also shows that the stiffness of FG microplates were raised with respect to an increase of size effects.Besides,the results derived from the present and classical models were almost identical when the plate thickness was much far larger than the material length scale parameter.

Through numerical results,it shows that the present approach provided stable and accurate solutions in comparison with other methods.

Acknowledgement:This research is funded by Ho Chi Minh City Open University under grant number QT-16-1-32.