LCZ序列在多基地雷达中的应用研究
2018-12-26王鹏毅苏卫民
王 钊,王鹏毅,苏卫民
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.南京理工大学 电子工程与光电技术学院,江苏 南京 210094)
LCZ序列在多基地雷达中的应用研究
王 钊1,2,王鹏毅1,苏卫民2
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.南京理工大学 电子工程与光电技术学院,江苏 南京 210094)
正交波形设计一直是多基地雷达中的研究热点。将低相关区间(LCZ)序列引入多基地雷达,以该序列作为发射信号的回波信号与多基地雷达的发射信号进行匹配滤波以后,其相关输出在主峰附近将保持近乎理想的自相关和互相关特性,因此对强多址干扰具有很好的抑制效果。采用交织方法构造低相关区间序列,并给出了LCZ序列在多基地雷达中的应用方法及检测和估计性能的Matlab仿真,仿真结果表明,LCZ序列可以有效地解决多址干扰问题。
多基地雷达;多址干扰;低相关区间序列
0 引言
在双/多基地雷达中,为了获得较高的距离分辨能力,通常需要序列的自相关函数为一个冲击函数。为了抑制多址干扰[1],通常需要序列集的互相关函数值处处为零,寻找低旁瓣且正交性好的码字是双/多基地雷达中需要解决的首要问题[2-3]。
在实际情况中,自相关函数的副峰值和互相关函数的副峰值是一对矛盾,若使一个减小则另一个必然增大,即不存在副峰值处处为零的序列码集,序列集的相关性会受到一些理论界的限制,如Welch界[4]、Sidelnikov界[5]等。m序列[6-7]和Gold序列[8-9]是通信领域常用的2种码型,m序列虽然自相关性好,但是互相关性差,且保密性差,码字数量少;Gold序列虽然具有较好的互相关性能,但是其自相关性较差,保密性也很低,且码集数量也有限。
Fan等人针对准同步CDMA系统,不再要求扩频序列在整个周期内具有理想相关特性,只要求序列在同步误差范围内具有理想相关特性,提出了零相关区(Zero Correlation Zone,ZCZ)的概念[10-11]。稍后,Tang等人推广了ZCZ,提出了低相关区(Low Correlation Zone,LCZ)的概念[12-13]。
LCZ通过不同的构造方法可以获得大量的码集,并且LCZ序列集在相关区之内有着接近理想的相关特性,可见其在双/多基地雷达中的性能明显优于传统的伪随机序列[14-15]。因此,本研究采用低相关区序列作为双/多基地雷达的工作波形,并对LCZ序列与m序列在多址干扰下的目标检测和参数估计性能进行了仿真分析。
1 雷达多址干扰模型
假设多基地雷达的发射基带信号为ui(t),i=1,2,…,P,P为雷达总数。雷达场景中存在匀速运动的单个点目标,信号发射时雷达与目标初始距离为R0i,径向速度为vi,那么第i部雷达的接收基带信号可以表示为:
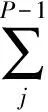
(1)
式中,雷达i的τ0i=2R0i/c为目标时延;fdi=2vi/c为雷达i的多普勒频率;τij=Rij/c为雷达i和雷达j的时延;Rij表示雷达i和雷达j之间的距离;τ0ij=(R0i+R0j)/c为雷达i和雷达j的合成目标时延;fdij=(vi+vj)/c为雷达i和雷达j的合成多普勒频率;c为光速。可以看出,式中第1项为雷达i的有用目标回波,第2项为直达波干扰信号,第3项为其他雷达的多址干扰信号。
对式(1)进行匹配滤波处理,可得
式中,Rii为雷达i的自相关函数;Rij为雷达i和雷达j的互相关函数。式中的直达波干扰信号可以通过多址信号的正交性、空域滤波及频域滤波来抑制,而多址干扰只能利用多址信号的正交性来抑制。这对多基地雷达信号的正交性提出了极高的要求,低相关区序列是一种局部相关特性趋于理想化的序列集。
2 低相关区序列
2.1 基本概念
设U是一个复数序列集,包含的序列个数为M,每个序列周期为N,表示为U=u0,u1,…,uM-1,其中ui=ui,0,ui,1,…,ui,N-1,ui,j=1。
定义两序列ui,uj∈U的周期互相关函数为:
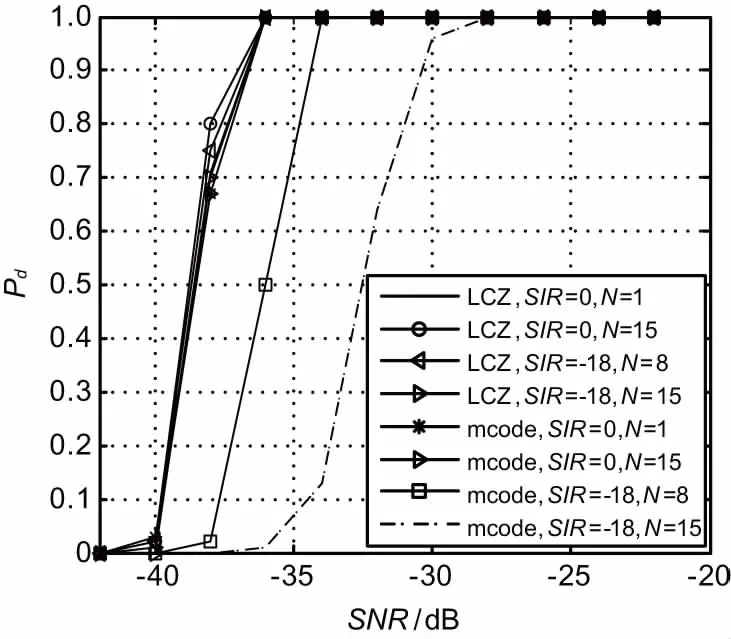
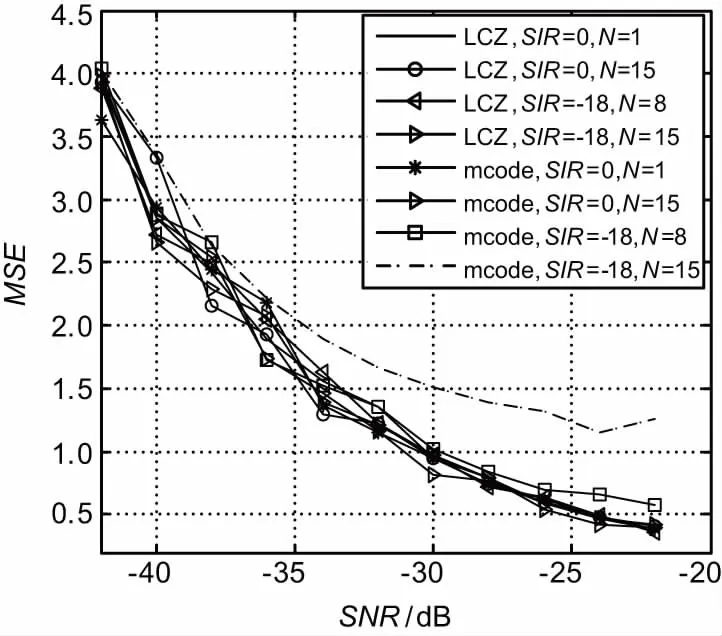
式中,0≤τ 表示取共轭。当i=j时,称为序列ui的自相关函数。进一步得到低/零相关区间序列的定义,设ui,uj∈U,若当τ Rui,uj(τ) ≤δ, 则称U为低相关区间(LCZ)序列,表示为LCZ(N,M,L,δ),其中L表示T时间内的序列长度。当δ=0时,称U为零相关区间(ZCZ)序列,表示为ZCZ(N,M,L)。由于理想的二元ZCZ序列集的数目较少,本课题将采用二元LCZ序列集作为双/多基地雷达的工作信号。 近年来,许多学者提出了构造低相关区序列集的方法,基于GMW序列的构造方法,有限域GF(P)上的渐进最佳的LCZ序列集的构造方法,以及子域分解类的LCZ序列集构造法。但是以上LCZ序列集的构造方法均不能灵活选择序列集的参数。为此又出现分圆类构造法[16]、互补序列对构造法[17]和交织方法的LCZ序列集构造法[18]。其中,交织方法是一类有效的方法,主要是利用移位序列对具有理想自相关的序列做交织运算,然后利用正交矩阵对交织序列进行数量扩展,得到LCZ序列集[19-20]。 设a=(a0,a1,a2,…aN-1)是一个周期为N的序列,ei=(ei,0,ei,1)是长度为2的序列,其中0≤i 将矩阵Ui的每行联接得到序列,可以得到周期为2N的交织序列为: 也可以写为: ui=Sei,0(a),Sei,1(a) = a0+ei,0,a0+ei,1,…,aN-1+ei,0,aN-1+ei,1, 式中,S表示向左循环移位运算,例如Si(a)=(ai,ai+1,…,ai-1)。序列ui就成为交织序列,序列a和ei分别成为交织序列ui的基序列和移位序列。需要注意的是,对于相同的基序列a,2个不同的移位序列ei,ej可能产生2个移位等价的交织序列,因此只有移位序列不等价时构造的交织序列才具备低相关区的特性。这里给出了一种移位序列的构造方法,通过该移位序列构造的交织序列集的个数M接近于N/L。 在雷达应用中,低相关区交织序列的构造步骤可以总结如下: 步骤1:根据多基地雷达的数目确定交织序列集的个数M=「P/2⎤,根据目标的最大距离确定零相关区域为: 式中,「·⎤表示向上取整运算;Rmax为目标最大距离;ts为雷达采样时间间隔。 步骤2:产生数目为M的移位序列集E,并保证任意一对移位序列都是不等价的, E=e0,e1,e2,…,eM-1, 式中,ei=ei,0,ei,1,i=0,1,…,M-1。 步骤3:根据基序列a和移位序列E构造交织序列集U1,可得 步骤4:扩展U1为更大的交织序列集U=U1∪U2,其中U2可以写为: 那么,当基序列a为理想的二值序列时,可以得到LCZ序列集,且参数为(2N,2M,L,2)。 下面将给出数据仿真来验证LCZ序列在雷达应用中的有效性。假设雷达参数设置如下:信号载频f0=10 GHz,带宽B=2 MHz,采样频率fs=4 MHz,探测场景中共存在16部雷达,探测最大距离为 150 km。那么根据上述可得,LCZ序列由15位m序列采用交织方法合成,且低相关区间的码长设置为4 000;与LCZ对比的m序列阶数为16位。 下面分别给出多址干扰信干比为0 dB和-18 dB,多址干扰源数目为1和15时,信噪比对检测和参数估计性能的影响,信噪比取值范围是-43~-22 dB。信干比为0 dB和-18 dB,多址干扰源数目为1和15时,不同信噪比下检测概率的曲线,如图1所示。由图1可以看出,当信干比较高时,此时检测性能完全受信噪比控制,随着多址干扰源数目的增加,检测概率基本不变;当信干比较低时,m序列的检测性能随着干扰源数的增加急剧下降,而LCZ序列的检测性能基本不受影响。 图1 不同信噪比下的检测概率 信干比为0 dB和-18 dB,多址干扰源数目为1和15时,不同信噪比下测距误差的曲线如图2所示。可以看出,当信干比较高时,此时测距性能完全受信噪比控制,随着多址干扰源数目的增加,测距误差基本不变;当信干比较低时,m序列的测距性能随着干扰源数的增加急剧下降,而LCZ序列的测距性能基本不受影响。 图2 不同信噪比下的测距误差 本文给出了LCZ序列在多基地雷达中的应用方法,并对m序列和LCZ序列在多址干扰的抑制效果进行了对比仿真。仿真结果证明,当信干比较高时,目标检测及参数估计的性能完全受信噪比控制,2种信号的检测性能与多址干扰源数目无关;当信干比较低时,m序列的目标检测及参数估计性能随着多址干扰源数目的增加急剧下降,而LCZ序列则保持不变,说明了LCZ序列可以有效地抑制不同雷达站之间的多址干扰。 [1] 楚恒林,范建军,张天桥.多址干扰抑制技术在卫星导航系统的应用研究[J].无线电工程,2015,45(7):50-53. [2] 李学勇.双/多基地雷达发展及关键技术[J].雷达与对抗,2013,33(2):4-8. [3] 狄旻珉,苟彦新.多址干扰对CDMA系统的影响及干扰抑制措施[J].无线电通信技术,2002,28(5):45-47. [4] WELCH L. Lower Bounds on the Maximum Cross Correlation of Signals[J].IEEE Transactions on Information Theory,1974,20(3):397-399. [5] SIDELNIKOV V.On Mutual Correlation of Sequences[J].Soviet Math Doklady,1971,12(1):197-201. [6] DING C S,MOISIO M J,YUAN J.Algebraic Construction of Optimal Frequency-hopping Sequences[J].IEEE Transactions on Information Theory,2007,53(7):2606-2610. [7] DING C S,YIN J X.Sets of Optimal Frequency-hopping Sequences[J].IEEE Transactions on Information Theory,2008,54(8):3741-3745. [8] 郜蓓.扩频码速率异步时直扩系统码分多址能力[J].无线电工程,2014,44(11):30-33. [9] 王玉东,刘春雷.Gold序列互相关性的新证明及非最大Gold序列性质研究[J].通信技术,2014,47(3):241-246. [10] FAN P Z,SUEHIRO N,KUROYANAGI N,et al.Class of Binary Sequences with Zero Correlation Zone[J].Electronics letters,1999(35):777-779. [11] 王扬志,许成谦,李刚.最佳零相关区序列集构造方法的改进[J].无线电通信技术,2013,36(2):16-18. [12] TANG X H,FAN P Z.Lower Bounds on Correlation of Spreading Sequence Set with Low and Zero Correlation Zone[J].Electronics Letters,2000(36):551-552. [13] 唐小虎.低/零相关区理论与扩频通信系统序列设计[D].成都:西南交通大学,2001. [14] 黎薇萍,洪伟,陶海红,等.用于分布式天基SAR系统低速运动目标检测的空时波形优化设计[J].电子学报,2008,36(12):2383-2388. [15] MA C Z,YEO T S,TAN C S,et al.Three-dimensional Imaging of Targets Using Colocated MIMO Radar[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(8):3009-3021. [16] YANG Y,TANG X H,ZHOU Z C.Perfect Gaussian Integer Sequences of Odd Prime Length[J].IEEE Signal Processing Letters,2012,19(10):615-618. [17] APPUSWAMY R,CHATURVEDI A K.A New Framework for Constructing Mutually Orthogonal Complementary Sets and ZCZ Sequences[J].IEEE Transactions on Information Theory,2006,52(8):3817-3826. [18] GONG G,GOLOMB S W,SONG H Y.A Note on Low Correlation Zone Signal Sets[J].IEEE Transactions on Information Theory,2007,53(7):2575-2581. [19] ZHOU Z C,TANG X H,GONG G.A New Class of Sequences With Zero or Low Correlation Zone Based on Interleaving Technique[J].IEEE Transactions on Information Theory,2008,54(9):4267-4273. [20] HU H G,GONG G.New Sets of Zero or Low Correlation Zone Sequences via Interleaving Techniques[J].IEEE Transactions on Information Theory,2010,56(4):1702-1713. ApplicationofLCZCodeinMulti-staticRadar WANG Zhao1,2,WANG Pengyi1,SU Weimin2 (1.The54thResearchInstituteofCETC,Shijiazhuang050081,China;2.SchoolofElectronicEngineering&OptoelectronicTechnology,NanjingUniversityofScience&Technology,Nanjing210094,China) Orthogonal waveform design is a focus area of multi-static radar all the time.In this paper,the LCZ code is introduced into multi-static radar as transmitting signal,after the echo is processed by matched filtering with all the transmitted signals,the output nearby main-lobe retains almost ideal characteristics of autocorrelation and cross correlation.And so,the multiple access interference can be rejected.The LCZ code is generated through interleaving technique,the application of LCZ code in multi-static radar is given,and it is verified by simulation results that the problem of multiple access can be resolved effectively. multi-static radar;multiple access interference;low correlation zone code 2017-09-05 河北省博士后科学基金资助项目(B2016003032) 10.3969/j.issn.1003-3106.2018.01.14 王钊,王鹏毅,苏卫民.LCZ序列在多基地雷达中的应用研究[J].无线电工程,2018,48(1):64-67.[WANG Zhao,WANG Pengyi,SU Weimin.Application of LCZ Code in Multi-static Radar[J].Radio Engineering,2018,48(1):64-67.] TN911 A 1003-3106(2018)01-0064-04 王钊男,(1985—),毕业于南京理工大学通信与信息系统专业,博士,工程师。主要研究方向:航天测控、随机信号雷达目标捕获与跟踪。 王鹏毅男,(1968—),博士,研究员。主要研究方向:测控总体技术研究。 苏卫民男,(1959—),博士,教授。主要研究方向:雷达成像。2.2 交织方法构造低相关区序列集
3 低相关区序列在雷达中的应用
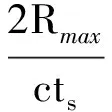
4 结果分析
5 结束语

