循序渐进——数学思维发展的应然选择

江苏镇江市八叉巷小学（212001）

序，即次序、序列、条理。比利时科学家普里戈金曾说过：“一切事物都按照相对有序的状态在发展。”对数学学习来说，有序就是一种按次序、有条理的学习状态。

《义务教育数学课程标准》（2011年修改版）提出：让学生通过观察、实验、猜测、推理、交流、反思等活动，感悟知识的形成和应用。学生学习数学就是积累数学活动经验、发展数学思维、形成数学学习能力的过程，而数学学习离不开有序学习，思维发展的理想状态也应是有序的。

小学生的数学思维是由形象思维逐步向抽象思维过渡的，这就是思维发展的“序”。在数学教学中，教师应循着学生思维的“序”，循着数学知识的“序”，逐渐发展学生的数学思维，培养他们的数学素养。

一、找序：在直观操作中感知“序”

低年级的学生由于年龄小，往往对直观形象的事物比较感兴趣，思考问题时通常只看到事物的表面，这样“浮光掠影”式的学习,不能触及问题的本质。在数学教学中，教师可以借助形象的演示活动引导学生动手操作，通过真实有效的实践活动，使学生的理解由模糊迈向清晰，让学生感知数学知识的“序”，触摸数学知识的本质，从而培养学生的数学思维能力。

例如，在教学“9的分与合”时，教师在讲解“分桃子”的问题时借助学具来演示摆法，让学生自己去发现、思考问题，然后引导学生借助实践操作，理解“9的分与合”的“序”，为后续学习“10以内的加减法”做好准备。

教师依次出示9个桃子和2个盘子的图片，先让学生用学具分一分，把9个桃子分到2个盘子里。接着，教师提问：“这9个桃子可以怎么分？如果让你说出9的所有分法，一个都不能漏掉，你打算按什么样的顺序说？”

学生交流分法。从1开始：9可以分成1和8，2和7，3和6，4和5；也可从8开始：9可以分成8和1 ，7和2，6和3，5和4……

学生的学习不仅是简单的信息积累、获取知识的过程，更是理解知识的意义、构建知识体系的过程。知识的形成过程需要学生的亲身经历。对于低年级学生来说，实践操作是促进体验和内化知识的有效方法之一。在以上教学活动中，教师让学生亲自探索分桃子的方法，把抽象的“9的分成”转化为直观操作，从操作活动的有序到知识理解的有序，为学生呈现真实的探究过程，让他们体会各个知识点的内在联系。

二、循序：在分析推理中明晰“序”

中年级学生的思维仍以具体形象思维为主，但逐步由形象思维向抽象思维过渡。在数学学习中，教师应让学生参与学习的全过程，引导学生通过简单的分析、类比、推理、概括等活动，让学生感悟数学分析的“序”，明晰数学知识的“序”，从而促进学生的思维发展，提高学生的数学素养。

例如，在教学“长方形和正方形的周长”时，教师出示一道习题:你能在方格纸上画出周长是16厘米的长方形或正方形吗？（每个小格子都是边长为1厘米的正方形）

如何画出符合题目要求的长方形或正方形？教师可以引导学生进行分析：由“长方形或正方形的周长是16厘米”，求出长与宽的和是8厘米，然后思考8可以分成几和几即可得出长和宽的长度，由此可画出符合题意的长方形或正方形。这个分析过程就是一个有序思考的过程，让学生明晰分析题意的“序”。

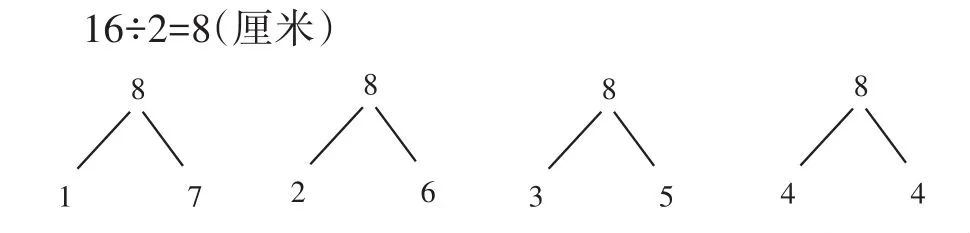
通过分析推理，列式表述思考过程可以更好地培养学生分析和解决问题的能力，将知识碎片整合为系统化、结构化的认知体系，让学生的思维广度和深度得到进一步提升。

三、渐进：在深入理解中表述“序”

数学知识的学习，最重要的是让学生理解知识、积累学习经验、形成数学学习能力。教师应从学生已有的认知经验出发，明确知识源头，思考知识背后的规律，引导学生感悟数学思想和数学方法，并学会通过恰当的形式来表述数学本质的“序”，从而逐步提高学生分析和解决问题的能力。

例如，在教学“分数与除法的关系”时，面临“把3块饼平均分给4个小朋友，每人分得多少块？”的问题，教师从学生的已有经验出发，先引导学生借助3张圆形纸片来“分饼”，再互相交流“分饼”的方法。

师：你是怎么分的？说说你的分法和结果。

生1：把3块饼依次平均分成4份，每次分1块饼的1/4，是1/4块；分了3次，就是3个1/4块，即3/4块。

生2：把3块饼叠在一起平均分成4份，每份是3块饼的1/4，即3/4块。

……

围绕“能不能用分数表示两个数相除的商”的核心问题，以细小问题慢慢地组织学生通过“分饼”理解“3/4块”的含义。把饼抽象成圆，自然而巧妙地借助操作活动使学生完整地经历知识探究的过程，从不同的角度理解分数的意义，不断积累感性经验，丰富数学知识，突破思维的障碍，体会数学思维的有序的表达，从而激发学生的学习兴趣，培养学生自主获取知识的习惯。

四、升华：在知识应用中构建“序”

数学教学应从讲授知识向培养素养转型，培养的应是具有创造力的探究者、创新者。教师应遵循学生的认知发展规律，激发学生的学习动力，使学生成为知识应用的主体，在应用知识的过程中提升创新能力。

例如，在教学“三角形的三边关系”时，教师出示一道习题：小红的身高是1.4米，腿长是0.8米，有人说她一步能走2米，你同意这个说法吗？

生1：我认为小红一步不能走2米，除非是跳。

（教师出示小红走路的图片，引导学生观察、思考）

生2：小红走路时，两腿的长度与两腿间的距离构成了一个近似的三角形。三角形的任意两边之和大于第三边。

生3：0.8+0.8=1.6（米），一步的长度要小于1.6米，所以小红一步不可能走2米。

教师以小红走路的情境为素材，让学生用所学的知识解决生活现象，可真实地反映学生的思维和探究过程，由此培养了学生发现问题、思考问题，并运用所学知识来解决生活问题的能力。

综上所述，在数学教学中，教师应遵循学生认知发展的“序”，把握数学知识的“序”，明晰数学方法的“序”，表达数学本质的“序”，构建数学学习能力的“序”，使课堂成为学生积累数学学习经验的场所。让学生在有序操作、有序思考、有序理解、有序应用、有序学习的过程中，不断提升思维品质，发展数学素养。