以有形材料为根本，激活学生无形思维——“平方数的相差关系”的教学实践和反思

江苏兴化市大邹中心小学（225763）

众所周知，小学生的形象思维能力大于抽象思维能力，如果离开了有形的学习素材，那么培养学生数学思维就成了无本之木。因此，在教学中，教师要牢牢抓住有形的学习素材，引导学生完成外在和内隐的数学思维活动，培养学生的数学素养。下面，以“平方数的相差关系”的教学为例，谈谈具体的操作方式。

一、回顾旧知，激发参与动力

师（出示平方数：32，52，62，352，642，652）：请读一读，并说一说这些数字的含义。

师（揭示课题，出示例子“52-22”）：两个平方数之间加一个减号，那么这个平方数就建立了相差关系。

师：想一想，我们曾经学过哪一个知识点是将两个完全相同的数相乘，得到的积就是结果呢？

通过启发，学生很快想到求正方形的面积就是边长乘边长，即两个数相乘。由此，教师就可引导学生探索平方数的相差关系。

二、展开新知探究，引导概念建构

1.借助格子图，直观感知

师（出示一张格子图，如图1）：仔细找一找，你能看出4的平方和3的平方的差别是怎样的吗？把相差的部分涂上颜色。

图1

学生的作品：

图2

2.自主探索

师（出示几组具有相差关系的平方数：52-32，72-42，42-32，652-352）：选择其中1到2个算式，在对应的格子图中表示出这两个平方数相差的关系，并用颜色涂出这两个平方数相差的部分。根据等级变形的规律，运用平移、割补等方法，把两个平方数相差的部分转化成为规则图形，并用示意图表示出来，最后再用一个算式表示。

3.成果交流

学生探索成果（如图3所示）：

图3

（学生分组讨论，说出自己的设计意图）

三、引导学生自主感悟数学规律

呈现成果：

图4

师：在这些等式中，你有什么发现？

学生发现规律：

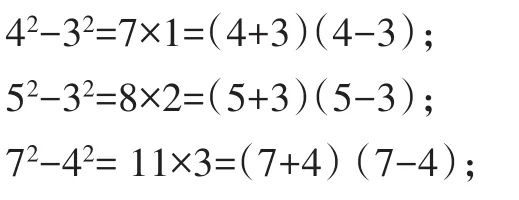
师：你能结合图片说出等式左右两边式子中数据之间的内在联系和规律吗？（如图5）

图5

师：这些数字可不可以用字母表示？

生：大正方形的边长用字母a表示，小正方形的边长用字母b表示，这样就可以把这些算式用一般的字母形式表示出来，得到

a2-b2=（a+b）（a-b），如图6所示。

图6

【教学思考】

对于小学生来说，在进行数学思维活动时，由于形象思维发展早于抽象思维的发展，因此，需要一些有形的数学信息来作为支撑。因此，在教学中，笔者以有形的学习材料作为根本，激活学生的数学思维。

1.数形结合，提供“可视化”的观察信息

笔者在这一课中，进行了分层设置，为学生提供“可视化”的观察信息：第一个层次，在黑板上出示几组具有相差关系的平方数，然后要求学生进行自主选择后展开探索。学生借助格子图这个直观几何图形，就能够用算式（数）来表示相差部分的大小，由此将数与形有机结合起来，为进一步理解平方数的相差关系做好了铺垫。第二个层次：将学生的图示作品展示出来，分小组进行讨论交流。在这个交流的过程当中，学生都获得了有形的信息材料。另外，学生通过展示作品，交流讨论，就能够用完整的语言将自己的选择和探索的过程，以及结果表达出来，由此提升了学生的数学思维。第三个层次：将学生的作品完整呈现并进行梳理，能够让学生获得完整的有形信息材料，为下一步深入探索并总结规律做好准备。

在这个教学过程当中，通过给学生呈现“可视化”的数学材料，让学生由此展开自主探索和思考，从而打开数学思维之门。

2.立足感性，设置“可比较”的材料

有比较才有区别，“可比较”的材料能够帮助学生的思维层层递进，节节攀升，因此，教师要设置“可比较”的教学素材，给学生提供有效的信息作为比较载体，带领学生展开自主探索和思考。

我在这一课中进行了如下设置：其一，先给学生呈现自主探索的活动成果，让每一个学生能够获取直观的感知；其二，让学生借助观察和思考，发现这些可视化信息背后的规律，有了这些直观的形象材料，就激发了学生抽象概括平方数相差关系这一内在规律的动力；其三，对比有形的感性材料，抽象出数学规律。

有了“可比较”的材料，学生就有了充足可靠的有形材料的感性支撑，也就能够深入数学活动之中，获得有效的抽象思维的发展。

3.分层活动，完善“可概括”的条件

学生数学概括能力的培养是建立在充分的数学活动的基础之上的，因此，教师要给学生提供自主探索的数学活动，帮助学生完善概括所需的条件，促进学生进行有效的概括。

在这一课中，我将学生自主感悟平方数相差关系的规律的数学活动分成了四个层次：层次一，直观呈现学生的成果，提供丰富的感官材料；层次二，引导学生观察，自主探索平方数相差关系的一般性规律；层次三，让学生借助数形结合的规律进行比较，让平方数相差关系的一般性规律更加直观形象；层次四，引导学生概括，在比较化的感性认知下，抽象出平方数相差关系的一般性规律。

学生数学思维的提升是层层递进、步步向上的。学生只有通过几组不同的学习活动，获取有形的成果材料，同中求异，异中求同，才能促进思维品质和数学素养的提升，这也是完善学生“可概括”条件的关键所在。

4.深入经历，把握“可抽象”的时机

对于小学数学来说，抽象是学习活动的最高阶段，其中所经历的过程，也正是学生在数学活动过程中经验积累、水到渠成的一个过程。

在这一课中，我为了让学生能够抽象出一般性的数学规律，特意让学生深入数学探究活动过程中，在学生经历了信息感知、自主观察、对应互联三个层次的经验积累之后，就可顺势让学生抽象出平方差公式。在这个过程中，学生的思维经历了从特殊到一般的过程，也经历了一次完整的数学归纳过程，学生的思维逐步走向丰富和深刻。