透过现象梳缘由 追根溯源理成因——圆的周长与面积的计算错例成因溯源

安徽滁州市湖心路小学（239000）

“圆的周长与面积的计算”这部分内容的学习过程是学生对于“圆”的认识从定性观察、研究到定量观察、研究的跨越过程。对于这部分知识的教学，教师经常会遇到这样的问题：学生会说图形的基本特征，会记和背相关的计算公式，但在具体的应用过程中还是会出现这样或者那样的错误。此时，教师是抱以“熟视无睹”的态度，还是停下追赶教学进度的步伐，静心反思？答案当然是后者。错误的产生暴露了学生的思维过程，反映了教师教学过程中的纰漏，因此，课堂中生成的错误资源是教学中最应把握的关键点，值得师生共同反思错误根源，找到解决问题的策略。下面笔者结合实际教学中的一些典型错例，浅谈自己的几点认识。

一、直面现象梳缘由

[典型错例 1]

求出图1中图形的周长。

图1

[分析与诊断]

产生这种错误的学生不在少数，而且这种错误总是不能根除，这次因教师提醒避免了错误，下次没人提醒了，同样的错误又发生了。仔细分析，这并不是简单的粗心所能解释的。究其原因，一是学生对于周长的概念理解不透彻；二是学生受面积计算的影响，产生错误的知识迁移，计算半圆周长时用整圆的周长除以2。

[典型错例 2]

求出图2中图形的周长和面积。（单位：m）

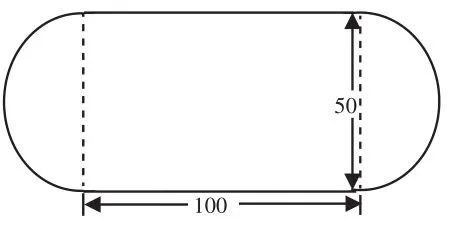
图2

生1：面积是3.14×25×25+100×50。

师：你这样做的理由是什么？

生1：用圆的面积加上长方形的面积。

生2：周长是3.14×50+（100+50）×2。

师：你是怎么想的呢？

生2：用圆的周长加上长方形的周长。

[分析与诊断]

首先，在计算组合图形的面积和周长时，大部分学生更倾向于计算它们的面积，这是因为小学生以直观形象思维为主，对于直接相加的面积计算更容易理解。周长计算出现错误，则是因为学生再次受到面积计算负迁移的影响，想当然地认为圆的周长加上长方形的周长就是组合图形的周长。对此，教师只需让学生对照图形指一指这个组合图形的周长，便能得到很好的解决。

[典型错例 3]

在直径为6米的圆形花坛外围铺一条宽1米的小路，小路的面积有多大？

错误一：3.14×（8×8-6×6）。

错误二：3.14×（7×7-6×6）。

错误三：3.14×（6×6-4×4）。

……

原本以为，学生学完“圆环的面积”这一知识之后，只要给出圆环面积的计算公式，找到大圆半径与小圆半径，他们就可以直接用公式进行计算了。让人难以想象的是，这不算难理解的一道题，为什么做对的学生仅占班级总数的17.6%？这个偏低的百分率引起了我的思考：学生的问题到底出在哪？

[分析与诊断]

新课结束后，学生确实记住了计算公式，但从学生的错误看来，不仅仅是审题不仔细这么简单。虽然学生能记住环形面积计算公式，但是解决具体问题中出错的点却是弄不清大圆和小圆的半径到底是多少。如果本题借助几何直观，图文并茂，学生是很容易看出大、小圆的半径各是多少的。由此可见，学生在脑中将文字转化为图形时，出现了偏差，教师在教学时就要先引导学生将抽象的文字转化成正确的图形，从而准确解决问题。

[典型错例 4]

一台压路机滚筒长2米，直径为1.6米，如果它每分钟滚动10周，一分钟能前进多少米？压路面积是多少平方米？

错误一：一分钟前进的米数是1.6×10。

错误二：压路面积是3.14×0.8×0.8×2×10。

[分析与诊断]

遇到这样的题，做对的学生寥寥无几，学困生根本是无从下手。小学生以形象思维为主，对于题目中的动态运动过程，他们很难将其“静止”，更不要说清晰明白所要解决的问题与动态过程中的哪些量有关。在教学中，教师就要先引导学生想象出“一分钟能前进的米数”与“压过面积”分别指的是什么，再在实际教学中将“动”转化成“静”，促使学生感知转化前后的数量关系。

二、梳理对策研教学

1.注重首次感知

尽管错误、混淆、干扰出现在后续的学习（圆周长、面积的计算）中，教师仍然不能轻视先前的学习，尤其是首次教学周长和面积的概念时，要力求给学生留下正确、鲜明和深刻的印象，以发挥“先入为主”心理定式的积极作用。

在教学“周长”这一概念时，可以让学生先说说对字面意思的理解，然后结合多种图形再指一指，数形对比中，学生的理解也就精准了。正如华罗庚所说的“数缺形时少直观，形少数时难入微”。

2.注重体验感悟

教学前的学情分析尤其重要，教师必须顺应小学生的思维是由形象到抽象的发展规律，放手让学生动手操作，教师只需适时点拨，让其明白：无论是在学习新知时，还是在解决问题时，运用“转化”的数学思想能将未知的转化成已知的，从而解决问题。在教学中，先让学生动手量也好，数也罢，皆符合“数来源于数，量来源于量”。

3.注重比较辨析

学生在探究新知的过程中，除了必要的动手、动脑，更重要的是，在教师的引导和组织下对某一知识点进行辨析。理越辩越明，道越论越清。在辨析的过程中，很容易就能将难点和重点内化、升华，课堂不失精彩，学生兴趣浓厚，教师又何乐而不为呢？

针对面积与周长的错例，还得让学生去反思，错误的“反刍”作用非同一般，它能使数学重难点的教学迎刃而解。

4.注重还原建模

“典型错例4”恰恰体现了数学与生活的紧密联系。数学来源于生活，可是如何将生活中的实际问题再次回归到数学的数量关系中，就得靠学生深厚的数学理解能力及精准的抽象思维能力。教师要引导学生先将“动”转化为“静”，再联系“静”提炼出其中的数量关系，还要唤醒学生的求知欲望，带领学生解决生活中的数学问题，建立学好数学的自信，提高解决问题的能力。

三、启发领悟理成因

课堂是学生出错的地方，在大班化的教学中，学生的错误更是形形色色。学生一旦产生错误，教师不能一味地训斥，而应该站在研究者的高度审视错误，追根溯源，然后找准对策，因势利导，使教学少走弯路，提高教学效率。

1.课前精心预设

课前，教师要充分估计学生可能会产生的各种错误，从而做出种种预设。学生容易出错的地方往往是一堂课的重点或难点之处，因此教师必须精心钻研教材，研究学生可能会产生哪些错误，然后根据学生已有的知识结构精心设计教学过程，针对学生容易出错之处精心设计行之有效的练习，使概念、定义、公式等新知在第一时间“先入为主”，为学生的后续学习打下扎实的基础。

2.课中捕捉时机

学生在学习过程中经常会产生许多意想不到的错误。如何利用好这些错误资源，化弊为利，是每个教师应该考虑的问题。这就需要教师具有良好的教学机智和课堂灵活应变的能力，只要能将学生的错误处理得当，就能获取事半功倍的教学效果。

3.课后分析诊断

对于错误，要先查找原因，方能“对症下药”。教师可将学生的各种错误加以整理、归类，并记载成册，形成易错题库或“诊断卡”，以便下次教学或其他教师在教学研究同一内容时做参考，形成丰富的教学资源。总之，教学过程一定要从学生已有的知识起点和能力基础出发，这样的教学才是有效的。

大道至简，学生是学习的主人，研究学生的错误就是在“读”学生。正如朱德江老师所说：“感悟学生、读懂学生是教学的基础。”对于学生的错误，教师应带着积极的态度去分析原因，以研究错误为契机，时刻把握学生的掌握程度，及时调整教学、改变教学策略，切实提高课堂教学的实效性。