装配式建筑施工塔机吊装就位控制精度的研究
2018-12-26邵新阳马溢坚
邵新阳,马溢坚
(浙江省特种设备检验研究院,浙江 杭州 310020)
装配式建筑建筑即预制装配式混凝土结构建筑(简称PC建筑)是将组成建筑的构件部分或者全部构件在工厂预制加工完成,然后运至施工现场进行组装,是一种模数化、集成化、组装化建筑生产模式。与传统建筑方式相比,装配式建筑建筑有利于提高施工质量、加快工程进度、节约资源、文明施工及环境保护等诸多优点,因而在建筑行业得到了越来越广泛的应用。然而,考虑到用于装配式建筑施工的塔式起重机起升机构需要频繁的启制动并且在复杂的工况下精确就位对孔,目前的塔机起升机构大多仍是采用多速机构或绕线电机串电阻进行有极调速的方式,在进行低速定位时,由于采取的是“倒拉反接制动”的方式运转,转子系统串联大电阻,进而造成机械特性发软的情况,最终无法有效进行低速定位工作,最低运行速度5~8m/min,点动移距离2~20mm,完全不能满足装配式建筑施工钢筋孔对装的要求。
1 变频调速控制系统设计
通过异步电动机转速公式n=60f(1-S)/P可知改变电动机极对数P、转差率S和电源频率f可以调节电机转速。传统调速方式调速范围宽度窄且只能实现有级调速,随着我国电子科技的迅速发展,极大得推动了交流电机无级调速和交流变频系统的发展。本文中塔机起升机构电机速度控制闭环系统如图1所示,给定电机速度与反馈的实际速度差值为速度误差,通过PLC控制器计算生成控制量,并将其传送至变频器控制系统,从而更好地调控电机运转速度,实现闭环控制。然而塔机是一种在复杂多变工况下工作的工程机械,起升机构升降过程受载重的摆动、机械本体的振动和滞后等主要原因,尤其是在外界风力、压力负荷等因素出现转变情形下,传统的增量式PID控制不具备自适应的调整能力,仍不能满足装配式建筑施工中塔机精确就位的要求,故本文提出一种基于模糊控制理论的模糊PID控制器,具有很强的自适应能力,能够满足装配式建筑施工中各种复杂工况下的就位精度要求。

图1 电机速度控制系统
2 模糊PID控制技术
由于操作人员经验不足等原因,在操控工作中,各类信号和有关评价指标不易获取,所以模糊理论,是妥善解决这一问题的主要方式,因此有关操作人员,在正常操作过程中,通过模糊理论,将操作要求、操作数据通过模糊数集进行体现,并将这些模糊集管理规则以及评价指标等有关数据,纳入到计算机知识库系统中进行保存,然后在根据控制系统的实际反应状况,通过模糊推理,实现对PID参数的优化和调整,这就是所谓的模糊PID控制技术。
模糊PID控制器输入变量主要包括偏差变化率ec以及偏差e,而该基础就是通过模糊运算,分析e、ec等参数之间的联系,同时在运算过程中,通过检测得出e、ec,并在模糊控制理论引导下,对有关参数进行调整,从而满足e和ec等参数间的控制要求。自适应模糊PID控制器内部构成以及操作系统如图2所示。

图2 自适应模糊PID控制结构
2.1 模糊控制器的设计
模糊控制器设计工作,主要由模糊规则的制定、模糊推理、去模糊化及算法等部分构成。
2.1.1 输入变量及输出变量的模糊化
输入变量e、ec和输出变量Δkp、Δki、Δkd相对应的模糊语言变量为E、EC、Δkp、Δki和Δkd,设其离散模糊论域都为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}。根据实际操作经验可得, 的基本论域为(-6,6),则量化因子ae=6/6=1,计算公式e(t)=r(t)-y(t),r(t)为系统设定值,y(t)为测量值;ec的基本论域为(-0.3,0.3),则量化因子ace=6/0.3=20;计算公式ec(k)=e(k)-e(k-1);Δkp基本论域为(-10,10),则量化因子akp=6/10=0.6;Δki基 本 论 域 为(-0.2,0.2),则量化因子aki=6/0.2=30;Δkd基本论域为(-1,1),则量化因子akp=6/1=6。
将(-6,6)范围内的参数变量,划分为不同的等级级别,且每个等级都可以视作单个的模糊变量,并组成一个系统、完整的模糊子集,可以分为正小(PS)、正中(PM)、正大(PB)、零(Z0)、负小(NS)、负大(NB)、负中(NM)7个不同等级,各模糊子集的隶属度如表1所示。

表1 e、ec和Δkp、Δki、Δkd的隶属度规则表
2.1.2 设计规则
当e和ec不同时,系统中被控过程对Δkp、Δki、Δkd三参数的自整定要求规定如下。
1)当e较大,为获得更优越的快速跟踪性能,并考虑到偏差e的提升可能造成微分过大,甚至超过可控制范围,因此应当取较大值kp或较小值kd。此外,为了将e控制在合理范围内,减少其因超过一定范围,造成无法调控,因此采取限制积分的方式,此时取ki=0。
2)当e和ec都为中等程度的值时,为尽可能地减少系统的超调量,kp、ki以及kd值也应当控制在一定范围内,而ki应取值较小,kp以及kd也应取中等大小的值,确保系统的快速响应,其中kd的取值影响最大。
3)当e取值较小时,为保证能够在稳定状态下运行,kp、kd取值较大,此外,为了减少系统在靠近预设值时的震动,保证系统的稳定运行,提升系统的抗干扰能力,kd取值应遵循这样的规定:如果ec取较小值,kd取中等值;而ec较大时,kd应取较小值。
4)ec则是表征偏差变化速率快慢的物理量,ec取值越大,kp取值越小,ki则取较大值。
2.1.3 模糊推理规则及解模糊算法
通过公式(1)以及式(2)的输入输出计算方式进行去模糊化的计算,或者用如式(3)的精度较高的公式,具体去模糊化规则如下。
规则1:IFA1ANDB1THENC1
规则2:IFA2ANDB2THENC2
………………………
规则n:IFAnANDBnTHENCn
输入x0ANDy0结论z0
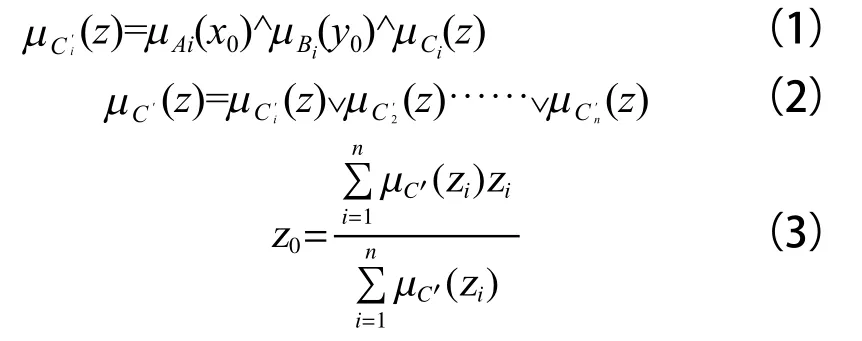
由前提“x0ANDy0”以及有关的模糊规则,“AiANDBiTHENCi(i=1,2,...,n)” 可 计 算 出激活后单条输出模糊变量以及模糊子集C′i,计算公式为(1),而总激活规则的模糊子集C′以及模糊变量公式为(2),模糊变量输出公式为(3)。
在日常应用过程中,因根据输出模糊控制规则、模糊推理原则以及去模糊化重心法等放手,获取模糊控制表,其是在e、ec等领域中元素组合计算得出的控制变量,并在矩阵实验过程中获得修正和调整,并将其保存于计算机系统,在在运算过程中奖特定速度和反馈速度之间的偏差e以及偏差变化率ec值,转换到各自领域中,并根据模糊控制表以及输出变化表,调整PID参数。通过控制查询表,计算在线控制量,从而满足实验所要求。如图3所示。本文模糊控制阀以及自适应PID控制计算法如图4所示。
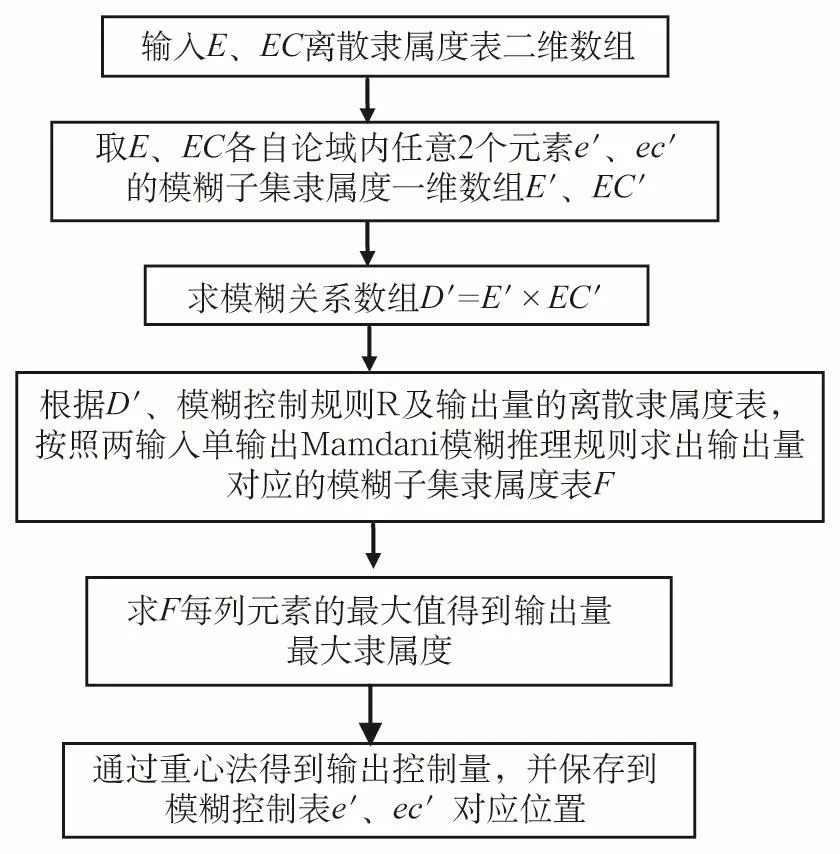
图3 模糊控制表的某一元素值生成流程
3 结 语
利用Matlab软件中的SIMULINK模块进行系统仿真,通过对该系统参数的不断调整,当变频器和异步电动机共同作用的传递函数为20/(S2+3.6S+1)时,e、ec和u分 别 取 0.4、0.2和20,得到的仿真结果比较理想,如图5为系统仿真得到的阶跃响应曲线,由此可知模糊PID控制调节时间较短且响应具有较小的超调量,能够实现塔机运行的精确就位,满足装配式建筑施工中准确对孔的要求。若实际工况中对仿真结果不满意可以通过调整该3个参数获得较为满意的结果。
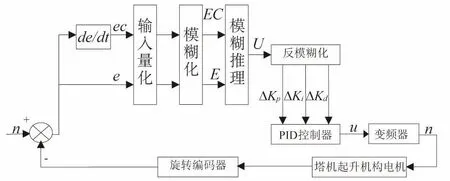
图4 模糊PID控制总体结构
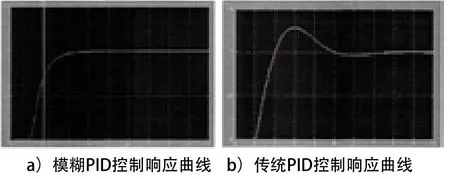
图5 系统修复阶断响应曲线
