基于多特征融合的鲁棒目标跟踪算法

王有豪, 唐 垚, 王彦本

(西安邮电大学 通信与信息工程学院，陕西 西安 710121)

刑事侦查(以下简称刑侦)现场勘验(以下简称现勘)是为发现和收集证据而对案件有关的场所、物品等进行的勘察和检验[1]。视频监控系统是侦查嫌疑人活动轨迹的主要途径，通过视频监控系统可以动态地跟踪目标，结合现场调查、科学分析来确定嫌疑人的轨迹。高效的视频目标跟踪系统对刑侦现勘具有重要意义。

利用视频监控实施目标跟踪会遇到场景中光照变化、相近颜色干扰、目标形变、遮挡等问题[2]。颜色作为描述目标的一种主要特征，对部分遮挡、形变以及旋转都有较强的适应性[3]，但在复杂的场景中，仅使用单一的颜色特征通常很难获得好的效果，对基于多特征融合的目标跟踪算法的研究成为近年来的热点。

文献[4]提出了一种新的颜色特征，将红、绿、蓝3种颜色细化为11种。文献[5]通过使用高斯核计算相邻2帧之间的相关性，取响应最大的点为预测的目标中心。文献[6]提出了一种多目标跟踪算法。文献[7]提出了一种局部二值模式(local binary pattern, LBP)纹理描述算子，它具有光照和旋转不变等优点，且计算复杂度小、识别能力强，已被广泛应用于目标跟踪、图像分割、图像检索等领域。文献[8]中利用LBP算子提取目标区域纹理特征并与颜色特征相结合，实现了基于自适应均值漂移算法的目标跟踪，但是，当场景中存在干扰时，会跟踪失败。文献[9]结合了LBP纹理特征与颜色特征，并将它们应用于粒子滤波。文献[10]认为现有的LBP算子仅将模板中心像素作为阈值，忽略了局部像素之间的相关性，导致所提取的纹理特征缺乏稳健性，易受噪声干扰，因此提出了一种全局二值模式(global binary pattern, GBP)纹理描述算子，它使用模板邻域像素的均值作为阈值，在一定程度上弱化了噪声对纹理的影响。

图像中的噪声主要是脉冲型噪声，中值滤波在抑制脉冲型噪声方面优于均值滤波[11]，它可以在消除噪音的同时保护图像的纹理和边缘。

为了准确地跟踪视频监控系统中嫌疑人的活动轨迹，本文拟提出一种基于多特征融合的鲁棒目标跟踪算法。该算法首先使用中值和均值滤波后的改进全局二值模式(improving global binary pattern, IGBP)纹理描述算子充当线性平滑滤波器，将去除模板幅值序列中最大值和最小值后剩余像素的均值作为阈值，从图像中去除非相干细节，消除偶然的脉冲型噪声，以保持清晰的边缘信息；其次，提取目标区域的颜色特征作为第二种特征，并采用基于不确定性度量的多特征融合策略[12]，在粒子滤波器框架中，融合了改进的纹理特征和颜色特征，通过每种特征的不确定性大小自适应地调整其对跟踪结果的贡献；最后，在跟踪过程中，通过计算在短时间内发生的形变程度来确定目标是否被遮挡，从而采用不同的更新策略对目标模板进行更新。

1 粒子滤波与特征不确定性

1.1 粒子滤波跟踪框架

为了定义贝叶斯跟踪问题，设时刻t的目标状态

xt=ft(xt-1,ξt)。

(1)

其中，ξt是过程噪声。

跟踪的目的是获取t时刻目标状态xt的观测值

zt=ht(xt,et)。

(2)

其中，et是时刻t的观测噪声。

定义{ξ1t}、{e1t}分别为过程噪声序列和测量噪声序列。假设{ξ1t}、{e1t}分别为独立同分布的噪声序列，且两噪声序列和初始状态彼此相互独立。

从贝叶斯估计角度，跟踪问题就是根据给定观察序列{z1t}递归估计目标状态{xt}，即构造目标状态的后验概率分布P(xt|z1t)。求解过程可由以下2部分完成。

(1)预测过程

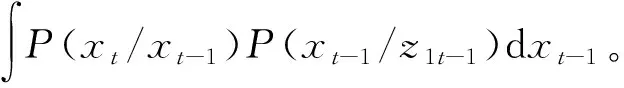
(3)

(2)更新过程

(4)

对于非线性、非高斯的动态系统，式(3)和式(4)的积分是无法解析计算的[13]。粒子滤波是基于序列蒙特卡洛和递归贝叶斯的估计方法[14]，它将积分运算转化为有限样本点的求和运算，即后验概率分布P(xt|z1t)可近似表述为

(5)

假如粒子从重要性分布q(xt,j/xt-1,jz1t)中采样得到，则递归贝叶斯过程可看作如下权值更新过程

(6)

选取先验分布P(xt/xt-1)作为重要性采样函数，则权值更新过程式(6)可以简化为

ωt,j∝ωt-1,jP(zt/xt,j)。

(7)

1.2 特征不确定性

在对不同场景中的目标进行跟踪时，纹理和颜色特征对于目标所在位置估计的准确度有所差异。对于改进后的纹理和颜色特征在目标跟踪过程中的不确定性，采用特征不确定性度量理论[12]来进行计算，设在t+1时刻，第i种特征的不确定性

(8)

(9)

其中，p(zi|xj)表示观察到的第j个粒子上第i种特征的概率值。

由式(8)可知，在特征不确定性的计算过程中，包含所有粒子的空间位置信息和特征观测概率值的熵。在t时刻，如果空间中粒子分布越集中，则σt越小，此时说明该种特征具有较小的不确定性。同样地，H(pi)越小，代表此种特征的观测概率值仅集中在少数的粒子上，则该特征在对于目标位置的估计中有较高的准确度，即不确定性越小。

2 多特征融合的目标跟踪算法

首先，分别给出目标改进纹理特征和颜色特征的提取方法，以及2种特征下目标模板与候选模板相似度的计算方法，并由此给出特征融合策略。其次，判断目标是否发生遮挡从而采用不同的模板更新策略。最后，在粒子滤波框架中给出算法的具体实现步骤。

2.1 图像特征的提取

2.1.1 图像纹理特征的提取

结合均值与中值滤波，提出IGBP纹理描述算子。具体做法为，首先对模板进行绝对值做差处理得到一个幅值序列，然后去除模板幅值序列中的最大值和最小值，取剩余像素的平均灰度值作为阈值。若邻域像素大于此阈值，则取1，反之取0，再与相同大小的权重模板进行卷积，从而得到改进后的纹理特征。定义IGBP算子

(10)

其中，r=1,2,…,Q表示邻域中的第r个像素；Q表示模板中去除中心像素后剩余像素的个数；gr=|dr-dc|表示经过绝对值做差后的灰度值幅值序列，其中，dc表示模板的中心像素的灰度值，dr表示第r个像素的灰度值；阈值gc是去除幅值序列中最大值和最小值后剩余像素的平均灰度值。s(x)是一个二值函数

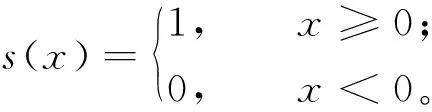
(11)

LBP计算过程中邻域像素权重值和位置固定，这会导致提取的纹理特征对方向十分敏感。因此，采用旋转不变性，即模板邻域连续旋转，取最小值作为IGBP纹理[16]，即

IGBP=min {ROR(IGBP,r)|r=1,2,…,Q}。

(12)

其中，ROR(x,r)表示对得到的二进制数x进行向右循环移位r次。

IGBP算子描述纹理的结构信息，对于纹理的强度用局部反差(LC)算子来描述，局部反差算子

CL=s1/n1-s2/n2。

(13)

其中，s1表示上述模板幅值序列中所有大于阈值gc的像素之和，n1为对应的大于阈值gc的像素个数；s2表示模板幅值序列中所有小于阈值gc的像素之和，n2为对应的像素个数。

本文将IGBP算子与LC算子相结合，使其可以同时描述目标区域纹理的结构和强度。IGBP算子和LC算子的计算原理，如图1所示。

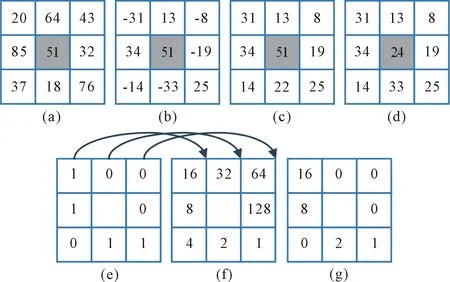
图1 IGBP和LC算子的计算原理

图1(a)表示原始模板，其大小为3×3，灰色部分为模板中心像素；图1(b)表示模板(a)中周围像素与中心像素经过做差后得到的模板序列；图1(c)表示对模板(b)取绝对值得到模板幅值序列；图1(d)表示去除模板幅值序列(c)中最大值和最小值后，取剩余像素的平均值作为模板的中心像素，即阈值；图1(e)表示对模板(d)中周围像素大于阈值的位置取1，否则取0，得到一个二进制序列；通过不断旋转模板(e)，从而得到其对应的最小二进制序列“00011011”；图1(f)表示(e)中每个位置上的权值；图1(g)表示模板(e)、(f)对应位置的乘积，再对(g)求和从而得到IGBP值，即

IGBP=16+8+2+1=27。

对于纹理的强度，由模板幅值序列(d)可知阈值为24，则s1等于所有大于阈值的像素之和，即31+34+33+25，n1为4；s2等于所有小于阈值的像素之和，即14+19+8+13，n2为4，则CL=(31+34+33+25)/4-(14+19+8+13)/4=17.25。

图像目标区域、目标区域的LBP和IGBP纹理，如图2所示。

图2 目标区域的LBP和IGBP纹理

从图2中可以看出，相比于LBP算子，本文提出的IGBP算子对纹理结构信息的描述更加清晰、完整。

IGBP与LC的联合概率分布用于描述目标区域的纹理特征。为了降低计算复杂度，同时考虑纹理的可区分性，当模板大小为3×3时，Q=8，旋转不变仅有36种可能，此时的IGBP与LC算子联合概率分布直方图，如图3所示。

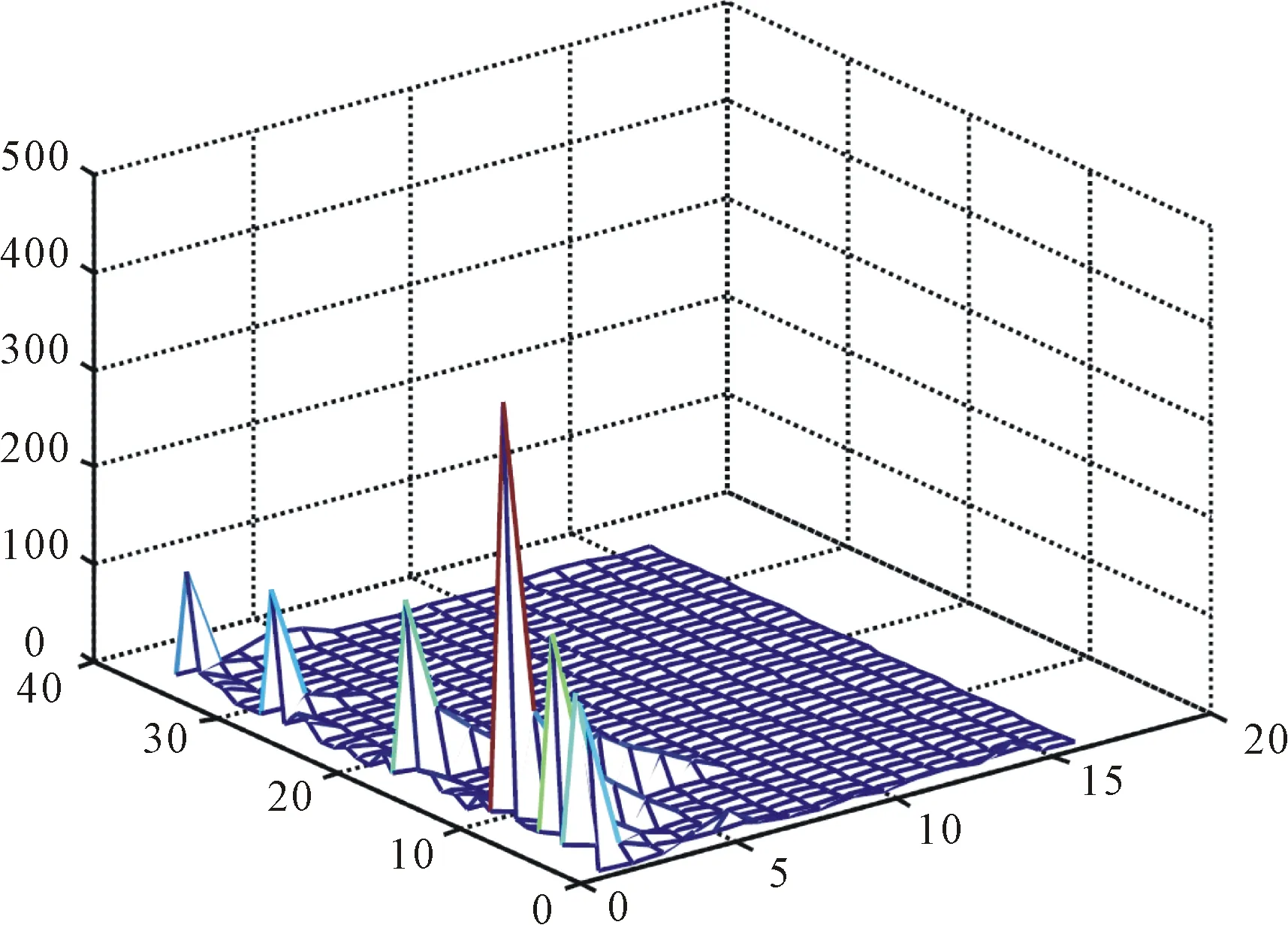
图3 IGBP与LC算子联合概率分布直方图

从图3可以看出，IGBP与LC算子联合可以把LC量化成16个区间，与IGBP构成一个大小为36×16的联合概率分布直方图。本文结合了图像纹理的强度与结构信息来对图像的纹理进行描述，在不同的纹理之间具备较强的可区分性。

2.1.2 图像颜色特征的提取

本文提取颜色特征作为描述目标区域的第二种特征。通常目标区域的颜色特征使用离散化的颜色直方图来表示，由于红、绿、兰(RGB)颜色空间容易受到光照变化的影响，故本文在HSV(H表示色度，S表示饱和度，V表示亮度)空间计算颜色直方图，并量化整个空间的间隔为m=16×16×16。第u个目标区域的颜色概率分布

(14)

其中，n表示目标区域像素点的个数。x表示目标区域的中心位置；xr(r=1,2,…,n)表示目标区域中像素的位置。h表示核带宽。函数b(xr)表示像素xr对应的直方图区间。δ定义为

(15)

k(x)为Epanechnikov核函数[11]

(16)

2.2 图像特征相似度的度量

在得到各个特征下候选模板与目标模板直方图后，计算Bhattacharyya距离[17]作为特征的相似性度量方法

(17)

其中，htar和hmod表示当前归一化后的候选模板和目标模板直方图；d越小，表示候选模板与目标模板之间的相似度越高，反之则相似度越低。

当在特定特征下获得候选模板与目标模板之间的Bhattacharyya距离时，特征观测概率值

(18)

其中，i=1,2，改进后的纹理特征属于提到的第一种特征，颜色特征则属于第二种特征。

2.3 图像特征的融合

在提取的纹理、颜色两种特征条件独立的情况下，采用文献[12]提出的多特征融合策略对这两种特征进行融合。具体做法为，在知道每个特征的观测概率值之后，添加与特征的不确定性成比例的均匀分布，再归一化，然后相乘以获得融合后的特征观测概率

(19)

其中，zi，i=1,2表示本文的2种特征；βi表示第i种特征所对应的不确定性，U(x)是一个离散的均匀分布，设粒子数为N，那么有U(x)=1/N。

2.4 模板的更新

传统的粒子滤波目标跟踪中，目标模板一直不变，这样在长时间跟踪过程中由于目标发生遮挡从而导致跟踪失败。本文通过在短时间内计算目标的变形程度来确定目标是否被遮挡，从而采用不同的更新策略对目标模板进行更新。

设第n帧与第n-Δn帧目标区域对应位置像素灰度值的平均绝对差之和

(20)

其中，m×n表示目标区域的大小，f(x,y)表示第n帧目标区域中(x,y)位置处的像素灰度值，t(x,y)表示第n-Δn帧目标区域中(x,y)位置处的像素灰度值。

按照以下更新策略对目标模板更新，新模板

p′=(1-η)ppre+ηpnew。

(21)

其中，ppre和pnew分别为前一帧的目标外观模板和当前帧的目标外观模板，η为学习速率。

设选取的阈值为T，若

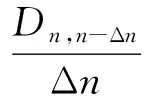
(22)

则判断目标发生遮挡，即停止模板更新。

Δn的选取也十分关键，不宜过大或过小。本文根据目标运动的速度对Δn进行自适应调整。目标速度可以根据其在视频流中的轨迹建立方程求得。确定了目标速度，如果目标被遮挡，变形的速度应近似等于目标运动的速度，因此Δn应近似等于目标运动的速度。

2.5 算法步骤

改进算法基于粒子滤波框架实现，具体步骤如下所述。

步骤1初始化。在视频第一帧中确定目标初始位置x1及目标区域大小。

步骤3预测。由xt=Axt-1+w，根据上一帧的状态xt-1得到当前帧的预测状态xt，A是状态转移系数，w是均值为0的高斯噪声。

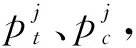
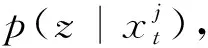
步骤6模板更新。首先按照2.4部分提出的遮挡判定方法判断目标是否发生遮挡，若是，则停止更新，否则以学习速率η为0.1对目标模板进行更新。

步骤7重采样。根据融合后粒子的权值分布进行重采样，并转到步骤3。

3 实验结果与分析

为了验证本文改进算法的性能，利用视频序列进行实验。算法在惠普Inter(R) Core(TM) i5-3450 CPU @3.10 GHz,4 GB内存的台式机上采用MATLAB R2014a编程实现。实验中，设定粒子数N=100，阈值T为26，学习率η为0.1。

3.1 定性分析

为了直观地说明本文改进后融合特征的效果，从TB100[18]中选取了3组具有代表性的视频序列Walking2、Basketball和Car1，在粒子滤波(PF)框架中将仅使用LBP特征、颜色特征和本文融合特征的跟踪效果进行对比，不同算法跟踪结果对比，如图4所示。其中，点线形矩形框表示仅使用LBP特征的跟踪结果，虚线形矩形框表示仅使用颜色特征的跟踪结果，实线形矩形框表示使用改进融合特征的跟踪结果。

在图4(a)中Walking2视频序列的前半部分，使用这3种特征的算法都可以有效跟踪目标，但是从第246帧开始，点线和虚线形矩形框开始偏离目标区域，到第281帧几乎完全偏离，此后完全跟丢。而使用改进后的融合特征则可以始终对目标进行有效跟踪。

在图4(b)中的篮球序列受到快速移动、相似颜色、严重形变等因素的影响。在视频序列的前半部分，3种特征均能对目标有效跟踪，如第2帧和第99帧所示，但从第280帧开始，点线形矩形框出现明显偏移，到第285帧完全偏离目标区域，之后，完全丢失，而改进融合算法始终能有效地跟踪目标。

在图4(c)中Car1序列的前半部分，所有特征都可以有效地跟踪目标，但在跟踪过程中，由第289帧可以看出，点线和虚线形矩形框明显偏离目标区域，在后续帧中完全跟丢。而改进后的融合特征算法始终可以有效跟踪目标。

图4 不同算法的跟踪结果对比

为了说明改进算法处理跟踪过程中遮挡问题的有效性，在TB100中选取Woman视频序列对改进算法进行验证，改进算法对Woman序列的跟踪结果,如图5所示。

图5 Woman序列的跟踪结果

由图5中可以看出，改进算法从目标发生遮挡到再次出现在视场中始终可以有效跟踪目标。

3.2 定量分析

为了定量分析改进算法的性能，引入中心位置误差、距离精度、重叠率和成功率[18]，以距离精度和成功率作为评价指标将本文算法与粒子滤波(particle filter, PF)[9]、颜色跟踪(color tracking, CT)[4]、核循环结构(circulant structure kernels, CSK)[5]、多目标跟踪(multi-task tracking, MTT)[6]等跟踪算法进行纵向对比。

从TB100中选取了11组具有代表性的视频序列，如表1所示，其中光照变化(illumination variation, IV)、面外旋转(out-of-plane rotation, OPR)、比例变化(scale variation, SV)、遮挡(occlusion, OCC)、变形(deformation, DEF)、运动模糊(motion blur, MB)、快速运动(fast motion, FM)、面内旋转(in-plane rotation, IPR)、超视距(out of view, OV)、背景噪声(background clutter, BC)、低分辨率(low resolution, LR)为视频序列属性，P表示该序列具有相应属性，“—”表示不具有相应属性。

表1 视频序列属性

用本文改进算法与PF、CT、CSK、MTT等跟踪算法进行纵向对比，对这11组视频序列进行实验，得到距离精度和成功率曲线，如图6和图7所示。

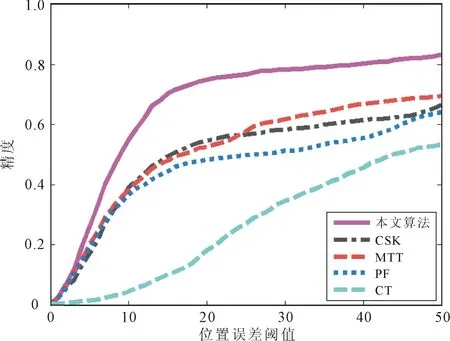
图6 距离精度曲线

图7 成功率曲线

当位置误差阈值为20个像素、重叠率阈值为0.5时，5种算法得到的距离精度和成功率，如表2所示。

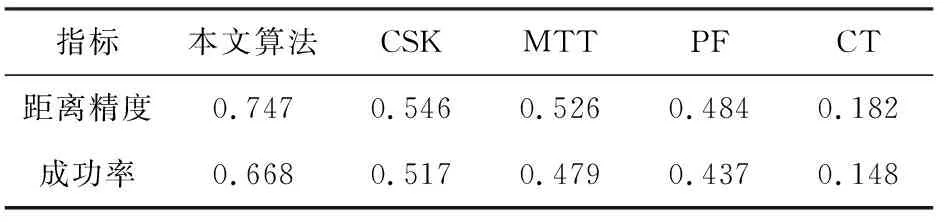
表2 距离精度和成功率

由图6、图7可以明显看出，本文算法得到的曲线优于其它对比算法。从表2可以看出，当位置误差阈值、重叠率阈值分别取为20个像素和0.5时，改进算法得到的距离精度为0.747，比CSK算法高出了0.201，成功率为0.668，也高出了0.151。通过定性和定量分析，不难发现，改进算法由于融合了不同的特征，使特征之间取长补短，有效地提高了复杂场景中单一特征跟踪效果差的问题，同时提出一种模板更新策略，可以对跟踪过程中出现的遮挡进行有效处理。

4 结语

针对于复杂的多目标场景，提出了一种基于改进纹理特征和颜色特征的多特征融合目标跟踪算法。通过计算特征的不确定性，在粒子滤波中实现这两种特征的自适应融合。通过判断目标是否发生遮挡，对于不同情况采用不同的模板更新策略跟踪目标。在TB100中选取不同的视频序列进行了实验，结果表明，本文的改进算法能够有效跟踪颜色相近、光照变化、遮挡等复杂场景中的目标。与PF、CT、CSK、MTT等跟踪算法进行对比，当位置误差阈值、重叠率阈值分别取为20个像素和0.5时，改进算法的精度和成功率均高于其他算法。因此，改进算法能够有效跟踪颜色相近、光照变化、遮挡等复杂场景中的目标。