基于改进的ICA和RBF神经网络的人脸识别
2018-12-26李乔深
吴 进, 李乔深, 赵 隽, 闵 育
(西安邮电大学 电子工程学院,陕西 西安 710121)
人脸识别是通过提取人脸视觉特征进行身份鉴别的一种计算机技术[1]。主要采用特征提取算法获取人脸图像的特征信息,将其送入分类器中进行分类识别,最后输出识别结果[2]。该技术已广泛应用在身份鉴别[3]、人机交互[4]、图像视频处理[5]等模式识别领域。
在人脸特征提取方面,常用的算法有主成分分析(principal component analysis,PCA)[6]和独立成分分析(independent component analysis,ICA)[7]。PCA在对样本进行特征提取的过程中,仅考虑样本的二阶统计信息,提取的特征并不能反映样本的高阶统计信息。利用ICA算法进行人脸特征提取时,也存在高维小样本的问题。针对这些不足,基于改进的PCA+ICA特征提取算法[8],通过PCA算法对图像进行去二阶相关和降维处理,不但可以消除噪声,而且还可以减少计算量,再通过ICA算法获取人脸图像独立基分量。基于局部人脸图像的ICA方法[9]是直接将人脸分成若干个相等的图像作为训练样本,进行ICA特征提取。此算法更能反映局部的特征信息,并且有效减少了对样本量的需求。然而,上述方法中ICA特征提取算法仍然存在运算复杂、收敛速度慢等问题,导致计算量大且耗时。
在选择分类器方面,常用的神经网络分类器有反馈(back propagation,BP)神经网络[10]和径向基函数(radial basis function,RBF)神经网络[11]。BP神经网络分类器在函数逼近时采用负梯度下降法调节权值,这种权值调节方法存在收敛速度慢和局部极小值的缺陷。RBF神经网络无论在逼近能力、分类能力和学习速度上都要优于BP神经网络。
为了提高人脸识别速度以及识别准确率,本文拟提出一种改进的ICA与RBF神经网络相结合的方法进行人脸识别。利用ICA算法对人脸图像进行特征提取,采用牛顿迭代法和加入松弛因子的方式,对ICA中的迭代算法进行改进,将得到人脸特征向量作为RBF神经网络的输入,利用监督聚类方法对神经网络进行构建和初始化,并采用线性最小二乘法对输出层连接权值进行调整,采用梯度下降法对隐含层中心以及高斯宽带进行调整,通过训练学习,输出分类识别结果。
1 ICA算法的改进
利用ICA进行人脸特征提取,人脸训练样本集X=[x1,x2,…,xn]可以表示为一组相互独立的基向量S和可逆混合阵A的线性组合
X=AS。
(1)
ICA算法的目的就是找到混合矩阵A的逆矩阵W,使其满足
I=WAS,
(2)
其中,I是独立基向量组S的估计,W=(w0,w1,…,wn)为权值变换矩阵,其中的元素即要提取的人脸特征。权值w的第k+1次迭代公式为
(3)
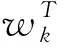
1.1 基于迭代性能的改进
利用雅可比矩阵[9]JF(w)对式(3)进行迭代计算。由于此迭代算法非常耗时,因此采用牛顿迭代法[12]将所有矩阵均取初始矩阵JF(w0)值,可将迭代公式(3)修正为
wk+1=wk-F(wk)/JF(w0)。
(4)
假定wk已求得,则
(5)
式(5)中,计算一次雅可比矩阵JF(w)的效果,相当于牛顿迭代法中计算m次迭代的效果。式(5)的收敛阶是m+1阶,当m取2时,其收敛速度相当于牛顿迭代算法的最快速度,而且少算一次雅可比矩阵。因此当m=2时,式(5)可简化为
(6)
1.2 基于初始权值依赖性的改进
为了有效的改善ICA算法对选取初始权值w0的依赖性,引入了松弛因子αk[13],将式(6)改写为
(7)
将式(7)两边同乘以β-E(g′(wTx)),得
(8)
选择松弛因子αk的标准是在某种范式下满足
(9)
因此,松弛因子的引入,保证了F(wk)在该范式下下降的特性。
2 RBF神经网络的改进
在完成特征提取之后,将人脸特征W=(w1,w2,…,wn)作为RBF网络的输入,进而对人脸特征模式进行分类识别。RBF算法是一种多变量插值算法。该网络由输入层、隐含层和输出层三层组成[14]。
对于基于特征的人脸图像的识别问题,RBF网络输入层的节点个数为提取到的图像特征向量的维数,输出层的节点个数即为待识别的人脸类别数。
算法具体描述如下。
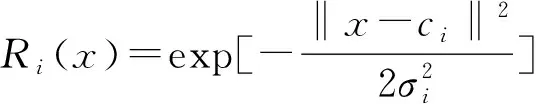
(10)
其中,Ri(x)代表RBF神经网络中隐含层第i个结点的输出;x代表n维的输入人脸特征向量;ci代表隐含层中第i个神经元节点径向基函数的中心位置;‖x-ci‖代表x-ci的范数;σi代表围绕径向基函数中心点的宽度;m代表神经元节点个数。在基函数的中心处,Ri(x)存在唯一的最大值,随着‖x-ci‖的增大,Ri(x)会迅速衰减为0。
2.1 RBF神经网络的构建和初始化
在构建和初始化RBF神经网络时,隐含层节点数量及其参数的选取特别重要,节点数量的多少会影响整个神经网络的复杂度[7]。本文使用一种监督聚类算法,来完成神经网络的设计。算法描述如下。
假设输入层的神经元数量为r,输出层的神经元数量为s。
步骤1初始化网络,RBF神经网络隐含层节点数量u,与输出层神经元数s相等,即u=s;
步骤2计算各个样本图像的均值,用作该类的初始中心。其计算公式为
(11)
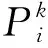
步骤3找出距离类k中心的最远点Pk(f),然后计算出该点到其类中心Ck的欧氏距离
dk=‖Pk(f)-Ck‖。
(12)
步骤4计算出类k的中心到类j的中心的欧式距离
dc(k,j)=‖Ck-Cj‖
(j=1,2,…,u;j≠k)。
(13)
找出式(11)计算结果中距离类k中心最小的距离和最近中心
dmin(k,j) = arg mindc(k,j)
(j=1,2,…,u;j≠k)。
(14)
根据dk、dl和dmin(k,l)之间的关系,对类k进行判断,有以下两种情况。
情况1若dk+dl≤dmin(k,l),则类k与别的类属于相离关系。
情况2若dk+dl>dmin(k,l),则类k与别的类有重叠的地方,此时分两种情况。
(1) 若dk+dl>dmin(k,l)且|dk-dl| (2) 若dk+dl>dmin(k,l)且|dk-dl|≥dmin(k,l)时,则类k与别的类属于包含关系。 步骤5分离原则。类k完全包含别的类,即dk+dl>dmin(k,l)且|dk-dl|≥dmin(k,l)或者类k包含别的类超过一个的特征,则该类k需要继续划分成两类,否则结束划分。 步骤6重复步骤2—步骤5,直至所有的类均无需划分为止。 RBF神经网络隐含层节点的中心宽度,影响着样本分类的最终结果[15]。为了避免中心宽度选择不当,导致出现无法区分样本的局面,需要通过控制隐含层节点的宽度来控制其在输入空间的覆盖范围。计算高斯宽度[16]表达式为 (15) (16) (17) dmin(k,l)为类k的均值到其他类的均值的最小间距,ξ为重叠因子,取值0.7≤ξ<1.8,调整RBF神经网络节点的重叠情况。ξ的取值可根据实验数据选取,也可根据下式计算得到 (18) RBF神经网络的参数调节过程,即为学习过程。采用梯度下降法对网络隐含层的中心和宽带进行调节;采用混合学习混合线性最小二乘算法,对输出层连接权值的大小进行调整[10]。 (1) 隐含层的中心和宽度调整 定义误差函数 (19) (20) 中心值C和宽度值σ的调整过程为分别使用误差率对中心值C和宽度值σ求偏导。 (21) (22) 式(21)和式(22)中,i=1,2,…,r,j=1,2,…,u,η代表学习速率。 (2) 对权值矩阵的调整 由节点生成算法知,r代表输入层神经元数量,s代表输出层神经元数量,u代表隐含层的节点数量。RBF神经网络的任何输入矩阵X∈r×N、输出矩阵Y∈s×N,权值矩阵W∈s×N和隐含层的输出矩阵R∈u×N存在 Y=W×R。 (23) 假设目标矩阵的期望输出为T∈s×N,为了达到实际输出与期望输出误差能量函数值 EET=(T-Y)T(T-Y) 最小的目的,选取线性最小乘法[13],通过R的伪逆矩阵R+求出最优的系数矩阵 W=T×R+, (24) 式中,R+=(RTR)-1RT,RT为R的转置矩阵。 将改进的两种算法相结合,进行人脸识别。基于改进的ICA和RBF人脸识别算法的识别过程如图1所示。 图1 RBF人脸图像的识别过程 具体实现步骤如下。 步骤1利用式(8)对ORL人脸样本进行特征提取。 步骤2将提取到的特征信息作为RBF神经网络的输入,并利用式(11)的监督聚类算法进行网络构建和参数初始化。 步骤3利用对神经网络高斯宽度进行估计。 步骤4利用式(19)和式(24)进行网络训练,完成后输出识别结果。 为了验证改进的人脸识别算法的有效性,将PCA+BP算法、PCA+RBF算法、ICA+BP算法、ICA+RBF算法与改进的ICA+RBF算法分别进行运行时间和识别准确率的对比实验。实验数据来自ORL[9]标准人脸库,此人脸库共由40个人,每人由10幅分辨率为112×92的图像组成。 将ORL人脸库中选取的所有图片作为识别数据,相同的6幅图像作为训练数据,分别对5种算法进行运行时间对比实验,结果如表1所示。 表1 5种算法的人脸识别速度对比 表1的结果表明,相同训练样本下,相比于其他人脸识别算法,改进算法在训练速度和识别速度上都是最快的,验证了改进算法的速度优势。 抽取相同的6幅图像作为训练样本,所有的人脸图像作为测试样本。识别率结果如图2所示。 图2 5种算法的人脸识别率对比 由图2可以看出,相同训练样本下,与PCA相比,ICA与两种神经网络相结合的识别率较高;与BP神经网络相比,RBF神经网络与两种特征提取方法相结合的识别率更高。并且,随着训练样本的增多,每种算法的识别率都明显提高,但改进算法识别率最高,在6个训练样本下达到97.9%。 改进的ICA和RBF神经网络人脸识别算法,基于ICA算法中的迭代公式,采用牛顿迭代法,引入松弛因子,提高了特征提取的效率。采用监督聚类法对RBF神经网络进行构建和初始化,使用线性最小二乘法,对输出层连接权值进行调节,使用梯度下降法对隐含层中心以及高斯宽度进行调节,提升了网络识别的准确率。对比实验结果表明,改进算法比PCA+BP算法、PCA+RBF算法、ICA+BP算法、ICA+RBF算法,在人脸识别上具有更快的识别速度和更高的识别率。2.2 RBF神经网络高斯宽度估计
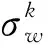
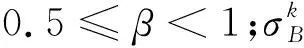
2.3 RBF神经网络的学习过程
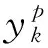
3 改进的ICA+RBF神经网络人脸识别
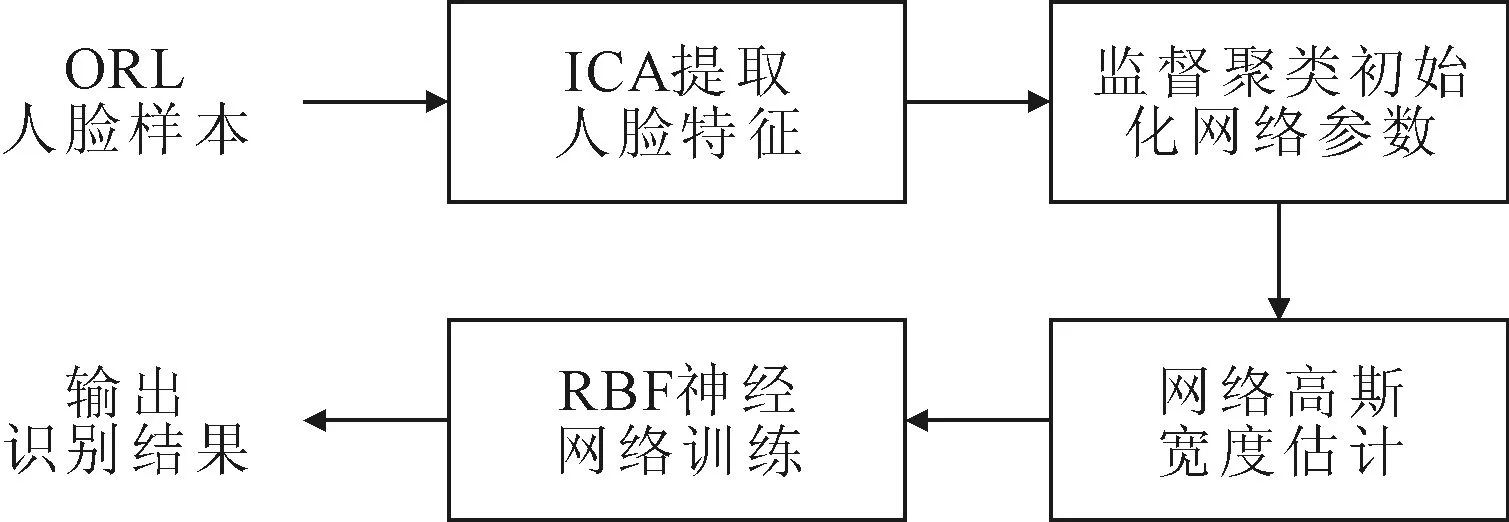
4 实验结果及分析
4.1 运行时间对比实验
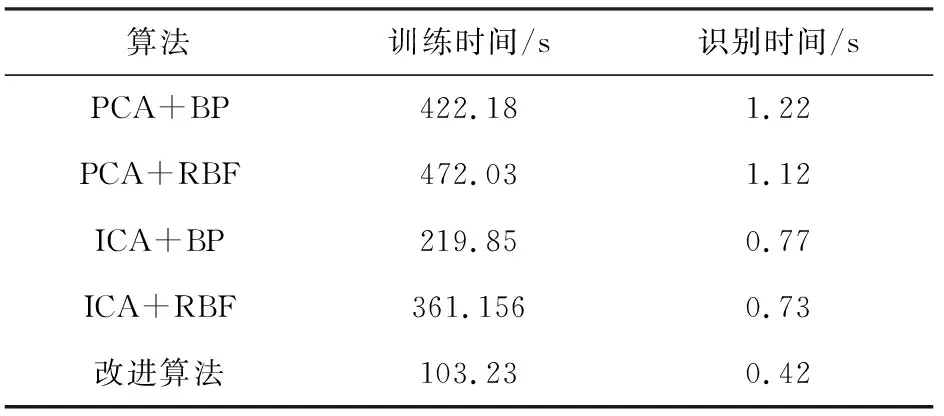
4.2 准确率对比实验
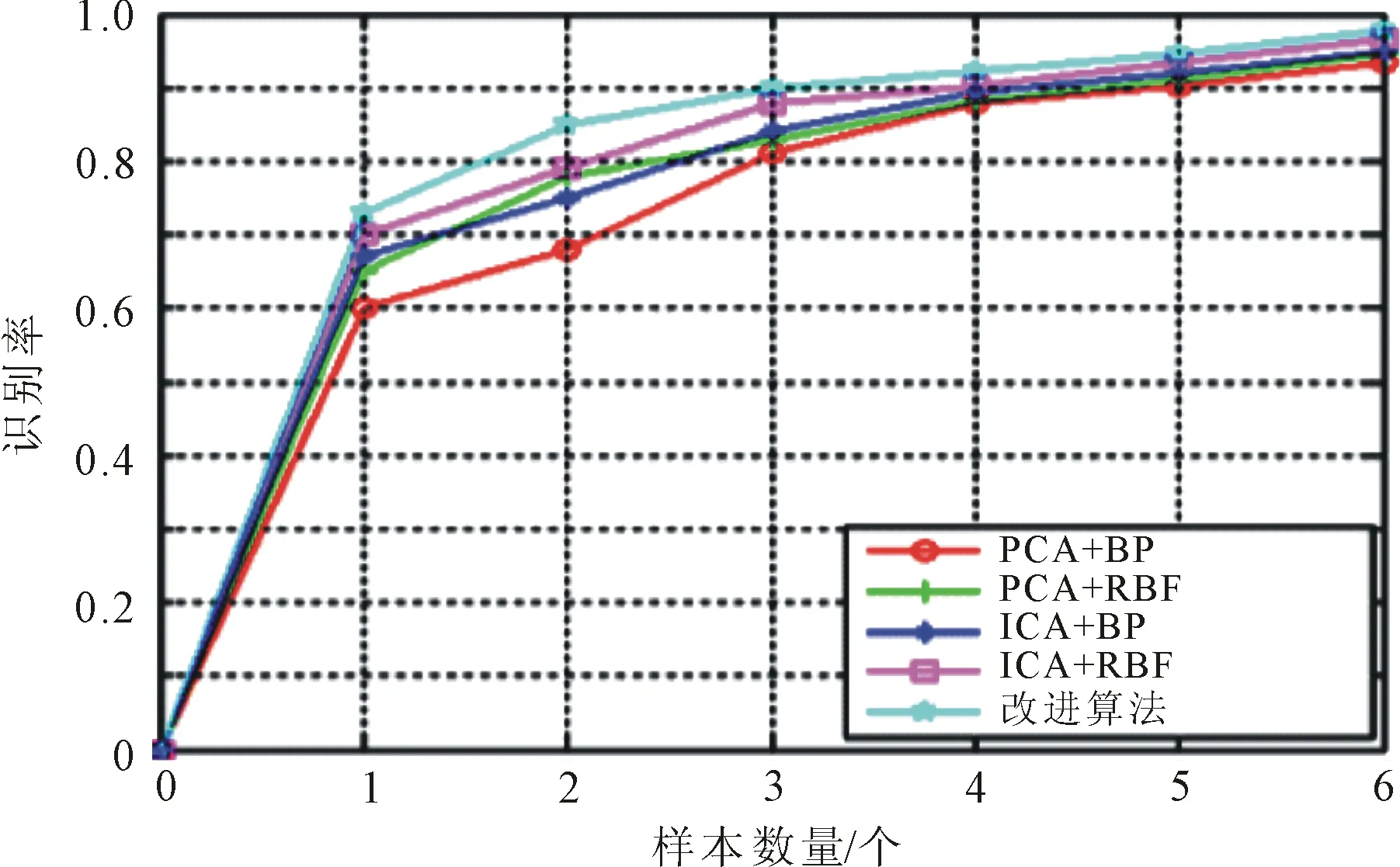
5 结语
