基于多目标区间值模糊聚类的含噪图像分割
2018-12-26李超琦
赵 凤, 李超琦
(1.电子信息现场勘验应用技术公安部重点实验室,陕西 西安 7101212.陕西省无线通信与信息处理技术国际合作研究中心,陕西 西安 7101213.西安邮电大学 通信与信息工程学院,陕西 西安 710121)
图像分割[1]是从图像处理到图像分析的关键步骤,现有的图像分割方法有基于阈值[2]、基于边缘[3]、基于区域[4]和基于聚类[5]等。基于聚类的分割方法中,模糊c-均值聚类(fuzzy c-mean clustering, FCM)算法[6]应用最为广泛。但是,在FCM算法中,模糊隶属度的设计包含各种不确定性(距离测度、模糊因子、原型等),为了减少模糊因子的不确定性对算法造成的影响,利用两个模糊因子构造区间二型模糊集,继而提出区间二型模糊c-均值聚类(interval type-2 fuzzy c-mean clustering, IT2FCM)算法[7]。针对原型的不确定性,将FCM算法进行改进,提出区间值数据模糊c-均值(interval value fuzzy c-mean clustering, IVFCM)算法[8]。
将区间值数据模糊算法应用到图像分割时,存在:(1)对图像噪声敏感。当图像被噪声污染时,没有考虑任何的空间信息,对噪声的鲁棒性差,分割结果不理想;(2)对聚类初始值敏感,容易陷入局部最优。为了解决上述问题,FCM_S1算法引入了局部均值的空间限制[9];基于非局部空间信息的模糊c-均值(fuzzy c-mean clustering algorithm with non-local spatial information, FCM-NLS)聚类算法将非局部空间信息引入到FCM算法,噪声的鲁棒性有所提高[10];基于粒子群优化的区间二型模糊(PSO-IT2FCM)聚类算法将粒子群优化算法引入IT2FCM算法[11]。但是,上述算法都只考虑单个目标函数,不能满足多方面的需求。多目标进化可变长遗传模糊聚类(multi-objective variable string length genetic fuzzy clustering, MOVGA)算法,采用类内紧致性和类间可分性作为适应度函数,可应用到医学大脑图像的分割[12]。
针对上述问题,本文提出一种多目标区间值模糊聚类(multi-objective interval valued fuzzy clustering, MIFCM)算法,将多目标优化引入到区间值模糊聚类算法中,利用迭代非局部均值(iterative non-local means, INLM)算法[13]对含噪图进行噪声点的去除,然后在其上构造一个对噪声鲁棒的区间值模糊图像,并且设计两个区间值模糊聚类有效性函数作为多目标优化的适应度函数,最后构造一个融合区间值模糊信息的最优解选解指标。
1 多目标区间值模糊聚类图像分割
1.1 对噪声鲁棒的区间值模糊图像的构造
INLM算法利用图像中大量的冗余信息即非局部空间信息平滑噪声。设图像X={x1,x2,…,xn},其中xi代表非噪声点的灰度值,则INLM的计算公式为
(1)
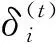
其中,h是平滑参数,σ代表高斯核的标准差,N(xi)表示以像素xi为中心,大小为s×s的邻域方阵中像素点的灰度值构成的向量,Zi是归一化常数,计算式为
当两次迭代之间的均方误差小于给定的阈值时,则停止迭代。最终得到处理之后的图像为R={δ1,δ2,…,δn}。
对于图像R,利用区间值模糊集[14]可表示为
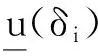
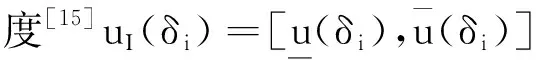
构造。然后利用m-模糊补算子[16]构造图像R中像素点δi的非隶属度
其中犹豫度π(δi)通过Yager算子[17]计算得出
π(δi)=1-u(δi)-v(δi),
所有的参数设置[14]分别为
g=150,σ=120,e=2,
w=0.2,α=0.1,β=0.1。
1.2 多目标区间值模糊聚类算法
1.2.1 染色体编码和种群初始化
染色体表示问题的潜在解。MIFCA算法利用实数可变长编码方式对聚类中心的区间隶属度和区间非隶属度进行编码。图1中展示了两类聚类问题的染色体编码。

图1 染色体编码方式
1.2.2 适应度函数
适应度函数用来描述种群中染色体的性能。MIFCA算法构造了两个融合区间值模糊信息的适应度函数,分别是全局区间模糊紧致性函数CIF和区间模糊可分性函数SIF。
为了计算这两个目标函数,提取编码在染色体上的聚类中心C={c1,c2,…,cK},计算隶属度
(2)
其中
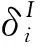
最后,全局区间模糊紧致性函数CIF和区间模糊可分性函数SIF分别定义为
(3)
(4)
1.2.3 选择、交叉和变异操作
选择过程是一种基于适应度的优胜劣汰的过程。MIFCA利用拥挤二进制锦标赛算[18]方法选择出父代染色体进行后续的交叉和变异操作。
由于是对聚类中心进行编码,因此在交叉时染色体上的聚类中心被认为是独立的,采用Laplace交叉算子[19]对父代染色体进行操作产生子代染色体。
为了扩大种群的多样性,使算法拥有全局搜索能力,变异操作是必不可少的一个环节。将区间值模糊信息引入Poisson变异算子[20],构造区间模糊Poisson变异算子,从而对染色体上的基因位进行修改,具体操作如下。
产生一个[0,1]之间的Poisson分布随机数ξ,如果选择聚类中心ck的第d维数据ckd进行变异,则变异之后ckd的隶属度为
变异之后ckd的非隶属度为
1.2.4 精英策略和最优解的选择
NSGA-Π最有特色的部分就是它的精英策略,父代和子代的非支配解都会遗传到下一代,这就确保了目前找到的最优解不会丢失。
在算法的最后一代会产生一个非支配解集,解集中的每一个解都是同等重要的,但是在实际生活中,用户只需要一个解,所以,从中选择出一个合适的解是很必要的。MIFCA算法采用一个新的选解指标——最优解区间值模糊聚类指标[21]
(5)
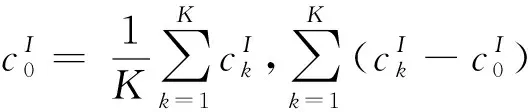
MIFCA算法具体步骤如下。
步骤1输入图像,最大迭代次数G,种群大小P,交叉概率Pc,变异概率Pm和最大类别数Kmax。
步骤2利用INLM算法对输入图像进行噪声的去除并在其上构造区间值模糊图像。
步骤3初始化种群,设置迭代次数g=1,根据式(3)和式(4)计算初始种群中每条染色体的两个适应度函数:全局区间模糊紧致性函数CIF和区间模糊可分性函数SIF。
步骤4对种群中的个体执行非支配排序。
步骤5采用拥挤二进制锦标赛方法产生交配池。
步骤6在交配池中,对父代种群进行Laplace交叉和区间模糊Poisson变异,产生子代种群。
步骤7根据式(3)和式(4)计算子代种群中每个个体的两个适应度函数:全局区间模糊紧致性函数CIF和区间模糊可分性函数SIF。
步骤8对父代种群和子代种群进行精英策略产生下一代种群,并令迭代次数g=g+1。
步骤9判断终止条件,若达到最大迭代次数,则利用式(5)从最后一代非支配解集中选择一个最优的染色体,对该染色体进行解码得到最终的聚类中心,再利用式(2)计算隶属度矩阵,根据最大隶属度原则对像素点进行聚类,从而得到图像的分割结果。否则,返回到步骤4。
2 实验及结果分析
采用1幅人工合成图、6幅Berkeley图像[22]和2幅刑侦图像[23]进行图像分割实验,并对这9幅图像分别添加高斯噪声和椒盐噪声。为了更好地验证MIFCA算法的有效性,将FCM、FCM_S1、IT2FCM、IFCM[24]、IVFCM、MOVGA和MSFCA算法与MIFCA算法进行比较,并利用准确率[25]来评价各算法的性能。
对于各算法涉及到的参数作如下说明:FCM、FCM_S1、IT2FCM、IFCM和IVFCM算法的最大迭代次数为100,终止阈值设置为10-5[26];FCM_S1和MSFCA算法的权值取λ=6[27];MOVA,MSFCA和MIFCA的迭代次数G=100,种群规模P=50,交叉概率Pc=0.9和变异概率Pm=0.1[27]。对于MSFCA和MIFCA,非局部空间信息中搜索窗大小r×r为21×21,相似窗大小s×s为7×7,平滑参数h为30[13]。
2.1 人工合成图像实验结果
人工合成图的分割结果分别如图2和图3所示,分割准确率的统计结果如表1所示,其中图2是添加均值为0,方差为0.01的高斯噪声图分割结果,由于MSFCA和MIFCA算法引入了非局部空间信息,所以可以滤除掉大部分噪声点,而其他对比算法对噪声的鲁棒性较低。图3是强度为0.1的椒盐噪声图的分割结果,可以看出,MIFCA算法对椒盐噪声的鲁棒性也较高。表1中的准确率数据也说明了MIFCA算法对噪声的鲁棒性较高,分割效果较好。

图2 人工合成图高斯含噪图像分割结果

图3 人工合成图椒盐含噪图像分割结果

表1 人工分割图准确率对比
2.2 自然图像实验结果
8种方法在6幅Berkeley含噪图像上的分割准确率如表2所示,由于MIFCA算法引入了非局部空间信息,并且预先构造了对噪声鲁棒的区间值模糊图像,所以MIFCA在所有图像上都获得了最高的准确率。为了展示视觉分割结果,选取图像#3096和#15088在不同噪声水平下的含噪图像分割结果进行展示。图像#3096添加均值为0,方差为0.01的高斯噪声的分割结果如图4所示,添加强度为0.2的椒盐噪声的分割结果如图5所示,从两幅图中可以看出,MIFCA算法可以正确地将飞机从整幅图中完整地分割出来,并且左下角容易错分的区域也可以正确处理。图像#15088分别添加了均值为0,方差为0.025的高斯噪声和强度为0.1的椒盐噪声。图6和图7中展示了8种方法的分割结果,可以看出,MIFCA算法对高斯噪声和椒盐噪声都有一定的鲁棒性,可以较好地将船与背景分割出来。
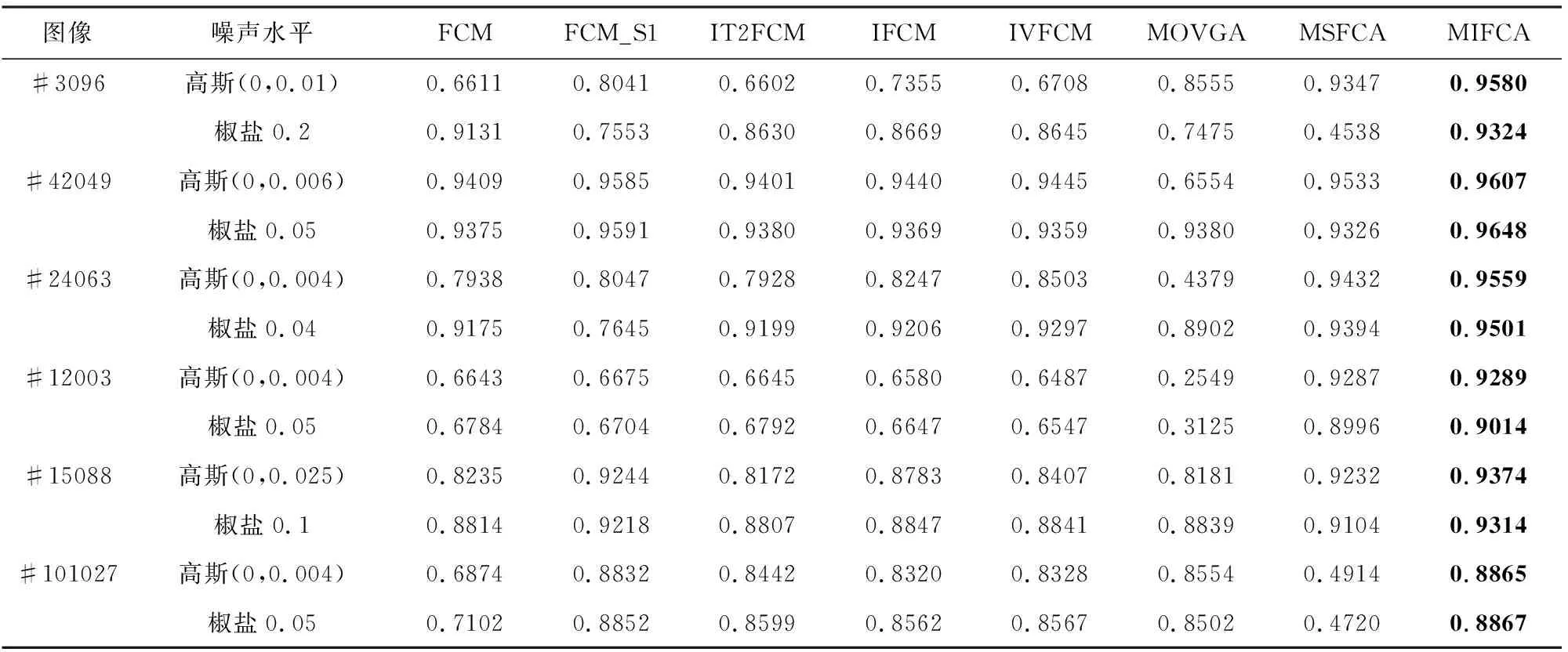
表2 8种算法分割准确率对比

图4 #3096高斯含噪图像分割结果

图5 #3096椒盐含噪图像分割结果
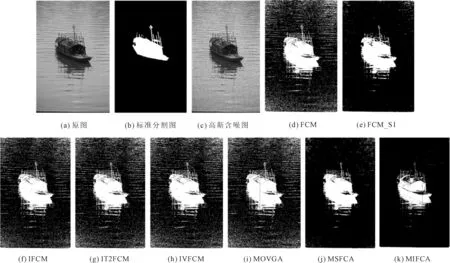
图6 #15088高斯含噪图像分割结果
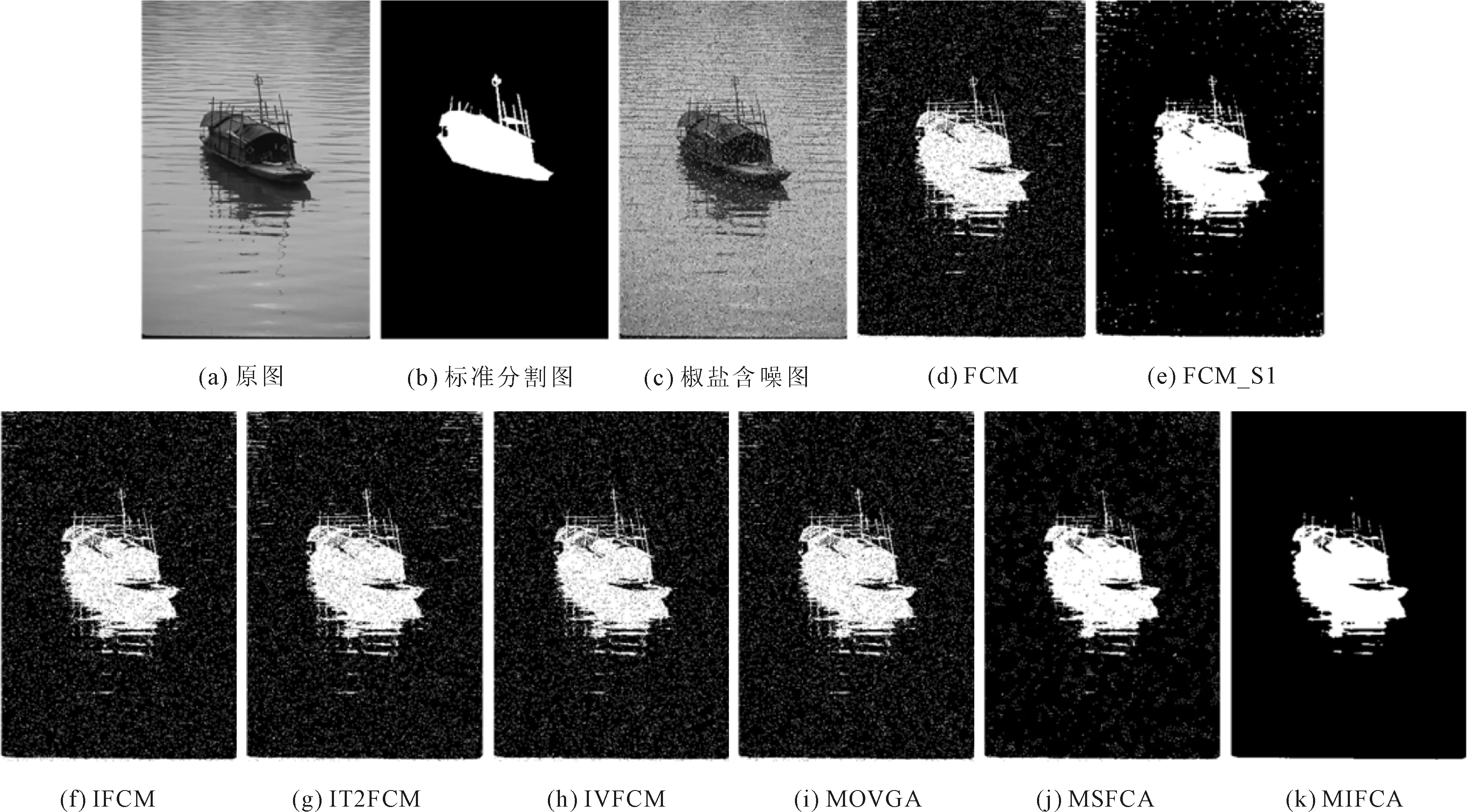
图7 #15088椒盐含噪图像分割结果
2.3 刑侦图像实验结果
为了验证MIFCA算法对刑侦图像的分割效果,选择刀具和鞋印两幅刑侦图像,对其分别添加均值为0,方差为0.006的高斯噪声和强度为0.04的椒盐噪声。
刀具的分割结果分别如图8和图9所示。可以看出,MIFCA算法引入了非局部空间信息并且构造了一个对噪声鲁棒的区间值模糊图像,可以去除大部分的噪声点,更好地保留了刀具上的细节部分和边缘部分。鞋印的分割结果分别如图10和图11所示,可以看出,MIFCA算法对噪声鲁棒性较高,并且对鞋印中细纹的细节保护的较好。

图8 刀具高斯含噪图像分割结果

图9 刀具椒盐含噪图像分割结果
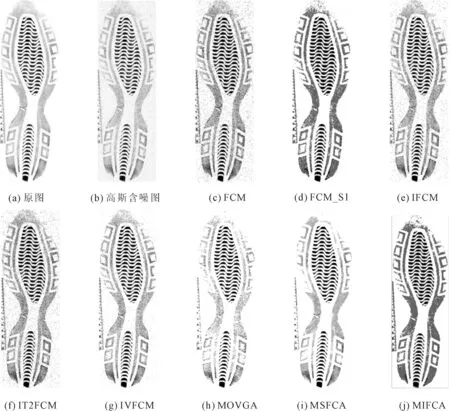
图10 鞋印高斯含噪图像分割结果
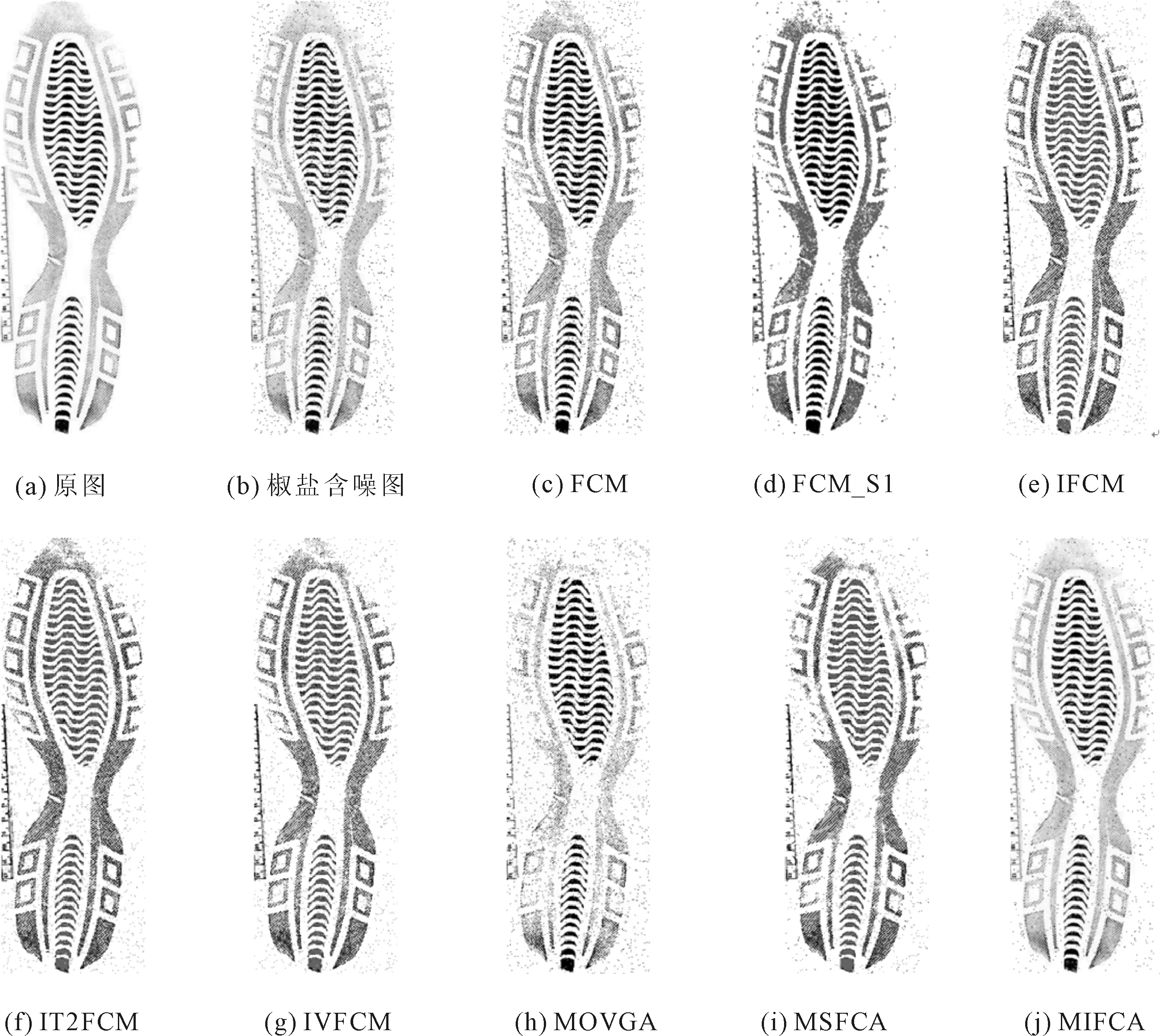
图11 鞋印椒盐含噪图像分割结果
3 结语
MIFCA算法将多目标进化引入到区间值模糊聚类算法中,构造出两个区间值模糊聚类适应度函数以及选解指标,解决了区间值模糊聚类算法对噪声敏感、容易陷入局部最优以及单目标优化的缺点。仿真实验结果表明,该MIFCA算法能够较好地分割含噪图像,具有更优的分割性能。
