基于EEMD与Elman网络的 灌区地下水埋深预测模型
2018-12-26张先起胡登奎
张先起,宋 超,胡登奎
(1.华北水利水电大学水利学院,郑州 450046;2. 水资源高效利用与保障工程河南省协同创新中心,郑州 450046)
0 引 言
灌区地下水埋深变化是一个复杂的、模糊的和不确定性的系统,影响地下水埋深变化的因素有很多,地下水开采、土壤地质条件、地表蒸发与植物蒸腾[1]等都会引起其变化。准确的预测地下水埋深变化可为灌区地下水保护、种植结构与模式调整、水土资源的合理利用与生态环境保护等提供理论依据。国内外关于地下水埋深预测模型的研究比较重视,且已取得了较丰硕的成果。Zhang等[2]运用GSM、RBF和ANFIS模型对吉林市的非承压含水层地下水埋深进行了预测;Adhikary等[3]采用交叉验证方法比较IDW、RBF、OK、UK插值方法在地下水位预测中的效果;Al-Mahallawi等[4]利用神经网络预测农村农业地区的地下水硝酸盐污染的变化;Maiti等[5]运用三种神经网络模型对地下水位进行预测;杨忠平[6]等运用时间序列模型预测吉林省地下水的动态变化;沈冰等[7]利用灰色记忆模型对新疆和田地下水埋深进行了预测;李荣峰等[8]采用自记忆模型对山西晋中地下水埋深进行了预测。由上可知,国内外研究人员对地下水埋深预测模型的研究主要集中在对地下水埋深时间序列回归分析与利用模糊理论、灰色理论与神经网络等方面。影响灌区地下水埋深变化的因素有很多,且具有随机性、不确定性与模糊性等。Elman神经网络具有较强的自主学习适应能力及泛化能力,在非线性时间序列预测中被广泛应用[9]。集合经验模态分解法[10](Ensemble Empirical Mode Decomposition,简称EEMD)是从原信号中提取固有模态函数(IMF),从而分离信号的低频与高频部分,来实现对非平稳化序列的平稳化处理。虽然EMD分解和神经网络在地下水埋深中均有应用[11-13],但是利用EEMD和Elman网络结合起来构建灌区地下水埋深预测耦合模型较为少见。论文结合EEMD和Elman神经网络的优势,建立了基于EEMD和Elman网络的地下水埋深预测耦合模型,并将其应用于人民胜利渠灌区的地下水埋深预测中。
1 基本原理与方法
1.1 EEMD
经验模态分解[14](Empirical Mode Decomposition,简称EMD)是依据数据自身的时间尺度特征来进行信号分解,且无须预先设定任何基函数,该方法在处理非平稳及非线性数据上,具有非常明显的优势。集合经验模态分解是经验模态分解的改进算法,相比于EMD,EEMD在信号中加入了高斯白噪声,以其均匀分布的特性补偿IMF分量丢失的尺度[15],从而改变极值点的特性,使信号在不同尺度上具有连续性,有效避免了EMD的混频现象。EEMD最大特点在于其能够以自适应方式提取信号的各分量及变化趋势[16],从而降低序列的非平稳性,将非平稳的时间序列转化为平稳且相互影响甚微的序列。
地下水埋深受多种影响因素的影响,其变化具有随机性、不确定性与波动性。研究选取EEMD就在于它可以将信号的波动性、趋势性提取出来,将非平稳的时间序列转化为平稳且相互影响甚微的序列,进而可以将复杂的地下水埋深演变转化成对多个简单的单一变量的预测相加,以达到减小预测误差的目的。
EEMD分解的实现步骤如下所示:
(1) 在原始的地下水埋深序列(f(t))中添加一个随机白噪声序列(ξ(t)),从而得到一整体序列F(t)。
F(t)=f(t)+ξ(t)
(1)
(2)对F(t)进行EMD分解,得到IMF分量和趋势项。
(2)
(3)每次加入方均根相等的不同白噪声序列,重复步骤(1)、(2),得到k组不同的IMF分量和剩余分量。
(4)将相应的IMF取均值作为最终IMF组。
(3)
式中:k为添加白噪声序列的数目。
1.2 Elman 神经网络
Elman神经网络由Jeffrey L. Elman[17]于1990年提出,Elman是一种反馈式神经网络,该网络由4层组成,分别是输入层、隐含层、承接层、以及输出层组成。Elman神经网络相对于BP网络,是在BP网络的隐含层中多增加了一个承接层,作为延时算子来实现对系统的记忆,从而使系统具有适应时变特性的能力,由于Elman网络具有良好的记忆功能和稳定性特点,该网络在时间序列的预测效果上要优于BP网络,因此,Elman网络被广泛的应用于各个领域[18,19]。Elman网络结构如图1所示。
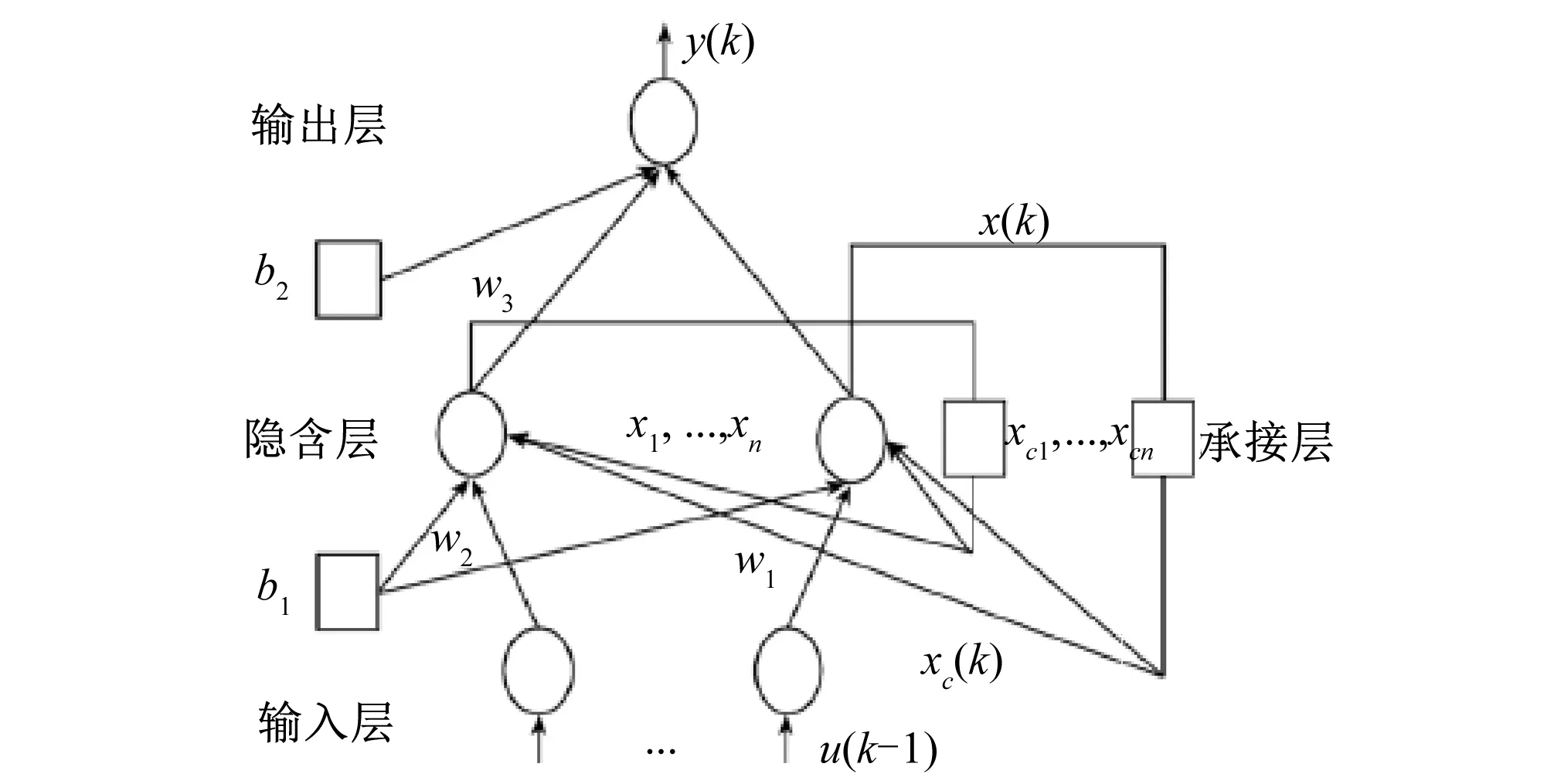
图1 Elman网络结构Fig.1 Elman network structure
图1中输入向量u为r维向量,输出向量y为n维向量,xc为n维反馈状态向量,w3为隐含层到输出层的连接权值,w2为输入层到隐含层的连接权值,w1为隐含层到承接层的连接权值,Elman网络模型的表达式如下,
y(k)=g(w2x(k))
(4)
x(k)=f(w2xc(k)+w2(u(k-1)))
(5)
xc(k)=x(k-1)+axc(k-1)
(6)
式中:g()为输出神经元的激活函数,为隐含层输出的线性组合;f()为隐含层神经元的激活函数,常采用S函数;a为自连接反馈增益因子,0≤a≤1。a=0时,网络为标准的Elman网络,a≠1,网络为修改的Elman网络。
Elman网络采用BP算法进行权值修正,学习指标函数采用误差平方和函数,表达式为:
(7)

2 基于EEMD和Elman网络的耦合模型
从EEMD分解角度来说,各IMF分量和残差对地下水埋深序列的贡献率不尽相同,可近似将IMF分量和残差看作地下水埋深的驱动因素。则地下水埋深预测就相当于IMF分量和残差的预测。
EEMD-Elman耦合模型具体步骤如下:
(1)利用MATLAB对1993-2013年的人民胜利渠灌区月地下水埋深序列进行EEMD分解,得到地下水埋深序列的IMF分量和残差。
(2)对地下水埋深序列的IMF分量和残差进行标准化处理。
如果网络的输入或输出数据的范围相差较大,网络的预测模型将会存在较大误差,因此我们必须对数据进行标准化处理,使数据范围在[0,1]内。
(3)将1993-2011年的地下水埋深的IMF分量和残差作为Elman网络的训练数据,2012-2013年的IMF分量和残差作为Elman网络的预测数据。
(4)利用Elman网络对2012-2013年地下水埋深的IMF分量和残差进行预测。
(5)最后将预测的地下水埋深IMF分量和残差依据公式(2)进行累加还原,并与原始的地下水埋深数据比较。
3 实例应用
3.1 区域概况
人民胜利渠灌区地处河南省北部,是我国建国以来在黄河下游兴建的首个引用黄河水灌溉的大型自流灌区。灌区属暖温带大陆性季风型气候,年平均气温14 ℃,无霜期220 d,年平均水面蒸发量1 300 mm,年平均降水量620 mm,灌区内总土地面积为1 486.84 km2。本文数据来源于1993-2013年灌区观测井的监测数据。
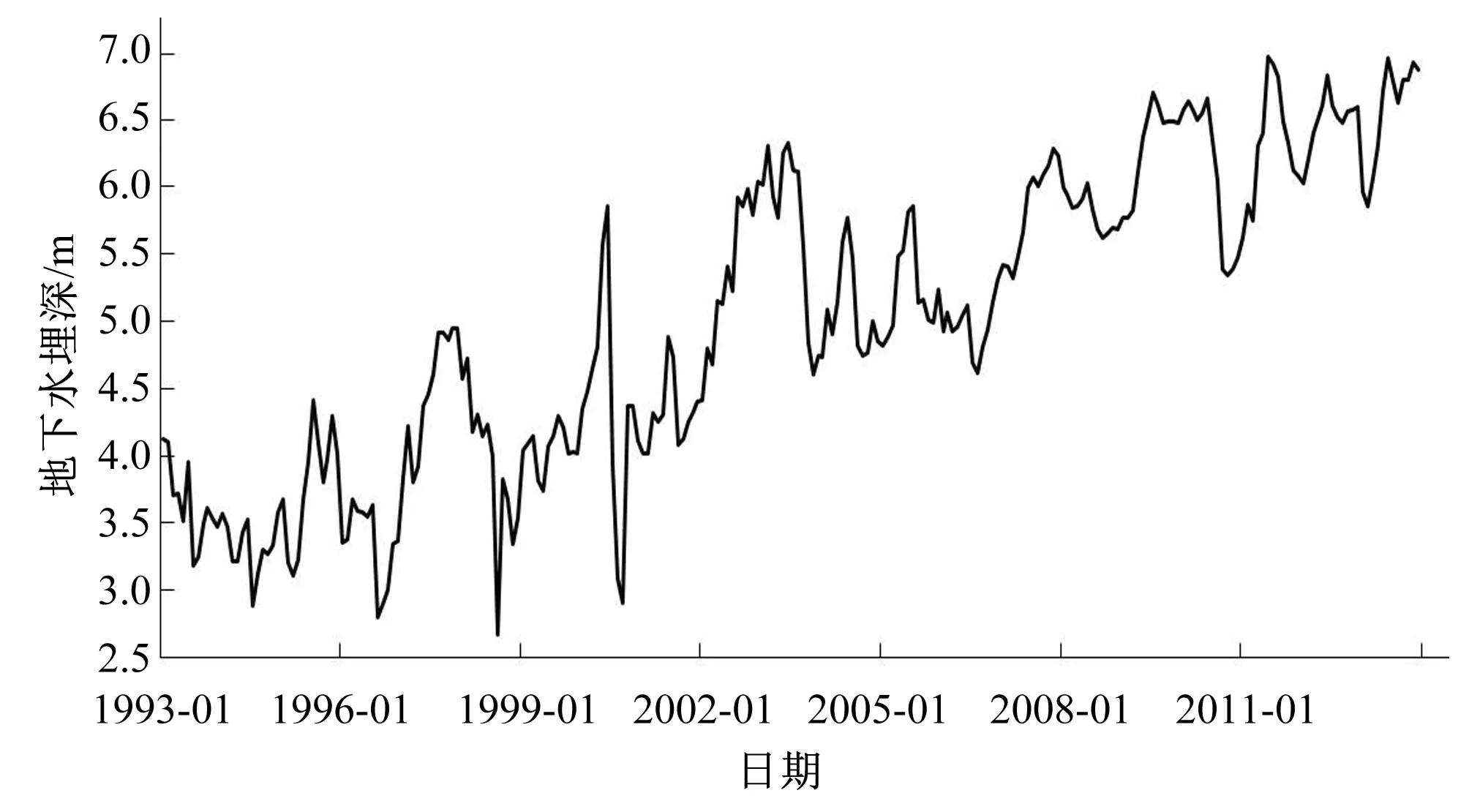
图2 人民胜利渠灌区1993-2013年地下水埋深曲线Fig.2 Groundwater depth curve of the people's victory canal irrigation district from 1993-2013
从图2中可以看出,1993-2013年间,人民胜利渠灌区的地下水埋深大致呈现出上升的趋势,上升过程中伴随着一定的波动性,且波动幅度不一致,这也验证了地下水埋深具有不确定性、非平稳性,这也从侧面反映选用EEMD方法是合理的。
3.2 EEMD分解
按照前面EEMD分解的步骤,对人民胜利渠灌区1993-2013年的地下水埋深数据进行EEMD分解,噪声方差取0.2,噪声次数取100。分解结果如图3所示。

图3 人民胜利渠灌区1993-2013年地下水埋深EEMD分解Fig.3 EEMD decomposition of groundwater depth in the people's victory canal irrigation district from 1993-2013
从图3可以看出,地下水埋深序列被分解为6个IMF分量和一个对应的残差。其中,第一个IMF分量波动性最大,频率高、波长最短;其他IMF分量振幅逐渐减小,频率逐渐降低,波长逐渐变大。人民胜利渠灌区地下水埋深序列经过EEMD处理后,序列的波动性、非平稳性大大降低。
3.3 地下水埋深预测
在利用Elman网络对人民胜利渠灌区地下水埋深进行预测时,必须进行训练、测试样本的划分。将1993-2011年的IMF和残差数据作为训练样本,2012-2013年的IMF和残差数据作为测试样本。采用滚动预测的方式,用连续19年第i个月的数据预测第20年的第i个月的数据。
通过大量反复试验,得出网络模型最优对应的隐含层节点数为10,隐藏层神经元传递函数为tansig,输出层神经元传递函数为purelin,网络训练函数定为traingdx,训练次数为1 000次,训练目标误差为10-4。
依据前面的步骤,利用Elman网络对人民胜利渠灌区2012-2013年地下水埋深的6个IMF分量和一个残差进行预测,预测结果如图4所示。
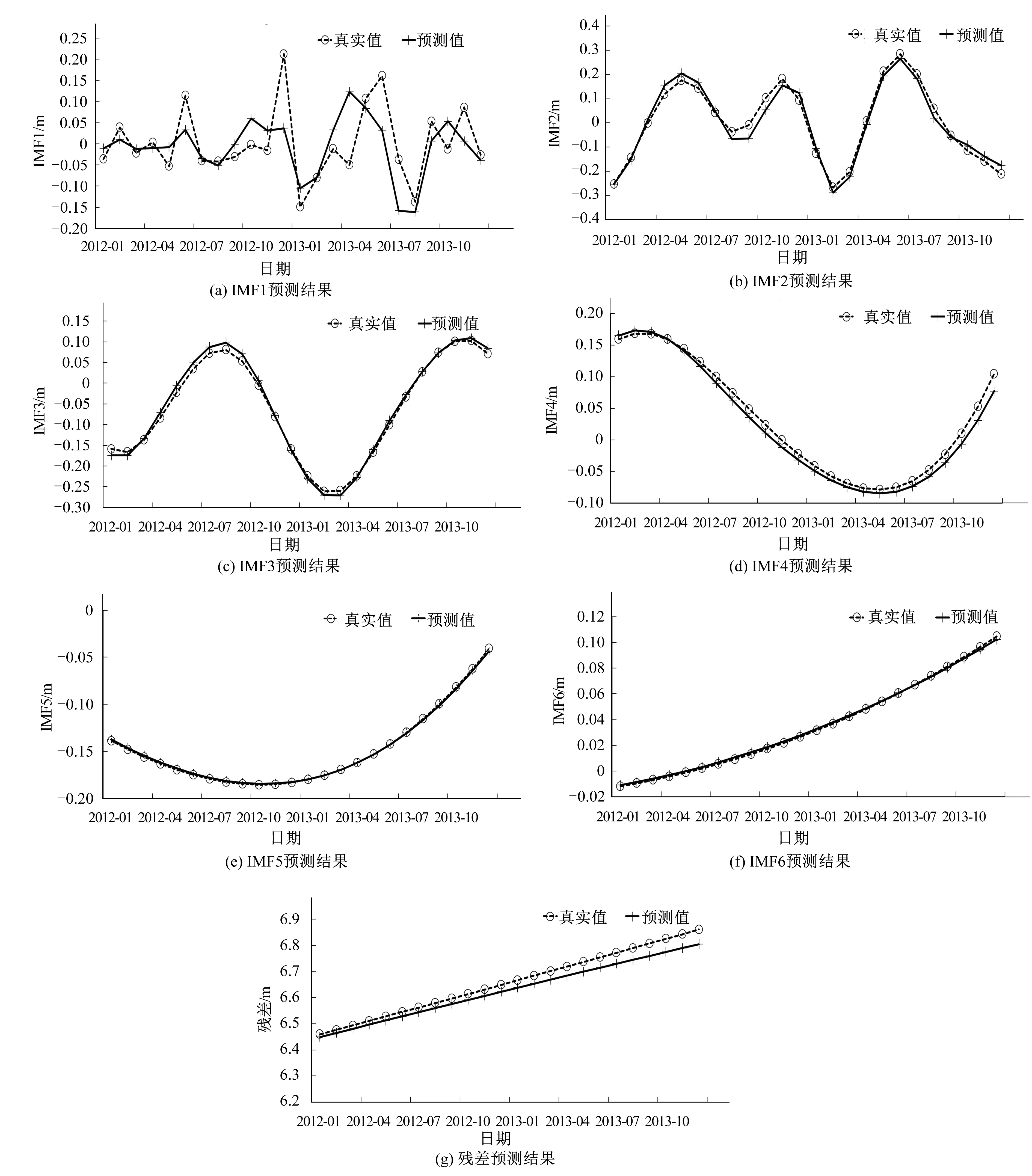
图4 IMF1~IMF6、残差预测结果Fig.4 The prediction results of IMF1~IMF6 and Residual
由图4可以看出,IMF1分量的预测效果略差,这说明IMF1分量非平稳性要高一些;IMF2~IMF6的预测效果较好,这说明IMF2~IMF6分量非平稳性要低一些,地下水埋深序列经过EEMD分解后,序列的波动性、非平稳性大大降低。

表1 IMF1~残差的相对误差指标 %
由表1可以看出,IMF1相对误差的最大值、最小值、平均值均较大,分别为2 714.10、0.81、245.83,这说明IMF1分量非平稳性要高一些,对预测误差影响较大;残差相对误差的最大值、最小值、平均值均较小小,分别为0.82、0.16、0.44,这说明低频信号相对平稳,对预测误差影响较小。由表1可以看出,地下水埋深序列经过EEMD分解后,IMF分量愈趋于平稳,IMF1残差的相对误差的各项指标整体呈现出逐渐减小的趋势。
由表2可以看出,EEMD-Elman耦合预测模型相对误差的最大值、最小值、平均值分别为2.91%、0.04%、1.09%,模型预测相对误差较小,合格率较高。
图5是人民胜利渠灌区2012-2013年地下水埋深的预测曲线,由图5可看出,人民胜利渠灌区2012-2013年地下水埋深的预测值与真实值基本一致,EEMD-Elman耦合模型的拟合度较高。
3.4 讨 论
表3为EEMD-Elman模型与其他模型的预测误差对比结果。
从表3可以看出,EEMD-Elman耦合模型对地下水埋深预测的合格率为100%,且相对误差较低,模型要明显优于单一的Elman网络模型和BP模型,模型较好的克服了Elman网络和BP网络对一些高频数据不能很好的学习的缺点,从而使预测精度提高。

图5 人民胜利渠灌区2012-2013年地下水埋深预测曲线Fig. 5 The groundwater depth prediction curve of people’s victory canal irrigation district from 2012-2013
4 结 论
(1)地下水埋深序列经过EEMD分解,其随机性、波动性降低,这为耦合模型预测提供了良好的条件。EEMD-Elman耦合模型预测相对误差小于2.91%,模型合格率为100%,精度较高,并优于单一Elman和BP神经网络。这表明EEMD-Elman耦合模型用于灌区地下水埋深预测是可行的。
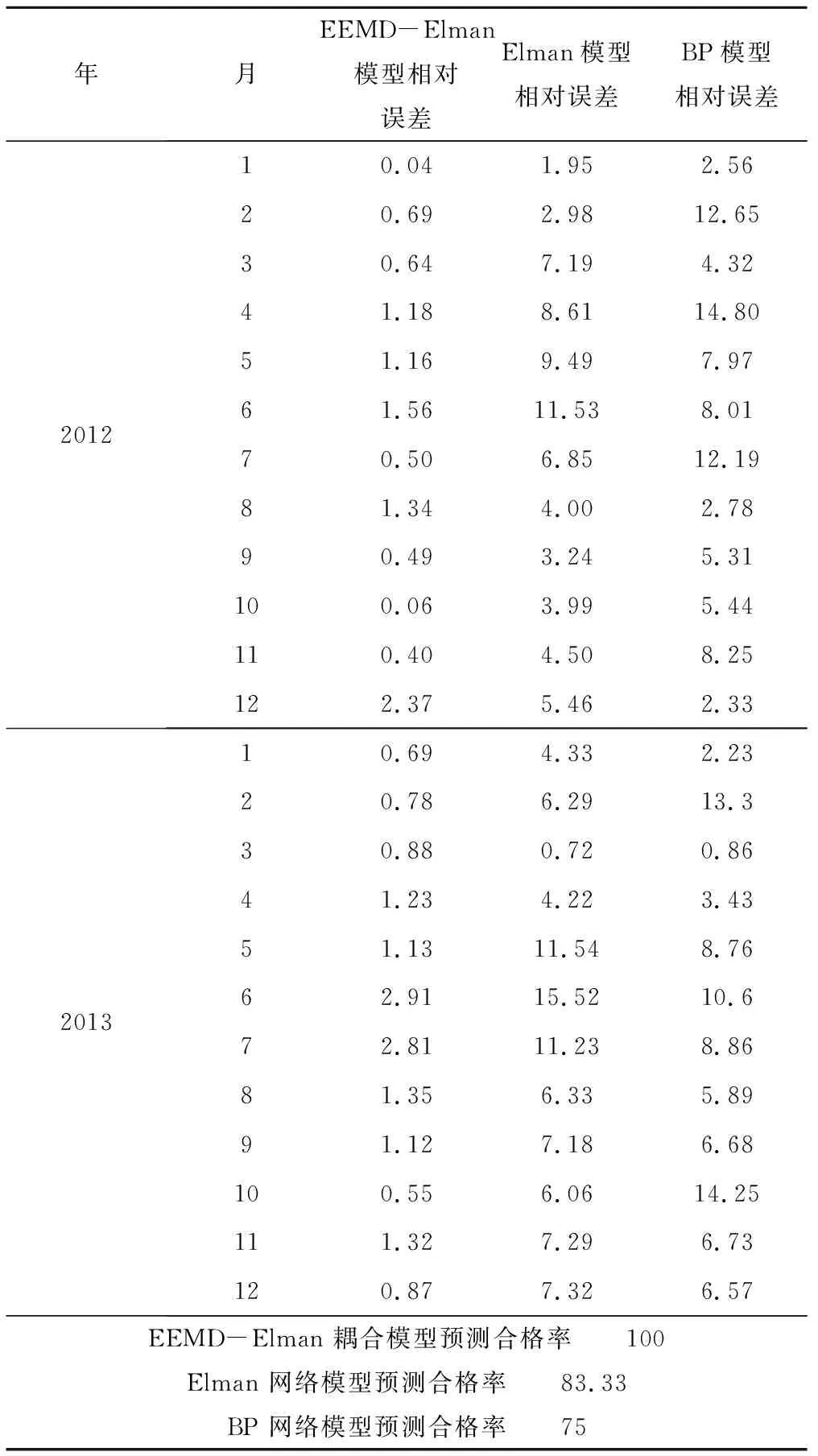
表3 EEMD-Elman模型与其他模型的对比 %
(2)在地下水埋深序列进行EEMD分解的基础上,利用Elman 网络对IMF1~残差进行预测,解决了直接用Elman网络对一些高频突变数据不能很好的学习问题。通过对EEMD分解后的各成分进行预测—重构,能够较好的拟合真实值。相比于传统的Elman网络和BP网络,模型在细节上能合理的反映序列的真实变化。
(3)地下水埋深时间序列经过EEMD分解,信号被分解为若干个IMF分量和残差,其预测值等于若干个IMF分量和残差的预测值相加。尽管有些IMF分量预测误差相对偏大,但这部分IMF分量在整个信号中所占成分较少,将IMF分量和残差的预测值转换成整体预测值时,整体误差将会减弱。
(4)尽管建立的EEMD-Elman耦合模型预测精度较高,但也有不足之处,比如网络参数需要人为设定和调整,研究仅仅对地下水埋深做了短期预测,没有进行长期预测,预测模型没有考虑地下水埋深变化的物理机制,这些都是需进一步研究的方向和重点。
