微咸水矿化度与滴头流量 对土壤湿润体的影响与模拟
2018-12-26王泽鹏郭向红
王泽鹏,郭向红
(1.山西省西山提黄灌溉工程建设管理中心,太原 030024;2.太原理工大学 水利科学与工程学院,太原 030024)
干旱和水资源短缺是制约我国北方地区农业可持续生产的主要因素。解决这一问题的主要方法有两类,一是开源,二是节流。在我国北方平原地区储存着大量的微咸水,大量研究表明这些低矿化度的微咸水可以用于灌溉,提高作物产量,因此微咸水合理利用是开源的主要途径之一[1]。同时,滴灌是目前应用广泛的节水灌溉方法,在我国得到了大面积推广。因此,将微咸水应用于滴灌,充分发挥滴灌和微咸水的优点,对微咸水合理高效利用就尤为重要。大量研究表明,滴灌的土壤水分主要分布在以滴头为中心的椭圆形湿润体内,并且使土壤中的盐分在水分的淋洗作用下,运移聚集在湿润体的边缘,造成湿润体内盐分较小,从而有利于作物生长[2,3]。因此,滴灌土壤湿润体的大小对作物生长十分重要。目前许多学者对滴灌湿润体进行了大量研究,主要集中在滴头流量、水质、灌水量、灌水模式等对滴灌湿润锋推进的影响方面[4-11]。但是以上研究主要关注水平湿润锋和垂直湿润锋随时间的变化,没有定量研究湿润体整体随时间的变化关系,以及多因素耦合条件下微咸水滴灌湿润体随时间的变化关系模型。因此,本文将在室内进行不同微咸水矿化度和滴头流量下滴灌入渗试验,揭示不同微咸水矿化度和滴头流量下土壤湿润体的变化特征,建立微咸水矿化度与滴头流量耦合条件下滴灌土壤湿润体动态变化模型,以期为微咸水滴灌合理设计提供依据。
1 材料与方法
1.1 试验材料
试验所用土壤采集于山西省水利水电科学研究院节水高效示范基地,土壤取样深度0~110 cm。土壤质地为黏土,土壤容重为1.42 g/cm3,饱和含水率0.50 cm3/cm3,田间持水率为0.31 cm3/cm3。试验时,土壤经自然风干后,碾压并过2 mm筛备用,土壤初始质量含水率为3%,初始电导率为0.75 mS/cm。
本试验所用的水源由试验基地的一口深水井和一口浅水井提供,深水井井深180 m,浅水井井深80 m,浅水井地下水矿化度为5 g/L,深水井地下水矿化度为1.7g/L。本试验所用的微咸水水质是通过这两种水按照一定的比例配置而成。
1.2 试验方案
试验的目的是揭示不同滴头流量、入渗水矿化度条件下滴灌湿润体运移特性。因此,试验以滴头流量和入渗水矿化度为控制因子,其中滴头流量设3个水平:7 mL/min、9 mL/min、11 mL/min;入渗水矿化度设四个水平:1.7 g/L(淡水)、3 g/L、4 g/L、5 g/L(咸水),并设蒸馏水为对照处理,共8个处理,每个处理3 次重复。各处理滴灌水总量相同,均为1 260 mL,各处理情况见表1。
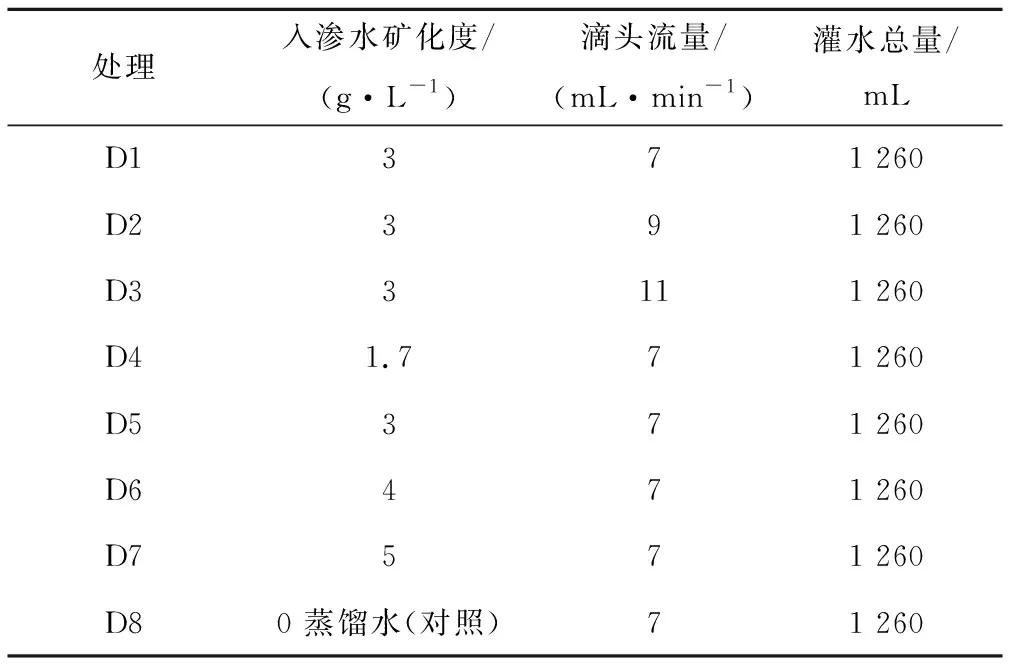
表1 试验方案
1.3 试验装置
微咸水滴灌试验装置由有机玻璃土箱和马氏瓶两部分组成。土箱的长×宽×高为30 cm×50 cm×55 cm,马氏瓶的截面积30 cm2,高度为70 cm。马氏瓶出水口和输液管连接,滴头用输液管前端的输液针模拟,装置如图1所示。
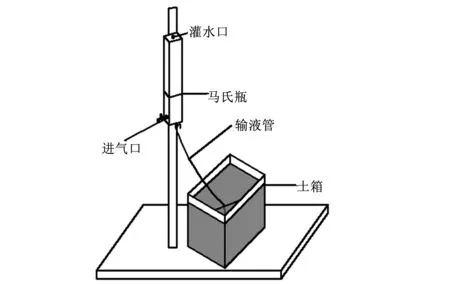
图1 微咸水滴灌入渗试验装置图
1.4 试验过程与测试项目
(1)将风干土壤按设计土壤容重,每5 cm 一层,分层装入土箱。
(2)用医用输液管连接马氏瓶出口,输液器针头模拟滴头,调节马氏瓶高度和输液器滑轮,使滴头流量与设计流量一致,并记录马氏瓶初始读数。
(3)打开马氏瓶,并用秒表开始计时,试验开始。
(4)每隔一定时间间隔,记录马氏瓶读数,并用记号笔在土箱壁上画处湿润锋,数据记录时间间隔按先密后疏原则进行。
(5)当马氏瓶供水量达到试验要求时,试验停止供水。
(6)用直尺量取并记录土箱壁上的湿润锋数据。
1.5 试验数据处理
试验采用EXCEL2016进行数据处理,采用1stopt软件进行数据拟合,采用origin9.1进行绘图。
2 结果分析
2.1 不同滴头流量下土壤湿润体特征分析
图2为微咸水矿化度3 g/L不同滴头流量条件下单点源入渗湿润锋推进图。由图2可知,各处理湿润锋的形状相似,均是以滴头为中心的1/4椭圆形,随着时间的推移,不同流量的土壤水平湿润锋推进距离和垂直湿润锋的推进距离均逐渐增大,即滴灌的湿润体体积随时间的推移而增大。对每一处理下,在相同的入渗时间,水平湿润锋的推进距离均明显大于垂直湿润锋的推进距离,这是因为试验所用的土壤为黏壤土,导致水分在水平方向运动较快,而在垂直方向运动较慢。进一步比较不同流量下湿润锋推进图可知,滴头流量越大,灌水结束时水平湿润锋推进的距离越远,垂直方向推进的距离越近,滴头流量7 mL/min、9 mL/min和11 mL/min对应的最大水平湿润锋距离分别为18、19.4和22.5 cm,最大垂直湿润锋距离分别为13.8、13.2和11.4 cm。
同时,对不同时刻湿润锋采用椭圆方程(1)进行拟合,并将拟合参数A和B随时间和流量的变化绘制为等值线图(图3)。

图2 不同滴头流量下点源入渗湿润锋推进图
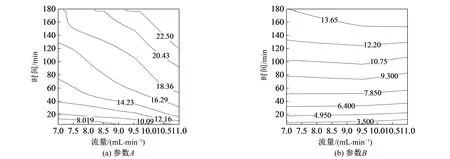
图3 不同时间和流量下土壤湿润锋参数变化图
不同流量在不同时间的湿润锋拟合的相关系数在0.94以上,说明不同滴头流量处理下不同时间的湿润锋形状可采用椭圆方程描述。参数A为椭圆的长半径,即最大水平湿润锋推进距离,参数B为椭圆短半径,即最大垂直湿润锋推进距离。同时由图3可知,随着时间和流量的增大,参数A和B均增大。
(1)
进一步,将参数A和B与时间和流量的关系,用乘幂函数拟合,拟合结果见式(2)和式(3)。由式(2)和式(3)可知,拟合相关系数在0.986以上,说明参数A和B与流量和时间符合乘幂关系。
A=0.899q0.81t0.267(R=0.986)
(2)
B=1.224q0.01t0.465(R=0.995)
(3)
式中:q为滴头流量,mL/min;t为时间,min。
2.2 不同微咸水矿化度下滴灌土壤湿润体特征分析
图4为不同微咸水矿化度(0、1.7、3、4和5 g/L)条件下单点源入渗湿润锋推进图。由图可知,各矿化度处的理湿润锋形状相似,均是以滴头为中心的1/4椭圆形,随着入渗时间的增加,各处理的水平湿润锋推进距离和垂直湿润锋的推进距离均逐渐增大,即湿润体体积随入渗时间的增大而增大。对每一处理下,在相同的入渗时间,水平湿润锋的推进距离均明显大于垂直湿润锋的推进距离,这是因为试验所用的土壤为黏壤土,导致水分在水平方向运动较快,而在垂直方向运动较慢。进一步比较不同矿化度下湿润锋推进图可知,随着矿化度增大,水平湿润锋最大推进距离先减小后增大,垂直湿润锋最大推进距离先增大后减小。这可能由两方面原因造成,一是因为采用微咸水滴灌使土壤中盐分增大,土壤颗粒更容易絮凝和形成团粒结构,土壤大孔隙增多,入渗能力变强,水分更容易向下运移,因此垂直方向运移更快;二是因为入渗水矿化度越高,进入到土壤中的钠离子越多,而钠离子增多会使土壤胶体分散度加大,影响团粒结构形成,使土壤导水能力下降,入渗能力变小,垂直方向相对运动变慢[12,13]。在这两方面原因的共同作用下,导致灌溉水矿化度小于3 g/L时,矿化度越大,水平湿润锋越小,垂直湿润锋越大;灌溉水矿化度大于3 g/L时,矿化度越大,水平湿润锋越大,垂直湿润锋越小。
对不同时刻湿润锋采用椭圆方程(1)进行拟合,并将拟合参数A和B随时间和矿化度的变化绘制为等值线图5。不同微咸水矿化度在不同时间的湿润锋拟合的相关系数在0.94以上,说明不同微咸水矿化度处理下不同时间的湿润锋形状可采用椭圆方程描述。由图5可知,参数A和B均随着时间的增大而增大,参数A随着微咸水矿化度的增大,呈先减小后增大的变化趋势,参数B随着矿化度的增大呈先增大后减小的变化趋势。

图4 不同微咸水矿化度单点源入渗湿润锋推进过程
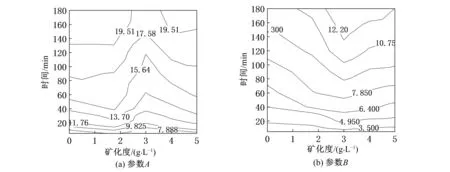
图5 不同时间和流量下土壤湿润锋参数变化图
进一步,将参数A和B与时间和流量的关系,采用式(4)和式(5)拟合。由式(4)和式(5)可知,拟合相关系数在0.965以上,说明参数A和B与流量和实际符合乘幂关系。
A=0.04[(C-3.021)2+115.126]t0.283(R=0.965)
(4)
B=-0.028[(C-3.421)2-45.849]t0.489(R=0.993)
(5)
式中:C为微咸水矿化度,g/L;t为时间,min。
2.3 微咸水矿化度与滴头流量耦合下土壤湿润体动态变化模型分析
由前分析可知,不同滴头流量和不同微咸水矿化度条件下土壤湿润锋变化均符合椭圆方程,且参数A和B分别与时间和流量或时间和矿化度有函数关系。因此,将滴头流量和微咸水矿化度对参数A和B的交互影响用乘法效应表示,构建微咸水矿化度和滴头流量耦合下的湿润体动态函数如式(6)所示。
(6)
式中:a1、b1、c1、d1、e1、a2、d2、c2、d2、e2为方程拟合参数。
为率定和验证式(6)的正确性,将试验实测的633组湿润锋数据,按4比1随机分两组,即训练集475组,验证集158组。训练集用于率定模型参数,验证集用于验证模型正确性。将训练集数据带入式(6)拟合得到参数a1、b1、c1、d1、e1、a2、d2、c2、d2、e2分别为0.060、0.464、3.567、36.785、0.242、-0.020、0.163、3.624、-40.179、0.473。
图6为模型预测湿润锋与实测值的相关性分析,由图可知在训练集和验证集,湿润锋的实测值和模拟值均线性相关,相关系数在0.98以上,这说明模型计算的湿润锋与实测值具有较好的一致性。
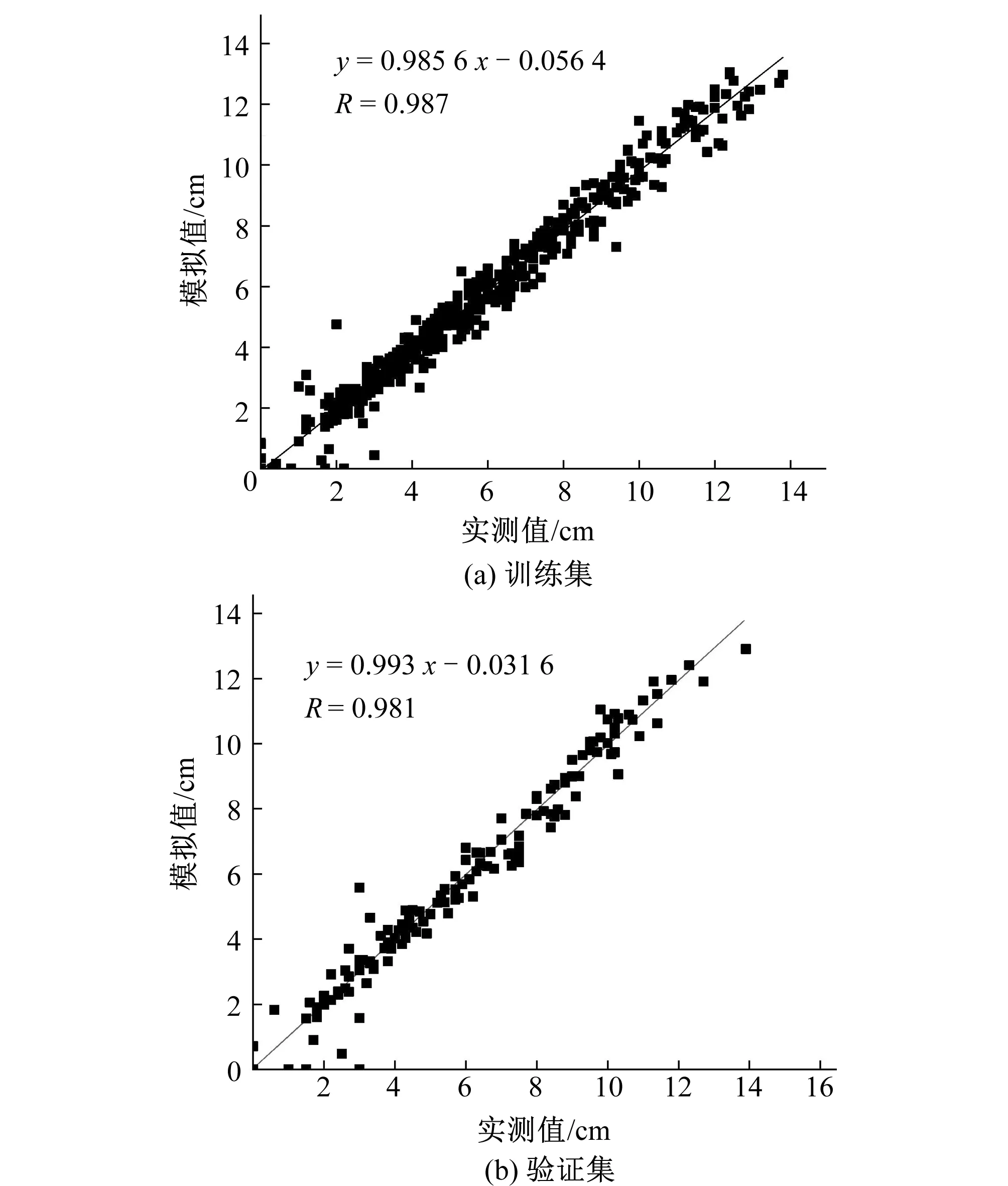
图6 模型预测值与实测值相关性分析
为了进一步评价模型的预测性能,采用平均绝对误差MAE和均方根误差RMSE对模型进行评价,其计算公式分别为
(7)
(8)
式中:LS,i为模型计算湿润锋,cm;LR,i为实测湿润锋,cm;N为实测点总数。
经计算,训练集模型的MAE和RMSE分别为0.390和0.549,验证集模型的MAE和RMSE分别为0.438和0.635,这表明本文所建立的模型有较高的计算精度,可以用于微咸水矿化度和滴头流量耦合下的湿润体动态模拟。
3 结 论
本文通过对不同微咸水矿化度和滴头流量下土壤湿润锋动态分析,得出以下结论:
(1)不同滴头流量和微咸水矿化度下滴灌土壤湿润锋形状相似,均呈1/4椭圆形,湿润锋均随着时间的增大而增大。滴头流量对湿润锋的推进距离有明显影响,滴头流量越大,水平湿润锋推进越快。矿化度也对湿润锋有明显影响,水平湿润锋随着微咸水矿化度增大,先减小后增大;而垂直湿润锋随着微咸水矿化度增大,先增大后减小。
(2)不同微咸水矿化度和滴头流量下土壤湿润锋均可采用椭圆方程拟合,在分析微咸水矿化度、滴头流量和时间对参数A和B的影响基础上,建立了微咸水矿化度和滴头流量耦合条件下滴灌土壤湿润锋动态变化模拟,并采用试验数据进行验证,表明该模型具有较高的模拟精度,可用于不同流量、不同矿化度和不同时间滴灌湿润锋的预测。
