基于广义位移法的薄壁结构超单元建模方法
2018-12-26王志瑾KretovAnatolii
原 潇,王志瑾,夏 津,Kretov Anatolii
(1. 南京航空航天大学,飞行器先进设计技术国防重点学科实验室,南京,210016;2. 上海机电工程研究所,上海,201109)
0 引 言
飞行器结构中广泛采用大长细比的薄壁梁结构型式,如机身、机翼。对类似结构进行准确的强度计算分析是非常复杂并且耗时耗力的事情。在计算机技术出现之前,要对这样的结构进行分析计算,经常采用一系列假设,通过工程模型得到近似解。随着计算技术和数值计算方法的快速发展,解析法和近似法逐渐被有限元方法取代。采用有限元方法对结构进行应力应变状态分析前,一般先对结构进行必要的简化,建立等效的有限元数学模型[1,2]。然而,有限元模型中包含大量的结构信息数据,在初始设计阶段,无法给出完整的结构信息。另外,在结构选型阶段,还需要通过初始的计算分析对结构布置提供参考依据。因此,建立简单、高效、可靠并有足够计算精度的数学模型仍然是非常必要。
在超单元法中,整体结构被分为若干个超单元,每个超单元可以视为一系列有限元素的集合。超单元法通过对系统自由度进行减缩,从而大幅减少计算量,适用于大型复杂结构的分析[3]。Guyan[4]将结构自由度分为主自由度和副自由度,通过强制忽略副自由度的影响,对刚度矩阵和质量矩阵进行缩聚,适用于静力分析和低阶模态分析;陈国平[5,6]将界面自由度和内部自由度均进行减缩,提出了适用于结构动特性分析的超单元法;在静力学领域,Ireneusz Kreja[7]提出一种梁超单元,适用于具有对称开剖面的薄壁梁结构;康龙辉[8]提出了适用于恒定截面薄壁结构静力分析的超单元法,但只适用于无锥度的薄壁结构。
本文针对具有锥度的薄壁梁结构,基于横截面内刚性假设,将节点位移缩聚为广义位移,对于3种简化模型分别推导出超单元刚度矩阵,通过Matlab编写相应求解程序。通过3个算例结果与有限元结果的对比,验证了该方法的准确性和有效性。
1 薄壁梁中的超单元法
薄壁梁结构一般由板、杆组成,可以有任意横剖面形状,其典型外形特征是大长细比的圆柱或锥形壳体。结构设计条件是满足强度和刚度要求下结构重量最轻。飞机机翼、机身,飞行器机体都是具有这种特征的薄壁梁结构,它们主要由横向构件(翼肋或框)、纵向构件(梁缘条、桁条)、腹板及蒙皮组成,如图1所示。为了建立计算模型,在横向构件处引入与xy面平行的剖面,共(c+1)个。这样,长度为 l的薄壁梁就由顺序相连的c个单元组成,每个单元的长度为le。每个横剖面同 z轴的交点就是广义节点,两个横剖面之间的一段结构实际上就是在两个剖面上具有广义位移的超单元。在对超单元进行分析时,忽略了横向构件,只考虑桁条、蒙皮、腹板的力学行为,并将桁条(缘条)等效为n个杆单元,蒙皮、腹板等效为m个板单元。

图1 典型薄壁梁结构模型Fig.1 Typical Thin-walled Beam Structure Model

续图1
根据计算精度从低到高,假设每个横剖面从绝对刚性到自由变形。假定每个剖面上的面内广义位移函数为:ϕ1(z),ϕ2(z),…,ϕM(z),面外广义位移函数为:ψ1(z),ψ2(z),…,ψN(z)。其中 M、N的值根据计算精度要求选取,且Mmin=3,Mmax=m;Nmin=3,Nmax=n。剖面上任意节点k的位移分量可以表示为
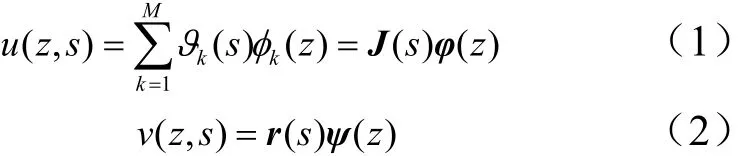
式中 z为与横剖面垂直的坐标轴;s为与横剖面轮廓相切的方向;函数ϕ(z),ψ(z)为寻找的广义位移列向量,仅与坐标z相关。横向和纵向分布函数J(s),r(s)为广义坐标s的函数。
2 超单元刚度矩阵
2.1 无锥度结构
直翼盒模型如图2所示。蒙皮和腹板简化为受剪板,纵向筋条受轴向拉压。
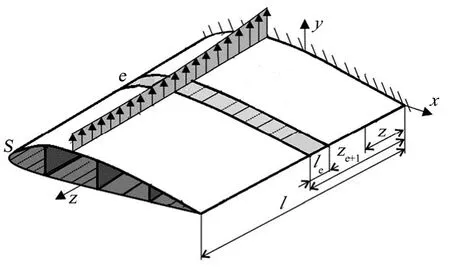
图2 直翼盒模型示意Fig.2 Diagram of Straight-wing Box Model
模型中,M=3,N=n,即每个截面具有平面内分别沿x轴和y轴的平动自由度ϕ1,ϕ2,绕z轴的转动自由度ϕ3以及 n个节点分别沿 z轴的平动自由度ψ1,ψ2,ψ3,…,ψn。相应地,ϕ1,ϕ2,ϕ3分别对应于截面上的广义集中力 Qx,Qy,Mz,ψ1,ψ2,ψ3,…,ψn对应的广义力为作用在相应节点的沿z轴方向的集中力Z1,Z2,Z3,…,ZN。
由于结构没有锥度,所以每根杆的长度相同,且杆轴向与整体坐标系 z轴平行,故沿杆轴向的积分可以转换为沿 z轴的积分,同时可以交换积分与求和的顺序。
对第i根纵向筋条:

对第j块板:
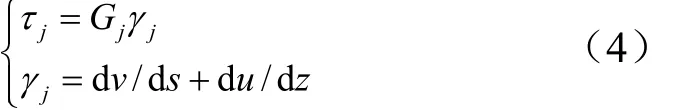
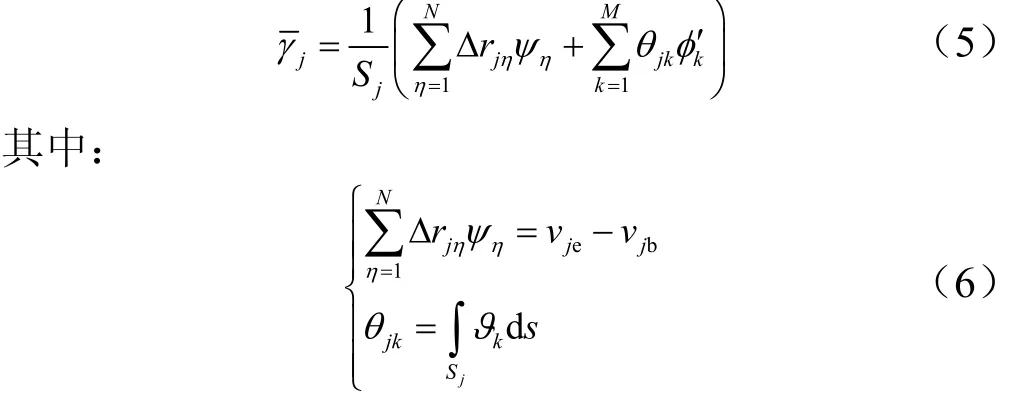
式中 Sj为第j个板单元沿着s方向的长度;vje和vjb分别表示板单元末端节点和起始端节点在 z轴方向上的位移。
写出由n个杆单元和m个板单元组成的第e个超单元的应变能和外力功并进行变分,以矩阵形式表示如下:

在一个超单元范围内,认为可能的位移及虚位移ϕ(z)、ψ(z)、δϕ(z)、δψ(z)符合线性变化规律,即:

将式(9)代入式(7),根据线性位移假设进行积分。根据能量原理:δAe=δUe,经过整理得到:

对于小锥度结构,需要对式(11)中的广义力向量进行修正:
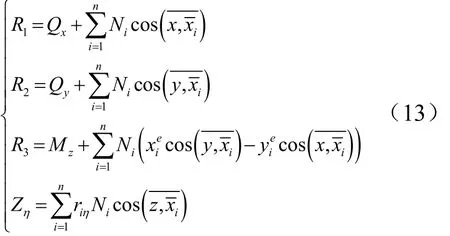
得到单个超单元的刚度矩阵后,按照图3所示的方式进行组集,即可以得到整个结构的刚度矩阵。

图3 面内刚性假设下小锥度结构刚度矩阵组装Fig.3 Assembly of Stiffness Matrix of Small Taper Structure under the Assumption of Cross-section Rigidity
2.2 梯形平面正应力板
实际计算时,当无锥度或者结构锥度很小时,符合2.1节中对应的情况,当锥度较大时,就必须有另外的方法。
与此相关的主要问题就是要求解四边形板的刚度矩阵。借助有限元中的经典方法,用4个三角形代替四边形,如图4所示。

图4 大锥度盒段模型示意Fig.4 Diagram of Large Taper Box Segment Model
在局部坐标系下杆元的刚度矩阵[9]为

在局部坐标系下,对 4个三角形单元刚度矩阵组集,就得到四边形单元的刚度矩阵,它有5个节点:

由于中心5号节点没有节点力,根据此条件,基于式(15),可以得到5号节点位移与其余4个节点位移之间的关系,进一步得到4节点四边形平面应力板的刚度矩阵:

对节点力和位移进行坐标矩阵变换,就将刚度矩阵从局部坐标变换成了总体坐标。
对于杆:

对于板:
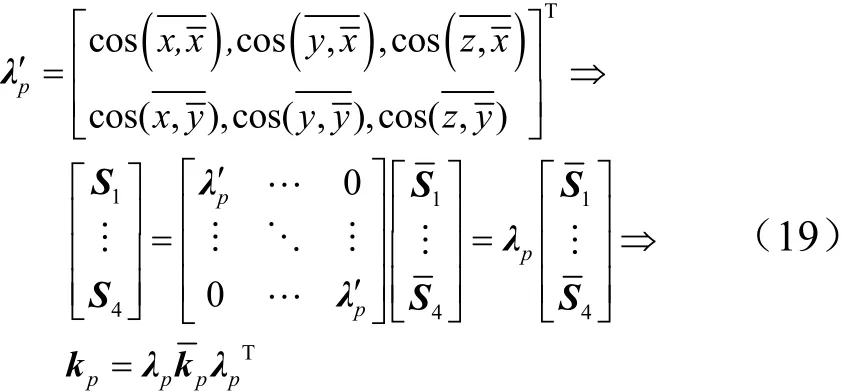
根据上一步结果,基于节点力平衡原则,将 n根杆和m块板的刚度矩阵在整体坐标系下进行组集,得到第e个超单元以有限元法为基础的刚度矩阵,即:
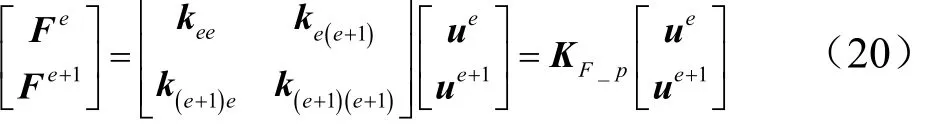
式中 ue,ue+1分别对应于 e和 е+1剖面的位移向量;Fe,Fe+1为相应的节点力向量。
将超单元两端面的真实位移转换成广义位移:ϕe、ψe和ϕe+1、ψe+1分别为剖面 e和 e+1的广义位移向量;Re、Ze和Re+1、Ze+1分别为剖面e和e+1的广义力向量。
在超单元剖面上,真实位移和广义位移之间、广义力和真实力之间的关系分别为

式中 Т为位移转置矩阵;λ为力转置矩阵。
且有:


最终,对每个超单元,有以下表达式:
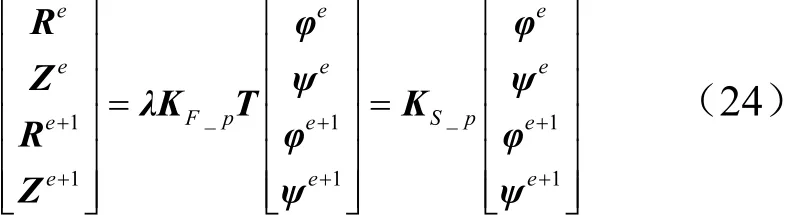
式中 KF_p为对应于节点力、节点位移的刚度矩阵;KS_p为对应于超单元广义力、广义位移的刚度矩阵。
由于每一个剖面只有 3个面内自由度,N个面外自由度,则通过真实位移向广义位移转换,超单元的刚度矩阵阶数由 6n×6n降为 2(3+N)×2(3+N)。
2.3 梯形受剪板
2.2 节中超单元刚度矩阵的计算工作量很大,对于需要多次迭代的设计和优化过程不方便也不可取。基于此,设想用更简单的方法形成板的刚度矩阵,假设此时板只受剪切。
梯形受剪板如图5所示,其板厚为t,剪切弹性系数为G。取梯形板4个角点为节点,分别记为1、2、3、4。图中表示节点i的节点力。

图5 受剪梯形板刚度矩阵简化方式Fig.5 Simplified Method of Stiffness Matrix of Shear Trapezoidal Plate
文献[9]中给出了梯形受剪板在整体坐标系下的刚度矩阵:

其中,

类似于2.2节,每一超单元的刚度矩阵由n根杆和m块板的刚度矩阵按照节点力平衡原则进行组集,然后通过广义坐标变换得到。

式中 KF_sp为对应于节点力、节点位移的刚度矩阵;KS_sp为对应于超单元广义力、广义位移的刚度矩阵。
3 不同模型的计算比较
3.1 四梁盒段
盒段的形状、尺寸、载荷如图6所示,材料为铝合金,弹性模量E=72 GPa,泊松比µ=0.33。

图6 算例1模型示意Fig.6 Diagram of Example1 Model
模型1、模型2和模型3是分别对应2.1,2.2,2.3节所提出的建模方法,采用Matlab语言编写相应程序得到的计算结果。为了便于比较,也利用通用有限元软件ABAQUS对该算例进行了计算。式(28)为本算例采用虚力原理得到的解析解[10]。

式中 第1项为弯曲引起的变形,第2项为剪切引起的变形。
图7给出了采用各种计算模型和方法所需的计算时间(以ABAQUS为基准)。采用模型1计算最快,模型3与ABAQUS相当,模型2计算时间显著高于其它模型和方法。图8给出采用模型1、模型2、模型3、锥度角β=0°时单个超单元长细比对计算误差的影响。当结构的总长度一定时,从图8可以看出,随着超单元个数的增加,即单个超单元长细比的减小,结构最大位移的计算精度逐渐提高,即可通过控制单个超单元长细比(超单元个数)来获得不同的计算精度。同时,模型1与模型3在锥度角β=0时计算结果的精度相当,且均低于模型2的计算精度。图9给出了采用模型2、模型3时,结构锥度角对计算误差的影响。从图9中可以看出,超单元法的计算精度随着结构锥度角的增加而下降。
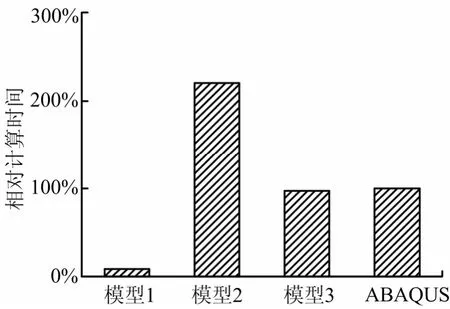
图7 各计算方法计算时间比较Fig.7 Comparison of Calculation Time of Each Calculation Method
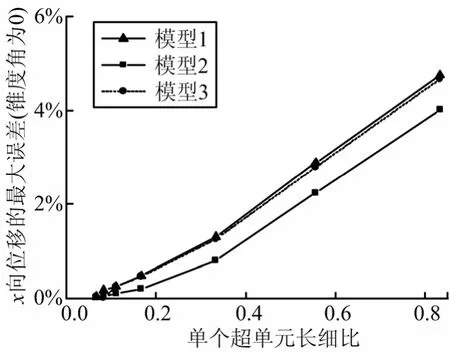
图8 锥度角为0时计算误差与单个超单元长细比的关系Fig.8 Relationship Curve between the Calculation Error and Long Fineness Ratio of a Single Superelement at a Taper Angle of 0°

图9 计算误差与锥度角的关系Fig.9 Ralationship Curve between Calculation Error and Taper Angle
3.2 小展弦比后掠翼
该算例为带4根梁和3组桁条的后掠机翼。结构的外形、尺寸及载荷见图10,材料为铝合金,弹性模量E=72 GPa,泊松比µ=0.3;梁缘条面积为173 mm2,外面两组桁条的面积为50 mm2,中间一组桁条面积为76.4 mm2,蒙皮和腹板厚度为3 mm。在结构端部施加集中力Qy,大小为15 000 N,与y轴平行。
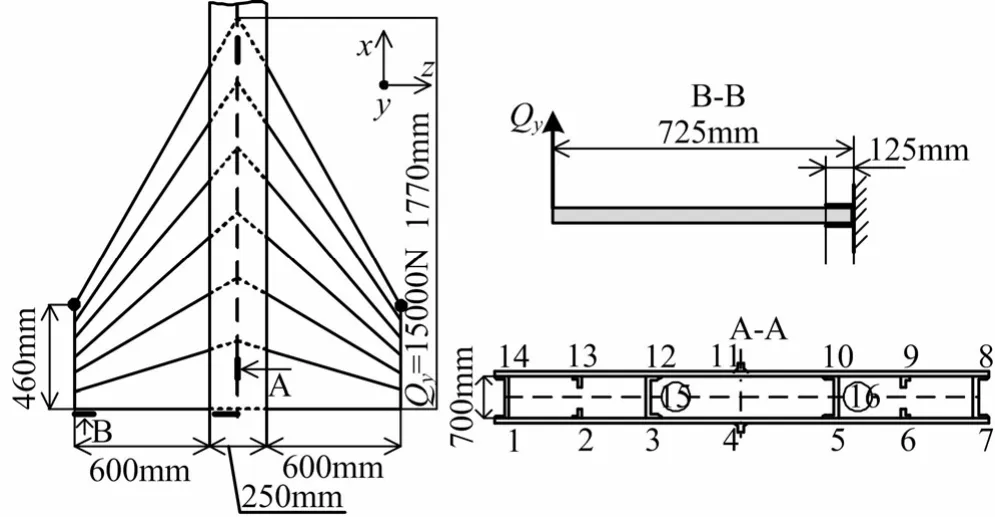
图10 后掠翼示意Fig.10 Rear Wing Diagram
文献[11]中给出了这个结构的试验结果以及计算结果;模型1中,计算板刚度矩阵时采用2.2节方法,即将蒙皮和腹板当作平面应力板处理;模型2中,把板当作受剪板处理,此时必须把板的面积(20~30δ2)等效到两边的筋条上。图11给出了沿结构展长方向各方法得到的位移对比。模型 1的计算结果与文献[11]值大致相当,而最大位移值较文献值更接近试验值。与试验值相比,模型2计算结果最大误差为7.7%,计算精度低于模型1的最大误差5.8%。

图11 沿展长方向y向位移计算结果对比Fig.11 Comparison of the Calculation Results of y-direction Displacement Along the Length of the Exhibition
3.3 小锥度机身盒段
该小锥度机身段长度为8 m,半径由0.6 m过渡到0.75 m,其示意见图12。沿机身轴向分布24根长桁,其横截面积为50 mm2;蒙皮厚度为1.6 mm,材料为铝合金,弹性模量 E=72 GPa,泊松比 µ=0.3。从机身固支端起沿机身长度方向,每隔0.5 m,在横截面上施加大小为4000 N的集中力Qy,总载荷大小为64 000 N。将机身沿长度方向划分为16个超单元。

图12 小锥度机身盒段示意Fig.12 Diagram of Small Taper Fuselage Box Segment
模型1、模型2分别对应于应力板和受剪板两种简化方式。将 Matlab程序求解结果与有限元软件ABAQUS分析结果进行比较,沿机身长度方向横截面y向位移结果对比见图 13。由计算结果可知,两种模型的计算结果与有限元分析结果相接近,模型1横截面y向最大位移的计算误差大于模型2,为3.2%。则超单元法亦适用于机身类薄壁结构。沿着结构的长度方向,超单元法的计算误差逐渐增大。对于大长细比的薄壁结构,可以通过增加超单元的划分个数(即减小单个超单元的长细比)来提高超单元法的计算精度。

图13 沿机身长度方向y向位移计算结果对比Fig.13 Comparison of the Calculation Results of y-direction Displacement Along the Length of the Fuselage
4 结 论
本文提出的针对大长细比薄壁结构的超单元建模方法,单元数量少,刚度矩阵阶数低,可以大大减少数据准备工作量,减少人力消耗。同时超单元方法的计算精度可以根据不同位移假设依次提高,适合不同设计阶段的精度要求。对于3种设计模型,2.1节中的模型和2.3节中模型计算效率高,2.2节中的模型给出的结果精度最高,但计算效率相对较低。3种模型都可以有效地用于实际结构设计中。
