二次函数在生活中的应用

邓革周

二次函数在生活中的应用，主要涉及到商品利润、几何图形的最值和判断说理等方面.下面举数例加以说明，供你学习时参考.

一、抛物线形问题

例1某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图1所示，以水平方向为x轴、喷水池中心为原点建立直角坐标系.

（1）求水柱所在抛物线（第一象限部分）的函数表达式；

（2）王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅必须站在离水池中心多少米以内？

（3）经检修评估，游乐园决定对喷水设施做如下改进：在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后喷水池水柱的最大高度.

解：（1）设水柱所在抛物线（第一象限部分）的解析式为y越a（x-3）2+5（a≠0），

将（8，0）代入y越a（x-3）2+5，得

点评：利用二次函数解决抛物线形的喷泉、隧道、大桥和拱门等实际问题时，要把实际问题中的数据转化为抛物线上的点，从而确定解析式，通过解析式去解决问题.

二、商品利润问题

例2“扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售y（件）与销售单价x（元）之间存在一次函数关系，如图2所示.

（1）求y与x之间的函数关系式；

（2）如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？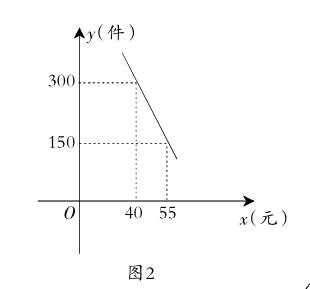

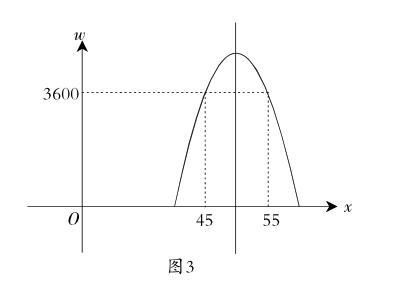
（3）该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3600元，试确定该漆器笔筒销售单价的范围.

分析：（1）可用待定系数法确定y与x之间的函数关系式；

（2）根据“利润=销售量×单件的利润”，结合（1）中的函数关系式，求出利润和销售单价之间的关系式，根据函数性质来求最大利润；

（3）建立利润w与x的函数关系式，进而利用所获利润等于3600元时，求出对应x的值，根据增减性，求出x的取值范围.

点评：在生产经营活动中，经常会遇到求最大利润、最大销量等问题.解此类题的关键是确定二次函数的解析式，根据函数性质确定其最大值.自变量x的取值要使实际问题有意义.如本题第（2）题，如果不注意自变量的取值范围，将x=50代入求最值就错了.

三、判断说理问题

例3某农场拟建一间矩形种牛饲养室，饲养室的一面靠墙（墙足够长），已知建筑材料可建围墙50m.设饲养室长为x（m），占地面积为y（m2）.

（1）如图4，问饲养室长x为多少时，占地面积y最大？

（2）如图5，现要求在图中所示位置留2m宽的门，且仍使饲养室的占地面积最大.小敏说：“只要饲养室长比（1）中的长多2m就行了.”请你通过计算，判断小敏的说法是否正确.

∴小敏的说法不正确.

点评：解一边靠墙围矩形场地的面积问题，用自变量表示矩形的长和宽，根据矩形的面积公式得出函数关系式是解题的关键.在几何图形中，二次函数问题常见的有：面积的最值、用料的最佳方案以及動态几何中的最值.