基于关系曲线特征分析的水轮机组故障诊断方法

蔡金华，陈 俊，牛洪海，蔡 丹，徐卫峰

（南京南瑞继保电气有限公司，江苏省南京市 211102）

0 引言

水轮发电机组故障诊断是水电厂状态检修的重要内容，是智能化水电厂的重要课题之一，然而，水轮发电机组是一个复杂耦合的非线性动力系统，水轮发电机组故障受到水、机、电等多种因素的复合作用影响，不同故障有不同的电气、机械表征，包括机组振动强度与机组转速、负荷、流量等参数的不同映射关系，机组振动与工况参数间的幅值关系一直是振动故障的重要关联性征兆。

不少学者[1，2]通过对振动强度与转速、压力、负载以及流量间的幅值进行相关性分析，然后通过相关系数反馈故障特征。然而，相关系数仅仅衡量了目标变量之间的线性相关程度，而机组振动强度与诸多状态参量幅值之间的关系具有明显的非线性特点，仅仅通过相关系数难以对机组振动与工况参数间的复杂映射关系进行准确、全面地描述。有研究表明[3]，振动转速关系曲线中蕴含着大量的机组故障信息，其形状特征与故障类型存在着一定的映射关系，比如：不平衡故障所对应的振动转速关系曲线呈现出明显的上升趋势；机组出现轴瓦问题时，振动强度随着转速增大会出现明显的阶跃上升趋势；压力脉动所引起的振动则随转速变化较小。综上所述，根据振动转速关系曲线的形状特征能够对机组故障进行识别诊断。因此，本文以机组振动—转速幅值关系曲线来表征机组运行状态信息，通过自动识别关系曲线的形状特征[4]，辅助判断机组故障原因，为机组故障关联性征兆的获取提供了一种新思路。

1 振动转速关系曲线

水轮发电机组振动转速关系曲线是由具有一一映射关系的振动幅值序列和机组转速序列联合绘制而成。图1给出了水轮发电机组振动转速关系曲线测量系统及绘制原理的示意图。

根据美国学者J.S.Sohre和C.Jackson的“旋转机械振动分析征兆一般变化规律表[3]”，不同的故障通常会反映出不同形状的振动转速关系曲线，而各种不同形状的曲线总体归纳为振幅不变、随转速上升、随转速下降、突然上升、突然下降和出现峰值6种，如图2所示。

本文从“旋转机械振动分析征兆一般变化规律表”中节选出了初始不平衡、密封摩擦、油膜涡动、压力脉动等几种典型故障与振动转速关系变化曲线的对应情况，如表1所示。

图1 水轮发电机组振动转速关系曲线测量及绘制示意图Fig.1 The diagramming of Hydro turbine vibration-speed relation

图2 振动转速关系曲线的6种标准形状Fig.2 Six standard shapes of of Hydro turbine vibration-speed relation

表1 典型故障与振动转速关系曲线形状对应情况Tab.1 The congruent relationship between typical fault and the vibration-speed relation curve

振动转速关系曲线具有以下特点：

（1）简单性。振动转速关系曲线为非闭合曲线，关系曲线中噪声干扰相对较小。

（2）函数性。振动转速关系曲线由振动与转速序列绘制而得，因此，曲线上每个转速点对应且只对应一个振动幅值点，曲线可由函数A=f（n）表示，n为水轮机转速，单位为r/s；A为水轮机振动幅值，单位为μm。

（3）旋转可变性。振动转速关系曲线的斜率直接决定着其形状，因此，特征提取方法在具有缩放、平移不变性的同时，需要对旋转变换极为敏感，具有旋转可变性。

2 振动转速关系曲线形状特征识别

2.1 非闭合曲线的区间矢量特征编码

本文基于矢量特征编码（Interval vector feature coding），自动识别振动转速关系曲线，表征曲线的形状特征。起始点根据编码方向进行选择，从起始点开始对曲线上各点依次编码，直至曲线另一端点位置，获得非闭合曲线的链码表示。

图3 区间矢量特征编码Fig.3 Statistical vector chain code

传统的Freeman链码利用曲线起始点坐标与一系列边界顶点的方向代码对多边形边界进行表征[5]，其定义如下：

其中：S为所选起始点的坐标，（i=1，2，3，...，n）代表着各个边界点的方向编码序列。编码方式分为4连通编码、8连通编码两种[6]，具体如图3所示为一简单非闭合曲线的Freeman链码编码示例，采用8连通编码规则。编码前需要对图形进行栅格化处理，从而得到边界点序列，而像素点的划分却缺乏统一的标准，不同的划分方式会得到截然不同的编码结果。选定起始点之后，各边界点根据其相对于前一个边界点所处的位置及距离进行编码。

矢量特征编码根据多边形的内角信息进行编码，而对于振动转速关系曲线这类非闭合曲线而言，需要在编码方式方面对矢量特征编码进行改进：

首先，考虑曲线的简单性，采用二维点划分来代替栅格化中的像素点划分，由曲线上以振幅、转速为坐标的二维点序列来代替栅格化后所得边界点序列，从而避免像素划分不当对链码表征能力造成的影响；

其次，以曲线上各相邻点间的相对位置信息取代多边形内角作为编码依据，运用矢量编码规则对振动转速关系曲线进行编码；

最后，从链码中提取其统计特征，获得关系曲线的矢量特征编码特征向量。

振动转速关系曲线的编码方向从左向右，即为转速从小到大的顺序编码，曲线中除起始点以外，右边的点的转速值总是大于左边的点。那么，采用8连通编码规则进行编码，方向码只会是“2”“1”“0”“7”“6”这5个中的一个，如图3（a）所示。基于上述分析，在新的区间矢量编码规则中，将序列点Zi右方的区域划分为 5 个子区间 A1-A5，按角度划分依次为：[75，90]，（15，75），[-15，15]，（-75，-15），[-90，-75]，分别对应8连通编码中的“2”“1”“0”“7”和“6”5个方向，如图4（a）所示。而Zi的后继相邻点Zi+1必然落于5个子区间中，以直线Zi Zi+1与x轴的夹角θi为区间变量，通过区间识别分别求取Zi+1对各个子区间的隶属度，隶属度函数如图4（b）所示。考虑到突然上升、突然下降和振幅不变相对于随转速上升或下降具有更加苛刻条件，区域A1、A3、A5采用三角形隶属度函数，而A2、A4采用梯形隶属度函数[7]。

图4 矢量特征编码的改进Fig.4 Improved statistical interval vector chain code

根据上述编码规则，可对曲线上各点进行编码。第i个边界点Zi的区间矢量编码IVCi的定义如下：

其中：Li为曲线上相邻两点间连线ZiZi+1的长度，Mi为曲线上点Zi的隶属度矢量，mij为第i个边界点对区域Aj（j=1，2，3，4，5）的隶属度。

利用各曲线上各点的区间矢量编码代替传统编码，并按顺序依此链接，构成曲线的区间矢量链码（Interval Vector Chain Code，IVCC），如式（2）所示：

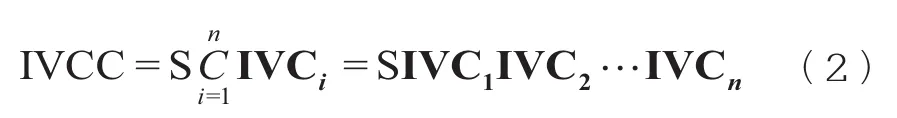
IVCC明显的不具有平移和缩放不变性，为此需要对IVCC进行一定的处理，提取IVCC中的统计信息，对曲线形状特征进行描述：

其中：L为振动转速关系曲线的长度，SUM（IVCC）为IVCC和向量，而smj为关系曲线对第j个区域Aj（j=1，2，3，4，5）的统计隶属度，表征了曲线整体处于某种变化趋势的程度，其定义如下：

显然，区间矢量特征编码具有平移和缩放不变性，振动转速关系曲线的区间矢量特征编码依据各相邻点间的相对位置信息进行编码，并非夹角信息，而点与点之间的位置信息是对旋转变换极为敏感的，因此，振动转速关系曲线的区间矢量特征编码保持着旋转可变性。

2.2 振动转速关系曲线形状特征识别

运用区间矢量特征编码提取振动转速关系曲线的形状特征，首先需要分别对振幅和转速序列进行归一化处理，构成标准化的振动转速关系曲线。基于区间矢量特征编码的振动转速关系曲线形状特征提取具体步骤如下。

步骤1：测量不同转速下的振动幅值，对振幅和转速序列分别进行归一化处理，获得标准化的振动转速关系曲线。

步骤2：对振动转速关系曲线进行二次抽样，减少序列点数。

步骤3：计算各序列点的矢量码。

步骤4：依据各点编码，求得曲线的区间矢量特征编码。

步骤5：最终得到振动转速间关系曲线的形状特征向量。

表2中列出了图2中所示6种标准振动转速关系曲线所对应的区间矢量特征编码特征向量，可以看出，不同曲线的区间矢量特征编码差别明显，能够有效表征不同曲线的形状特征。

本文通过仿真试验对所提区间矢量编码的有效性进行检验，首先运用SIVCC提取曲线形状特征，之后根据所得特征向量，采用支持向量机[8，9]对曲线形状进行识别。图5给出了振动转速关系曲线自动识别的流程。

表2 6种标准振动转速关系曲线所对应的特征向量Tab.2 Characteristic vectors corresponding to six standard vibration-speed relation curves

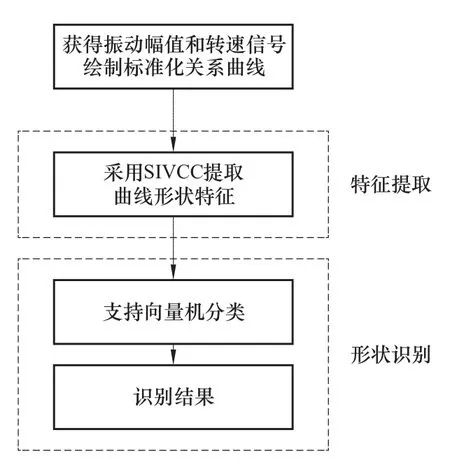
图5 振动转速关系曲线识别流程图Fig.5 The flow chart of vibration-speed relation curve identification

3 实例分析

如图6所示，以二滩水电站3号机组为例，对其振动转速关系曲线进行分析。

图6 二滩水电站3号机组开机过程振动与转速关系曲线Fig.6 The vibration-speed relation curve during start-up of no.3 unit in Ertan hydropower station

运用本章所提方法提取其形状特征并完成曲线类型识别，结合机组实际状况，对基于区间矢量特征编码的振动转速关系曲线自动识别在实际工程应用中的有效性进行检验[10]。根据3号机组振摆系统历史监测数据，上导摆度明显强于其他机组，且经常会超出预设的摆度报警值（180μm）。通过机组开机过程记录，获得上导摆度随转速上升的变化过程，如图2所示，属于6种标准关系中的“随转速上升”。

运用本章所提出的区间矢量特征编码对上述曲线形状特征进行提取，所得特征向量如表3所示，对比6类标准曲线形状特征，明显与“随转速上升”一类曲线更为接近。以仿真试验中训练后的支持向量机为模型，以4次开机过程中的振动转速关系曲线为测试样本进行测试，所得结果如表4所示。

4组振动转速关系曲线对“随转速上升”类的隶属概率均超过了90%，因此经支持向量机分类[11]，识别为“随转速上升”，与实际情况一致。根据表1可知，初始不平衡故障所对应的振动转速关系曲线100%呈现出振幅随转速上升趋势，进而可以判断3号机组存在不平衡故障的概率较大，该结论与3号机组综合分析结果相符。同时，值得注意的是，密封摩擦故障也有约70%概率会呈现出振幅随转速上升趋势，因此，仅通过振动转速关系曲线形状来判断，该故障也有可能存在。由此可见，依靠单一故障特征很难对机组进行全面准确的故障诊断，同时运用机组故障的多元征兆进行综合诊断具有着重要意义。

表3 二滩水电站3号机组振动转速关系曲线特征向量Tab.3 The characteristic vectors of the vibration-speed relation curve during start-up of No.3 unit in Ertan hydropower station

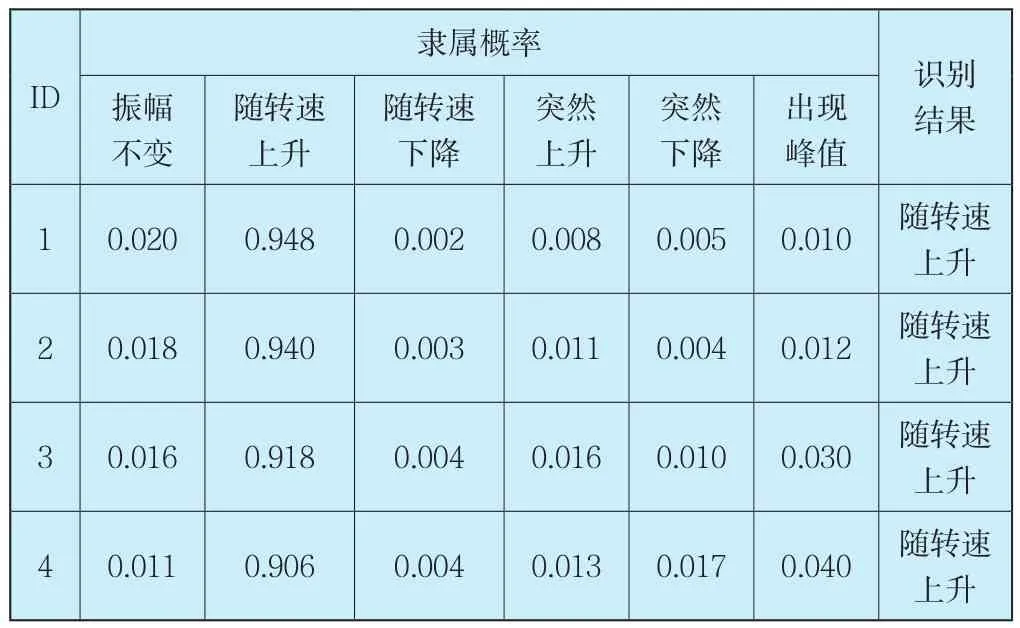
表4 二滩水电站3号机组振动转速关系识别结果Tab.4 The results of Relation Curve Characteristics Extraction during start-up of No.3 unit in Ertan hydropower station

4 结束语

本文通过改进非闭合曲线编码规则，提出了一种基于区间矢量特征编码的关系曲线自动识别方法，实现水轮发电机组振动与转速间的幅值关系曲线的特征识别，该方法通过关系曲线上各相邻点间的相对位置完成矩阵编码，通过6类标准振动转速关系曲线，以此为样本对所提方法的有效性进行验证。进一步工程实例应用分析，获得了与综合分析一致的结果，验证了该方法的工程实用价值。综上所述，本章所提方法能够通过振动转速关系曲线特征提取实现水轮发电机组的故障判断，有助于智能化水电站的发展。