拟态多执行体架构下的超时阈值计算方法

2018-12-25聂德雷赵博王崇汪欣燕昺昊

网络与信息安全学报 2018年10期

聂德雷，赵博，王崇，汪欣，燕昺昊

拟态多执行体架构下的超时阈值计算方法

聂德雷1，赵博2，王崇2，汪欣3，燕昺昊2

（1. 天津市滨海新区科技和工业创新委员会，天津 300000； 2. 国家数字交换系统工程技术研究中心，河南郑州 450002； 3. 天津滨海新区信息技术创新中心，天津 300000）

针对当前超时策略算法难以应对任务量起伏剧烈情况的问题，提出了一种应用于拟态防御架构系统的基于等效比例执行时间的超时阈值预测算法，利用拟态防御架构中多个功能等价执行体任务执行时间正相关的原理，预测任务执行时间并设置合理的超时阈值。仿真结果表明，所提算法能够针对不同任务情况动态地预测并设定超时阈值，有效地提高了超时判决效率，尤其适用于任务量变化剧烈的场景。

拟态防御；阈值计算；多执行体；超时判决

1 引言

随着网络技术的不断发展，网络空间安全的重要性愈发凸显。拟态安全防御是一种应对网络攻击威胁的新思想，其通过构建动态异构冗余的系统架构和运行机制实现“容侵”[1-3]。在拟态防御系统中，拟态调度器从异构冗余池内动态选择多个异构功能等价执行体进行任务分配，各执行体将处理结果输出给仲裁器进行仲裁，得到最终结果。

虽然异构功能等价体在设计过程中尽可能保持功能等价性能接近，但在实际环境中面对不同任务时，处理效率无法保证完全一致，故仲裁器需要等待所有执行体处理完毕并输出结果才可进行一致性裁决。若存在某个执行体受到攻击、非法操控或者随机失效而无法产生有效输出或任务执行时间显著延长的情况，将导致仲裁器陷入长时间等待，甚至致使其他执行体无法继续执行后续任务，不仅增加系统时间开销，而且严重影响系统的正常运行。因此，在系统构建中引入超时机制来限制异构体执行任务的最长时间，这对于提高系统仲裁效率、保障系统正常运行具有重要意义。

针对超时机制问题，Ryu等[4]提出了一种基于测量的二进制指数超时（MBET, measurement- based binary exponential timeout）策略，令每个流的超时相互独立，先设定一个足够大的超时参数，然后在每个超时时间内观测流吞吐量并调整超时参数（以2的指数形式递减或维持不变），优点是可以快速得到理想的超时参数且实现简单，但没有对初始参数的设置进行讨论，且不适用于吞吐量变化较大的场景。钱迎进等[5]提出了一种基于滑动时间窗口算法的自适应超时策略，利用滑动窗口算法得到各时间段内的服务时间历史记录，并预测下一阶段的超时参数，其优点是超时参数可以根据拥塞情况动态调整，且有多种方案可以选择，但没有对拟合精度和效果进行深入讨论。周明中等[6]提出了一种两层自适应超时策略（TSAT），综合固定超时和自适应超时的优点，对于不同特点的网络流采用不同的超时策略，能有效提高系统效能，节省存储空间，但实现起来较复杂。Claffy[7]提出了一种固定超时的实现方法，虽然可以取得较好的效果，但是不具有动态性和适应性。Fonti等[8]分析了在计算机中更新应用程序超时值的机制系统。侯颖等[9]通过自适应超时技术过滤器解决网络空间拥塞问题。

通过分析发现，现有的超时机制都是使用单个处理单元或执行体，通过某种规则或计数器实现超时控制，其对超时阈值或处理时间的预测往往基于一个前提，即相邻任务的任务量接近、任务执行时间变化趋势可预测。然而在实际应用中，大量场景的任务量变化无规律可循，相邻任务的执行时间也不具相关性，此时上述阈值预测算法性能会急剧下降。本文提出了一种新的超时阈值预测（EPET，equivalent proportional execution time）算法。EPET利用执行体功能等价性原理，通过历史任务执行时间队列来近似估算执行体间的处理效率，并以完成任务的执行体为基准，预测剩余执行体的执行时间并计算超时阈值。相比已有方法，EPET不仅能够较好地应对前后任务差异较大的情况，适用于拟态防御环境，而且计算复杂度低，避免产生额外开销。

2 基于多执行体的自适应超时阈值预测算法

2.1 EPET算法

当前已有的超时阈值算法只针对单执行体情况[10-11]，利用历史任务的处理时间来预测下一任务的处理时间，并不适用于任务量变化剧烈、无规律可循的情况。拟态防御架构区别于普通系统架构的重要特征之一为包含多个异构功能等价体，存在一致性特征，即在构建拟态防御架构时选择性能相近的功能等价体，以保证运行结果的无偏性，同时便于后续裁决过程。因此对于同样的任务，多个异构执行体的处理时间较为接近，并与处理能力呈近似反比关系。进一步，在面对不同处理量的任务时，多个异构执行体的处理时间往往会呈现相同的增加或减少趋势[12]。

因此，在EPET算法中，通过利用第一个完成任务的等价体的执行时间及各执行体间的执行时间等效比例，来估算其余等价体的执行时间。即

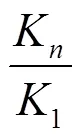
考虑到预测精度、系统负载以及传输延时等情况，最终选取的超时阈值需要对期望的任务执行耗时进行合理放大，避免由于超时阈值选取过小导致误报率增大的情况。

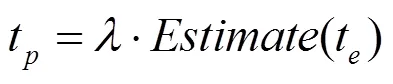
其中，t为最终选取的超时阈值，为放大系数，依据应用场景的具体需求设定，取＞1。

进一步，EPET通过对每个执行体维护一个历史任务执行时间队列来计算各执行体的执行时间等效比例。

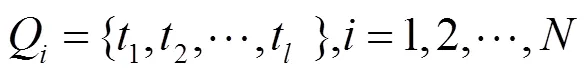
历史任务执行时间队列Q更新规则如下。

1) 若执行体为当前时刻第一个完成任务执行并输出有效结果的执行体，则将执行体的实际执行时间t加入时间队列，并将队列中最远时刻时间记录移出队列，此时，Q更新为

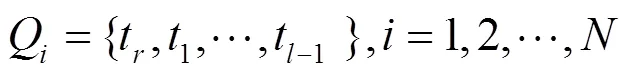
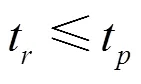
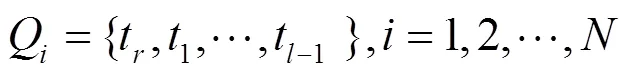
2.2 特殊性分析

本文针对拟态防御系统提出自适应超时阈值算法，本意是排除由于执行周期过长、产生随机错误或受到攻击而无法在合理时间内得到有效输出的异构执行体。然而，算法实施过程存在特殊情况，即执行体可能由于某些异常原因或受到远程控制，导致执行体未按照控制命令完整地执行相应的功能，造成执行时间显著缩短。进而在此类情况下，通过EPET算法进行异构执行体超时阈值预测将导致正常执行体全部被判决为超时，拟态防御机制失效，严重影响系统正常运行及安全性能。

为解决上述问题，此时EPET规则改进如下。

1) 根据第一个完成任务的执行体计算出超时阈值，若其他所有执行体的执行时间均超过该超时阈值，即根据该阈值其他执行体全部被判为超时，则判决此时执行体异常且预测超时阈值失效，继续等待其余执行体输出结果。

2) 若根据第二个执行体1完成任务时间计算出来的超时阈值并未导致其余执行体全部被判为超时，即存在执行体在预测阈值时间内完成任务，则判定此时超时阈值预测有效。此时以第二个执行体为基准，按照2.1节所述规则更新所有执行体历史事件队列。

3) 若根据第二个执行体1完成任务时间计算出来的超时阈值继续导致其余执行体全部被判为超时，重复上述步骤，直到有执行体在预测阈值时间内完成任务。

根据拟态防御架构原理，攻击者同时针对所有异构功能执行体完成攻击或控制仅存在理论上的可能性，在实际环境中为保证拟态防御性能异构性，执行体的研发、组成、选取、运行等过程差异显著，致使攻击者无法在短时间内利用有限的人力、物力完成对所有执行体的探测和攻击过程，因此，所有执行体都存在异常的情况不在本文算法考虑之内。

2.3 复杂度分析

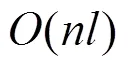
3 实验设置

为实现对本文提出的EPET自适应超时阈值预测算法进行仿真，搭建基于拟态原理构建的处理器系统，原理如图1所示。拟态处理器系统包括4个异构处理器、一个拟态调度器以及相关外围接口。其中，4个异构处理器分别为AMD、x86 i3、ARM Cortex-A9、龙芯1F(32 bit MIPS架构)，分别搭载Windows7、Windows10、Ubuntu、中标麒麟系统，独立并行处理用户端下发的指令及任务；调度模块为Xilinx Virtex-7系列FPGA，型号为XC7VX690T，主要完成对外通信接口、数据指令分发、处理结果判决、数据分组转发等任务，3个处理器模块接收调度模块发送来的数据和指令，并完成任务处理，再将结果转发给调度模块。硬件平台上，FPGA和各处理器之间的数据传输过程极短，可以忽略。仿真实验过程针对同一实验进行多次，最终结果取各次结果平均值，保证结果的无偏性。

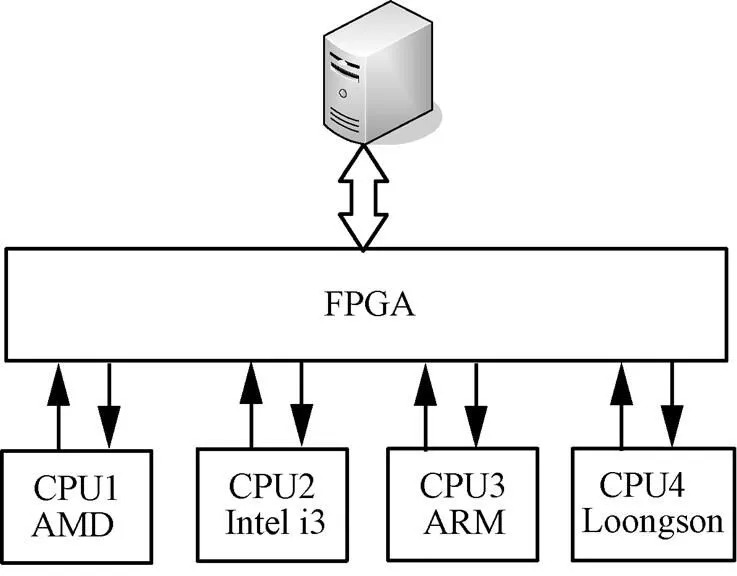
图1 拟态处理器系统原理

此外，实验中编写了一个模拟任务执行的控制台程序，分为Client端和Server端，用户通过Client端发送执行命令及数据，各异构处理器运行Server端接收指令和数据并执行。收发程序的具体执行过程如下。

1) 保持用户PC与拟态处理器系统联通。

2) 用户使用Client端程序向拟态处理器发送执行指令，由FPGA下达至各CPU的Server端；

3) 各CPU在收到指令和数据后进行处理，而后将结果上传。

4) FGPA记录任务的开始时间和结束时间。

5) FPGA对各CPU的输出进行仲裁，然后将最终结果上传给用户，Client端显示文件接收结果。

Server端每发一个数据，视为执行一次任务，任务执行周期由发包时间和处理时间组合得到。一次任务执行完后，间隔100 μs，Client端再发送一个执行指令。

4 实验仿真与分析

4.1 参数测定及分析

1) 最优放大系数选取过程

EPET算法考虑到实际网络环境中存在测量误差、传输处理时延等不可控因素，需要对算法预测得出的超时阈值进行合理放大，避免由于超时阈值过于贴近理论值而导致误报率升高。但放大系数的选取需依照不同系统环境来设定，一方面，若放大系数选取过小，难以解决误报率高的问题；另一方面，若放大系数选取过大，不仅可能导致异常执行体被判决为正常，也将增加正常执行体的平均等待时间，降低系统运行效率。

本文实验通过设置测试指令集，对放大系数取值范围在(1,2]内的执行体平均超时误报率及正常执行体平均等待时间进行测定，精度为0.1。其中，误报率定义为正常执行事件被判决为超时的次数占总执行事件的比率，正常执行体平均等待时间t定义为所有正常执行体对于同一任务的预测超时阈值与实际执行时间的差值平均值。实验结果如图2所示，从图2(a)中可以看出，在本文实验环境下，当放大系数小于1.6时，执行体平均超时误报率呈不断下降趋势，当放大系数大于1.6时，执行体平均超时误报率虽继续下降，但趋势放缓；从图2(b)中可以看出，预测超时阈值与实际执行时间的差值平均值不断增大。综上考虑，本文中放大系数选取为1.6。

图2 放大系数对EPET算法性能的影响

2) 最优执行体历史事件执行时间队列长度选择过程

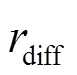
从图3所示实验结果可以看出，随着执行体历史事件执行时间队列长度的增加，差值比率的数值不断下降，表明超时阈值的预测准确率逐渐增大。但当队列长度超过5时，差值比率的数值下降速度放缓，继续增加队列长度不仅无法获得更加显著的性能提升，而且会继续增加系统存储开销，因此本文实验中选取队列长度为5。

图3 历史事件时间队列长度对EPET算法性能的影响

4.2 实验验证及分析

基于4.1节选取出的EPET算法最优参数，本节通过设定指令集对算法的有效性进行验证，实验结果如图4所示。从图4中的不同曲线不难看出，CPU在面对不同系统指令时的处理时间起伏较大，表明CPU在一段时间内任务量存在波动情况。在这种情形下，超时阈值能够及时随着CPU处理时间的变化而增加或减小，能够很好地适应任务量的剧烈和大幅变化。

图4 EPET算法部分实验结果及性能指标

从图4(a)可看出，4个执行体对连续多个任务的处理时间从20 μs到190 μs，如果采用固定阈值方法将超时阈值设置为固定值，则超时阈值需大于190 μs才能保证系统正常运行而不出现误报。为了保证一定的安全余量，超时阈值可能需要设置到250 μs甚至300 μs以上。且这是对所有任务而言的，即使执行体面临简单任务时的执行时间仅为20 μs，执行体也要等到所设置的固定阈值时刻才能够进行超时判断，将极大地降低整个处理系统的效率。

从图4(b)可知，按照本文提出的EPET算法预测出的超时阈值，可根据CPU任务量的变化自适应地升高或降低，阈值范围从不到30 μs至240 μs。当任务量较小时，超时阈值也较低，能够及时判断执行体的状态，节约执行体等待时间，提升处理系统效率；当任务量较大时，超时阈值也相应升高，能够有效降低虚警率。

从图4(c)可知，当CPU处于正常状态时，其超时阈值与实际执行时间的差值始终为正值，说明没有出现估算的超时阈值小于实际执行时间的情况，即EPET算法对于各CPU正常执行系统指令时的超时阈值预测未出现误报，且在合理范围之内。

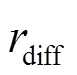
为进一步说明本文提出的EPET算法的有效性，取上述4种CPU上各指令执行时间平均值与固定阈值情况与文献[5]提出的滑动窗口预测算法STW进行性能对比，实验结果如图5所示。由于固定阈值的设置通常根据经验进行，因此针对本文实验环境，结合图4中的实验数据，可知系统的最大执行时间约为180 μs，为了保证一定的余量，对比实验中固定阈值设置为200 μs。

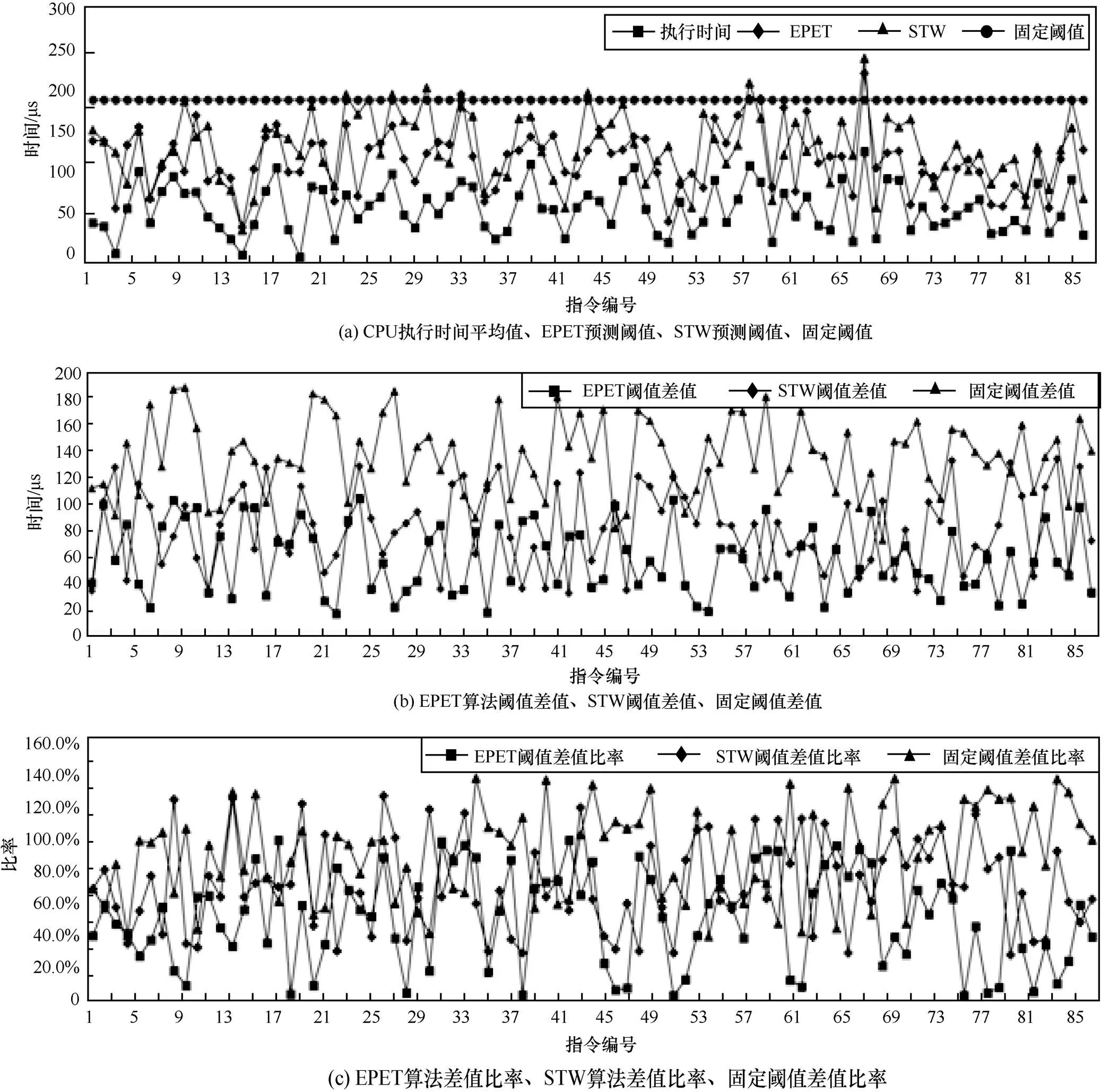
图5 固定阈值、PEPT算法超时阈值、STW算法超时阈值性能比较

图5(a)表示CPU对于系统指令的实际执行时间平均值与阈值（包括固定阈值，根据EPET算法计算得到的动态阈值，根据STW算法计算得到的动态阈值）；图5(b)表示不同阈值与实际执行时间的差值，包括EPET及STW动态阈值与执行时间的差，以及固定阈值与执行时间的差；图5(c)表示CPU在处理过程中差值相对执行时间的占比，即差值比率。从图中可以看出，当CPU在执行较为简单的任务时，一旦发生超时，在固定阈值条件下，需等待较长的时长甚至几倍于执行时间的时长才能够判断超时，造成整个系统长时间停滞，带来了不必要的时间浪费，影响指令执行效率。

在本例中，固定阈值条件下，超时阈值恒定为200 μs，超时阈值与系统实际执行时间的最大差值为180.2 μs，最小差值为93.9 μs，平均差值为136.5 μs；文献[5]中提出的STW算法超时阈值最大值为248.9 μs，最小值为79.5 μs，平均值为146.1 μs。而采用本文提出的EPET自适应计算超时阈值，超时阈值的最大值为224.3 μs，最小值为56.8 μs，平均值为124.8 μs，相对于200 μs的固定阈值减少了37.6%，相比于STW算法预测出的阈值减少了14.6%。这表明相同情况下，EPET算法相比固定阈值算法平均可节约37.6%的等待时间，且相比STW动态阈值预测算法缩短了14.6%的等待时间。进一步，STW算法超时阈值与系统实际执行时间的最大差值为131.9 μs，最小差值为47.5 μs，平均差值为98.8 μs；EPET算法预测出的超时阈值与系统执行时间的最大差值为103.4 μs，最小差值为24.7 μs，平均差值为76.1 μs。相对于固定超时算法，EPET超时阈值与系统执行时间的最大差值减少了51.3%，最小差值减少了56.5%，平均差值减少了39.1%；相比STW动态阈值预测算法，EPET超时阈值与系统执行时间的最大差值减少了21.6%，最小差值减少了48.1%，平均差值减少了22.9%。且在差值比率指数方面，EPET算法平均差值比率处于3种算法中最小值，表明本文的EPET算法具有最优的预测精度。

综合上述分析可知，本文提出的EPET算法可以根据系统指令执行时间的长短动态地改变超时阈值，在保证最大限度检测出系统异常的情况下，有效减少了等待时间，提高了超时识别的速度，避免了系统由于需要判断CPU是否正常而长时间等待的情况，尤其是针对某段时间内系统任务量波动较大的情况，EPET算法能够提供一个更为有效和灵活的方案。

5 结束语

本文提出了一种面向多执行体的自适应超时阈值预测算法EPET，该算法基于拟态防御架构中包含多个性能接近的异构功能等价体的特性，通过对每个执行体维护一个历史事件执行时间队列，采用等效比例执行时间策略得到当前任务的超时阈值。实验结果表明，相比固定阈值及动态阈值算法，本文提出的EPET自适应阈值预测算法可显著减少系统对CPU的超时判决速度，降低正常执行体平均等待时间，提升系统的整体运行效率，尤其适合执行体前后任务计算量无规律、波动较大的情况，具有低复杂度的特性。

[1] 邬江兴. 拟态计算与拟态安全防御的原意和愿景[J]. 电信科学, 2014, 30(7): 1-7.

WU J X. Meaning and vision of mimic computing and mimic security defense[J]. Telecommunications Science, 2014, 30(7): 1-7.

[2] 仝青, 张铮, 邬江兴. 基于软硬件多样性的主动防御技术[J]. 信息安全学报, 2017, 2(1): 1-12.

TONG Q, ZHANG Z, WU J X. the active defense technology based on the software/hardware diversity[J]. Journal of Cyber Security, 2017, 2 (1):1-12.

[3] 魏帅, 于洪, 顾泽宇, 等. 面向工控领域的拟态安全处理机架构[J]. 信息安全学报, 2017, 2(1): :54-73.

WEI S, YU H, GU Z Y, et al. Architecture of mimic security processor for industry control system[J]. Journal of Cyber Security, 2017, 2 (1):1-12.

[4] RYU B, CHENEY D, BRAUN H W. Internet flow characterization: adaptive timeout strategy and statistical modeling[C]// Passive & Active Measurement Workshop. 2001: 45.

[5] 钱迎进, 肖侬, 金士尧. 大规模集群中一种自适应可扩展的RPC超时机制[J]. 软件学报, 2010, 21(12): 3199-3210.

QIAN Y J, XIAO N, JIN S Y. Adaptive scalable rpc timeout mechanism for large scale clusters[J]. Journal of Software, 2010, 21(12): 3199-3210.

[6] 周明中, 龚俭, 丁伟. 网络流超时策略研究[J]. 通信学报, 2005, 26(4): 88-93.

ZHOU M Z, GONG J, DING W. Study of network flow timeout strategy[J]. Journal of Communications, 2005, 26(4):88-93.

[7] CLAFFY K C, BRAUN H W, POLYZOS G C. A parameterizable methodology for Internet traffic flow profiling[J]. IEEE Journal on Selected Areas in Communications, 1995, 13(8): 1481-1494.

[8] FONTI L, LUPINI F, MANGANELLI P. Timeout value adaptation: U S Patent 9,769,022[P]. 2017-9-19.

[9] 侯颖, 黄海, 兰巨龙, 等. 基于自适应超时计数布鲁姆过滤器的流量测量算法[J]. 电子与信息学报, 2015, 37(4):887-893.

HOU Y, HUANG H, LAN J L, et al. An adaptive timeout counter bloom filter algorithm for traffic measurement[J]. Journal of Electronics & Information Technology, 2015, 37(4):887-893.

[10] 余莹, 李肯立, 徐雨明. 计算集群中一种基于任务运行时间的组合预测方案[J]. 计算机应用, 2015, 35(8):2153-2157.

YU Y, LI K L, XU Y M. combined prediction scheme for runtime of tasks in computing cluster[J]. Journal of Computer Applications, 2015, 37(4):887-893.

[11] 张霄宏, 海林鹏, 贾宗璞, 等. 同构Hadoop环境作业执行时间计算方法[J]. 计算机工程与应用, 2014, 50(10):249-252.

ZHANG X H, HAI L P, JIA Z P, et al. Method for computing execution time of jobs in homogeneous Hadoop environments[J]. Computer Engineering and Applications, 2014, 50(10): 249-252.

[12] 张曹哲, 尤政. 超时策略动态阈值的阈值选择影响因素[J]. 哈尔滨工业大学学报, 2013, 45(6):119-123.

ZHANG C Z, YOU Z. The influencing factor of threshold selection in dynamic threshold of timeout policies[J]. Journal of Harbin Institute of Technology, 2013, 45(6):119-123.

Timeout threshold estimation algorithm in mimic multiple executors architecture

NIE Delei1, ZHAO bo2, WANG Chong2, WANG Xin3, YAN Binghao2

1. Economic-Technological Development Committee in Tianjin Binhai New Area, Tianjin 300000, China. 2. National Digital Switching System Engineering & Technological R & D Center, Zhengzhou 450002; China 3.Information Technology Innovation Center of Tianjin Binhai New Area, Tianjin 300000, China

Aiming at the problem that the current timeout strategy algorithm is difficult to cope with the violent situation of task volume, a timeout threshold prediction algorithm based on equivalent proportional execution time applied to the mimetic defense architecture system is proposed. The algorithm utilizes the principle that the execution time of multiple functional equivalent executable tasks in the mimetic defense architecture is positively related, predicts the task execution time and sets a reasonable timeout threshold. The simulation results show that the proposed algorithm can dynamically predict and set the timeout threshold for different task situations, which effectively improves the timeout judgment efficiency, especially for scenarios with dramatic changes in workload.

mimic defense, threshold calculation, multiple executors, timeout judgment

TP302.1

10.11959/j.issn.2096-109x.2018084

聂德雷（1988-），男，山东莒南人，硕士，天津市滨海新区科技和工业创新委员会主任科员，主要研究方向为网络安全。