一种基于进化的自适应卡尔曼修正粒子群优化算法

侯 森 李才发

（1.中国人民解放军信息工程大学，河南 郑州450002；2.中国人民解放军75842部队，广东 广州510880）

1.引言

粒 子 群 优 化 算 法 （Particle Swarm Optimization，PSO）是一种基于群体智能理论的全局优化算法，粒子群中的粒子代表着优化问题的可能解，每个粒子根据它自身存储的历史最优点和它邻居粒子记录的历史最优点来调整自己的运动速率和方向“飞”向全局最优解[1，2]。近年来，国内外学者进行了大量的粒子群优化算法相关研究，这些研究工作主要集中在两个方向上：一是改进粒子速率的更新方式，从而提高算法的收敛速度或者保持粒子群的多样性。如文献[3]中引入了惯性权重，文献[4]中提出了基于动态速率的算法。二是研究不同的样本，选择学习策略，从而使粒子能够快速收敛到接近最优解的区域内。这一类典型的方法包括广义自适应粒子群法[5]，基于异构分簇的粒子群优化算法[6]等。

大量的研究工作极大地丰富了粒子群算法的应用领域。但是这些研究工作大都是专注于提升粒子群算法某一方面的性能，目前仍然缺乏能够在各个领域普遍适用的算法。此外，粒子群算法因其可能出现早熟收敛,所以容易陷入局部最优点。改进PSO的关键在于如何选择合适的收敛速度，过快的收敛速度容易导致算法陷入局部最优点，而过慢的收敛速度又将极大地影响算法的效率。

本文从种群粒子位置更新过程的相关性角度出发，提出了一种基于进化的自适应卡尔曼修正粒子群优化算法。该算法在每次迭代过程中根据卡尔曼滤波修正机制调整算法最优点的位置，提升算法在搜索空间中的搜索效率和收敛速度。同时作者使用了一种基于子梯度计算的方法自适应地调整算法的系数，从而提高算法的收敛率。此外，为了克服早熟收敛，作者采取了基于自然选择的达尔文进化机制，通过多个子群的自然进化，增强粒子群的多样性，从而使算法免于陷入局部最优点。

2.粒子群优化算法(PSO)

2.1 PSO的基本形式

每个粒子的速度和位置更新策略分别为：

2.2 改进PSO算法

由于算法的简洁和高效，PSO自被提出以来就受到了众多学者的关注和研究。近年来国内外学者提出了许多PSO改进算法，其中比较有代表性的研究有：Clerc and Kennedy引入了惯性权重ω来控制粒子的运动速率[3]，它通过前一状态速率的加权乘积来防止当前速率过度激增，并将速度更新公式改写成了如下形式：

惯性权重ω对于算法的收敛非常重要，惯性权重既可以是静态的，也可以采用动态的。在算法初期搜索阶段，粒子被赋予较大的速度有助于提高搜索效率加快收敛；在算法后期收敛阶段，粒子被赋予较小的速度则能够避免陷入局部最优点。文献[7]采取了一种非线性的惯性权重方式：

其中ω1和ω2分别代表惯性权重的初始值和最终值。惯性权重在初始阶段具有较大的值，随着迭代次数k的增加惯性权重快速减小，从而使得惯性权重在算法不同的阶段发挥不同的作用。公式（4）所定义的惯性权重能够较好地改善算法性能，但是这种形式的惯性权重并不能模拟所有优化问题的情况，例如对于多峰类型的优化函数，这种形式的惯性权重就不能很好地发挥作用。

3.基于进化的自适应卡尔曼修正粒子群算法

目前，绝大多数的PSO改进算法都是基于速度更新公式的改进，通过控制惯性权重或者加速系数等方式使得PSO算法在不同阶段具有不同的变化趋势，从而实现快速收敛和避免陷入局部极值点。然而基于位置更新公式的改进尚未有人尝试，位置更新公式同样提供给我们了许多信息，位置的变化趋势更多地体现了种群的相关特性，因而将有助于算法的快速收敛。本文提出了一种基于进化的自适应卡尔曼修正粒子群优化算法。该算法在每次迭代过程中根据卡尔曼滤波修正机制调整算法最优点的位置，这样的调整能够显著地提升算法在搜索空间中的搜索效率和收敛速度。同时作者使用了一种基于子梯度计算的方法来自适应地调整算法的系数，以此来实现提高算法收敛率。此外，为了克服早熟收敛，作者采取了基于自然选择的达尔文进化机制，通过多个子群的自然进化，避免使算法陷入局部极值点。

3.1 卡尔曼修正机制(Kalman Correction)

粒子群算法在对种群中每个粒子的位置进行迭代更新后，会计算它们的适应度，然后通过适应度的数值判断粒子的优劣。如果粒子当前位置的适应度好于历史全局最优点，则新的位置代替原来的全局最优点。这种简单比较的方式虽然有效，但是并没有充分考虑到全局最优点更新过程中的相关性。由于群体智能的社会认知特性，粒子群在向全局最优点收敛过程中的运动并不是随机的，因而我们可以利用其中的相关性来修正粒子群全局最优点的更新过程。

本文采用一种类似非线性滤波的卡尔曼修正机制 (Kalman Correction)在每次位置更新后对全局最优点进行调整，从而提高算法搜索效率。假设粒子群的适应度函数为。第k次迭代后，粒子i在位置的适应度值如下：

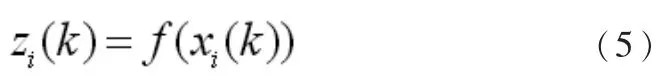
经过k次迭代后，粒子群中当前位置适应度最优的点为xg，历史全局最优点位置为pg。我们定义两者之间的估算误差为。

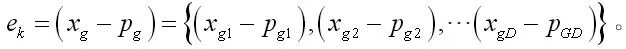
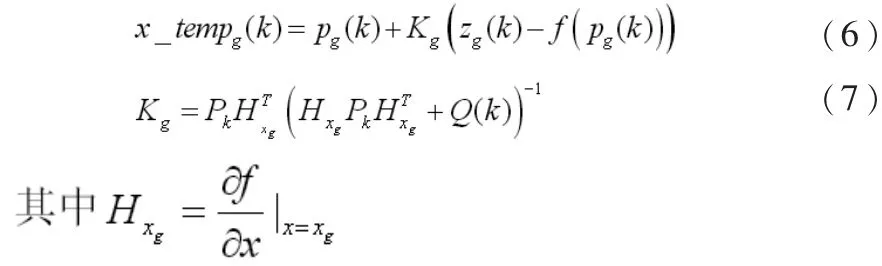
通过上式所示卡尔曼修正机制，算法可以根据全局最优点的历次更新，拟合出近似最优点的非线性更新轨迹。最优点适应度的观察噪声为零，而最优点的激励噪声可以看做是零均值的协方差为Q的高斯白噪声。假设我们给定噪声协方差初始值，根据Sage-Husa自适应算法[8]，噪声统计特性的更新方程为：

其中d为权重系数。

我们在每次迭代后计算出修正的当前最优点，然后同种群历史全局最优点进行适应度的比较，如果修正后的当前最优点x_tempg(k)优于历史全局最优点 pg(k)，则用 x_tempg(k)代替 pg(k)。

3.2 基于子梯度的自适应系数更新

虽然卡尔曼修正机制能够有效地提升算法在解空间中的搜索速度，但是算法仍会受到惯性权重ω和加速系数的制约。根据PSO算法的原理，当初始化阶段算法从远离全局最优点的任意位置开始搜索时，如果我们能够给予粒子较大的速度则有利于算法快速收敛；当粒子群逐渐汇聚到最优点附近区域时，如果我们适度降低粒子的速度，则能够避免粒子跳过最优点，提高算法收敛率。因而我们考虑根据粒子到最优点距离的不同，自适应地调整算法的相关系数，赋予粒子不同的搜索速度，这样将有效地提高我们算法的准确性和收敛率。本文设计了一种基于子梯度的自适应系数更新方案，根据粒子到最优点的距离动态地更新算法系数。

惯性权重ω以及加速系数c1、c2对PSO算法的性能非常重要，根据粒子到最优点距离的不同我们可以赋予粒子不同的参数。当粒子远离全局最优点时，我们可以设置较大的参数，提高运动速度从而加快收敛；当粒子越来越靠近全局最优点的时候，我们可以选择较小的参数，避免算法在最优点附近震荡，跳过最优点。假设粒子i与全局最优点的距离为Dig，优化的目标是选取合适的参数使得此距离最小。

受子梯度方法的启发，我们用下列形式更新惯性权重ω以及加速系数c1、c2：

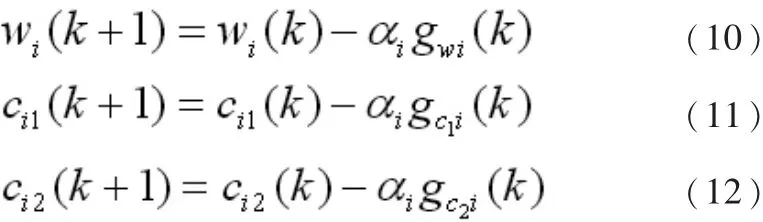
其中 αi是步幅，gwi(k)、gc1i(k)、gc2i(k)分别是惯性权重ω以及加速系数c1、c2在公式(8)中的子梯度。

根据Polyak步幅方程，步幅αi可以写作：

通过公式(10)～(16)，我们可以根据粒子到最优点的距离自适应地调整粒子的参数。

3.3 基于自然选择的达尔文进化过程

通过采取上述卡尔曼修正和子梯度系数更新机制，虽然我们可以提高粒子群算法的搜索速度和收敛效率，但是算法仍然容易陷入局部最优点。正如硬币的双面一样，快速收敛和避免陷入局部最优点是粒子群算法固有的悖论。提高搜索速度难免增加早熟收敛的可能性，已有的许多算法通过增加粒子群多样性来调和两者之间的矛盾。受文献[7]的启发，我们采取基于自然选择的达尔文进化机制提高算法的全局搜索能力。

首先，我们将整个粒子群划分为无数个动态子群，各子群通过独立地繁殖、选择和淘汰等自然操作，逐步向全局最优进化，通过搜索多样性，能够有效地避免陷入局部极值点。子群可以动态的增长或者消亡。一个子群可以找到更好的适应度值从而延长寿命，同时也可以增加新的粒子来加快搜索速度；在连续若干迭代步骤中，如果一个子群没有得到更优的适应度值，那么将缩短它的寿命，并且删除子群中性能较差的粒子，当子群中的粒子数量减少到一定阈值时，该子群将被销毁。

达尔文进化机制为每个粒子群中设置一个搜索计数器SC，记录适应度值没有变化的次数，如果SC超过最大门限SCcmax，则删掉适应度值最差的粒子。初始SC设置为0，每次删除粒子后，SC值不复位，而是按照公式（17）重新设置。

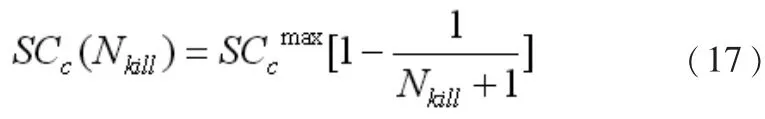
3.4 基于达尔文进化的自适应卡尔曼修正粒子群算法

综上所述，AKDPSO算法的实现步骤可概括如下。

（1）输入：粒子群，粒子数N及空间维数D。

（2）输出：全局最优点pg与最佳适应度值。

（3）初始化：设定最大迭代代数tmax搜索计数器最大门限SCcmax，粒子的初始位置xi(0)和初始速度pi(0)，粒子群初始最优位置pg(0)，初始惯性权重 ω(0)以及加速系数 c1(0)、c2(0)。

（4）划分若干初始子群，估计每个粒子的适应度，设置粒子当前位置为其极值pi(0)，设置初始全局最佳粒子的位置为全局极值pg(0)。

（5）Repeat

for每个粒子群 do

for每个粒子 do

①根据式(13)-(15)更新系数子梯度：

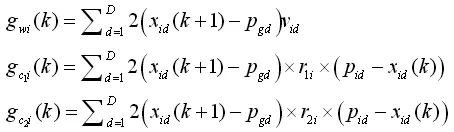
根据式(10)-(12)自适应更新惯性权重ω和加速系数：

②应用式(2)与(3)实现粒子位置与速度的更新

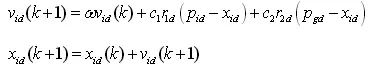
③对状态更新后的粒子适应度值进行评估，如果优于当前的自身最优值，则将pi(k)设置为该粒子的位置，并且更新自身最优值。

end for

④如果存在粒子的最优值好于当前全局最优值，则将pg(k)设置为该粒子的位置，且更新全局最优点。

⑤根据式(6)-(8)定义的卡尔曼修正机制调整全局最优点的位置

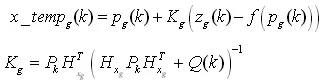
如果修正的最优点适应度好于当前记录的全局最优值，则用修正值更新全局最优点。

⑥if粒子群的全局最优点得到了改进 do

奖励粒子群：增加粒子；延长粒子群寿命

endif

elseif do

惩罚粒子群：缩短粒子群寿命；删除计数器SC超过SCcmax的粒子。

endif end for

for每个粒子群 do

⑦如果粒子群寿命或者粒子群中粒子数量少于门限，删除该粒子群，按照式(17)重置搜索计数器。

⑧如果粒子群中没有粒子被删除，并且粒子群数量不超过其最大数目N，则按概率衍生后代，产生新的子群。

end for

until当达到最大迭代次数或者整个粒子群适应度不再发生显著变化，停止迭代。

return全局最优点pg与最佳适应度值。

上述算法能够有效提高搜索速度和收敛率，同时继承了达尔文进化的优点，降低了粒子群陷入局部极值的可能。

4.实验与分析

4.1 测试函数与算法配置

我们选取了六个典型函数来测试AK-DPSO算法的性能，它们的表达式如下表所示。

表1 六个典型函数

其中f*为全局极值。同时我们选取PSO、HPSO、DPSO、APSO、FO-PSO 五种算法与本文提出的AK-DPSO算法进行比较，将上述6个函数表达式作为适应度函数。各PSO算法的初始参数设置如表2所示，其中粒子数N=50，空间维数D为20，最大迭代次数 tmax=1000。

表2 各PSO算法的参数设置

4.2 搜索精度比较

为了减少统计误差，对每个函数进行了30次测试，然后取其平均值进行比较。通过表3可以看出，无论是在单峰函数 f1、f2、f3上，还是在多峰函数f4、f5、f6上，基于进化的自适应卡尔曼修正粒子群优化算法的测试结果均要好于现有的PSO及其优化算法。

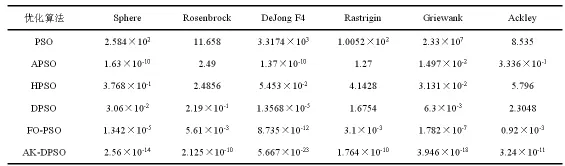
表3 不同粒子群优化算法对6个测试函数的搜索结果比较

4.3 算法稳定性能比较

我们用最优解方差函数来评价算法的稳定性，定义如下：

当∣fi-favg∣＞1 时，fmax取值为 max(∣fi-favg∣)，否则取1。如表4所示，AK-DPSO算法的最优值方差小于其他五种算法，因此AK-DPSO算法搜索到的最优解最稳定。

表4 测试函数的最优值方差比较

4.4 收敛速度比较

图 1(a)～(f)为 APSO、HPSO、DPSO 与本文提出AK-DPSO算法对典型测试函数优化过程中，种群收敛性能的对比。图1中的纵坐标表示适应度的对数值，横坐标为迭代次数。

通过上图可以看出，本文提出的AK-DPSO算法比APSO、HPSO和DPSO算法收敛速度更快，并且能够跳出局部最优值，从而提升了算法的全局搜索能力，有效地避免了早熟收敛问题。

综上所述，与现有的几种PSO算法相比较，AK-DPSO算法收敛速度、稳定性以及搜索精度都得到了明显提高，展示出更令人满意的整体优化性能。

4.5 算法的计算复杂度分析

作者对比了AK-DPSO算法和上文五种对比算法在1000次迭代次数内对上文六个函数的平均计算时间，以比较几种算法的复杂度。同时作者还比较了粒子群规模与算法复杂度的关系，实验结果如图2所示。

AK-DPSO算法复杂度略高于其他算法，其主要原因是AK-DPSO算法由于使用了粒子的位置和速度参数进行动态调整，粒子每次迭代都将增加O(2(N-1)D+N)的计算复杂度。AK-DPSO增加了计算复杂度，但是获得了较高的搜索精度、较快的收敛速度和较好的稳定性。

5.结论

为了避免陷入局部极值点和快速收敛，本文从种群粒子位置更新过程的相关性角度出发，提出了一种基于进化的自适应卡尔曼修正粒子群优化算法，在此基础上给出了AK-DPSO算法。该算法在每次迭代过程中根据卡尔曼滤波修正机制调整算法最优点的位置，提升算法在搜索空间中的搜索效率和收敛速度；同时作者使用了一种基于子梯度计算方法自适应地调整算法的系数，采取了基于自然选择的达尔文进化机制，避免使算法陷入局部极值点。相比于现有的主要粒子群优化算法，本文的AK-DPSO算法的搜索精度、收敛速度和稳定性都有了显著提高，全局寻优能力得到了极大提升。