基于双变量单向函数的门限可变秘密共享方案

黄科华，陈和风



基于双变量单向函数的门限可变秘密共享方案

黄科华1，陈和风2

（1. 泉州幼儿师范高等专科学校 初等教育系，福建 泉州 362000；2. 集美大学 计算机工程学院，福建 厦门 361021）

利用双变量单向函数和拉格朗日插值公式构造了一个门限秘密共享方案，该方案可以按照事先预定的门限来进行秘密共享（门限可变），不需要使用到安全信道，用户的份额不会暴露，可以多次使用，是一个完美的秘密共享方案。

门限可变秘密共享方案；双变量函数；拉格朗日插值公式

1 研究背景

为安全起见，银行保险柜的钥匙不能由一个人单独保存，必须由多个人，每个人掌握一部分钥匙。当足够多的人集中在一起的时候，才能打开保险柜。解决类似问题的方案我们称之为秘密共享方案（，）。一个秘密共享方案由以下几个部分组成：：可信中心或者密钥分发者：合成密钥参与者集合、密钥集合、准入结构（由可合成密钥的集合组成）、分配算法和合成算法。

(,)门限秘密共享方案是比较流行的秘密共享方案，它指的是个参与者中，个或者大于个成员合作可以合成密钥，而少于个人合作得不到密钥的任何信息的秘密共享方案。Shamir和Blakley于1979年分别独立提出了基于拉格朗日插值公式和线性集合投影方法的(,)门限秘密共享方案[1,2]。此后有一些研究者对方案进行了改进[3-6]。这些方案都存在着一些不足之处，如：（1）需要使用到安全信道来传输密钥份额；（2）份额只能使用一次，如果要合成新密钥，还需重新再次发送份额；（3）准入结构较为单一，确定完就无法改变等。针对这些不足，有的研究者提出了多秘密共享方案[7-8]、可验证秘密共享方案[9]、加权秘密共享方案等[10]。

在解密之前，有可能需要对门限值进行改变，如系统安全等级升高或者下降、成员的份额泄露或者信任度降低等。Laih等人于1989年首次提出了门限可变秘密共享概念并给出了相应方案[11]。此后，一些研究者陆续利用插值公式[12]、基于格等技术[13]，构造门限可变秘密共享方案。本文在这些方案的基础上，提出了一个基于双变量单向函数的门限可变秘密共享方案。

2 预备知识

2.1 陷门单向函数

陷门单向函数可以选择RSA函数等。

2.2 双变量单向函数

函数(,)称为双变量单向函数，其满足以下条件：

（1）对于确定的,，可容易计算=(,)；

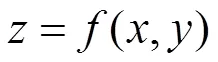
文献[14]证明了双变量单向函数的存在，并在()（为大素数）上提供了一种利用一对一hash函数的构造方法。

2.3 完美秘密共享方案

3 基于双变量单向函数的门限可变秘密共享方案

以下方案皆在()（为大素数）上进行讨论。假设密钥分发者要把个密钥

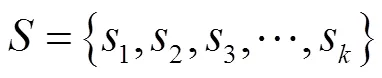
分享给个成员

3.1 密钥的分发阶段

（5）分发者选择个多项式

3.2 密钥的合成阶段

4 对本方案的分析

4.1 门限可变

4.2 不需要安全信道

4.3 成员的私钥可以重复利用

4.4 该方案是一个完美的秘密共享方案

5 结语

引入双变量单向函数构造了一个可变门限的秘密共享方案，该方案可以按照事先预定门限来进行秘密共享（门限可变）；不需要使用到安全信道；密钥合成后，用户份额不会暴露，可以多次使用；该方案是一个完美秘密共享方案。

[1] Shamir A. How to share a secret[J]. Communications of the ACM, 1979, (11): 612-613.

[2] Blakley G R. Safeguarding cryptographic keys[A]. Proceedings of the National Computer Conference[C]. US: American Federation of Information Procession Societies, 1979: 242-268.

[3] Asmuth C, Bloom J. A modular approach to key safeguarding[J]. IEEE Transactions on Information Theory, 1983, (2): 208-210.

[4] Mignotte M. How to share a secret[A]. Proceedings of the Workshop on Crytography[C]. Burg Feuerstein, Germany, 1983: 371-375.

[5] Karnin E, Greene J, Hellman M. On secret sharing systems[J]. IEEE Transactions on Information Theory, 1983, 29(1): 35-41.

[6] Brickell E F, Davenport D M. On the classification of ideal secret sharing schemes[J]. Journal of Cryptology, 1991, (2): 123-134.

[7] He J, Dawson E. Multistage secret sharing based on one-way function[J]. Electronics Letters, 1994, 30(19): 1591-1592.

[8] Yang C, Chang T, Hwang M. A (t, n) multi-secret sharing scheme[J]. Applied Mathematics and Computation, 2004, 151(2): 483-490.

[9] Chor B, Goldwasser S, Micali S. Verifiable secret sharing and achieving simulataneity in the presence of faults[A]. 26th Annual Symposium on Foundations of Computer Science[C]. Portland, USA, 1985: 383-395.

[10] S Iftene, I Boureanu. Weighted threshold secret sharing based on the Chinese remainder theorem[J]. Scientific Annals of the “Al. I. Cuza” University of Iasi, Computer Science Section, 2005.

[11] Laih C-S, Harn L, Lee J-Y, et al. Dynamic threshold scheme based on the definition of cross-product in an n-dimensional linear space[J]. Journal of Information Science and Engineering, 1991, 7(1): 13-23.

[12] Zhifang Zhang, Yeow Meng Chee, San Ling, et al. Threshold changeable secret sharing schemes revisited [J]. Theoretical Computer Science, 2011: 418.

[13] Ron Steinfeld, Josef Pieprzyk, Huaxiong Wang. Lattice-based threshold-changeability for standard CRT secret-sharing schemes[J]. Finite Fields and Their Applications, 2005:12(4)35-36.

[14] He J, Dawsom E. Multisecret-sharing scheme based on one-way function[J]. Electronics Letters, 1995, 31(2): 93-95.

Threshold Changeable Secret Sharing Schemes Based on Two-Variable One-Way Function

HUANG Ke-hua1, CHEN He-feng2

(1. Department of Primary Education, Quanzhou Preschool Education College, Quanzhou362000, China; 2. Computer Engineering College, Jimei University, Xiamen361021, China)

By using two-variable one-way function and Lagrange interpolation formula, we create a perfect threshold secret sharing scheme which is able to share secret according to the set threshold (which means it’s changable) for many times, while not using secure channels or revealing users’ shares.

Threshold Changeable Secret Sharing Schemes; Two-variable One-way Function; Lagrange interpolation formula

O1-0

A

1009-9115(2018)06-0041-03

10.3969/j.issn.1009-9115.2018.06.009

福建省自然科学基金项目（2017J01761），厦门市科技局平台补助金项目（B16145）

2018-05-07

2018-09-21

黄科华（1983-），男，福建泉州人，硕士，副教授，研究方向为密码学、信息安全。

（责任编辑、校对：赵光峰）