地震作用下网架结构振动反应敏感区域的确定方法
2018-12-24时瑞国杨江波
时瑞国,杨江波,赵 莉
地震作用下网架结构振动反应敏感区域的确定方法
时瑞国1,杨江波1,赵 莉2
(1.邢台职业技术学院, 河北 邢台 054035;2.河北劳动关系职业学院,河北 石家庄 050002)
文章从多质点弹性体系的动力平衡方程出发,基于体系的位移反应计算公式提出了一种振型组合的计算公式,利用该公式可以求得组合振型图,进而确定网架结构振动反应的敏感区域,为快速确定网架结构中阻尼器的合理布置位置提供了理论依据。
网架结构;模态分析;振型参与系数;振型组合
一、概述
钢材作为一种绿色环保的建筑,凭借其强度高、自重轻、塑性好等优点在工程中得到了广泛应用。网架是钢结构中常用的一种结构形式,是由多根钢管和球节点通过焊接或螺栓连接的形式连接在一起形成的空间结构,其可以跨越很大的跨度,适用于体育馆、影剧院、候车厅等大型公共建筑的屋盖。网架结构抗震性较好,但在遭受强烈地震作用时,也会出现杆件变形、节点破坏的现象,严重时还有可能导致整体坍塌[1]。工程中为了提高网架的抗震性能,将消能减震技术应用到网架结构中,即在网架结构的适当位置设置阻尼器,依靠其强大的耗能能力衰减输入到结构中的能量,从而降低结构的地震反应。为了达到较好的减震效果,粘滞阻尼器应该设置在结构振动反应的敏感区域,而网架结构跨度大、杆件数目多,动力特性复杂,很难找到阻尼器的合理设置位置。本文基于振型组合的思想,提出一种确定网架结构振动反应敏感区域的方法,为快速寻找阻尼器的合理布置位置提供了依据。
二、网架结构振动反应敏感区域的确定方法
多质点弹性体系受到地震作用时,其动力平衡方程[2]为:
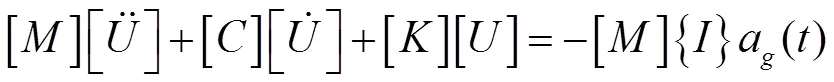
将位移向量用振型来表示,即
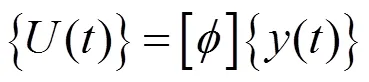
应用瑞利阻尼,阻尼矩阵可以写成质量矩阵和刚度矩阵的组合,即
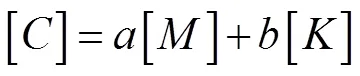
将(2)式、(3)式代入(1)式可得
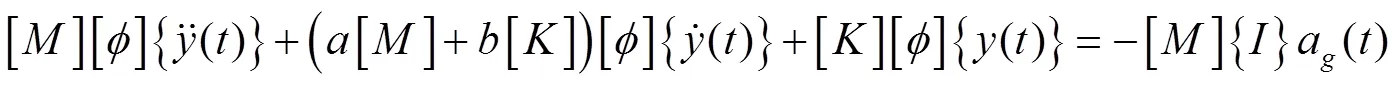
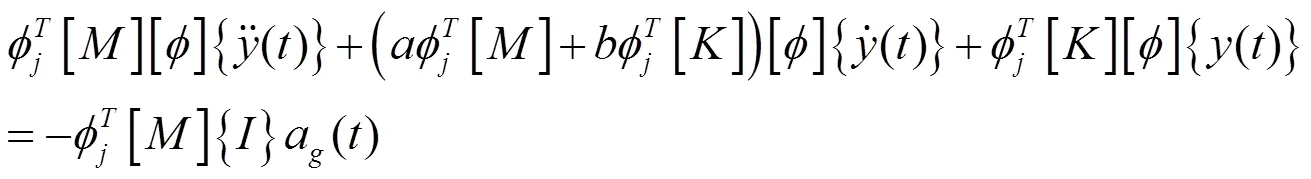
考虑到振型关于质量阵[M]、阻尼阵[C]和刚度阵[K]均满足正交条件[3],(5)式可以进一步写成
化简后得到
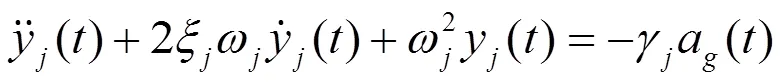

(9)式是一个常系数的二阶非齐次微分方程,方程的解由通解和特解两部分组成,其中通解部分表示自由振动的情况,在体系的阻尼作用下,这一部分会很快消减,分析时可以不考虑此部分的影响,只需求得其特解即可,根据杜哈梅积分求得其特解如下:
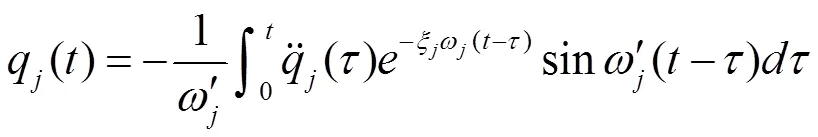
体系的位移反应可以写成[4]
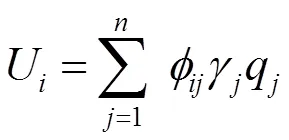
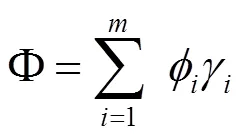
对结构体系进行模态分析,获得结构的动力响应参数,包括结构的振动形态、周期、频率及质量参与系数等,从而确定结构的主要振动方向,每个方向分别选取振型质量参与系数较大的振型进行组合,参与组合的振型个数应确保质量参与系数之和大于0.9[5]。将每个方向所选振型的节点相对位移与各自相应的振型参与系数相乘后代数相加,得到的代数和导入matlab软件即可绘制出每个主要振动方向的组合振型图,在图中可以直观、形象地看到振动的敏感区域。综合各个主要振动方向的组合振型图,即可确定阻尼器的合理布置位置。
三、计算案例
利用SAP2000软件建立一空间网架结构,形式及尺寸如图1所示。
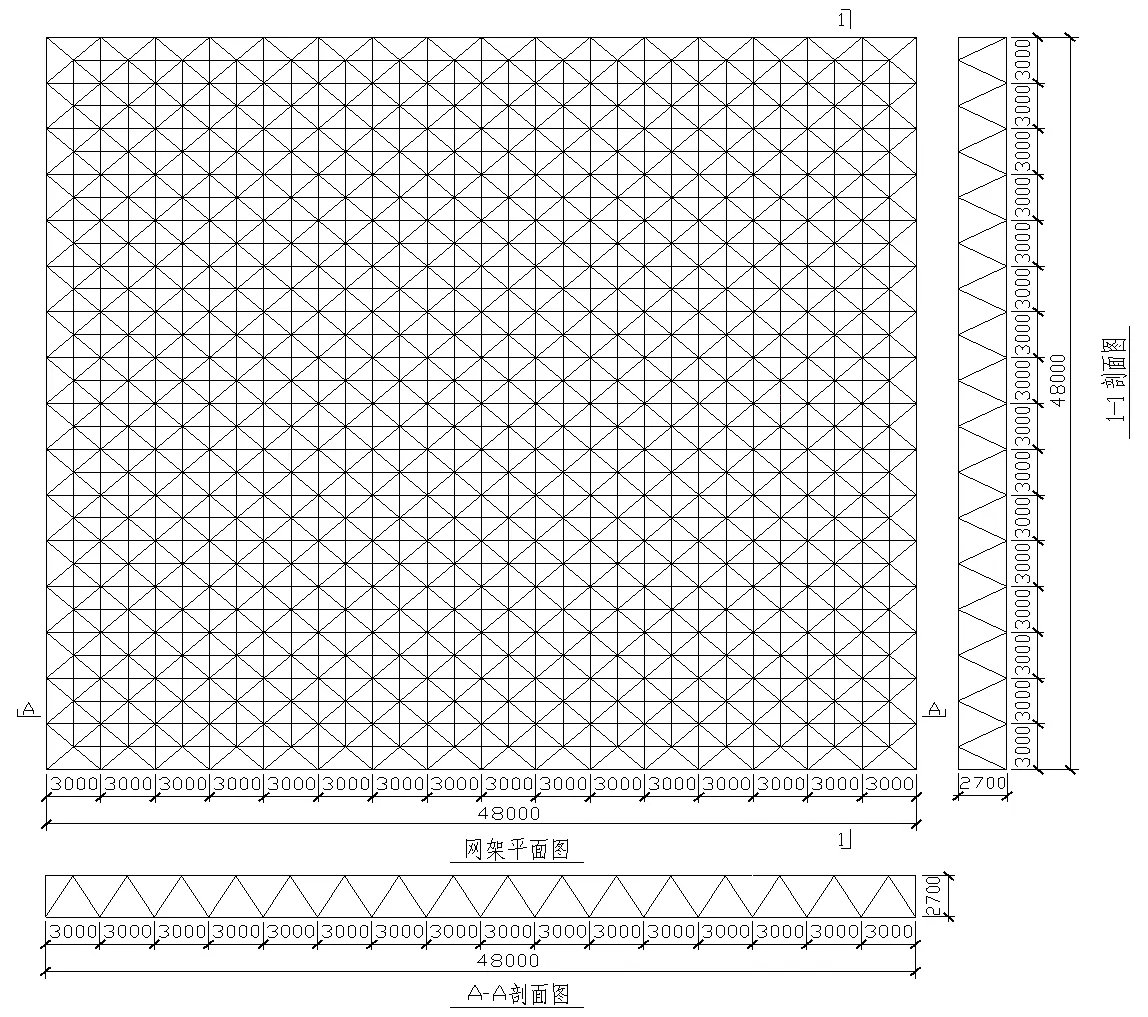
图1 空间网架平面图
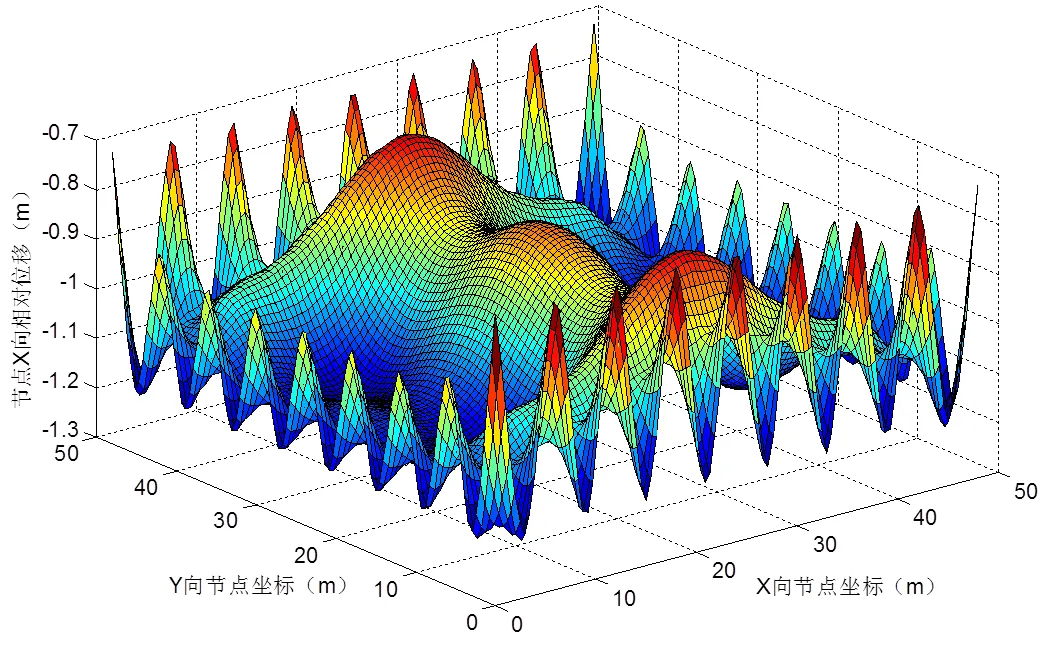
图2 水平方向组合振型图
模态分析表明地震作用时网架结构水平方向振动强烈,选取该方向振型质量参与系数较大的振型进行组合,得到的组合振型图如图2所示。
从图中可以看出网架周边图形坡度较大,为振动反应的敏感区域,在此区域布置20个阻尼器,具体布置位置如图3所示。
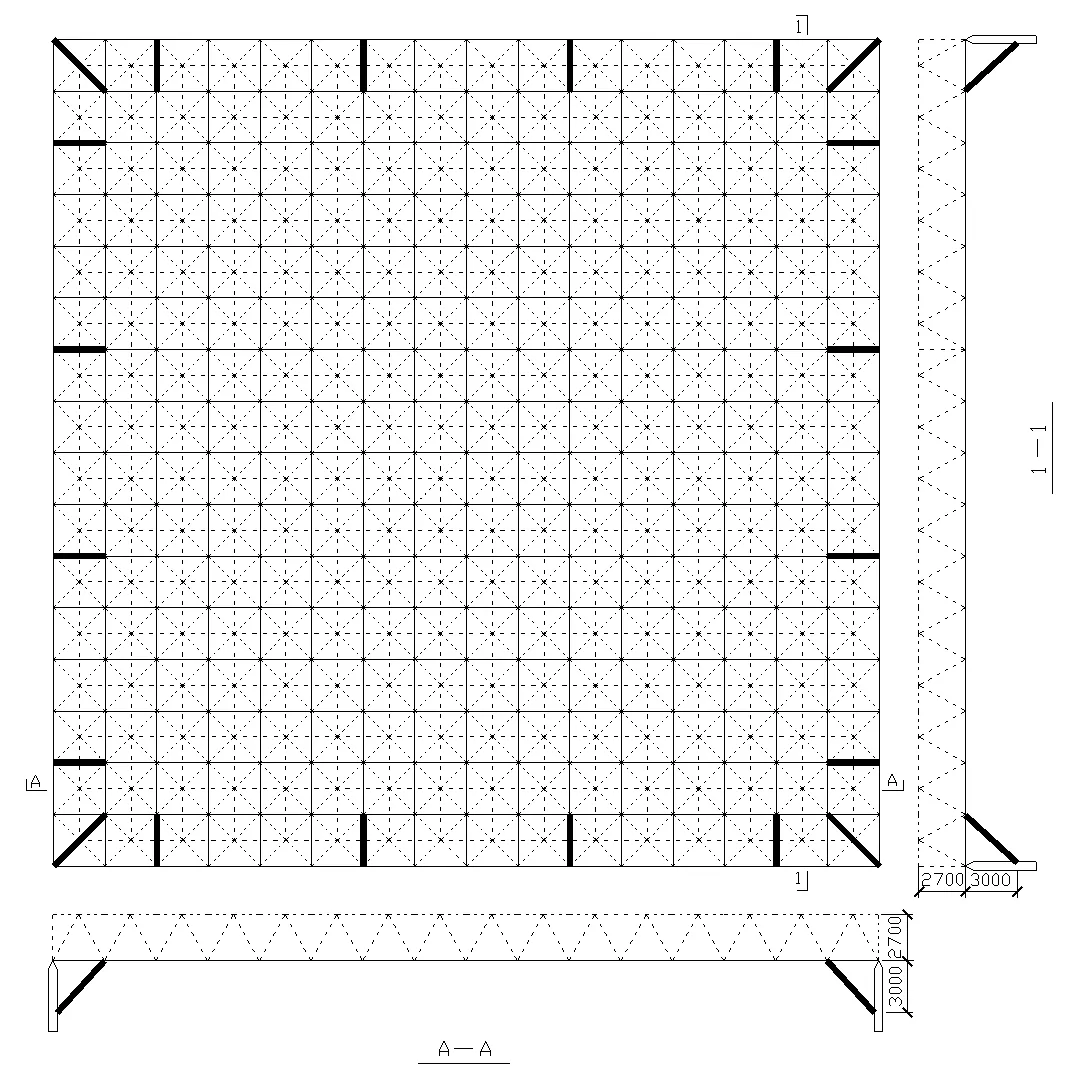
图3 阻尼器布置图
在三个方向输入地震波,对结构进行时程反应分析,分析结果表明在振动反应的敏感区域布置阻尼器可以取得较好的减震效果,控制节点和控制杆件的减震效果如下图4和图5所示。
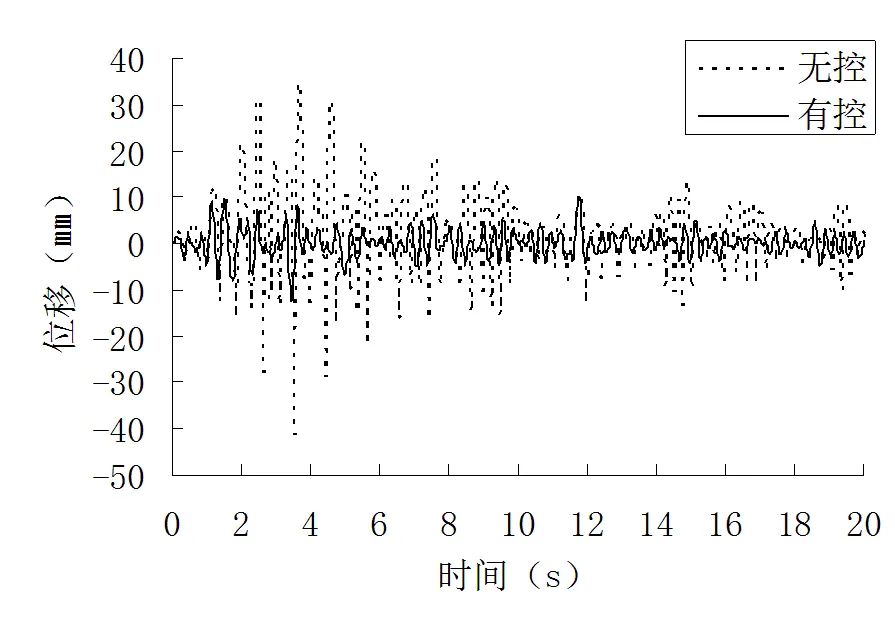
图4 控制节点Z向位移减震效果图
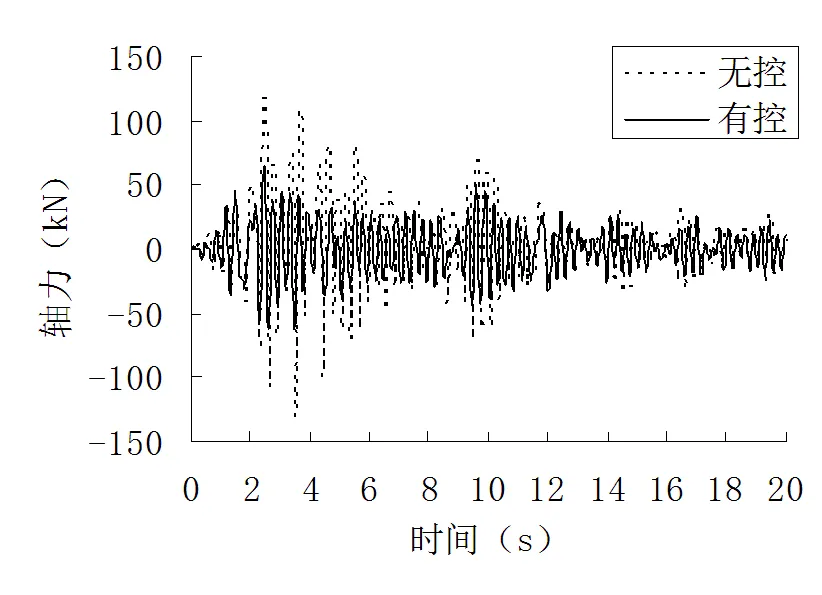
图5 控制杆件轴力减震效果图
四、结论
(1)本文从多质点弹性体系的动力平衡方程出发,基于体系的位移反应计算公式提出了一种振型组合的计算公式,根据这一公式可以求得组合振型。
(2)本文详细介绍了确定方法的实施步骤,按照实施步骤操作可以快速、准确地确定结构振动反应的敏感区域,进而确定阻尼器的合理布置位置,为工程的设计与施工提供了可靠的理论依据。
[1]张辰啸.空间双层网格结构强震失效机理与隔震研究[D].哈尔滨:中国地震局工程力学研究所,2016.
[2]刘习军,贾启芬.工程振动理论与测试技术[M].北京:高等教育出版社,2004.
[3]于建华,谢用九,魏泳涛. 高等结构动力学[M].四川:四川大学出版社,2001.
[4]郭继武.建筑抗震设计(第四版)[M].北京:中国建筑工业出版社,2017.
[5]孙广俊,李爱群.关于结构振型参与系数和振型贡献的分析[J].防灾减灾工程学报,2009,29(05):486-489.
The Method for Determining Vibration Sensitive Area of Grid Structure under Earthquake
SHI Rui-guo1,YANG Jiang-bo1,ZHAO Li2
(1.Xingtai Polytechnic College, Xingtai, Hebei 054035, China;2.Hebei Labor Relations Vocational College, Shijiazhuang, Hebei 050002, China)
In this paper, with reference to the dynamic equilibrium equation of multi-particle elastic system, a calculation formula of vibration mode combination is proposed based on the calculation formula of displacement response of the system. The formula could be used to obtain the combined vibration pattern and determine the the sensitive area of the vibration response of the grid structure. A theoretical basis is provided for quickly determining the reasonable arrangement position of the damper in the grid structure.
grid structure; modal analysis; mode participation coefficient; mode combination
2018—08—26
时瑞国(1987—),河北邢台人,邢台职业技术学院,讲师。
TU311
A
1008—6129(2018)05—0086—04
