A Filtering Approach Based on MMAE for a SINS/CNS Integrated Navigation System

Fangfang Zhao,Cuiqiao Chen,Wei He,Senior Member,IEEE,and Shuzhi Sam Ge,Fellow,IEEE

Abstract—This paper explores multiple model adaptive estimation(MMAE)method,and with it,proposes a novel filtering algorithm.The proposed algorithm is an improved Kalman filter—multiple model adaptive estimation unscented Kalman filter(MMAE-UKF)rather than conventional Kalman filter methods,like the extended Kalman filter(EKF)and the unscented Kalmanfilter(UKF).UKF is used as a subfilter to obtain the system state estimate in the MMAE method.Single model filter has poor adaptability with uncertain or unknown system parameters,which the improved filtering method can overcome.Meanwhile,this algorithm is used for integrated navigation system of strapdown inertial navigation system(SINS)and celestial navigation system(CNS)by a ballistic missile’s motion.The simulation results indicate that the proposed filtering algorithm has better navigation precision,can achieve optimal estimation of system state,and can be more flexible at the cost of increased computational burden.

I.INTRODUCTION

THE requirement for accuracy is high in this area of autonomous navigation,especially with rapid developments in information technology.However,obtaining the motion state of a ballistic missile with high precision is very difficult when using only a single navigation technology.Strap-down inertial navigation system(SINS)has attracted more and more attention from transportation department and the space shuttle,in view of a lot of significant advantages of strong autonomy,high accuracy,and low computational cost.However,the errors of SINS increase with time,hence for long durations,it is difficult to use SINS independently[1].Celestial navigation system(CNS)is also an autonomous navigation system where errors do not accumulate over time.Furthermore,CNS can provide the advantages of high location precision and good concealment.While it cannot independently accomplish positioning through navigation with the constraint of external conditions.Thus,there is a complementary relationship between SINS and CNS in terms of error characteristics,and we may increase the performance of navigation through their combination[2].No matter domestic or abroad,integrated navigation has been widely used with a series of advantages and obtained important achievements.For instance,utilizing each subsystem’s information can increase precision of the system positioning and raise the system reliability[3].Accordingly,SINS/CNS integrated navigation can be applied to the ballistic missile movement.

For this navigation system,filtering algorithm is a significant factor affecting navigation performance,which is frequently used to estimate state and filter measurement.In the information fusion,Kalman filter(KF)is a basic algorithm aiming at acquiring the attitude,velocity,and position information of the target.Improved filtering methods,such as EKF and UKF,have been developed based on the standard Kalman filter[4].

It is difficult to gain the optimal navigation estimation solely relying on KF due to the nonlinearity of the missile’s model,and both the EKF and UKF are suitable for nonlinear system[5].EKF works by utilizing a first-order Taylor series expansion to approximate linear system,then processing equations according to linear equations.However,linearization may cause the filter’s divergence and poor performance when the system has strong nonlinearity.Julier and Uhlman provide the theory of UKF,which effectively solves the problem related to EKF based on the assumption that the state variables’distribution approximates a Gaussian distribution[6],[7].Essentially,UKF adopts an unscented transformation(UT)strategy and provides a higher order moment of function without the need to linearize the nonlinear equations or compute the Jacobian matrix,as required in EKF.Therefore,UKF has no higherorder terms truncation error and can achieve higher precision compared with EKF for nonlinear system[8].Under the hypothesis that the process and measurement noise of EKF and UKF are a Gaussian distribution with zero-mean,we end up with the problem of filter tuning.This problem is timeconsuming and taxing.Fortunately,there are many available tools to aid the filter design.A popular approach to resolve this problem is to adopt an adaptive filter.

Mehra offered four distinct categories such as Bayes estimate,covariance matching,correlation,and maximum likeli-hood(ML)for the adaptive filter.The procedures used to implement the adaptive Kalman filter are classified into three main methods:innovation-based adaptive estimator(IAE),multiple model adaptive estimate(MMAE),and adaptive fading Kalman filter(AFKF)in[9].MMAE is an important aspect in multi-model adaptive control,which is appropriate for systems with uncertain parameters or variable structure[10],[11].The central idea of multiple model(MM)was put forward by Magill in 1956.This algorithm has become a mainstream approach to study estimation problems in hybrid systems.Meanwhile,the interactive multiple model(IMM)algorithm and static multiple model algorithm are most widely used in what.In MMAE method,the state estimation of the system is obtained by the weighted sum of each subfilter’s estimation with the likelihood function of unknown elements.Thus,this method can adapt to the systems with uncertain or unknown parameters[12].

The contributions of this paper are to propose the MMAEUKF method and apply this proposed filtering approach to a SINS/CNS combined navigation system.At the same time,we carry out a simulation with motion of ballistic missile and make comparisons among EKF,MMAE-EKF,UKF,and MMAE-UKF algorithms.Simulation results are provided to indicate that MMAE-UKF can obtain the highest navigation precision.

The organization of the remainder of this paper is shown below.Multiple model adaptive estimation method is presented in Section II.Section III describes the MMAE-UKF algorithm in detail.In Section IV,the ballistic missile motion and integrated navigation is specified.Then,Section V gives the simulation conditions and results.In the end,conclusions are drawn in Section VI.

II.MULTIPLEMODELADAPTIVEESTIMATION

This section primarily researches the multiple model adaptive estimate algorithm,which is composed of a set of parallelfilters and a hypothesis testing.In this filter bank,each filter has a specific model of the system which is expressed by independent vector parameters.Then,each filter forms estimated value of the current system state according to the input vector and self-model independently.Making use of the current state estimate to calculate predicted measurement,the residual error is obtained through subtraction of predicted measurement value from true value[13].Then,based on the true vector parameters and measurement,hypothesis testing applies the residual error to compute the conditional probability of each model,and the obtained probability is applied to measure the estimation accuracy of each filter state.In the end,we obtain the optimal estimate of the system state with the state estimation of each model multiplied by the corresponding weights[14].The MMAE architecture is demonstrated in Fig.1.

A.Bayesian Estimate

Multiple model adaptive estimation is a recursive estimator,which utilizes a group of filters with unknown elements.The elements are the parameters of process noise covariance matrix,indicated by the vector pp .A group of distributed values are produced from the probability distribution function about p ,given by p( pp ),and{ pp(l)；l=1,2,...,M}where M is the sub-filter’s number.The aim of the filter estimate is to decide conditional probability of the lth element pp(l),which is provided the current-time measurement y~yk.The application of Bayesian law is shown as follows[15]:

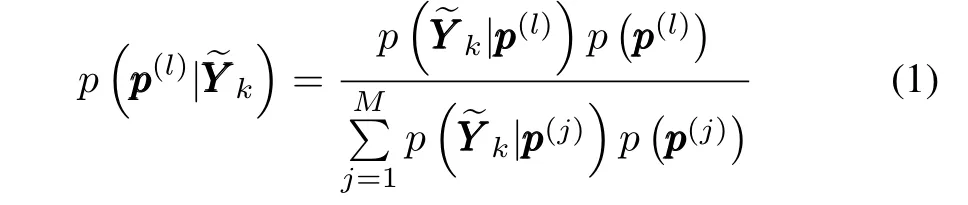
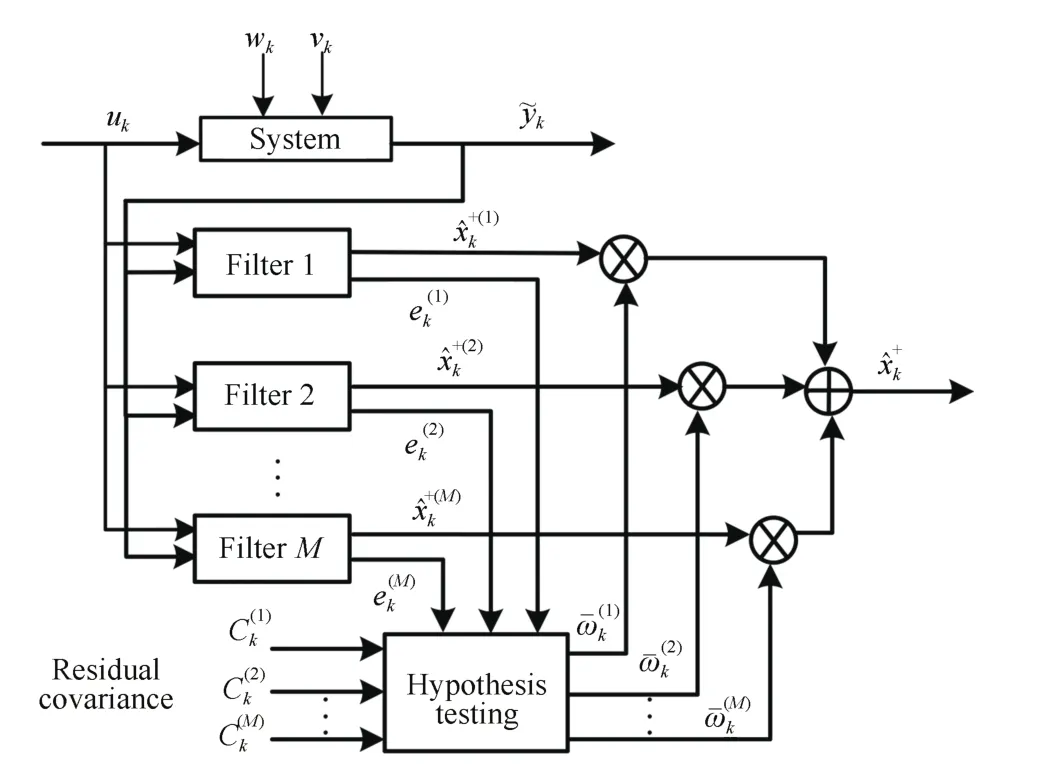
Fig.1.The MMAE architecture.

And the posteriori probability density function calculated by

The conditional mean estimation is the sum of parallel filters estimations by weighting as below:

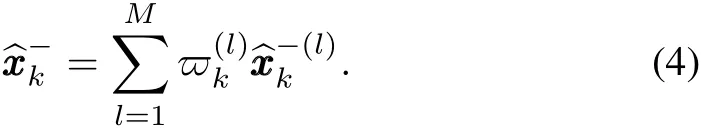
Meanwhile,the state estimations’error covariance is calculated through

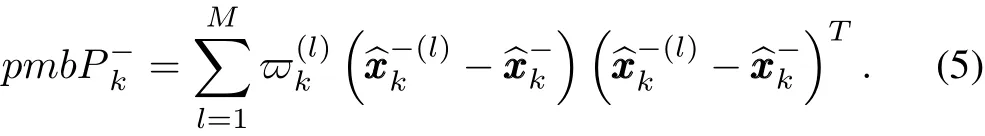
B.Likelihood Equation

The likelihood function for the residual of measurement is constructed in this part.Primarily,the residual error is given by

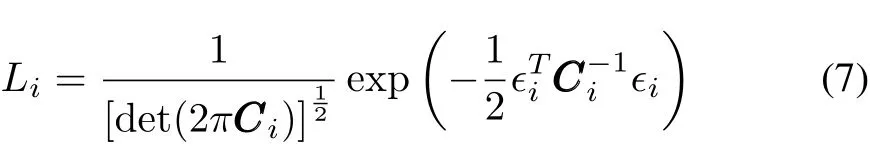
When i=0,є0= eek, CC0=.Therefore,the likelihood equation can be expressed by

C.Adaptive Laws

This part presents the adaptive laws.The current measurements are just applied to update law given by(3)in standard MMAE method.Thus,the update law on account of the likelihood function is obtained through

III.MMAE-UKF ALGORITHM

In what follows,we consider the form of the discrete nonlinear system model

where xxk∈Rndenotes state vector of system, uuk∈Rmis input of the known control, zzk∈Rqis the measurement,wk～N(0, QQk)is the noise sequence of process,and vvk～N(0, RRk)is noise of measurement.The vectors wwkand vkare mutually independent and zero-mean additive noise sequence with covariance matrices QQkand RRk,respectively.The statistical properties of initial condition xx0of(11)are denoted by the mean and variance[16].

In order to resolve this problem of nonlinearity and non-Gaussian,the UKF algorithm based on unscented transformation(UT)is provided to improve the EKF algorithm.UT adopts sigma symmetric sampling method,which needs 2n+1 sigma points.The core of UKF algorithm is to select a group of sigma points near the,and PPP(k|k)indicate the mean and covariance of the sigma points,respectively.Under the hypothesis that the dimension of the state variables is n×1,2n+1 sample points are obtained

where λ = α2(n+ κ)-n is an adjustment factor and α ＞ 0 is a scale factor.

First,the basic UKF algorithm is detailed as follows:

1)Initialize:

2)Calculate sigma points:

3)Time update:

a)Sigma points spread by the system equation are

b)Sigma points propagated by the measurement equation are

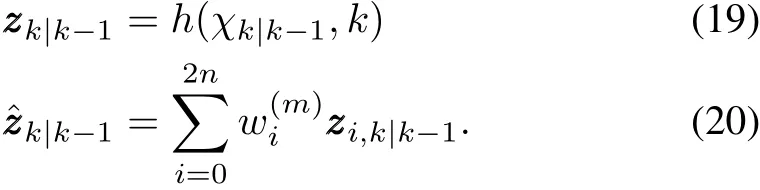
4)Measurement update:

a)Estimate covariance of the prediction measure

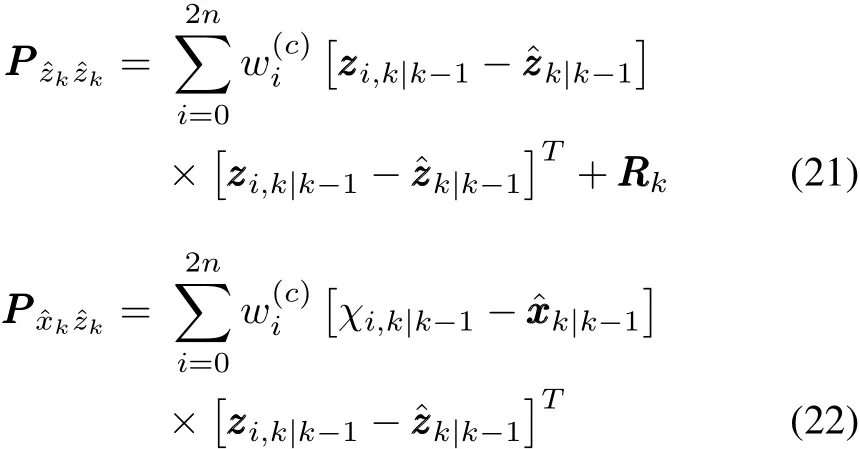
b)Compute filter gain and covariance correction

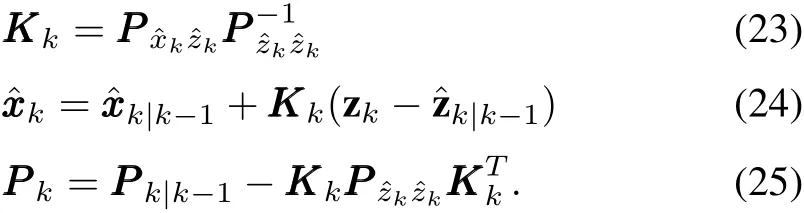
Then,the MMAE-UKF algorithm is summarized as follows:

1)Initialization:

2)Estimate with UKF:

a)Calculation of sigma points;

b)Time update;

c)Measurement update.

3)Calculate likelihood equation using multiple model adaptive estimation

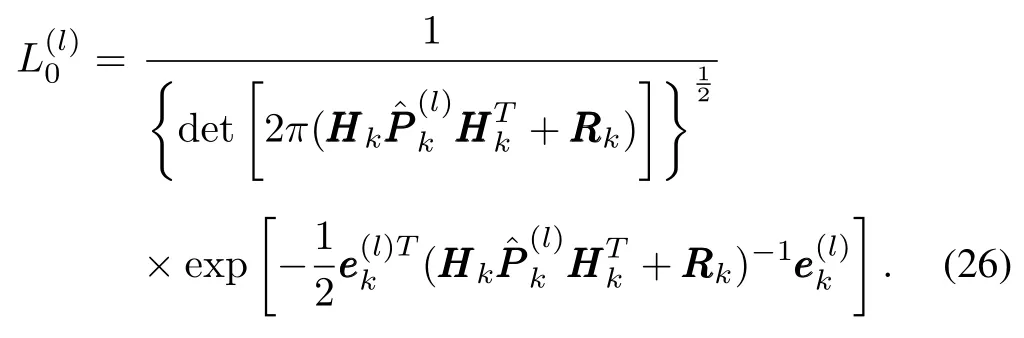
Evaluate weights and normalize the importance weight to be a normalization constant

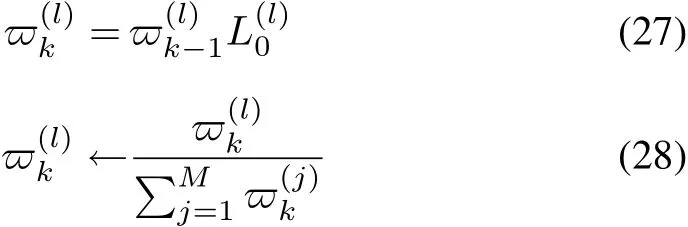
for l=1,2,...,M.

4)Output

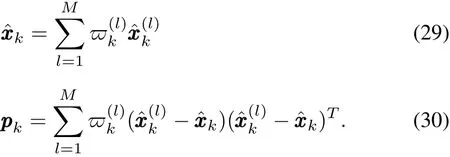
IV.STATE ANDMEASUREMENTMODEL

A.Dynamics of Ballistic Missile

The movement of the missile can be divided into three phases,including the vertical rising part of the boost stage,the turning part of the boost stage and the final flameout stage[17].Under the assumption that ballistic missile is a particle and the earth is a fixed sphere,then the nonlinear dynamics model of the missile is shown as

where P is thrust force,Xdis air drag,and g is gravitational acceleration.And,g=g0(Rm/r)2,r=

where θ is the angle of pitch about the launching point under the gravity coordinate system,θ0is angle of pitch when launching,and θkshows the angle of pitch at the end of the boost stage of turning.

To avert the coordinate transform as a result of the earth’s rotation,the gravity coordinate system at the launch site is turned into inertial coordinate system.Then,the position of the ballistic missile is obtained by making use of the velocity’sfirst-order integration under the inertial coordinate system at the launch site,and the derivative of velocity is taken to obtain the absolute acceleration of ballistic missile.The accelerometer’s error is modeled as the first-order Markov process[18].Because of the relative equation(33)between absolute acceleration and apparent acceleration αib,we can gain the accelerometer output through the conversion of α into the coordinate system of the ballistic missile and the addition of the first-order Markov process.Meanwhile,the gyroscope output is obtained through adding the Gaussian noise to attitude angular velocity in the missile coordinate system.

The accelerometer output is:

After the first-order calculation,the gyroscope gains the attitude angular rate denoted by,,,then the velocity of attitude angle is given by

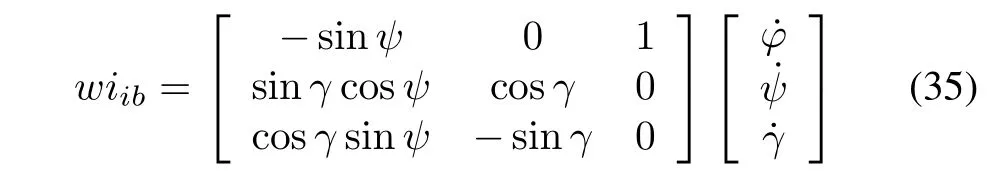
where ϕ,ψ and γ express the angle of pitch,yaw,and roll,respectively.

Based on this assumption that the system has additive noise,the mathematical model can be indicated by

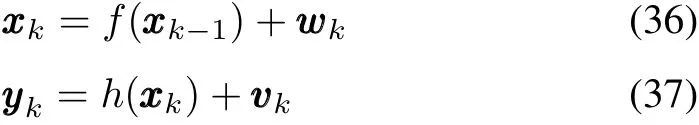
B.SINS/CNS Integrated Navigation

High accuracy and high availability of navigation information are necessary for many nonlinear systems.The integrated navigation system can make the most of each subsystem’s information,and further enhances the precision of navigation information.Thus,we combine SINS with CNS to build integrated navigation system that utilizes SINS as the main body.Next,we correct the attitude angle,velocity,and position information in SINS by the information obtained from CNS[19].Employing improved filter technology,the errors of accelerometer,gyro or other navigation parameters are obtained in the system of combined navigation.

The SINS/CNS integrated navigation system uses the scheme of strap-down that is connecting the carrier with star sensor,which has the advantages of flexible application,low cost,and a simple structure,but the disadvantage of requiring a larger field angle due to the star sensors only working in a dynamic environment[20].Fig.2 shows the work process of integrated navigation system.In view of specific force and angular speed that is obtained from missile trajectory generator,the SINS can get the inertial instrument output.Then,the SINS attitude information turns up.Meanwhile,this CNS subsystem obtains the attitude of vehicle through the star sensors’measured information and directly outputs the angular error information.After filtering the angular error,we gain the SINS’s attitude-angle error estimate and the final output of this integrated navigation system.

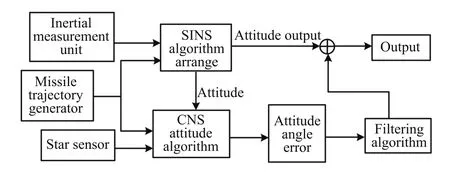
Fig.2.The flow diagram of SINS/CNS integrated navigation.

Integrated navigation systems are more accurate than simple system of inertial navigation because the fixed star’s orientation in the inertial space is essentially constant.Though the precession of the earth’s polar axis,parallax,and the star sensors’aberration cause small changes in the direction of the stars,they result in an attitude error of less than 1◦.So,the star sensor is equivalent to gyro without drifting,and we can apply the astronomical measurements of inertial equipment error.

In this integrated navigation system,the CNS usually applies the star sensors to seek starry sky,capturing the stars,recognize star charts,and then drawing the fixed stars’imaging location.After image recognition,we eventually calculate the attitude matrix of star sensor to gain the attitude information[21].The star sensors output the attitude angle’s observed value under the inertial coordinate system.In addition,indicates the transition matrix of attitude between the inertial coordinate system and the missile coordinate system.

And then,the attitude angle is indicated by

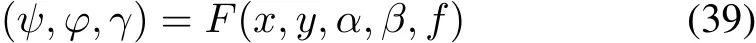
where(x,y)denotes the fixed star’s imaging position in the star sensors,(α,β)show the star’s right ascension and declination,respectively,and f shows the focal length of star sensor.

V.SIMULATION

In this part,we carry out simulations for SINS/CNS integrated navigation system of the missile to verify the filtering performance of this improved algorithm.The performance of four filtering methods(EKF,MMAE-EKF,UKF,and MMAEUKF)are also analyzed and compared.

A.Simulation Conditions

In general,we assume a set of time-varying parameters of process noise covariance,but in practice,we do not know these values of the system in advance.Therefore,due to the unpredictability of parameters,we need to adopt a method to generate an optimal random distribution.Here,we select two methods and contrast the simulation result of these two methods that are producing random numbers.The first method is linear congruence method to generate uniform distribution;the second is a Hammersley[22]quasi-random number generation method.Fig.3 shows a contrast between the first method and Hammersley quasi-random method,for randomly producing 250 elements between[0,1]which represents the range of generating distribution of random number sequences.From the figure,we see clearly that the Hammersley quasi-random method gives a better distribution of elements than uniform distribution,so we select the second method.

In this simulation,the filtering methods include the EKF,MMAE-EKF,UKF,and MMAE-UKF algorithms.Table I shows the initial simulation parameters.

In the system of integrated navigation,the true values of the parameters wgt0and wga0about process noise covariance are set as 9.6963E-05 and 4.8902E-04,respectively.It may be noted that the parameters wgt and wga in the EKF and UKF simulation process are chosen as wgt0and wga0.Since the 6×6 covariance matrix of process noiseis parameterized by wgt and wga,indicated as

TABLE I THEINITIALSIMULATIONPARAMETERS

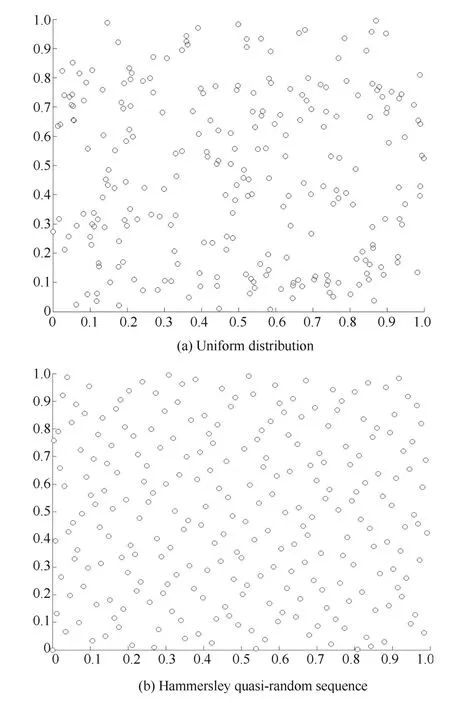
Fig.3.Comparison of uniform distribution and Hammersley sequence.

To highlight the advantage of filtering algorithm in this actual time-varying system,the Hammersley point set is used to distribute the parameters for each sub filter when setting the filter’s parameters.In MMAE,the filters’number is 10.

For the parameter setting of system,we assume the set of parameters for the process noise covariance matrix changes over time.That is to say,the total flight time of this ballistic missile is 300 seconds;during the first 100 seconds,the parameters of process noise covariance wgt and wga are half of wgt0and wga0,respectively.From 101 seconds to 200 seconds,the parameters wgt and wga are wgt0and wga0,respectively.During the last 100 seconds,the parameters wgt and wga are twice wgt0and wga0,respectively.

B.Simulation Result

This part provides simulation result with filtering performance of navigation system by the simulations,and includes some comparisons of the four filtering algorithms.From Figs.4-6,we can compare and analyze the error of yaw angle,pitch angle,and roll angle of the different filtering methods.According to the simulation results,the MMAE method indicates better performance in aspect of accuracy than the traditional EKF and UKF algorithms in information fusion.Furthermore,the MMAE method with UKF has obviously higher accuracy than the one with EKF algorithm in the state estimation process,and the MMAE-UKF algorithm gains the minimal attitude angle error.

To demonstrate the advantages and disadvantages of these four algorithm in navigation system more clearly,we assess the attitude error navigation performance of these filtering methods by the root mean square error(RMSE).The RMSE is defined by

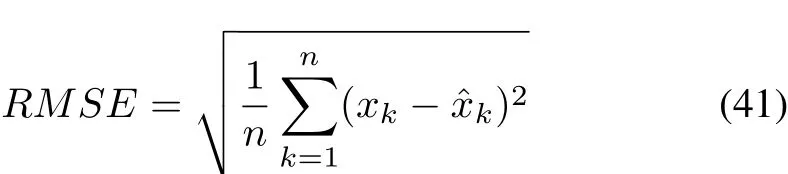
where n shows the number of available experiment data and(xk-)is error of true value and estimation value.

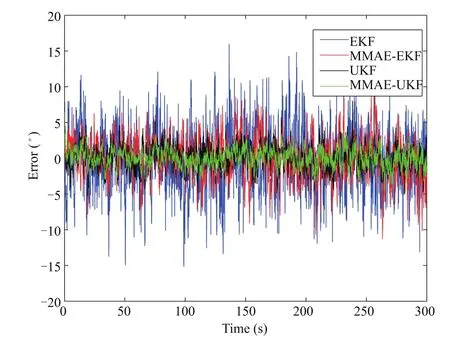
Fig.4.The error of yaw angle.

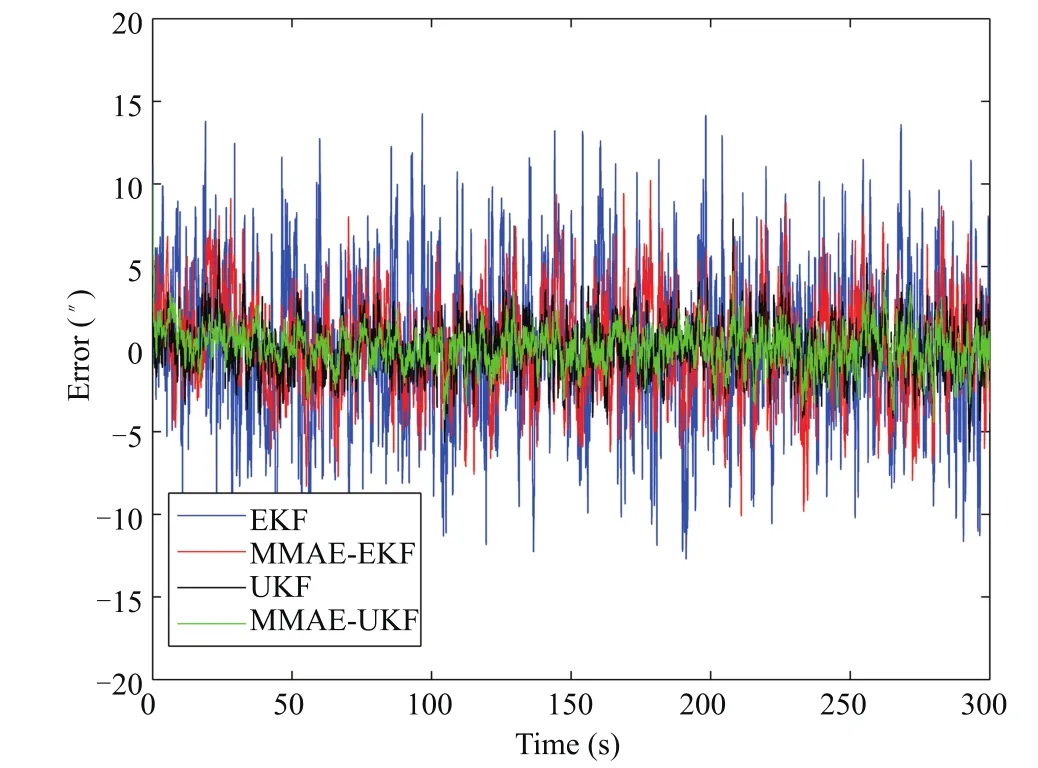
Fig.6.The error of roll angle.

Table II shows the simulation result with root mean square error of three estimated attitude angle for different algorithms.Thus,we can see that the optimal estimate of the following four algorithms is to employ this improved MMAE method with unscented Kalman filter.

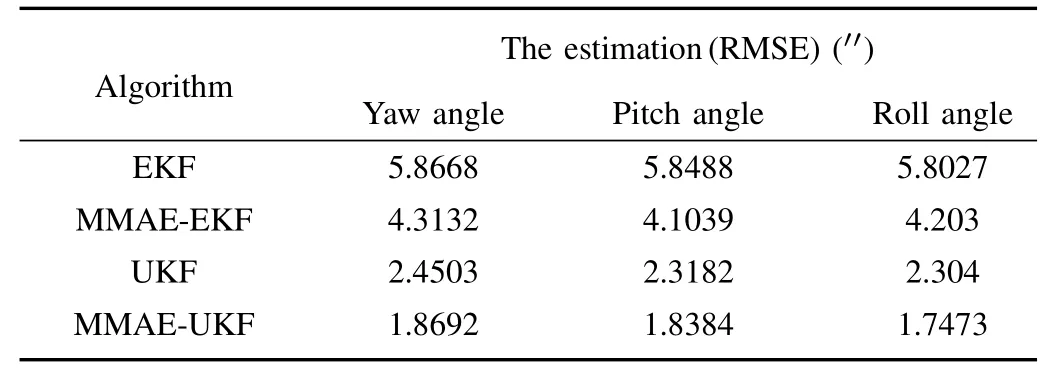
TABLE II PERFORMANCE OFDIFFERENTFILTERINGALGORITHMS

VI.CONCLUSION

This paper has derived a new filtering approach based on multiple model adaptive estimate method,which is suited for nonlinear system-Ballistic Missile Motion.In this method,we design UKF as sub filter in MMAE rather than EKF to obtain the estimate of system state.To indicate the navigation performance of the improved filtering algorithm more clearly,we carry out the simulations,and the behaviors of EKF,MMAE-EKF,UKF,and MMAE-UKF have also been compared and analyzed in the SINS/CNS integrated navigation system.Based on the simulation results,compared with conventional EKF and UKF methods,MMAE-EKF and MMAE-UKF algorithms obtain better navigation performance.MMAE-UKF method can gain the highest navigation accuracy at the cost of the highest computational cost,and the improved methods can meet the demand of the ballistic missile’s movement.With a view that integrated navigation system has some uncertain factors,filtering methods with adaptive parameters are to be studied and some real experiments are to be done in the future.