光纤陀螺随机漂移的混沌特征分析
2018-12-22狄世彦朱奎宝邓学文
狄世彦,李 贺,朱奎宝,邓学文
(中国航天科工集团第二研究院706所,北京 100854)
0 引 言
光纤陀螺随机漂移可看作是一组具有非线性、非平稳和弱时变特性的随机时间序列,这些特点限制了光纤陀螺向高精度领域的发展,因此,建立准确有效的随机漂移模型并进行预测补偿是有意义的。目前,时间序列的分析预测方法主要有两种:一种是应用较早、发展较成熟的传统统计建模方法,如自回归模型(AR)和自回归滑动平均模型(ARMA)[1,2],这种方法要求时间序列必须是平稳的、正态分布的零均值序列,对于慢时变的陀螺信号,其模型的预测精度受到很大的限制;另一种是以神经网络为代表的现代非线性预测模型,如人工神经网络、小波分析、模糊逻辑等等,神经网络可以很好地逼近非线性函数,但其遵循的经验风险最小准则降低了算法的泛化能力,且易陷入局部最小值。本文研究的目的是找到一种泛化能力强、预测准确的光纤陀螺随机漂移模型。
1 光纤陀螺随机漂移的混沌特征
1.1 混沌运动
所谓混沌,是指在确定的非线性动力系统中存在的一种貌似随机的运动。对于确定性动力系统,可由给定的初值推知系统未来的发展状况,对于非线性系统,系统对初值相当敏感,即使初值有微小的变化,也将引起系统长期状态的极大变化,如著名的“蝴蝶效应”。混沌是确定性系统内在随机性的反映,它与受外部因素影响的随机性不同,系统可用确定性的方程描述,在不附加任何其它随机因素的情况下,系统仍会表现出一定的类似随机行为。通常的随机性由于不服从确定的动力学规律,其随时间的发展是不可预测的,但混沌发生在确定性系统中,其服从一定的动力学规律,因此,混沌系统在短时间内是可以预测的。混沌理论最早来源于法国著名数学家Poincare在研究三大球体时提出的假设[3],他意识到三大球体受到微小的干扰,将可能导致完全不一样的运行轨道。1963年美国气象学家Lorenz在研究大气流动问题时发现了混沌现象,1975年华人学者李天岩和美国数学家York首次给出了混沌的数学定义,并证明:一个周期为3的轨道存在,则一定有混沌现象出现。
混沌运动客观存在于自然界中,它是一种不规则的、非常复杂的运动形式,主要有以下几个特征:
(1)长期运动对初始条件极为敏感
初始状态非常靠近的两个点,其轨道的差距随着时间的推移会成指数扩大,这使得混沌系统的长期演化行为变得不可预测。
(2)相空间中存在奇异吸引子
吸引子是动力学过程的轨迹,在经过足够长时间的发展之后,其将逐渐达到收敛的状态或状态的集合。动力系统有3类吸引子:平衡点、极限环河奇异吸引子,平衡点是系统运行轨迹收敛到一个不动点,极限环是系统轨迹呈现周期性,而混沌系统的奇异吸引子在轨道中表现出无限的扭曲和折叠。平衡点和极限环的维数常为整数,混沌吸引子由于是分形结构而具有分形维。
(3)内在随机性
混沌系统随机性的根源是来自确定性系统的内部,并不仅仅依赖于外部因素的干扰。
(4)标度不变性
混沌是一种无周期的有序,混沌系统的演化会出现分叉行为,并遵从Feigenbaum普适常数。
当今社会上的混沌现象无处不在,不同行业的学者都可以在自己的研究领域找到混沌现象,从20世纪90年代开始,混沌的研究已经开始在学科间相互渗透,无论是物理学、生理学、电子学,还是气象学、经济学、音乐,混沌理论都有着广泛的应用。
1.2 光纤陀螺随机漂移混沌特征的判定
时间序列是自然界中某一个或一组变量按时间先后和相同时间间隔排列的一组观测数值,现实生活中如股市指数、地区降雨量、河流径流量等都可看作是时间序列,这些序列均被发现含有混沌特性[4]。为了揭示混沌时间序列貌似随机现象的背后可能隐藏的规律,需要采用时间序列分析方法来提取序列中含有的准确信息,并通过建立相应的数学模型来对时间序列的未来值进行预测,以给人们的生活带来更多的帮助。
混沌运动来自于非线性动力学系统,这使得混沌时间序列具有非线性、非平稳的特征,因此,基于统计学理论的线性回归模型预测方法对于混沌时间序列的预测是困难的,而基于数据的各种机器学习方法在混沌时间序列的预测中逐渐得到应用[5]。要采用混沌理论的相关知识对时间序列作出较为精确的预测,必须判断时间序列是否具有混沌特性,常用的混沌时间序列判别方法主要有:功率谱法、Poincare截面法和最大Lyapunov指数法,其中最大Lyapunov指数法应用较多[6]。
混沌运动的一个基本特征是长期运动对初始条件非常敏感,极其相近的初值所运行的轨道,其差距会随着时间的推移按指数形式扩大,而Lyapunov指数能够定量描述出两个轨道的发散特征。在识别混沌运动时,通常只需要计算最大Lyapunov指数λl即可,若λl为正,则表明系统运行轨道有发散特征,呈混沌运动;若λl为零,则表明系统运行轨道对初值不敏感,呈周期运动;若λl小于零,则系统的长期运行轨道与初值无关,系统运动轨迹最终将收敛到一个平衡点。
求取时间序列的最大Lyapunov指数λl的方法较多,常用的有雅克比法和Wolf轨线法[7,8]。Wolf法直接根据相轨线、相体积、相平面等的演化来估计Lyapunov指数,由于光纤陀螺随机漂移可看作是非线性、非平稳的时间序列,因此,本文采用Wolf法来计算随机漂移的最大Lyapunov指数。在相同的环境条件下,采集同一型号的8只光纤陀螺的常温静态数据,每只陀螺的采样时间为3600 s,采样间隔1 s,为了消除奇异点和部分噪声的影响,计算前对采样数据进行零偏补偿和低通滤波去噪,如图1所示为其中一组光纤陀螺随机漂移的实验数据。

图1 预处理后的光纤陀螺随机漂移
利用wolf法计算最大Lyapunov指数的主要过程如下:
任取一组光纤陀螺随机漂移作为计算的时间序列{x(n),n=1,2,…,N},N为数据长度,用嵌入维数m和延迟时间ττ对随机漂移进行相空间重构(关于相空间重构的内容在后续章节介绍),M是重构空间的相点个数,M=N-m-1,则重构空间中的相点可表示为
X(i)=[x(i),x(i+τ),…,x(i+(m-1)τ)]
i=1,2,…,N-(m-1)τ
(1)
(1)首先将重构空间中的相点X(i)作为一条基准轨线,并在基准轨线上选定一个初始点X(0);
(2)然后在X(0)的邻近范围内选定另一个点,可得两点间的距离向量L(0),要求L(0)满足L(0)<ε,ε为一大于0的阈值,且尽量使L(0)的方向与基准轨线在X(0)处的切向量不平行;
(3)追踪这两个点的演化,当经过一段时间后,L(0)变为L′(1),X(0)变为X(1),如果L′(1)>ε,则在X(1)附近再选定另一个点,得到距离L(1),满足L(1)<ε;
(4)重复上述过程,可得一组L(k)以及L′(k),用下式计算最大Lyapunov指数λl,K为总的迭代次数
(2)
运用上述方法所估计的8组光纤陀螺随机漂移的最大Lyapunov指数见表1。

表1 光纤陀螺随机漂移的最大Lyapunov指数
由表1可见,8组随机漂移的最大Lyapunov指数的估计值均大于0,这说明光纤陀螺随机漂移具有混沌特性,因此,采用混沌系统的相关模型对光纤陀螺随机漂移进行预测是可行的。
2 光纤陀螺随机漂移的相空间重构
2.1 相空间重构参数的计算
自然界和工程技术领域中的许多系统都是复杂的高维非线性系统,这些系统往往包含多个变量的信息,但通常情况下只能观测到系统的一维信息,即某一分量的时间序列。由于系统任一分量的演化是与其它分量相互作用的结果,这些相关分量的信息蕴含在任一分量之中,因此,从某一个分量的时间序列中就可以提取和恢复出系统内在的规律。相空间重构(phase space reconstruction,PSR)是找出数据隐藏演化规律的重要方法,是分析混沌系统的主要工具,其目的是将一维的时间序列通过重构的方式嵌入到多维相空间中,从而恢复出系统的吸引子。
Packard等于1980年提出了相空间重构理论以及广泛使用的时间延迟相空间重构方法[9],1981年Takens从数学角度证明了相空间重构的方法[10]。时间延迟重构法的基本思路如式(1)所示,Takens已经给出证明,当嵌入维数m≥2d+1(d是动力系统的维数)时,重构的相空间是一个嵌入映射,它能够保存非线性动力系统的许多特征,并在拓扑等价下恢复出这些特征。
前一节中已经通过计算最大Lyapunov指数证明了光纤陀螺随机漂移存在混沌特性,但一维的光纤陀螺随机漂移时间序列无法表现出系统的隐藏演化规律。因此,本文借助于相空间重构技术将一维的随机漂移时间序列嵌入到高维空间中,在高维空间中对随机漂移数据进行回归分析与预测。相空间重构的关键问题是如何正确选择嵌入空间维数m和延迟时间τ,m太小难以展示出系统的实际结构,m太大使得相点之间的关系变得模糊,增加了计算的复杂度。对于有限的数据,恰当的τ很重要,τ太小,则重构空间的相点相关性太强,系统信息无法完全显露,τ太大,则动力系统可能失真。
目前,计算嵌入维数m和延迟时间τ最常用的方法是由Kim等于1999年提出的C-C算法[11,12],这种方法认为两个参数是相互关联的,其取值相互依赖,并通过引入嵌入窗τw=m-1τ[13]将m和τ联系起来。由于C-C算法相对简单,计算量小,有较好的抗噪声能力,本文应用C-C法计算光纤陀螺随机漂移的两个相空间重构参数,计算的主要过程如下:
选取1.2节中的一组光纤陀螺随机漂移数据作为计算的时间序列xn,n=1,2,…,N,以嵌入维数m和延迟时间τ对其进行相空间重构,X(i)为重构空间中的一个点,则嵌入时间序列的关联积分为

(3)

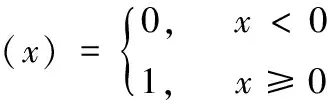
(4)
关联积分是个累积函数,表示相空间中任意两点间的距离小于r的概率,点间距离用向量差的无穷范数表示,定义检验的统计量
S(m,N,r,τ)=C(m,N,r,τ)-Cm(1,N,r,τ)
(5)
上式的计算方法为:将时间序列划分成τ个相互不重叠的子序列,子序列的长度为INT(N/τ),计算每个子序列的统计量

(6)
令N→∞,有

(7)
如果时间序列满足独立同分布,那么对于固定的m和τ,对于一切r,均有
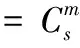
(8)
由于实际的时间序列是有限的,且时间序列各数据之间可能存在相关性,Sm,r,τ一般不为0。当m和r固定时,Sm,r,τ~τ曲线反映了时间序列的自相关性,最优延迟时间τ取Sm,r,τ~τ第一次过零点时对应的时间。此外,选择对应值最大和最小的两个半径r,定义差量
ΔS(m,τ)=max{S(m,rj,τ)}-min{S(m,rj,τ)}
(9)
当最大偏差ΔSm,τ最小时,重构的相空间点最接近均匀分布,重构的动力系统轨道最准确。由于ΔSm,τ为正数,最优延迟时间τ可取ΔSm,τ~τ的第一个局部极小值所对应的时间。
根据BDS统计的结论,当N≥3000,2≤m≤5,0.5σ≤r≤2σ时,Sm,r,τ~τ曲线能较好地表现出时间序列的自相关特性,σ为时间序列标准差,实际计算中取m=2,3,4,5,r=0.5σ,σ,1.5σ,2σ, τ∈0,20,并按下列各式计算

(10)

(11)

(12)

τw=(m-1)τ
(13)

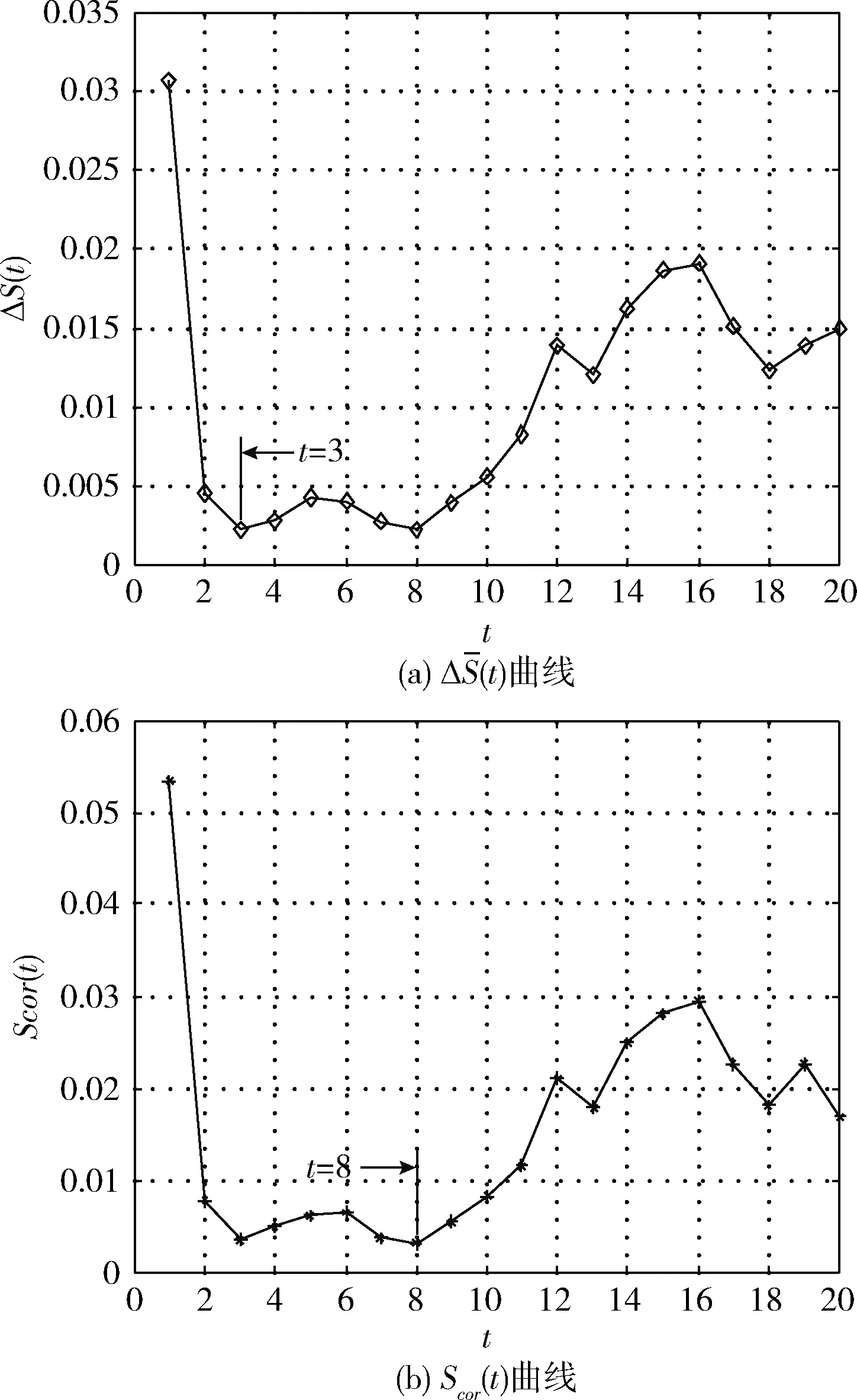
图2 C-C法计算随机漂移的相空间重构参数
2.2 重构的相空间图分析
为了从视觉上更加直观地看到光纤陀螺随机漂移所具有的混沌特征,可以根据C-C算法估计的最佳延迟时间τ=3作出光纤陀螺随机漂移时间序列的相空间图来进行定性分析,这里将随机漂移时间序列的xt+τ值作为xt的函数画在二维空间图中,如图3(a)所示。为了与随机漂移的相空间图作对比,用Matlab的rand函数在区间(0,1)内随机产生3600个数据,并将随机数时间序列的相空间图同样按延迟时间τ=3画在二维空间图中,如图3(b)所示。

图3 时间序列的相空间
由图3可见,光纤陀螺随机漂移时间序列的相空间图与随机数时间序列的相空间图在直观上存在着明显的差异:随机漂移时间序列的所有点在相空间图中紧紧纠缠在一起,形成一个近似的圆形,且图面仅占据二维图中间的一部分,而随机数时间序列的所有点在相空间图中均匀分布,几乎填满了整个取值空间。光纤陀螺随机漂移时间序列的相空间图所具有的复杂形状,与随机数时间序列的相空间图完全不同,两者存在本质上的差别。由此可以推断,光纤陀螺随机漂移时间序列存在混沌特征,这与1.2节中计算的最大Lyapunov指数值所表征的结果相一致。
对光纤陀螺随机漂移进行相空间重构的目的是为了将一维的标量时间序列重构成体现系统特征的高维空间向量,这些向量与现代非线性预测模型相结合,可以对光纤陀螺随机漂移进行回归分析与预测。
3 结束语
本文介绍了混沌运动的相关知识,并通过计算最大Lyapunov指数验证了光纤陀螺随机漂移所具有的混沌特性。为了有效地提取出随机漂移的混沌特征,本文使用相空间重构的方法将一维的随机漂移时间序列嵌入到一个高维的辅助空间中,重构参数由C-C法计算得到,根据相空间重构的参数绘制了随机漂移时间序列和随机数时间序列的相空间图,两种图形存在的较大差异进一步说明了光纤陀螺随机漂移存在的混沌特征。
