支持度和置信度自适应的关联规则挖掘
2018-12-22林甲祥巫建伟陈崇成张泽均舒兆港
林甲祥,巫建伟,陈崇成,张泽均,舒兆港
(1.福建农林大学 计算机与信息学院,福建 福州 350002;2.国家海洋局第三海洋研究所海洋环境管理与发展战略研究中心,福建 厦门 361001;3.福州大学 空间数据挖掘与信息共享教育部重点实验室,福建 福州 350116)
0 引 言
关联规则是数据挖掘一个重要研究主题,在购物篮分析、医疗诊断、股票存货分析、Web日志挖掘、客户市场分析、生物信息资讯等领域有着广泛的应用[1]。文献中提出的大多数关联规则挖掘方法采用两步骤的策略,首先从数据集中寻找所有频繁项集,然后由这些频繁项集生成强关联规则,算法的原理简单且易于实现,其中第一步频繁项集的生成是算法的关键,典型算法如Apriori、FP-tree等[2]。
以频繁项集搜索为核心的关联规则挖掘算法,在支持度的约束下进行频繁项集搜索,在置信度的约束下进行强关联规则确认。目前,许多关联规则挖掘实践中,最小支持度(minsup)和最小置信度(minconf)参数的取值方法仍是由用户根据先验知识进行人为的指定,一方面,非专业关联规则算法用户,对算法参数的取值一般具有较大的主观随意性、往往很少考虑参数取值的科学性;另一方面,挖掘模型中支持度和置信度阈值的不同取值,对挖掘过程中频繁项集的大小、自连接产生候选项集的规模、挖掘结果中关联规则的数目有着显著的影响。从算法设计的角度实现关联规则支持度和置信度参数的科学化和自适应化取值,文献中还鲜有相关的研究成果报道。因此,拟在分析事务数据集中所有项的支持数和所有规则的置信度的基础上,使用统计拟合技术,对支持度和置信度阈值的自动化确定技术进行研究,提出基于支持度和置信度自适应技术的无参化关联规则挖掘解决方案,以期降低关联规则挖掘行业化应用的门槛。
1 相关研究进展
近年来,研究人员在提高关联规则计算效率、寻找更紧致数据结构、处理的数据类型扩展等方面做了大量的研究。典型工作如:增量式关联规则挖掘方面,Nath等[3]对增量式关联规则挖掘算法进行了综述。基于特定数据结构的关联规则挖掘方面,Vo等[4]对基于N-list和包含概念的频繁项集挖掘PrePost算法进行研究,在N-lists创建和交互中融合了Hash技术,对算法进行了改进。此后,Huong等[5]对基于N-list和考虑权重的频繁项集挖掘算法进行了研究。Maria Luna等[6]提出了一种称为倒排索引压缩(inverted index compression)的数据结构,能够用于很多现有的关联规则挖掘算法,用于提高算法的效率。Anand等[7]为提高关联规则挖掘的效率,提出了基于横二叉树(Treap)数据结构的关联规则挖掘算法。牛新征等[8]提出了一种基于FP-tree的快速关联规则隐藏算法,避免了遍历原始数据集产生的大量I/O时间,减少了关联规则隐藏处理对原始数据集的影响。分布式&并行关联规则挖掘方面,Wang等[9]使用微处理器技术对关联规则的并行化和效率提升进行了研究。Vu等[10]针对频繁模式搜索,开展了多核共享存储器的并行关联规则挖掘研究。Liu等[11]面向大数据,提出了一套基于MapReduce和最大频繁项集的启发式多流程关联挖掘解决方案。基于智能技术的关联规则挖掘方面,Sohrabi等[12]对基于元胞自动机的频繁模式挖掘进行了研究,并与Apriori、FP-Growth、BitTable等知名算法的效率进行了对比分析。Zou等[13]提出了一种基于模糊概念格的关联规则挖掘及其动态更新算法。Heraguemi等[14]将使用多重合作策略的蜂窝算法用于关联规则挖掘。基于关联规则的应用研究方面,Tseng等[15]对事务数据库中高效用项集的关联规则挖掘进行研究,提出了效用模式增长算法UP-Growth及其改进算法UP-Growth(+)。Leu-ng等[16]针对大数据环境下的Web页面推荐,提出了一套按位(bitwise)并行关联规则挖掘方法。何明等[17]为了提高个性化推荐效率和推荐质量,平衡冷门与热门数据推荐权重,提出了优化Apriori算法且适合不同测评标准值的k前项频繁项集挖掘算法。
在关联规则算法参数取值研究方面,Sarath等[18]使用二进制粒子群优化策略,对关联规则挖掘进行研究,无须指定最小支持度和最小置信度参数,只需指定要获得的规则的数目。虽然,一些基于智能技术的关联规则挖掘,通过问题解空间的全域搜索,无须设置最小支持度和最小置信度参数的值,即可获得支持度最高、置信度最高的若干强关联规则,但需要很大的计算量。对于关联规则挖掘算法参数的自适应取值研究,文献中未见相关成果报道。
2 核心概念与挖掘流程
2.1 相关概念
令交易事务数据库中所有商品种类的集合为I=i1,i2,…,im,其中m为自然数,表示数据集中不同商品的数目。D为规模为N的事务集,即数据库中交易记录的集合,N为交易的数量(记录数),其中每一个事务t是一个项集,表示为t=t1,t2,…,tn,ti∈I,n为自然数,n≤m,表示事务t中商品的数目(项数),即t⊆I。对于项集X,若X中含有的项数为k,则称X为k-项集;若X⊆t,则称事务t包含I的一个子集X。
事务集D中的关联规则是一种由支持度(support)和置信度(confidence)约束的蕴含式X⟹Y,其中X⊂I,Y⊂I且X∩Y=∅,支持度表示规则的频度,置信度表示规则的强度。
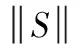
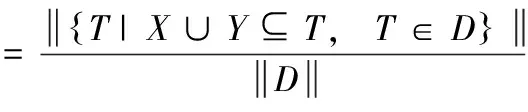
(1)
在事务集D中,项集X的支持数是D中包含X的交易数,记为support_count(X),如式(2)所示,support_count(X)∈{0,1,…,N},即X的支持数是不大于交易记录数N的一个自然数
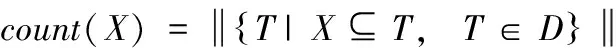
(2)
在事务集D中,规则X⟹Y的置信度是D中同时包含X和Y的交易数与包含X的交易数之比,记为confidence(X⟹Y),如式(3)所示,confidence(X⟹Y)∈[0,1]
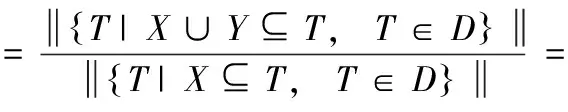
(3)

2.2 关联规则挖掘的一般流程
现有大多数关联规则挖掘算法采用两阶段频集思想,首先获得事务集D的所有频繁项集,然而基于频繁项集进行关联规则生成,挖掘的一般流程包括图1所示的4个核心步骤。

图1 基于频繁项集的关联规则挖掘的一般流程
图1中,步骤1指定参数minsup和minconf的值是关联规则挖掘的前提;步骤2在事务集中寻找所有k阶频繁项集是关联规则挖掘的核心计算花销所在,往往需要对事务数据集进行多趟扫描;在步骤2得到所有k阶频繁项集后,步骤3和步骤4则较为容易。
3 自适应关联规则挖掘
3.1 算法思想
支持度和置信度自适应关联规则挖掘算法AdapARM(adaptive association rule mining)的基本思想是:以事务集D中所有项的支持数和频繁项集能产生的所有规则的置信度数据为依据,用数据说话、由数据决定支持度和置信度参数的取值,在支持数和置信度数据从大到小有序排列的基础上,通过递减序列不低于3次的多项式曲线拟合,寻找拟合曲线切线斜率变化速度(二阶导数)首次为0、即拟合曲线凹凸转换的拐点位置,作为最小支持数mincount和最小置信度minconf的取值。
由于支持数和置信度序列的单调递减性和多项式拟合曲线的连续性,二阶导数为0的地方是曲线变化由缓到急或由急到缓的转折点,将二阶导数首次为0的地方选取为支持数和置信度参数的阈值,具有较为科学的统计和数理分析依据。至于多项式拟合曲线的次数,由于2次多项式无法较好拟合支持数和置信度序列的单调递减性,而1次多项式退化为直线,也无法用于确定参数的科学取值,因此使用不低于3阶的多项式进行曲线拟合,从技术上确保了二阶导函数及其支持数和置信度参数取值的存在性。
总之,算法通过数学的方法,使用拟合支持数和置信度序列的曲线及其二阶导函数,确定数理意义上最适合的数值作为关联规则挖掘的mincount和minconf阈值,能够有效解决关联规则挖掘算法对先验知识的依赖问题。
3.2 核心步骤
传统关联规则挖掘通常要求算法用户根据先验知识事先指定最小支持度和最小置信度参数的值,而提出的算法AdapARM让数据说话、根据数据集自身的特性,自适应地确定最小支持数和最小置信度的值。AdapARM的核心步骤如图2所示,其中步骤2和步骤5:最小支持数和最小置信度的自动确定,是核心研究内容。
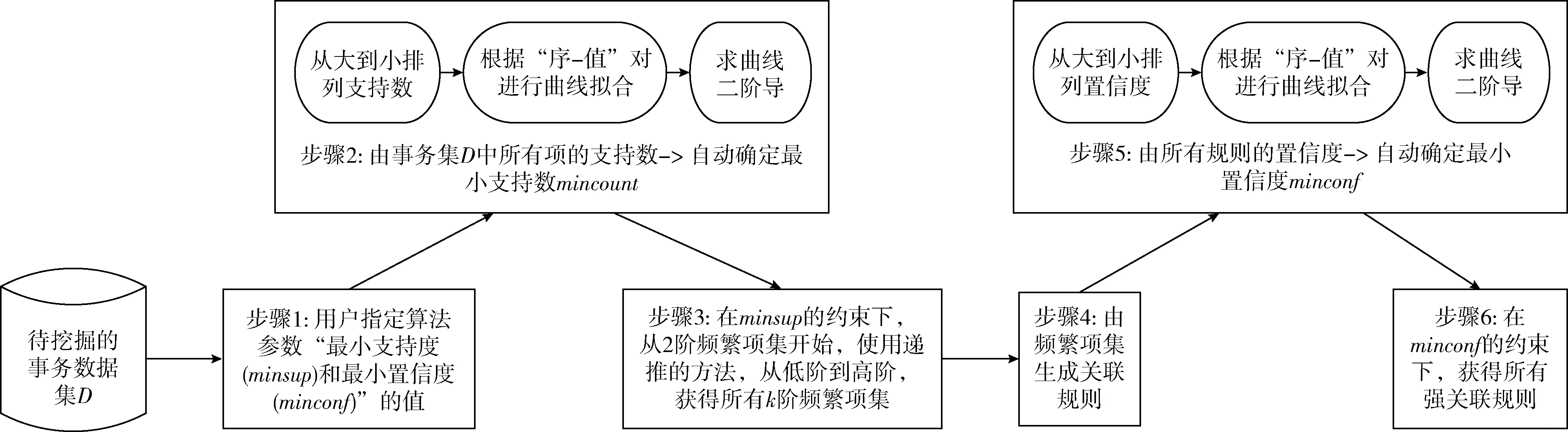
图2 支持度和置信度自适应的关联规则挖掘的核心步骤
3.3 支持度和置信度自适应的实现
首先,将事务集D中各商品(项)的支持数或某个规则的置信度,按从大到小的顺序进行排序,建立“序-值”对序列(xp,yp)p=1,2,…,t(如图3所示),其中序号值xp=p,序列值yp随着序号值xp的递增而递减,即当xp 图3 面向项支持数和规则置信度的“序-值”对 对于支持度,yx为某个项ix在事务D中支持数(即yx=support_count(ix)),“序-值”对的数目t为事务数据集D中商品(项)的数目,即t=m。 对于置信度,yx为频繁项集生成的某个规则的置信度(即yx=confidence(X⟹Y)),“序-值”对的数目t为所有k阶频繁项集能够产生的关联规则的数目。 然后,基于“序-值”对数据,以序号值为x、序列值为y,建立有序的平面坐标(xv,yv)点序列(v=1,2,…,t),并采用多项式进行曲线拟合。拟合的多项式曲线如式(4)所示 (4) 紧接着,求取以获得拟合曲线的二阶导函数f″(x),如式(5)所示 (5) 从mincount和minconf的取值方法可见,其数值取决于所拟合的曲线f(x),而f(x)主要由有序支持数或置信度构造而来的平面点序列(xv,yv)所刻画。因此,可以说按提出方法自动获得的mincount和minconf的取值,与事务集D中项的支持数与产生的规则的置信度的分布情况密切相关,能够自适应地贴合数据集自身的特性。 支持度和置信度自适应的关联规则挖掘算法AdapARM的伪代码如下: (1)C1= find_candidate_1-itemsets(D); //get all items’s support count (4)findminix0,wheref″(x0)=0; //compute second derivative and get the minimal resolution (6){L1,L2, …,Lk}=find_all_frequent_k-itemsets(D,mincount); //accordingmincount (7){R1,R2, …,Rt}=generateRule_from_frequent_k-itemsets({L1,L2, …,Lk}); //generate rules (8)R′=sort_InDescOrder({R1,R2, …,Rt}); //sort rules in descending order according the rule confidence (9)y=h(x)=polynomial_curve_fitting(R′); //(x=order id,y=rule confidence) (10)findminix0,whereh″(x0)=0; //compute second derivative and get the minimal resolution (11)minconf=h(x0); //minconfis defined as the valueh(x0) (12){SR1,SR2, …,SRr}=find_strong_rules({R1,R2, …,Rt},minconf); //find strong rules withminconf 首先,扫描一次数据库,产生候选1项集C1; 紧接着,根据最小支持数阈值mincount,寻找所有k阶频繁项集。 再接着,通过所有k阶频繁项集,生成关联规则,并根据规则置信度值从大到小的方式对规则进行降序排列,对序号与规则置信度值进行多项式曲线拟合,寻找二阶导数为0的点x0,并将x0对应的拟合曲线函数值h(x0)作为最小置信度阈值minconf。 最后,依据最小置信度阈值minconf,筛选并获得所有强关联规则。 本节使用关联规则挖掘购物车Trolley数据集和开源软件R GUI里的Groceries数据集,对无须用户指定支持度和置信度参数的AdapARM算法的挖掘流程进行介绍,并对挖掘结果进行分析与讨论,从而验证提出算法在自动确定参数上的有效性和实用性。 Trolley数据集是很多数据挖掘教材中用于讲解Apriori和FP_Growth算法的某面包店仿真交易记录,总共有7个不同商品,有9条消费记录(即9行),如表1第2列所示。 Groceries数据集记录了某个杂货店一个月的真实交易记录,总共有169个不同商品,有9835条消费记录(即9835行),如表1第3列所示(仅列举前9条事务记录)。 步骤1 计算各数据项的支持数 遍历数据集,获得每个事务项的支持数,即获得候选1项集C1中各项的支持数,并按支持数从大到小对项进行排序,见表2(仅列举支持数最大的前7个项)。 表1 Trolley数据集和Groceries数据集 表2 数据集Trolley和Groceries中C1各项的支持数和排序号信息 步骤2 根据支持数从大到小排序数据项并进行曲线拟合 将Trolley数据集和Groceries数据集中各数据项的支持数,按从大到小的方式进行排序并使用3次多项式对数据进行曲线拟合,支持数与序值对应关系及其拟合曲线如图4所示。 Trolley数据项的支持数拟合曲线如式(6)所示 fT(x)=4.2857142857+3.5595238095·x- (6) Groceries数据项的支持数拟合曲线如式(7)所示 fG(x)=1486.065650975-42.7627470864·x+ (7) 步骤3 根据拟合曲线的二阶导函数求取最小支持数 (8) (9) 步骤4 根据最小支持数获得所有k阶频繁项集 根据获得的最小支持数(Trolley数据集为4、Groce-ries数据集为107),按照经典Apriori算法的思想,从一阶频繁项开始逐阶向上,获得数据集对应的所有k阶频繁项集。 Trolley数据集和Groceries数据集的所有k阶频繁项集 如表3所示,其中NULL表示“空”。 步骤5 根据频繁项集产生关联规则 根据获得的所有k阶频繁项集(见表3),为Trolley数据集和Groceries数据集产生关联规则,见表4。 步骤6 根据置信度从大到小排序频繁项集产生的规则 表3 Trolley数据集和Groceries数据集的所有频繁项集 表4 Trolley数据集和Groceries数据集频繁项集产生的关联规则 并进行曲线拟合 根据Trolley数据集和Groceries数据集频繁项集产生的关联规则的置信度,按从大到小的方式进行排序并使用3次多项式对数据进行曲线拟合,置信度与序值对应关系及其拟合曲线如图5所示。 Trolley数据集产生的规则的置信度拟合曲线如式(10)所示 hT(x)=0.9357665007-0.0199431001·x+ (10) 图5 从大到小有序的规则置信度及其拟合曲线 Groceries数据集产生的规则的置信度拟合曲线如式(11)所示 hG(x)=0.5230242099-0.0027245952246·x+ (11) 步骤7 根据拟合曲线的二阶导函数求取最小置信度 (12) (13) 步骤8 根据置信度阈值判断并获得强关联规则 根据设定的置信度阈值(Trolley数据集为0.6126373314、Groceries数据集为0.1158444298),获得Trolley数据集和Groceries数据集对应的强关联规则,见表5。 表5 Trolley数据集和Groceries数据集中的强关联规则 从上述数据挖掘流程可见,与传统算法需要用户预先指定最小支持度minsup和最小置信度minconf的具体数值不同,譬如最小支持度取值为50%、最小置信度取值为80%,提出的AdapARM算法不需要用户指定任何算法参数值,算法将根据不同的数据集,自动确定mincount和minconf的值。对Trolley数据集,自动确定的mincount值为4,minconf值为61.26373314%;对Groceries数据集,自动确定的mincount值为107,minconf值为11.58444298%。可见,AdapARM算法能够在用户不具备先验知识的前提下,自动确定参数minsup和minconf的值,且参数值与具体的数据集相适应,而不需要由用户进行算法参数值的人为指定,从而为关联规则挖掘任务的无参化运行提供了一种统计学意义上具有较高可信性的解决方案。 尽管如此,提出的方案经过进一步处理,仍能为实际关联规则挖掘任务的参数确定提供一定的借鉴。有效的阈值二次确定技术如:在最高支持数(或置信度)和自适应支持数(或置信度)之间,采用第一四分位数(Q1)、第二四分位数(Q2)、第三四分位数(Q3)作为最终选定的支持数(或置信度)的值。 总之,算法在确定支持度和置信度阈值时,通过计算所有数据项的支持数和所有规则的置信度,经从大到小排序后进行多项式曲线拟合,用数据说话、凭数据进行算法参数决策,使得算法在实际行业应用中走向科学,对于算法的推广应用乃至普及具有重要的实践意义。 本文提出了一个支持度和置信度自适应的关联规则挖掘算法AdapARM,能够在用户不具备先验知识、不指定支持度和置信度阈值的情况下,通过数据集自身的数据特征自适应地确定关联规则挖掘的支持数和置信度。支持度和置信度参数的自适应确定策略:是在数据集所有项的支持数、所有规则的置信度的有序序列的多项式曲线拟合的基础上,通过求取拟合曲线二阶导函数为零的点x0及其函数值f(x0),作为支持数和置信度阈值,进而挖掘统计意义上支持度和置信度较高的强关联规则。在关联规则挖掘标准数据集Trolley和标准数据集Groceries上的实验结果及分析表明,提出的方法对于关联规则挖掘算法的实施和推广具有一定的实际应用价值。
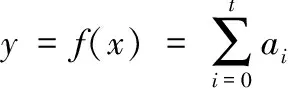
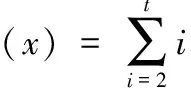

3.4 AdapARM算法实现




4 实验及分析
4.1 数据集说明
4.2 挖掘流程


1.1428571429·x2+0.0833333333·x3
0.4135366641·x2-0.001283055089·x3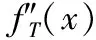



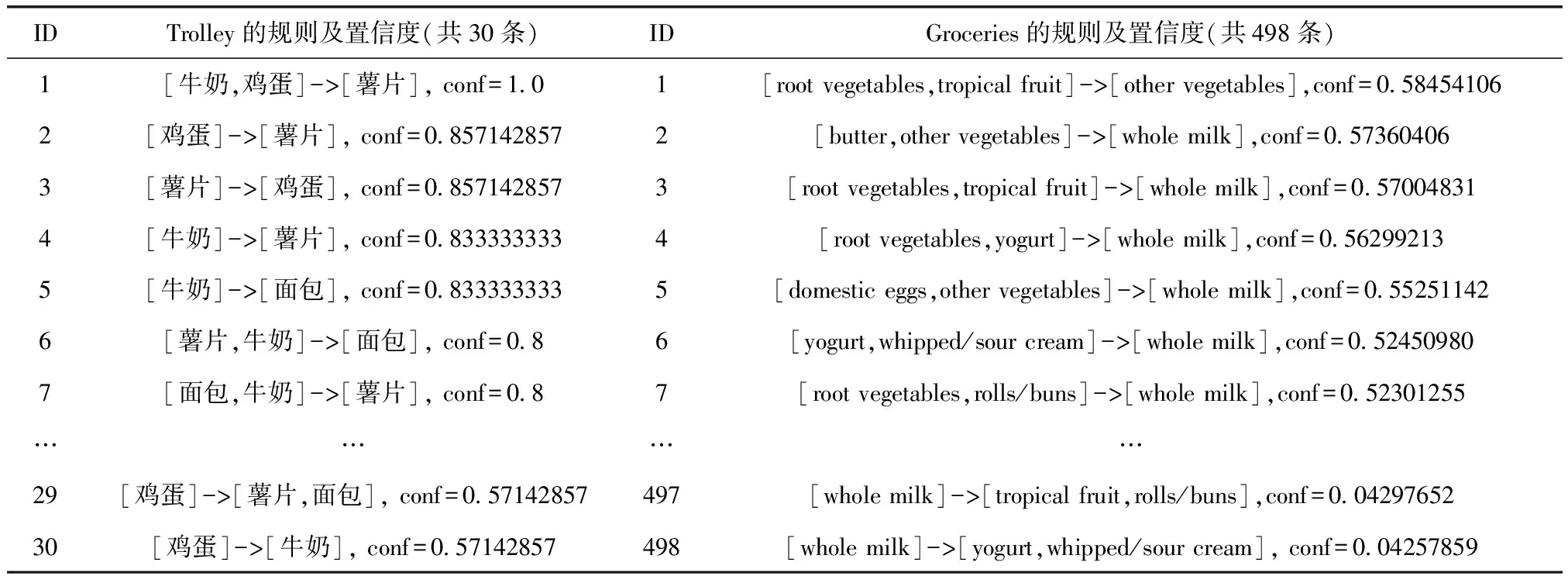
4.0050650021E-4·x2-5.6182859607E-6·x3
6.7022637026E-6·x2-6.426271112E-9·x3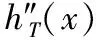

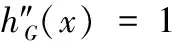

4.3 结果分析与讨论
5 结束语
