加筋板极限强度数值计算影响因素及敏感分析❋
2018-12-22王保森甄春博
王保森, 董 胜, 冯 亮, 甄春博
(1.中国海洋大学工程学院,山东 青岛 266100; 2.威海海洋职业学院, 山东 荣成 264300; 3.大连海事大学, 辽宁 大连 116026)
加筋板极限强度数值计算影响因素及敏感分析❋
王保森1,2, 董 胜1, 冯 亮1, 甄春博3
(1.中国海洋大学工程学院,山东 青岛 266100; 2.威海海洋职业学院, 山东 荣成 264300; 3.大连海事大学, 辽宁 大连 116026)
船用加筋板极限强的有限元计算方法应用广泛,但其计算方法具有一定的不稳定性,计算结果受多种因素的影响。本文针对加筋板有限元计算方法的不稳定性进行研究,通过将有限元计算结果与其他学者的研究成果进行对比,验证了本文所采用的有限元方法的可靠性,然后针对加筋板材料、边界条件、网格密度、初始缺陷等几种因素的敏感性进行了具体的研究,发现使用材料的理想应力应变关系得到的计算结果偏于危险,且误差最大可达到17%左右,网格的形状和疏密程度对结果均有影响,边界条件若不考虑横向加强构件的作用,所得计算结果不准确,初始缺陷对有限元结果影响复杂,需要根据加筋板的实际缺陷选取适合的屈曲模态。
加筋板;极限强度 ;限元方法;影响因素;敏感分析;
加筋板是船体等的基本结构,在受到压缩、剪切、弯曲、扭转等荷载作用时,常因发生屈曲失稳而破坏。加筋板在受轴向压缩荷载作用时,其失稳过程一般包括两个阶段,即初始屈曲变形阶段和后屈曲变形阶段。加筋板达到的极限承载状态发生在后屈曲阶段,因此,准确地研究加筋板后屈曲阶段的承载力曲线对于研究加筋板极限承载力有重要意义。
利用有限元方法可以较好地捕捉到加筋板的后屈曲路径,得到极限强度的数值解。许多学者对有限元方法进行了深入研究,Fujikubo等[1]采用有限元方法研究了连续加筋板在受轴向压力和侧向压力作用下的极限强度,并基于有限元结果得到了复杂荷载作用下加筋板极限强度的解析公式。Paik等[2-4]采用ANSYS有限元分析(FEA)、DNV PULS、ALPS/ULSAP方法分别对无加强筋板和有加强筋板在双轴向压力和侧向压力作用下的极限强度进行研究,并对这几种方法的精确性进行了比较,提出有限元方法的初始缺陷形状、边界条件及荷载情况对计算结果均有影响。Zhang和Khan[5]用半解析公式法和有限元方法对轴压作用下加筋板极限强度进行了计算,列出了其中7种加筋板模型的计算结果,两种结果符合较好,并与其他学者的研究成果进行了比对。文献[6-14]从加筋板的模型、初屈曲模态、后屈曲特性等方面对加筋板极限强度产生的影响进行了分析,说明这些方面对加筋板极限强度结果具有不同程度的影响。
本文采用非线性有限元分析方法,计算文献[5]中列出7种加筋板模型受轴向压力作用下的极限强度,并将计算结果与文献[5]结果及其他学者的理论结果进行比对,然后分别考虑加筋板材料、边界条件、模型网格密度、初始缺陷等敏感因素对该有限元方法计算结果的影响,给出具体的误差结果。
1 非线性有限元分析方法
1.1 有限元模型
本文采用能对加筋板非线性屈曲问题进行有效分析的Riks弧长法,该方法是目前结构非线性分析中稳定高效的迭代控制方法之一,原理是通过牛顿—拉夫逊法在求解过程中同时控制荷载因子和位移增量的步长,有效的分析结构非线性前后屈曲并跟踪后屈曲路径。在有限元软件中利用该方法对文献[5]中的7种不同尺寸的加筋板模型进行极限强度计算,模型尺寸如表1所示,其中a表示两横档之间的长度,b表示加强筋的间距,t表示板的厚度,hw表示加强筋腹板的高度,tw表示加强筋腹板的厚度,hf表示翼板的宽度,tf代表翼板厚度。
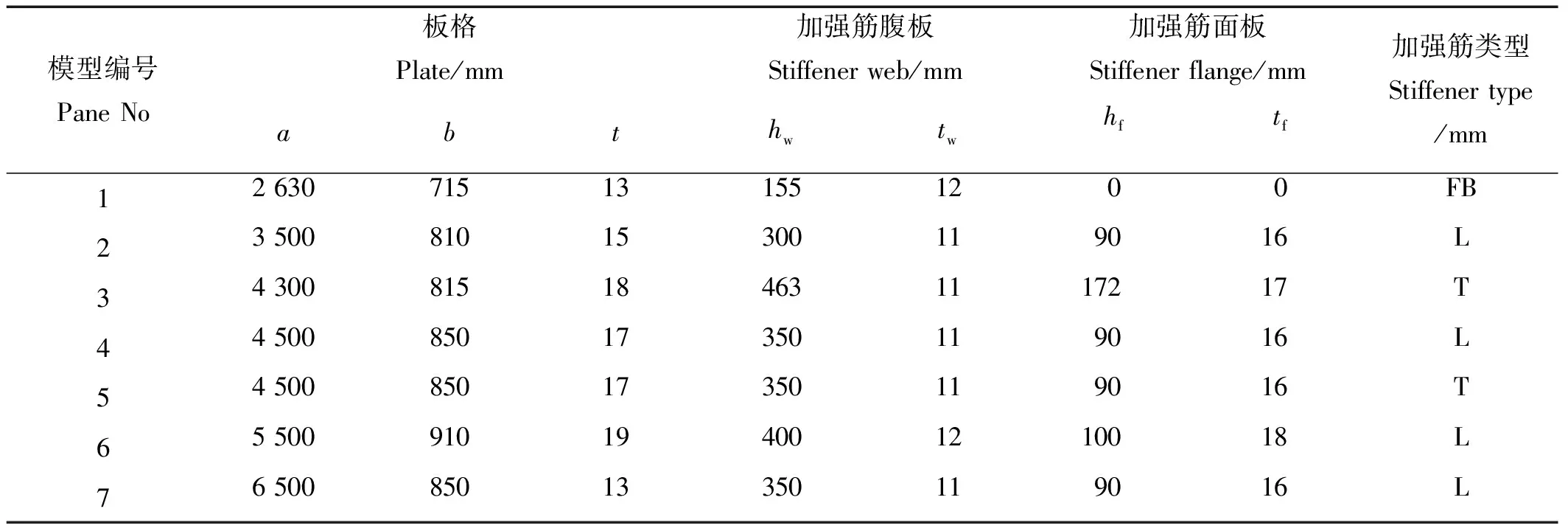
表1 7种典型船舶加筋板的尺寸Table1 Seven kinds of typical sizes of stiffened panels
为消除边界效应的影响,沿模型的纵向设置2档跨距a/2+a+a/2,沿横向设置10档加强筋。横框架在有限元模型中不建模,而采取在横框架处施加相应的约束条件进行模拟,整个加筋板结构均采用有限元软件中的shell单元进行模拟。加筋板有限元模型见图1。
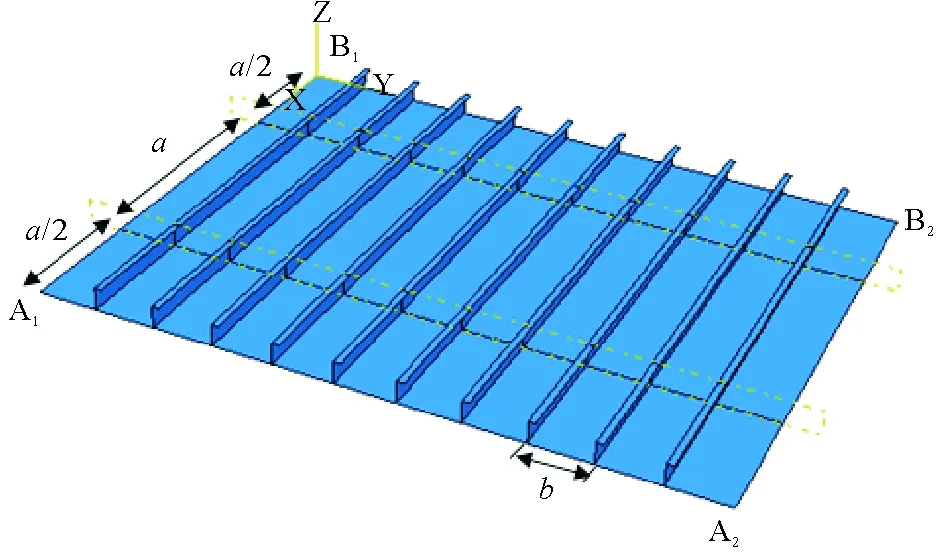
图1 加筋板有限元模型
模型材料采用HT32钢材,材料参数为:弹性模量为E=205 800 N/mm2,泊松比ν=0.3,比例极限σu=190.512 MPa,屈服极限为σs=340.2 MPa(据文献[16]该高强度钢材的屈服极限名义值为315 MPa,平均值为340.2 MPa)。
模型采用右手笛卡尔坐标系,坐标x和y在加筋板平面内,x轴与加强筋的方向平行,坐标轴z垂直于x、y轴所在平面,与加强筋的腹板方向平行。
单元类型均为四节点的四边形单元,板沿横向每档划分为6个单元,纵向单元数量合理选择以保证网格形状接近正方形,加强筋腹板高度划分为3个单元,加强筋面板宽度方向划分为2个单元。
约束A1~A2边及B1~B2边绕y轴及z轴的转动自由度;A1~B1及A2~B2边在z向固定,同时约束绕y轴及z轴的转动自由度;约束横框架所在处板的z向自由度,同时加强筋的腹板在此处保持垂直,以反映横框架的支撑作用;在A1~A2边及B1~B2边设置参考点,使A1~A2边及B1~B2边沿x轴方向具有相同的位移。
1.2 有限元计算结果
采用有限元法首先对加筋板模型进行特征值屈曲分析,然后将分析结果作为初始缺陷引入到后屈曲分析中,使用有限元软件提供的修正的弧长法(STATIC,RIKS)计算得到加筋板受沿纵向轴压力作用下的加筋板极限强度,图2、3分别为加筋板受纵向轴压的变形结果与加筋板沿纵向所受的平均压力和相应的位移关系曲线。

图2 加筋板受纵向轴压的变形结果Fig.2 Deformation results of stiffened plate subjected to axial compression
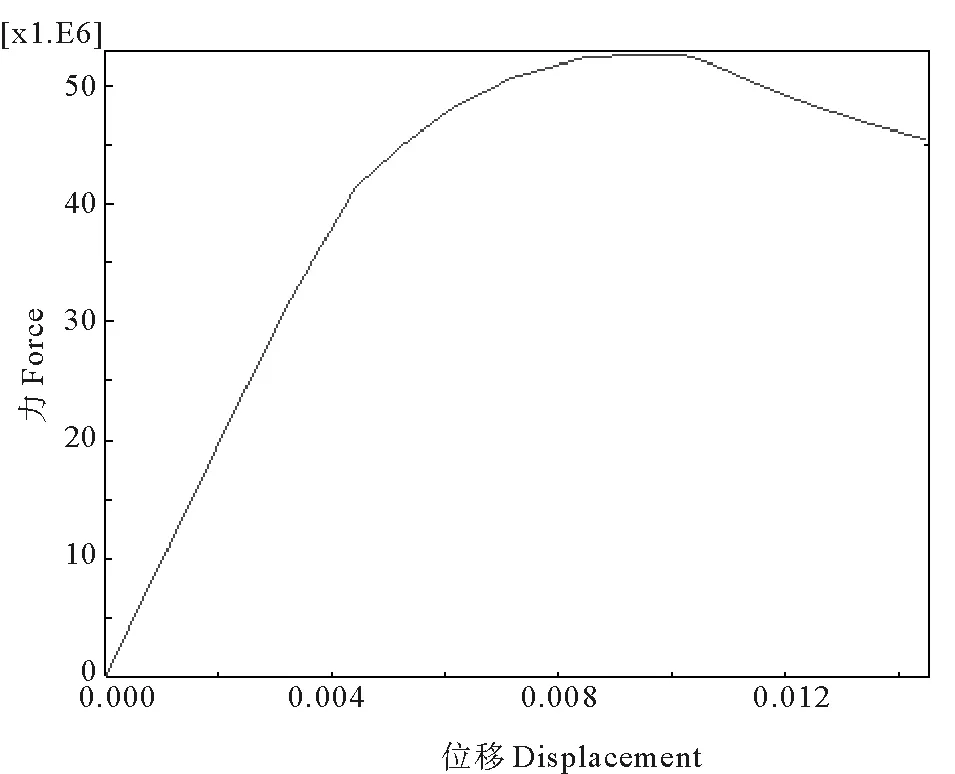
图3 平均力-位移曲线图
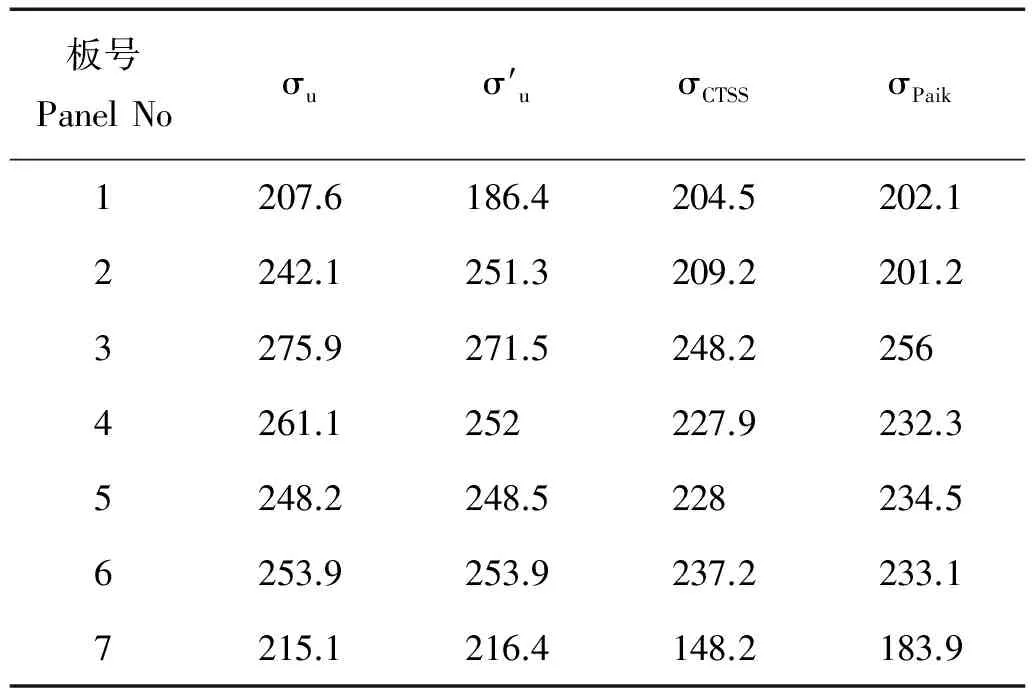
表2 加筋板极限强度的有限元结果和理论公式结果比较Table 2 Comparison of ultimate strength of stiffened plate of finite element calculation and theoretical calculation /MPa
σu(CTSS)是文献[15]中推导的理论公式计算结果,其理论公式表达式如下:
(1)
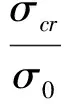
σu(Paik)是文献[7]中经验公式计算结果,计算公式如下:
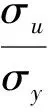
0.188λ2β2-0.067λ4)-0.5。
将本文有限元法结果σu与σu(CTSS)和σu(Paik)进行比较,可以看出模型7计算结果差距较大,约为20%,这是由于加筋板属于组合结构,很多误差在计算时会形成累积,故理论公式方法在计算结果上有些偏差。但这几种算法的趋势是一致的,总体来说有较好的吻合程度。
2 有限元敏感因素分析
2.1 加筋板材料分析
材料的理想应力-应变关系可根据线性定律和理想弹塑性假设求得,但对于非线性较大的钢材来说,其理想应力-应变关系与实际相比存在较大误差,通过文献[16]给出的HT32钢材的拉伸试验数据可以得到它的真实应力-应变关系。
为研究材料的应力-应变关系对有限元结果的影响,分别取材料的真实塑性应力-应变关系与理想应力-应变关系进行对比研究,真实应力-应变关系与理想应力-应变关系如下图4所示,从图中可以看出真实应力-应变关系除了直线段,还具有一段明显的非线性段。两条曲线均在曲率达到零之后保持水平,即材料应力大小保持不变,应变值继续增大,说明此时达到了材料的屈服极限。
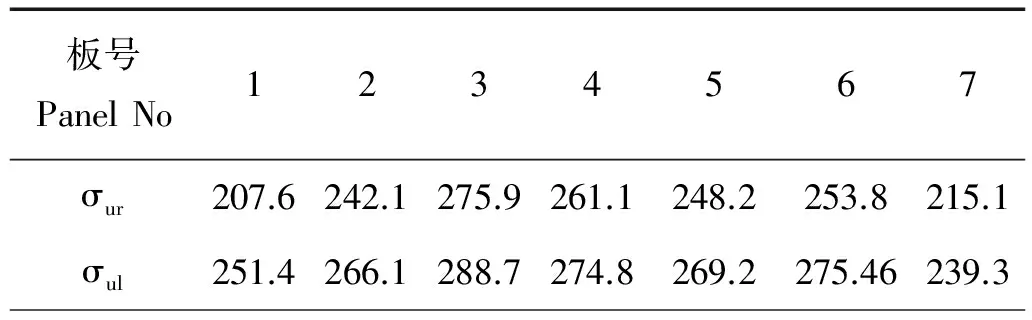
采用上述两种应力-应变关系的计算结果如下表3所示,其中σu是采用材料的真实应力-应变关系计算所得结果,σul是理想应力-应变计算结果。
由表3的计算结果可以看出用材料理想应力-应变计算结果比真实应力-应变计算结果偏大,最大差距可达到17.4%,最小在5%左右,说明应力-应变关系对有限元结果精度具有较大影响,采用真实应力-应变关系计算精度较好,而用理想应力-应变关系计算结果偏危险。

图4 材料真实塑性应力-应变与理想应力-应变曲线Fig. 4 True stress-strain curve and the ideal stress-strain curve of plastic material
2.2 边界条件分析
根据船舶加筋板结构的对称性及实际受力特点,其边界可设置为简支边界条件,横向加强构件对加筋板有一定的支撑作用,在有限元模型中可以不对横向加强构件进行建模,采用约束板格竖向的位移与加强筋横向位移的方法进行替代,为研究此横向边界对有限元结果的影响,本文分别选取文献[5]提供的1/2+1+1/2模型(模型一),相邻强横梁之间的加筋板(模型二),以及简化分析模型1/2+1/2(模型三)如图5(a)、(b)、(c)所示,分析不同边界条件对模型计算结果的影响。

图5 三种边界条件的数值模型
表4中σu1、σu2、σu3分别是模型一、二、三的计算结果,从计算结果来看模型一与模型三的计算结果基本一致,最大误差为3.4%,模型二计算结果误差达到约7%,且数值计算过程中存在不收敛问题,说明考虑横向强力构件在边界条件中的作用得到的计算结果较为准确,若忽略横向加强构件的支撑作用,可能会造成局部板或加强筋的过早屈曲,而使极限强度偏离真实值。
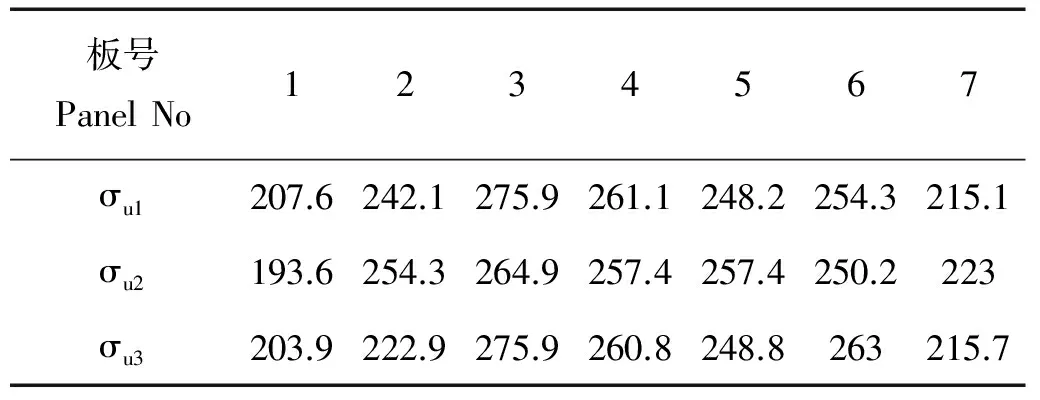
表4 三种边界条件下的模型数值计算结果Table 4 Numerical results of the model under three boundary conditions /MPa
2.3 网格密度分析
本文为探讨有限元模型网格密度对计算结果的影响,首先将模型划分成粗糙的网格,为研究方便采用简化分析模型1/2+1/2,板单元网格划分情况和数值计算结果如表5所示。
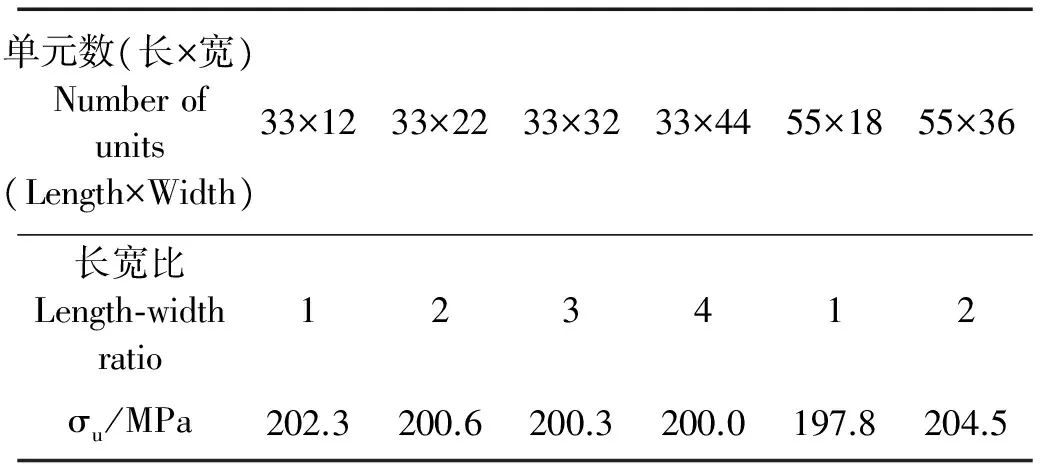
表5 不同网格密度下加筋板数值计算结果Table 5 Numerical results of stiffened plates with different mesh densities
由表5计算结果看出采用不同长宽比网格的计算结果出现了3.4%的误差,随网格密度和单元长宽增大,极限强度值有减小趋势,但也看出并非网格越密,极限强度越小,在加密网格且长度单元数不变时,沿宽度方向加密网格,计算结果相应减小,单元长宽比从1到4误差为1%左右。
为进一步研究网格密度对数值计算结果的影响,需要考虑屈曲挠度的大小,遵循在一个半屈曲波长内至少要跨越5个单元的原则,将模型的网格划分为如图6中(d)、(e)所示的两种情况:
网格模型1 板沿横向每档划分为6个单元,合理选择纵向单元数量以保证网格形状接近正方形,加强筋腹板高度划分为3个单元,加强筋面板宽度方向划分为2个单元,模型节点数2 340个,单元数2 262个。
网格模型2 板沿横向每档划分为12个单元,合理选择纵向单元数量以保证网格形状接近正方形,加强筋腹板高度划分为6个单元,加强筋面板宽度方向划分为4个单元,模型节点数9 087个,单元数8 932个。
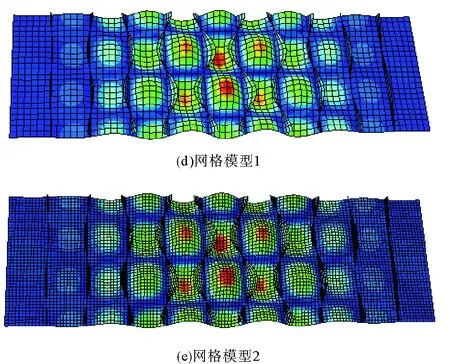
图6 两种网格模型屈曲模态Fig. 6 Two kinds of buckling mesh model
对这两种不同网格密度的模型进行屈曲计算,屈曲变形结果如图6所示,得到网格模型1屈曲因子特征为0.13486,极限强度计算结果为203.9 MPa,网格模型2屈曲因子特征为0.129 76,极限强度计算结果为200.9 MPa,误差为1.4%,为得到普遍的规律,分别将7种加筋板模型网格加密一倍,数值结果如表6所示。

表6 两种网格模型数值计算结果Table 6 Two numerical results of kinds of mesh models /MPa
从表6中计算结果可以看出,将有限元网格划分为正方形且将网格密度提高一倍,计算结果均有减小,最大差距在3%左右,此时网格密度对计算结果影响较小。
2.4 初始缺陷分析
在用非线性有限元计算加筋板的极限强度时,为使数值模拟过程与计算结果更符合实际,需要考虑初始缺陷的影响,即在有限元模拟中需要将屈曲屈曲模态引入到后屈曲分析中,由于低阶模态相比高阶模态具有更小的应变能,结构更有可能按照低阶模态的形状变形,一般选择低阶模态作为初始缺陷,比例因子一般取板长的1/1 000,文献[6]中列出了几个初始缺陷ωmax的计算公式,按大小分为三个量级,计算公式如下:
ω1=0.025tβ2,
(2)
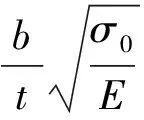
(3)
ω2=0.005b,
(4)
ω3=0.3tβ2,
(5)
式中:β为细长比;t为板的厚度;b为加强筋之间的宽度;σ0为加筋板极限强度;E为弹性模量。
由于屈曲模态和比例因子两个因素共同影响数值计算结果,为便于分析两种因素对数值计算结果的影响,采用控制变量法分别对其进行研究。
2.4.1 屈曲模态 为研究各阶模态对数值计算结果的敏感性,选择其中一个加筋板模型进行屈曲模态分析,取前10阶模态依次加到后屈曲分析中,比例因子均取板长的1/1 000,计算结果见表7。

表7 前10阶屈曲模态数值计算结果Table 7 Numerical results of the first 10 order buckling modes
由表7计算结果看,各阶屈曲模态得到的计算结果差距较小,误差最大为3%,8、9、10模态计算结果与1阶模态结果几乎相同,说明引入单阶模态计算结果以低阶模态结果为主。
图7、8分别为1阶屈曲模态和相应的变形结果,图9、10为9阶屈曲模态和相应的变形结果,可以看出两个模态的变形结果基本一致,均与1阶屈曲模态相同,说明引入高阶屈曲模态计算变形会跳到低阶屈曲模态,从模型变形上验证了极限强度值趋近一致的现象。
2.4.2 比例因子 比例因子的作用是按照一定的比例将特征屈曲模态进行缩放,将缩放后的屈曲模态作为初始缺陷引入到后屈曲分析,为研究不同比例因子对有限元结果的影响,7种加筋板均选用1阶屈曲模态,比例因子分别取板长的1/1 000和据文献[6]公式(2)和(4)的计算值及公式(2)和(5)的平均值,对结果进行比较。
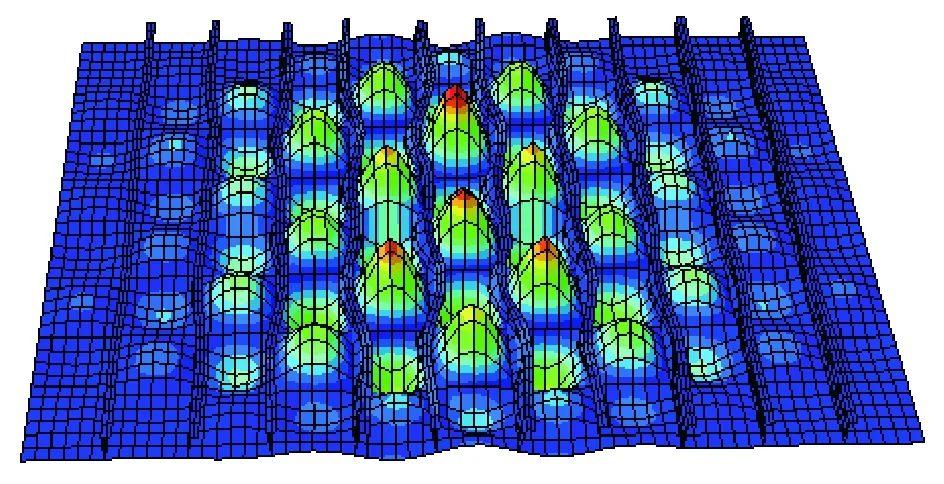
图7 1阶屈曲模态 Fig.7 1 order buckling mode
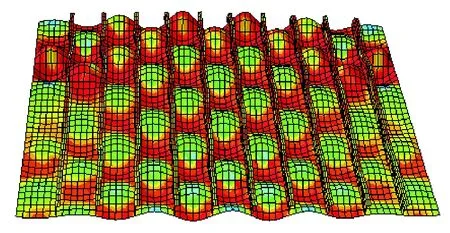
图8 后屈曲变形
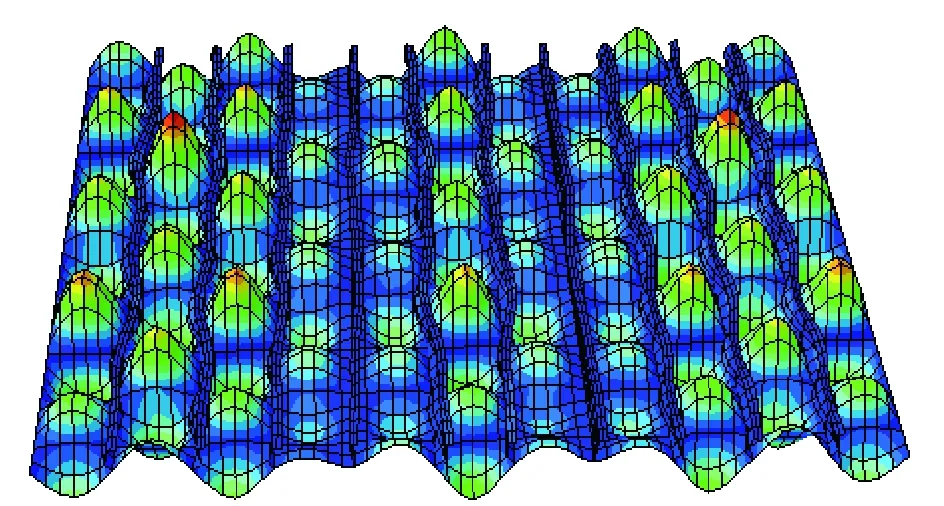
图9 9阶屈曲模态 Fig.9 9 order buckling mode

图10 后屈曲变形Fig.10 Post buckling deformation
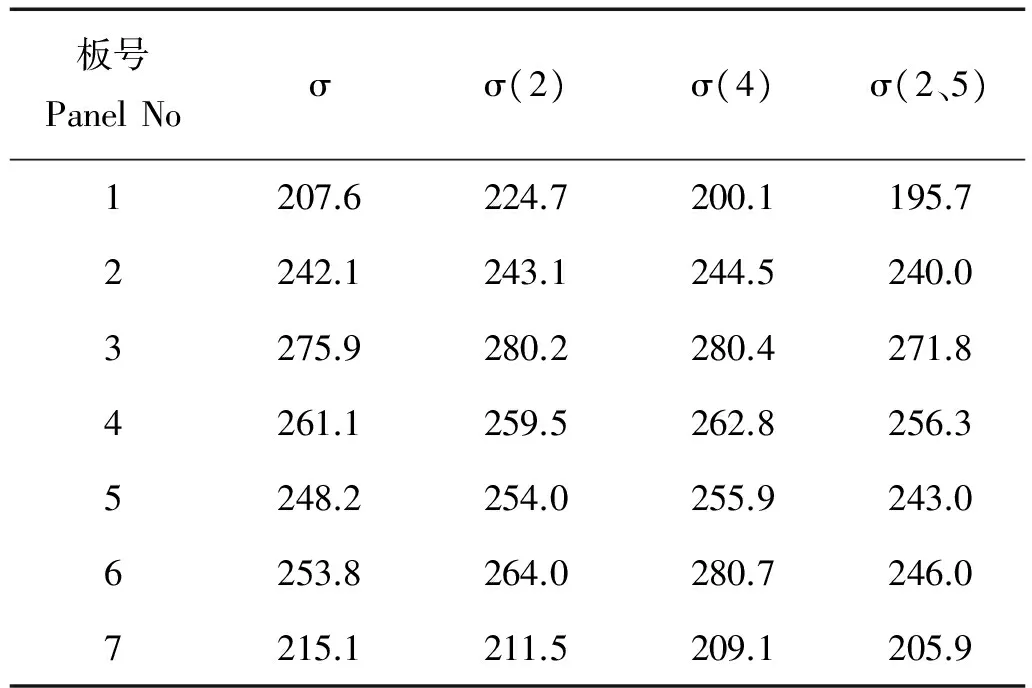
表8 四种不同比例因子数值计算结果Table 8 numerical results of four different scaling factors /MPa
由上表计算结果看,模型1比例因子取公式(3)的计算值1.6 mm,相对误差为8.2%,模型6比例因子取公式(5)的计算结果0.095 mm,相对误差达到10.6%,其余计算结果差距在5%以内,说明大部分模型的计算结果相差较小,但也出现了两个模型的误差达到了10%左右,这是由于比例因子的选取决定着初始缺陷的大小,其量级大小影响加筋板的初始变形情况,进而影响加筋板的的极限强度,可见比例因子是具有较大敏感性的影响因素。
为进一步研究屈曲模态和比例因子的共同作用对有数值计算结果的敏感性,将前5阶屈曲模态按1阶模态0.1%,2阶模态0.8%,3阶模态0.06%,4阶模态0.04%,5阶模态0.02%的方式进行叠加,将叠加后的结果作为初始缺陷引入后屈曲分析中,数值计算结果如表9所示,其中Ⅰ表示前5阶模态计算结果,Ⅱ表示2阶模态计算结果。
从表9中计算结果可以看出,引入前5阶屈曲模态的数值计算结果比只引入2阶模态的计算结果有1%~5%的减小,说明按此方式引入叠加模态的数值计算结果与单独引入2阶模态计算结果差距不大,2阶模态在此叠加模态中起主导作用。
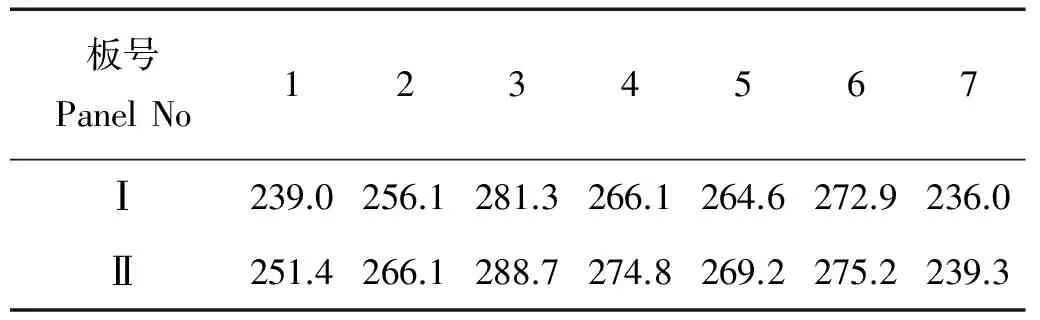
表9 两种屈曲模态计算结果Table 9 Calculation results of two kinds of buckling modes /MPa
总的来说,屈曲模态的选取要与实际情况相结合,选择合适的初始变形,有限元方法中通过模态叠加得到的变形结果需要以实际变形情况做参考,计算结果才更接近真实值。
3 结论
采用非线性限元法计算7种不同尺寸加筋板模型的极限强度,将可能对有限元结果产生影响的材料属性、网格密度、初始缺陷、边界条件等因素的敏感性进行了具体的分析得到以下结论:
(1)在有限元模型的材料属性中需要设置材料的应力-应变关系,本文分别采用材料的理想应力-应变关系和真实塑性应力-应变关系进行对比研究,发现采用理想应力-应变关系求得的极限强度值与材料的真实塑性应力-应变关系的计算值相比偏于危险,误差达到17%左右,是有限元方法中较敏感的因素。
(2)从模型一、模型三的计算结果来看,考虑横向边界条件的作用得到的计算结果较为准确,相比之下,模型二的计算结果有7%的误差,且存在不收敛问题,由此说明不能忽略横向边界条件对加筋板的支撑作用,否则会造成局部板或加强筋的过早屈曲,导致计算结果偏小。
(3)在粗糙网格下,将单元长宽比增大,极限强度值有减小趋势,若按一定原则将网格进行划分,即在一个半屈曲波长内至少要跨越5个单元,且板的网格接近正方形,在此原则下对网格加密一倍,对结果影响不大,敏感性较小。
(4)如果只把单阶特征屈曲模态的计算结果引入到后屈曲分析,得到的计算结果与1阶屈曲模态的计算结果差别不大,说明板的屈曲变形以低阶模态为主,敏感性较小。如果把前5阶特征屈曲模态的计算结果叠加到一起引入到后屈曲分析,得到的计算结果相比于1阶屈曲模态的计算结果有不同程度的减小,最大误差为5%,说明引入叠加模态对计算结果的敏感性高于单阶模态。
(5)按照不同标准选取的比例因子得到的计算结果之间差距达到了10%,说明比例因子的取值对计算结果具有较大的影响,敏感性较强,因此比例因子的取值应参考实验模型真实的初始缺陷进行选取。
[1] Fujikubo M, Yao T, Khedmati M R, et al. Estimation of ultimate strength of continuous stiffned panel under combined transverse thrust and lateral pressure Part 1: Continuous plate[J]. Marine Structures, 2005, 18(5-6): 383-410.
[2] Paik J K, Kim B J, Seo J K. Methods for ultimate limit state assessment of ships and ship-shaped offshore structures: Part I—Unstiffened plates[J]. Ocean Engineering, 2008, 35(2): 261-270.
[3] Paik J K, Kim B J, Seo J K. Methods for ultimate limit state assessment of ships and ship-shaped offshore structures: Part II stiffened panels[J]. Ocean Engineering, 2008, 35(2): 271-280.
[4] Paik J K, Seo J K. Nonlinear finite element method models for ultimate strength analysis of steel stiffened-plate structures under combined biaxial compression and lateral pressure actions—Part II: Stiffened panels[J]. Thin-Walled Structures, 2009, 47(8-9): 998-1007.
[5] Zhang S, Khan I. Buckling and ultimate capability of plates and stiffened panels in axial compression[J]. Marine Structures, 2009, 22(4): 791-808.
[6] Estefen T P, Estefen S F. Buckling propagation failure in semi-submersible platform columns[J]. Marine Structures, 2012, 28(1): 2-24.
[7] Paik J K, Thayamballi A K, Kim B J. Advanced ultimate strength formulations of ship Plating under combined biaxial compression/tension, edge shear, and lateral pressure loads [J]. Marine Technology, 2001, 38(1): 9-25.
[8] 施兴华, 杭岑, 嵇春艳. 带有初始缺陷船用加筋板极限强度的不确定性分析[J]. 工程力学, 2015(2): 221-226.
Shi Xinghua, Hang Cen, Ji Chunyan. Uncertainty in analyzing ultimate strength of ship stiffening plates with initial imperfections using nonlinear finite element methods[J]. Engineering Mechanics, 2015(2): 221-226.
[9] 万春华, 段世慧, 吴存利. 加筋结构后屈曲有限元建模方法研究[J]. 机械科学与技术, 2015(5): 795-798.
Wan Chunhua,Duan Shihui, Wu Cunli. Study on the Finite Element Modeling for Post-buckling Analysis of the Stiffened Structure[J]. Mechanical Science and Technology for Aerospace Engineering, 2015(5): 795-798.
[10] 王伟, 吴梵. 单根加筋板整体屈曲临界应力计算与分析[J]. 舰船科学技术, 2010, 32(10): 3-7.
Wang wei, Wu Fan. Calculating and analyzing of the overall buckling’s critical stress of single stiffened panels[J]. Ship Science and Technology, 2010, 32(10): 3-7.
[11] 徐荣章, 关志东, 刘璐. 屈曲模态对含缺陷复材加筋板后屈曲的影响[J]. 北京航空航天大学学报, 2014(9): 1299-1304.
Xu Rongzhang, Guan Zhidong, Liu lu. Effect of buckling mode on performance of post-buckled composite stringer-stiffened panels with debond[J]. J Beijing Univ Aeron Astron, 2014(9): 1299-1304.
[12] 杨帆, 岳珠峰, 李磊. 基于弧长法的加筋板后屈曲特性分析及试验[J]. 应用力学学报, 2015(1): 119-124.
Yang Fan, Yue Zhufeng, Li Lei. Analysis and experiment of post-buckling characteristics of stiffened panel under compress load by arc-length method[J]. Chin J Appl Mech, 2015(1): 119-124.
[13] 张婧, 施兴华, 顾学康. 具有初始缺陷的船体加筋板结构在复杂受力状态下的极限强度研究[J]. 中国造船, 2013(1): 60-70.
Zhang Jing, Shi Xinghua, Gu Xuekang. Ultimate strength study of stiffened plate under complex loading with initial imperfections [J]. Shipbuilding of China, 2013, 54(1):60-70.
[14] 张涛, 刘土光, 赵耀. 初始缺陷加筋板的屈曲与后屈曲分析[J]. 船舶力学,2003(1): 79-83.
Zhang Tao, Liu Shiguang, Zhao Yao. Buckling and postbuckling of imperfect stiffened plates [J]. Journal of Ship Mechanics,2003(1): 79-83.
[15] 冯亮, 佟福山. 基于强度稳定综合理论的加筋板极限强度分析[J]. 哈尔滨工程大学学报, 2011(12): 1539-1543.
Feng Liang, Tong Fushan. ultimate strength research of stiffened panels based on combined theory of strength and stability method [J]. Journal of Harbin Engineering University, 2011(12): 1539-1543.
[16] 雒高龙,张淑茳,任慧龙. 船用钢应力—应变关系的数学表达及其在计算加筋板屈曲应力中的应用[J].造船技术, 2006(3):13-18
Luo Gaolong, Zhang Shujiang, Ren Huilong, The mathematical expression of the ship's steel stress-strain relationship and its application in the calculation of buckling stress of reinforcement plate, 2006(3):13-18.
[17] 崔维成, 郑金鑫, 裴俊厚. 计及横向和垂向载荷影响的加筋板格有效板宽的理论计算方法[J]. 船舶力学, 2001(4): 20-25.
Cui Weicheng, Zheng Jinxin, Pei Junhou. An analytical method for calculating the effective width of stiffened panel plating considering the influences of transverse stresses and lateral load[J]. Journal of Ship Mechanics, 2001(4): 20-25.
InfluenceFactorsandSensitivityAnalysisofNumericalCalculationofStiffenedPanelUltimateStrength
WANG Bao-Sen1,2, DONG Sheng1, FENG Liang1,ZHEN Chun-Bo3
(1.College of Engineering, Ocean University of China, Qingdao 266100, China;2. Weihai Ocean Vocational College,Rongcheng 264300,China;3. Dalian Maritime University,Dalian 116026,China)
The stiffened plate is the basic structure of the hull, when it is subjected to compression, shear, bending, torsion, etc. often destroyed by buckling. When the stiffened plate is subjected to axial compression load, The instability process generally consists of two stages: the initial buckling deformation stage and the post-buckling deformation stage. The ultimate loading strength occurs in the post-buckling, Therefore, it is of great significance to study the bearing capacity curve of the buckling of stiffened plate. The finite element method of ship stiffened plate is widely used in marine structure design, but it is instable in some degree. Calculation results are influenced by many factors. In this paper, the instability of the finite element method is studied. the results of finite element method are compared with the results of other scholars. The reliability of the finite element method used in this paper is verified. Then, the sensitivities of several factors, such as the material parameters, the boundary conditions, the mesh density, and the initial defects, are studied. Many calculations is found, firstly, the ideal stress-strain relationship and the real stress-strain relation are studied in this paper, It is found that the ultimate strength value calculated by the ideal stress-strain relation is more dangerous than the calculated value of the real stress-strain relation, the error is about 17%, it is the more sensitive element in finite element method. Secondly, based on the calculation results of model 1 and model 3, the calculation results of lateral strength component in boundary conditions are more accurate, In comparison, the calculation result of model 2 is 7 % error, and there is no convergence problem, which indicates that the lateral boundary condition cannot be ignored to support the stiffened plate, Otherwise, the premature buckling of local plate or reinforcing rib will result in small calculation results. Thirdly, under the rough mesh, the width ratio of the unit is increased and the ultimate strength is decreased, If the mesh divided by a certain principle, at least five units in a half buckling wavelength,the mesh shape is close to the square, in this principle, the mesh is encrypted twice, which has little influence on the result and less sensitivity. Fourthly, the function of proportional factor is to scale the characteristic buckling mode according to certain ratio, post-buckling mode was introduced into the post-buckling analysis, the gap between the results was 10%. It is indicated that the value of proportional factor has a great influence on the calculation result, and its value should be selected according to actual size of imperfection by the experimental model.
stiffened panel; ultimate strength; finite element method; influence factor; sensitivity research
U661.43
A
1672-5174(2018)02-105-08
10.16441/j.cnki.hdxb.20150262
王保森, 董胜, 冯亮, 等. 加筋板极限强度数值计算影响因素及敏感分析[J]. 中国海洋大学学报(自然科学版), 2018, 48(2): 105-112.
WANG Bao-Sen, DONG Sheng, FENG Liang, et al. Influence Factors and Sensitivity Analysis of Numerical Calculation of Stiffened Panel Ultimate Strength[J]. Periodical of Ocean University of China, 2018, 48(2): 105-112.
上海交通大学海洋工程国家重点实验室开放基金项目(1404);山东省海洋工程重点实验室开放基金项目资助
Supported by State Key Labortory of Ocean Engineering, Shanghai Jiao Tong University(1404);Supported by Shandong Key Labortory of Ocean Engineering(201462010)
2015-04-15;
2016-06-20
王保森(1991-),男,硕士生。E-mail: wangbaosen91@163.com
❋ ❋ 通讯作者:E-mail: dongsh@ouc.edu.cn
责任编辑 陈呈超
