选煤厂钢结构-设备体系TMD振动控制研究

王 浩，丁北斗，李 雁，王 宁，米思奇

(1.国家网架及钢结构产品质量监督检验中心，江苏 徐州 221006；2.江苏省土木工程环境灾变与结构可靠性重点实验室,江苏 徐州 221116；3.徐州工程学院 土木工程学院，江苏 徐州 221018)

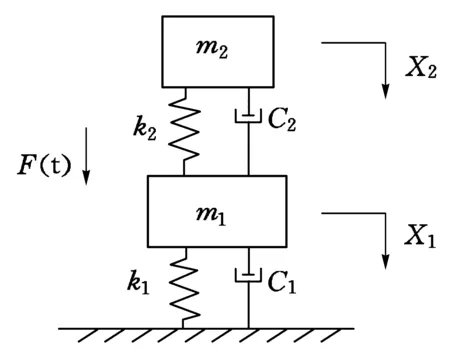
图1 TMD原理图

随着各种大型动力设备(如振动筛)的应用，其所产生的机械振动，会使新建或改造的工业厂房出现不同程度的结构振动问题，有的甚至出现了一些结构倒塌问题[1-2]，如“4·24孟加拉塌楼事故”就是由于该建筑中自备发电机产生的长期振动而引起的结构疲劳破坏，造成了重大的人员伤亡[3].然而，实际工程中所采用的增大构件截面尺寸、提高材料强度的常用加固方法，并未能很好地解决因动力设备振动引起的工业建筑的振动问题[4].调谐质量阻尼器(tuned mass damper,TMD)[5-6]是一种由质量、阻尼以及弹性元件组成的消能减振装置.它附属在主体结构上，可以通过可调谐的质量阻尼器吸收结构振动所产生的振动能量，有效减少主体结构的结构振动.其具有制作简单、灵活和高效的特点，被广泛应用于如钢结构和大型桥梁等土木工程中的振动控制[7-9].工业厂房振动问题，本质上是工业厂房随不同动力设备在卓越频率激励下的多阶动力谐响应问题，故而利用可以调谐的TMD调整结构与设备的共振频率，达到实现厂房减振效果[10].本研究基于TMD的结构-振动筛复合体系有限元分析，针对某选煤厂钢结构厂房由于振动筛工作时的振动引起楼板异常振动的问题，进行TMD参数以及TMD位置设计，实现了对该钢结构振动的有效控制.

1 TMD振动控制原理

TMD减振系统包括主结构和子结构(TMD)两部分，通过调整TMD的质量、阻尼、刚度参数对结构进行振动控制.TMD系统原理如图1所示.

1.1 主结构无阻尼时的TMD参数研究

在外荷载F(t)作用下，建立单自由度无阻尼结构(c1=0)，设置TMD的动力学方程[11-13]为：

(1)

(2)

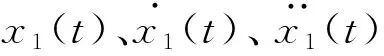
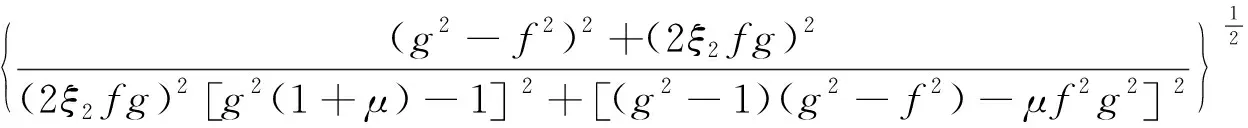
(3)

式中：g=ωn/ω1，为外激励荷载与主结构频率比；f为TMD结构与主结构频率比；μ为TMD结构与主结构质量比；ξ2为TMD阻尼比.根据式(3)，取质量比μ=0.05，固有频率比f=1.0，选择不同的TMD阻尼比，分别计算TMD阻尼比ξ2=0、ξ2=0.15、ξ2=0.35、ξ2为正无穷大时的主结构动力放大系数A(g).放大系数A(g)与频率比g之间的关系曲线见图2.

从图2可以看出：当TMD阻尼比取不同值时，动力放大系数与主结构频率比关系曲线总会存在A和B公共交点；阻尼比越小，峰值越大，随着阻尼比增大，峰值减小，但超过一定限值后，峰值又重新增加；当阻尼比在0.15～0.35时，动力放大系数为有限值.因此，根据动力放大系数和频率比关系曲线，可以得到结构体系在TMD作用下的最小动力放大系数，而此时对应的TMD阻尼比即为最优阻尼比ξopt.据计算可得最优固有频率比

(4)

则最优TMD阻尼比

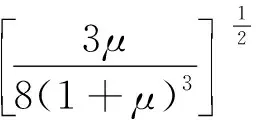
(5)

由公式(4)和式(5)可见，fopt和ξopt都与质量比μ有关，因此设计无阻尼TMD时，首先设定质量比μ，然后分别计算出TMD最优固有频率比fopt和最优阻尼比ξopt，再求解TMD的弹簧刚度、阻尼等结构参数.最优TMD参数下主结构动力放大系数变化曲线如图3所示.该方法又称之为Den Hartog法.

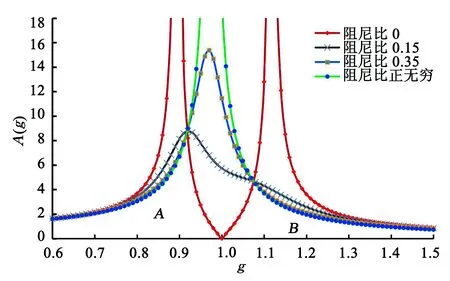
图2 动力放大系数A(g) 与频率比g关系曲线

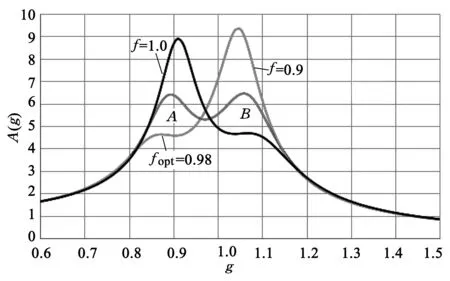
图3 最优TMD参数下结构 动力放大系数曲线

1.2 小阻尼主结构的TMD参数研究

当主结构有阻尼时，使用Den Hartog法并不方便，需要进行调整，即小阻尼主结构下TMD最优频率比和最优阻尼比的2个经验公式[14-15]为：

(6)

(7)

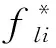
(8)

(9)

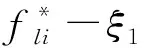
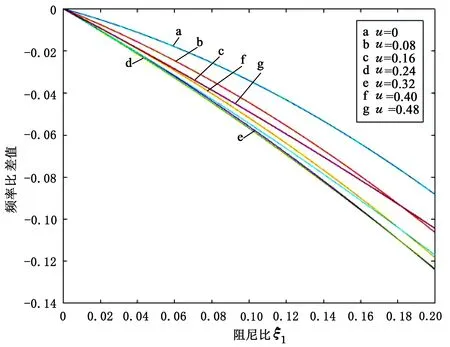
图曲线

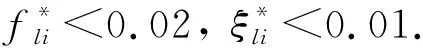
2 基于ANSYS有限元的结构动力分析

2.1 工程概况

某选煤厂主厂房及浮选车间为钢框架结构，楼板由压型钢板复合楼板而成，车间3层布置了4台振动筛.振动筛安装在3层楼面上.该层动力设备众多，振动筛等设备运行时引起楼板受迫振动明显.工作正式运行时发现：整个楼层振动幅度加大，尤其在振动筛310附近尤为厉害，连邻近的窗户都在晃动；地面也有较大幅度的波动；振动筛309附近，有混凝土断裂现象，如图6所示.

图6 309振动筛前的地板裂缝(运行时振动幅度较大)

2.2 有限元建模

依据现场测试结果和图纸资料，进行有限元建模，并根据结构异常振动的引起原因，对3层4台振动进行简化建模.如图7、图8所示.

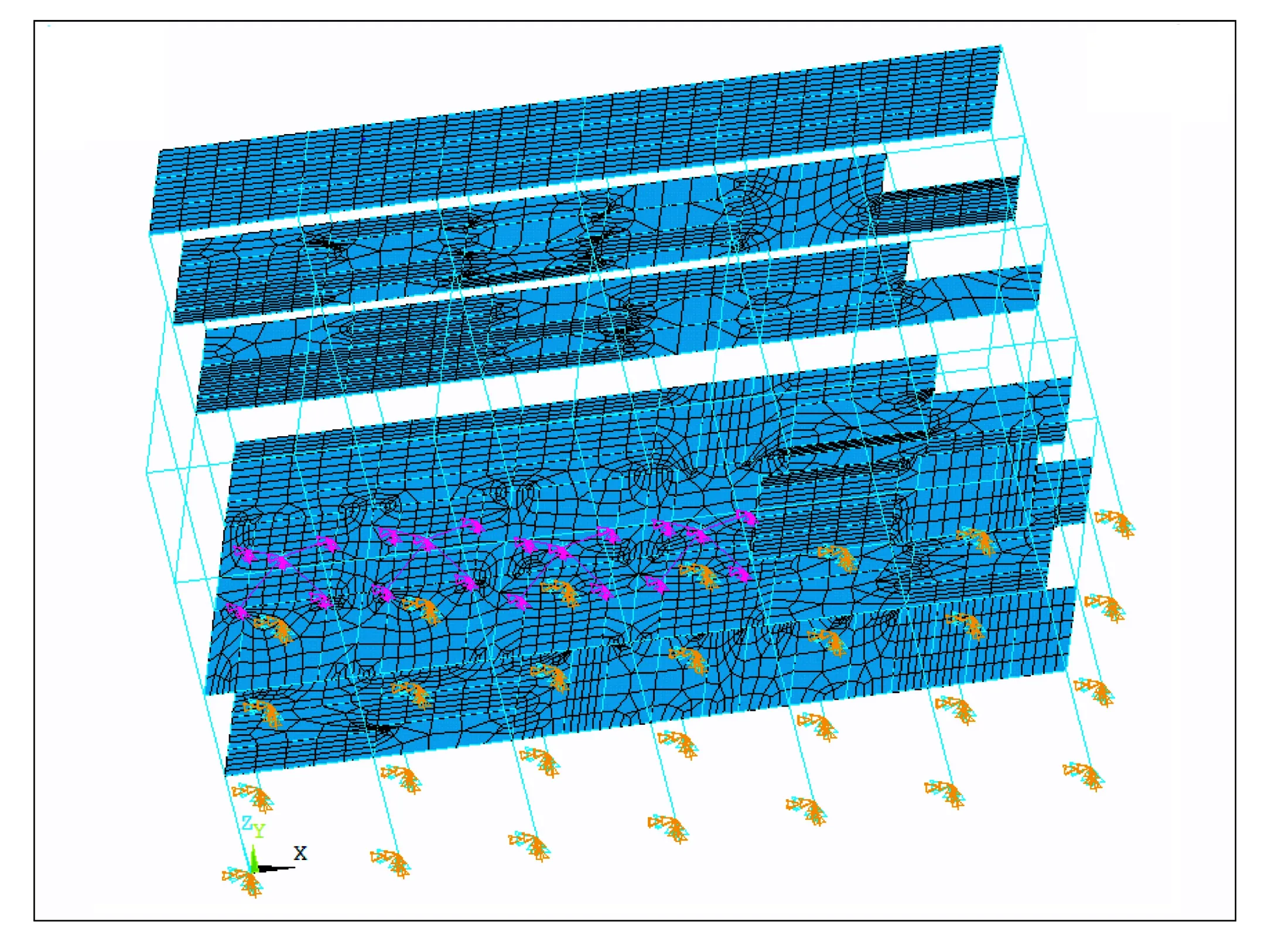
图7 选煤厂整体结构有限元模型

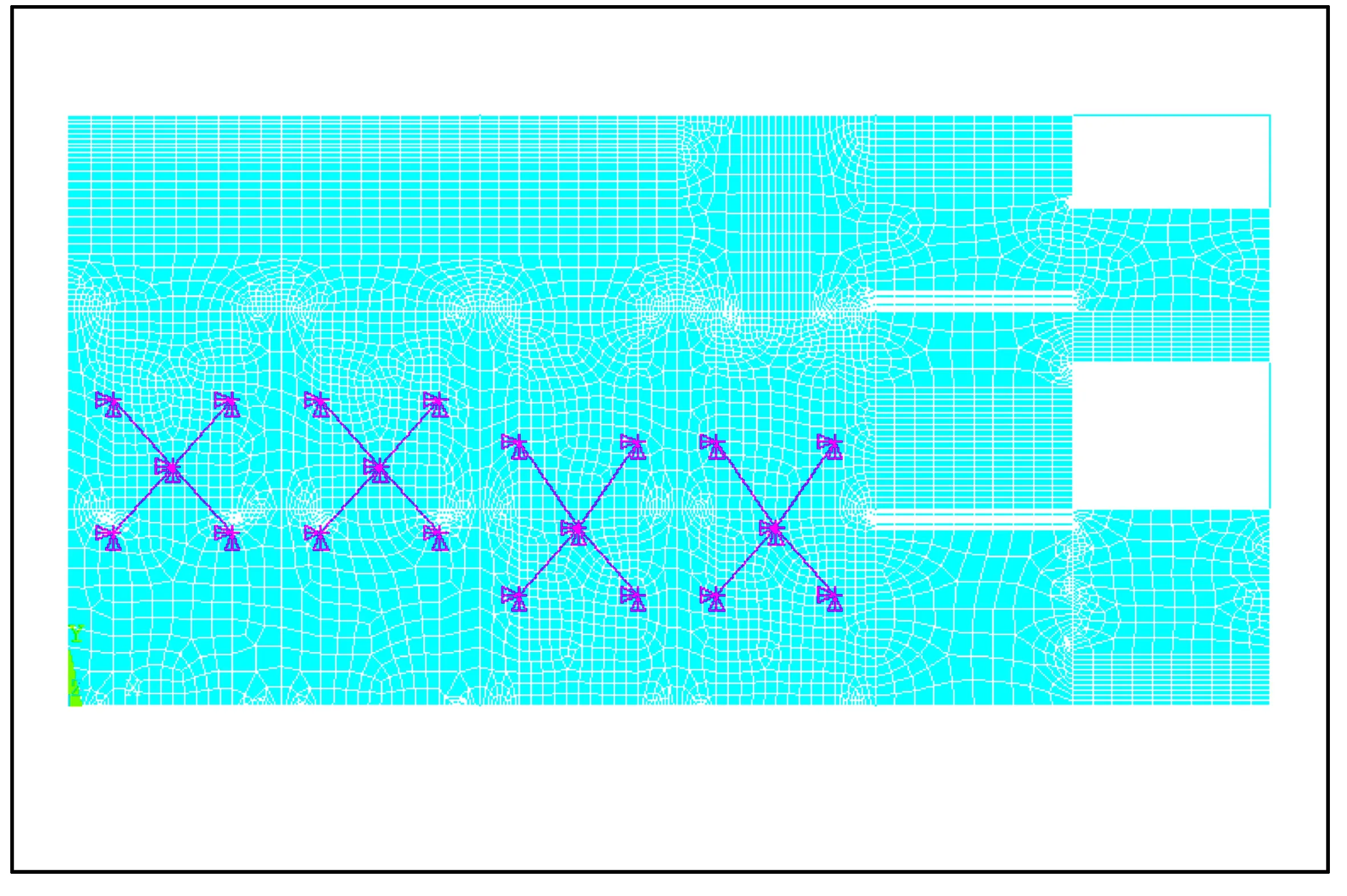
图8 9.7 m楼板处选煤厂局部结构有限元模型

2.3 TMD参数设计

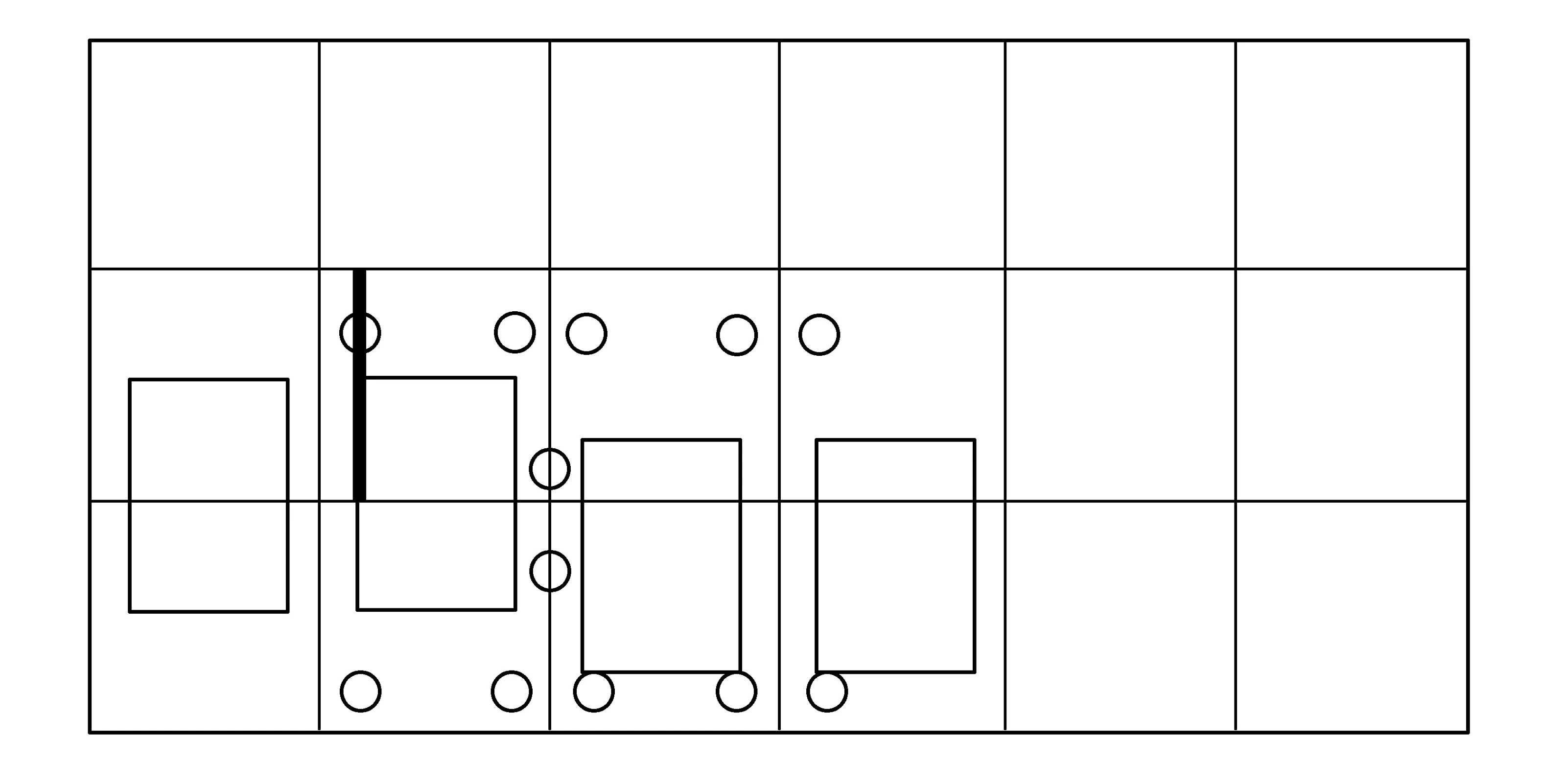
图9 TMD分布图

基于ANSYS有限元，模拟得到选煤厂结构总质量约为1 240 t；设定TMD质量与选煤厂结构的质量比μ=0.06；本次TMD总质量约取74.4 t，用12个TMD进行模拟.选煤厂阻尼比ξ1=0.03，根据Den Hartog经验公式，得到TMD与结构最优固有频率比fopt=0.943，TMD的最优阻尼比ξopt=0.15.TMD布置情况见图9.

2.4 结构谐响应分析

根据技术资料计算，每台振动筛的质量均为22.5 t，振动筛电机转速为950 r/min，振动筛扰力为Pz=23 620 N.选取典型区域节点，如振动筛支座附近处、楼板处节点进行分析.振动筛支座和楼板处所选节点分布如图10所示， TMD振动控制前后各节点位移频率变化如图11(图中的Uz、f分别表示节点峰值和位移)所示，TMD减振前后节点位移峰值变化见表1.

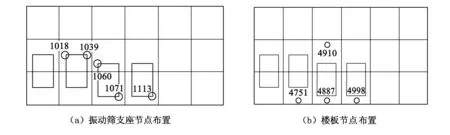
图10 振动筛支座和楼板上的节点分布图

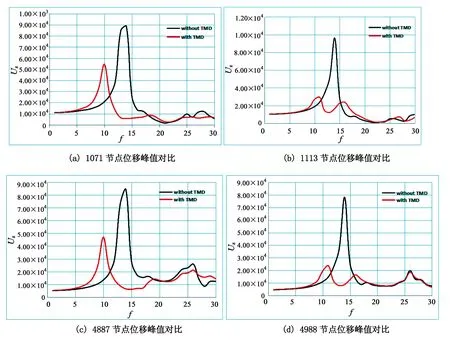
图11 TMD振动控制前后各节点位移频率变化图

节点号1018103910711060111315151504减小率0.4830.4390.3820.7260.6880.1380.125节点号1843185315724988488747514910减小率0.50000.2330.6960.4470.6170.393

从图11和表1可以看出：大部分节点振动响应得以大幅减弱， TMD装置减振效果明显；基本减振幅度在±50%； 1060、1113号节点处振动响应减弱了大约70%，原峰值处的频率降低为大约10 Hz，避开了共振区间.显然，对该结构的减振效果明显，结构安全得到保证.

2.5 结构瞬态响应分析

针对性地分别选取振动筛临近的支座、支撑梁及楼板，基于ANSYS进行有限元瞬态分析.节点分布如图12所示，TMD减振前后节点加速度瞬态分析对比如图13所示，TMD减振前后节点加速度响应对比见表2.根据图13和表2的节点加速度响应对比结果可知：减振前图像完全包含了减振后的时程曲线，节点的加速度响应相比减振前明显减小；大部分节点加速度减小幅值>50%；在4910号节点及其附近区域，达到最大值，即减小率为81.3%；梁上和楼板上节点加速度响应减少相对较低，如楼板4798号节点减振后为1.5 m/s2，虽然高于日本烟中元弘归纳的建筑物振动允许界限中安全范围(1.02 m/s2)，但也减小了大约26%，所以此时结构的振动处于安全合理状态.

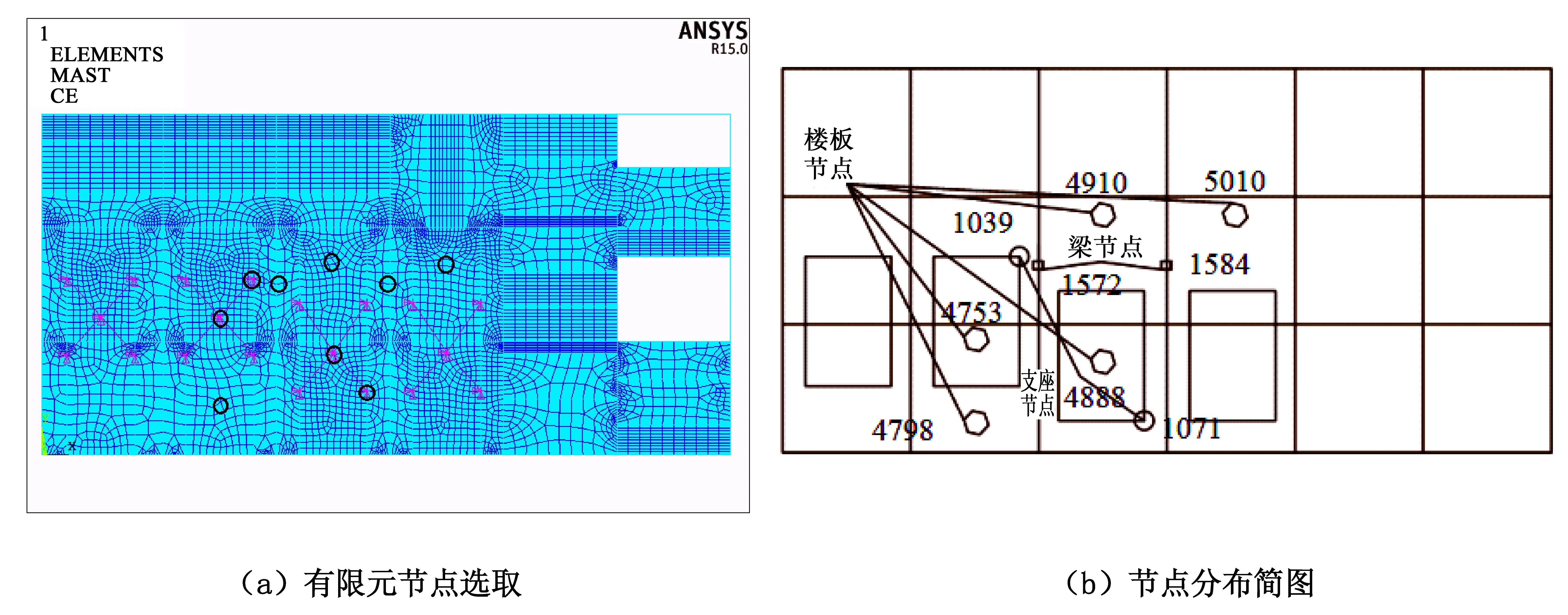
图12 瞬态分析节点分布图

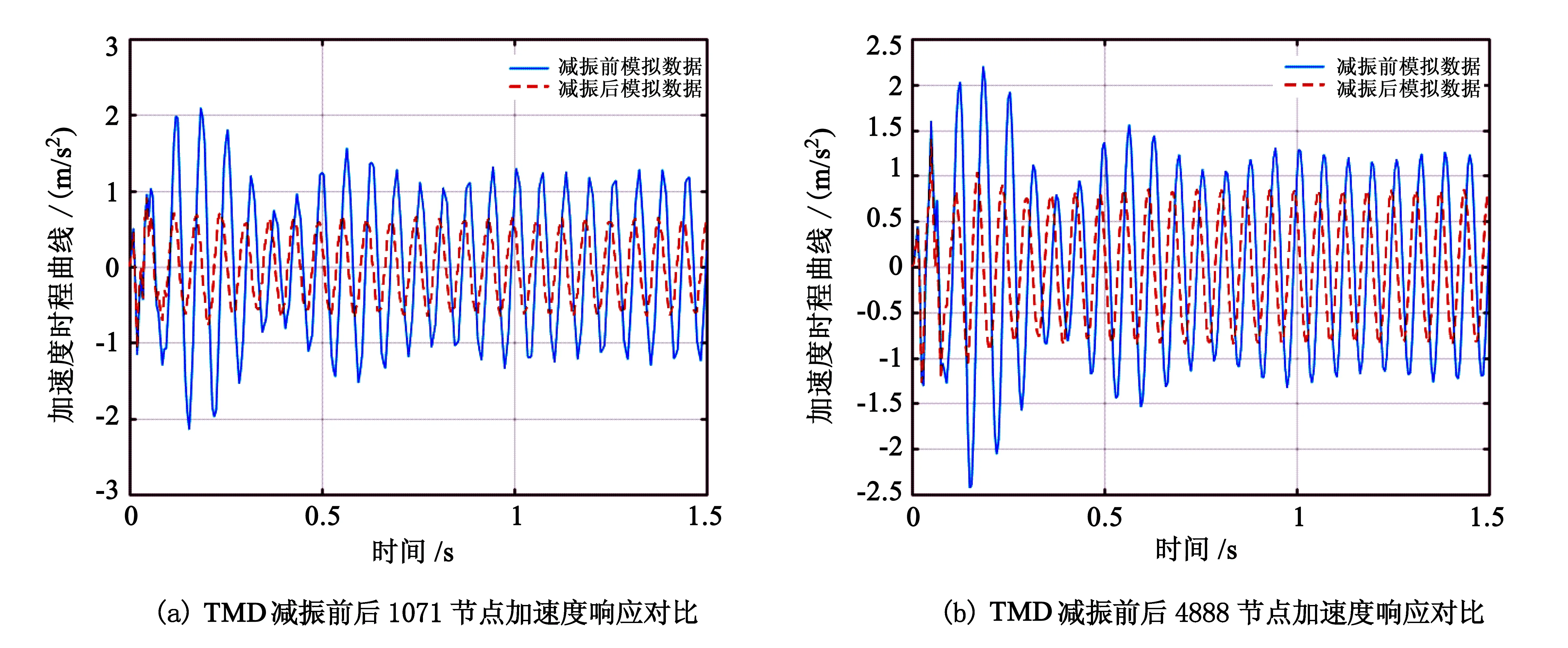
图13 TMD减振前后节点加速度瞬态分析对比图

节点号103910711584157250104910475348884798减小率0.5350.5310.5000.5690.5000.8130.4230.3330.260

3 结语

针对大型振动筛引起选煤厂厂房钢结构振动问题，以TMD系统对该结构进行振动控制.有限元分析结果表明：减振后位移峰值明显下降，对应加速度响应基本减弱幅度>50%，且减振前曲线基本包含了减振后时程曲线；TMD减振前后的楼板节点位移、加速度、速度响应与相关国内外规范比较，均减小到规定限值内，即最大位移减小约72.6%，其峰值所在频率约为10 Hz，从而避开了结构设备共振频率区域，实现了减振目标.