基于动态规划法对滚珠螺旋作动器电液控制系统进行冗余可靠度优化

曾 励,竺志大,张 帆,戴 敏,杨 坚

(扬州大学 机械工程学院,江苏 扬州 225127)

作动器用于航空飞行器，驱动升降翼，前、后缘襟翼，方向舵，水平尾翼以及舰载机的折翼等.随着高性能歼击机、舰载机、航天飞机的发展，对于旋转作动器不断提出新的要求，如需要输出的力矩更大，质量更轻等，促使旋转作动器技术不断发展，对其可靠性的要求就显得更为重要.要提高或改善作动器系统的可靠性，可以从两方面去考虑：1)通过提高零部件的可靠性来提高系统的可靠性；2)通过对作动器系统的零部件或子系统进行冗余配置，以提高系统各级子系统的可靠性.提高作动器系统零部件的可靠性应从其原材料的质量和制造工艺，以及对零部件的设计水平等多方面考虑，但往往是资源耗费巨大且收效也不理想.对可靠性要求极高的许多复杂系统，单靠通过改进零部件材料质量或制造工艺来提高可靠性是不够的.所以，为了使作动器系统达到高可靠性，除提高零部件的可靠性外，通常还配置冗余零部件或子系统，使作动器系统可靠性达到设计要求.然而，零部件或子系统的冗余配置，将使系统在费用、质量以及体积等方面付出较大的“代价”[1].为此，在对滚珠螺旋作动器系统进行可靠性设计时，应基于满足系统资源的要求对其进行可靠性冗余优化设计.

1 作动器系统可靠性的基本模型

1.1 零部件或子系统串联可靠性模型

串联系统特点是在一个系统中，若任何一个单元失效就可导致系统失效；或者是全部单元都能正常工作时，系统才能正常工作.通常情况下，机械系统都是以串联系统为主，其可靠性控制模型[2]如图1所示.

图1 串联系统的可靠性模型框图

若组成系统的n个单元(子系统或零部件)的可靠度分别为Ri(i=1,2,…,n,n为系统所包含子系统或零部件单元的个数)，则由独立失效的子系统或零部件单元构成的串联系统可靠度为

(1)

由式(1)可知，构成系统子系统或零部件的单元数越多，其系统失效概率就越高，因此，系统的可靠度就越低.

1.2 并联系统可靠性模型

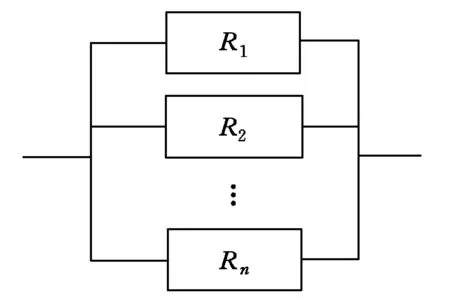
图2 并联系统可靠性模型框图

由子系统或零部件单元组成的并联系统如图2所示.组成并联系统的n个子系统或零部件单元中，若有一个子系统或零部件单元不失效，则整个系统就不会失效；或者说，全部n个单元的子系统或零部件都失效时，整体系统才能失效.设由子系统或零部件组成的n个单元的可靠度分别为Ri(i=1,2,…,n,n为系统所包含子系统或零部件单元的个数)，则由独立失效的子系统或零部件单元构成的并联系统可靠度

(2)

由式(2)可见，并联系统的总可靠度大于系统中任何一个单元的可靠度.在系统中若采用并联结构，将会使系统的尺寸、质量、价格等资源明显增加.一般通过并联方式对系统进行冗余或储备设计.

1.3 串-并联系统可靠性模型

串-并联系统即先并联后串联的系统，其可靠性模型框图如图3所示.该系统主要由并联子系统或零部件构成串联的整体系统.在计算系统的可靠度时，可先将并联的各子系统或零部件等效成各个单元，然后把整个系统看成一个串联系统来计算.

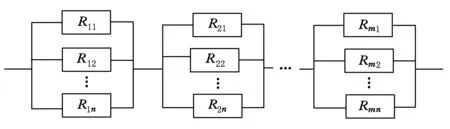
图3 串-并系统的可靠性模型框图

若系统包括m个并联子系统，其中由ni个单元并联组成第i个子系统，设第i个子系统中第j个单元的可靠度为Rij,i=1,2,…,m,j=1,2,…,ni，则由独立失效的子系统或零部件单元构成的串-并联系统的可靠度为

(3)

1.4 并-串联系统可靠性模型

并-串联系统是由串联子系统或零部件单元构成的并联结构，其可靠性模型框图如图4所示.在计算系统的可靠度时，可先计算每一个串联子系统或零部件构成的等效单元，然后并联成整个系统.

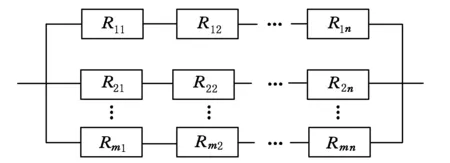
图4 并-串联系统可靠性框图模型

若系统包括m个并联子系统，其中由ni个单元串联组成第i个子系统，设第i个子系统中第j个单元的可靠度为Rij,i=1,2,…,m,j=1,2,…,ni，则由独立失效的子系统或零部件单元构成的并-串联系统的可靠度为

(4)

串联系统和并联系统是最简单的系统可靠性模型，是分析复杂系统的基础，串-并联系统和并-串联系统较为复杂，称为混联系统.

2 基于动态规划法的可靠性冗余优化方法

2.1 系统可靠性冗余优化的数学模型

对系统进行可靠性冗余优化的数学模型[3-5]主要包括：

1) 在满足系统资源为可靠度函数的约束条件下，各级子系统为最优冗余时使系统可靠度达到最大，即

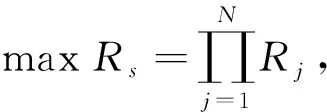
(5)

式中：Rs为作动器系统的可靠度；Rj为第j零部件或子系统的可靠度；gij(Rj)为消耗于第j零部件或子系统上的资源，它与子系统或零部件可靠度Rj的关系既可以是线性关系，也可以是非线性关系；bi为第i个资源的最大或最小总数.

2) 在每级消耗的资源为冗余数的函数约束条件下，使系统的可靠度达到最大，即

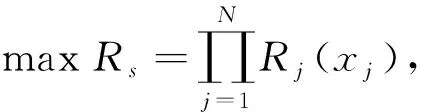
(6)

式中：Rj(xj)为系统第j级(第j个子系统或零部件)的可靠度，是零部件或子系统的冗余数.

3) 在各级子系统可靠度是冗余数的函数时，并满足系统总可靠度的约束条件下，使系统消耗的资源最少，即

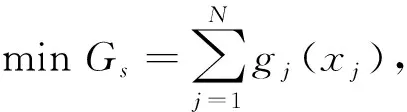
(7)

式中：Gs为系统的总资源，可以是系统消耗的费用，也可以是系统消耗的体积或质量.

4) 对于复杂系统的冗余可靠度，可用条件概率或者网络算法[6]得到，其优化模型为

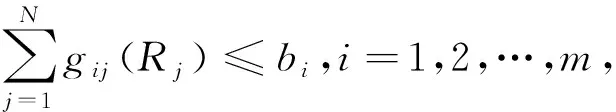
(8)

在此，系统的可靠度是零部件或子系统的可靠度Rj的函数.

2.2 动态规划法用于冗余可靠性优化的几种方法

动态规划法是可靠性设计及优化方法之一，故而主要介绍3种基于动态规划法的冗余可靠性优化方法.

1) 基本动态规划法原理 由文献[7-10]可得基于动态规划法的可靠度优化方程为

(9)

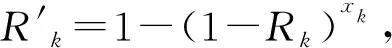
由式(9)所示的约束条件可得系统的状态转移方程为

(10)

故基于动态规划法的可靠度优化模型为

(11)

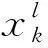
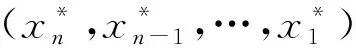
2) 基于拉格朗日乘子的动态规划法 当作动器系统可靠性优化目标函数的约束条件较多时，可用拉格朗日乘子方法来降低模型的维数.若系统约束条件为

引入拉格朗日乘子λ作为一个惩罚项，则系统的可靠性冗余优化模型变为

(12)

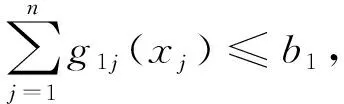
于是，对系统进行动态规划优化的基本方程变为

(13)

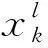
3) 基于控制序列的动态规划法[11]基于控制序列对系统进行动态规划的可靠性冗余优化的模型为

(14)

在求解多约束系统的可靠度冗余优化时，因其计算工作量大，故可通过系统结构的控制条件进行简化.

若系统所满足的约束条件为

且有：Rs(x′)≥Rs(x).

综上可知，由系统的结构x′去控制另一个系统的结构x，即：若系统的控制结构可靠性好，且资源消耗也少，满足式(14)的所有资源约束条件，也不受其它冗余数分配序列s的控制，称其为一个控制序列.

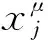
3 滚珠螺旋作动器的可靠性冗余优化

3.1 滚珠螺旋作动器电液控制系统

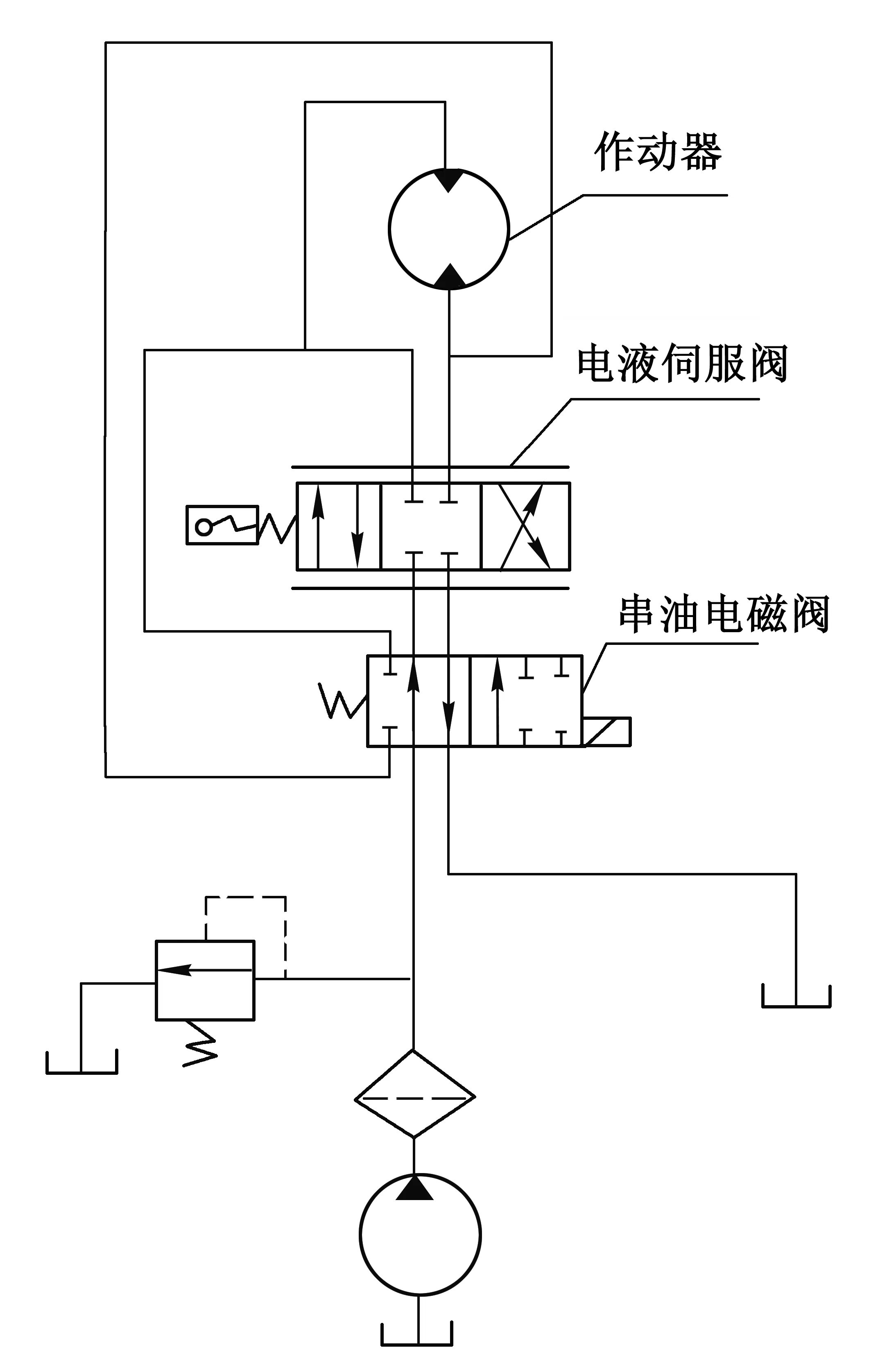
图5 滚珠螺旋作动器系统

图5所示为滚珠螺旋作动器电液控制系统，主要由电液控制组件、液压系统管阀组件以及滚珠螺旋作动器等组成[12].电控组件包括伺服控制器及放大器、电磁阀控制器、电机控制驱动器等；管阀组件包括电液伺服阀、电磁阀、溢流阀、液压管路等组件；滚珠螺旋作动器包括滚珠螺旋副、滚珠花键副以及液压油缸组件等.滚珠螺旋作动器是将直线运动转换为旋转摆动的液压-机械复合传动机构，其结构原理[13-14]如图6所示.此外，滚珠螺旋作动器还可作为液压系统的液压摆动马达来使用，其特点是效率高、驱动力矩大，广泛应用于工程机械液压系统领域.

3.2 滚珠螺旋作动器系统组成及可靠性要求

由图5及系统特点可知，3个组件中任何一个出现故障整个系统就不能工作，引起系统失效.系统的可靠性模型框图，如图7所示.该系统为3级串联，在进行系统可靠性分配时，为提高整个系统工作的可靠性，对每一组(子系统)的部件都进行零部件的冗余配置设计，并使其能自动投入系统的工作中.很显然，零部件的冗余数越多，则系统可靠性就越高，但整个系统的费用、质量及体积等资源均相应增加，系统的机动性和工作精度也将降低.在以上条件限制下要使整个系统的可靠性达到最大，则必需合理选择各子系统零部件的冗余件数.

对于滚珠螺旋作动器系统，只要满足对系统提出的资源(质量)约束条件要求，每一级子系统都可以进行零部件的冗余配置设计，但应基于组合方案的不同，选取最大可靠性值.滚珠螺旋作动器系统各组成子系统或零部件可靠性及资源“质量”见表1，其约束条件是要求整个作动器系统的资源(质量)不超过40 kg，配置其零部件的冗余数使系统可靠性为最大.

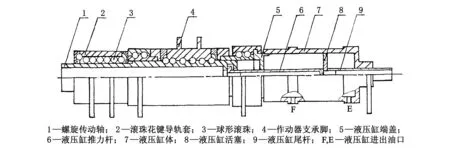
图6 滚珠螺旋作动器结构原理图

图7 作动器系统的可靠性框图

表1 滚珠螺旋作动器系统基本数据

3.3 滚珠螺旋作动器系统冗余可靠性优化计算

由式(14)可得作动器系统的可靠性优化模型

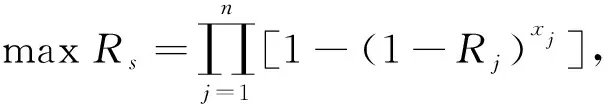
求解最优滚珠螺旋作动器系统结构及可靠性，按基于控制序列的动态规划法对系统进行可靠性优化分析计算.

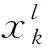
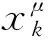
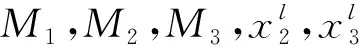
3.3.2 各级子系统冗余资源及可靠度计算

x1=1时，M1=6 kg,R1=0.9,

x1=2时，M1=12 kg,R1=1-1-0.92=0.99,

x1=3时，M1=18 kg,R1=1-1-0.93=0.999,

x1=4时，M1=24 kg,R1=1-1-0.94=0.999 9.

x2=1时，M2=10 kg,R2=0.8,

x2=2时，M2=20 kg,R2=1-1-0.82=0.96,

x2=3时，M2=30 kg,R2=1-1-0.83=0.992,

x3=1时，M3=8 kg,R3=0.9,

x3=2时，M3=16 kg,R3=1-1-0.92=0.99,

x3=3时，M3=30 kg,R3=1-1-0.93=0.999.

3.3.3 系统各级不同冗余度可靠度及其约束资源计算

1) 第1级与第2级不同冗余度组合的可靠度及其约束资源计算 由第1级和第2级组合成系统的控制序列，由其消去别的控制元素而得到.其计算过程如下：

当x1=1、x2=1时的可靠度

R12=R1×R2=0.9×0.8=0.72，

约束资源

M12=M1+M2=6+10=16 kg，

当x1=2、x2=1时的可靠度

R12=R1×R2=0.99×0.8=0.792，

约束资源

M12=M1+M2=12+10=22 kg，

以此类推，得到的所有计算结果见表2.

2) 第1级、第2级与第3级不同冗余度组合的可靠度及其约束资源计算 由表2可知，元素(x1,x2)= {(4,2)、(2,3)、(3,3)、(4,3)}已经超过可用资源的质量约束，因此，不与第3级组合计算.将表2中剩下的元素与第3级不同冗余度组合，计算系统的可靠度及资源.

当x3=1、(x1,x2)= (1,1)时的可靠度

R123=R12×R3=0.72×0.9=0.648，

约束资源

M123=M12+M3=16+8=24 kg，

当x3=2、(x1,x2)= (1,1)时的可靠度

R123=R12×R2=0.72×0.99=0.712 8，

约束资源

M123=M13+M2=16+16=32 kg，

以此类推，所有计算结果见表3.

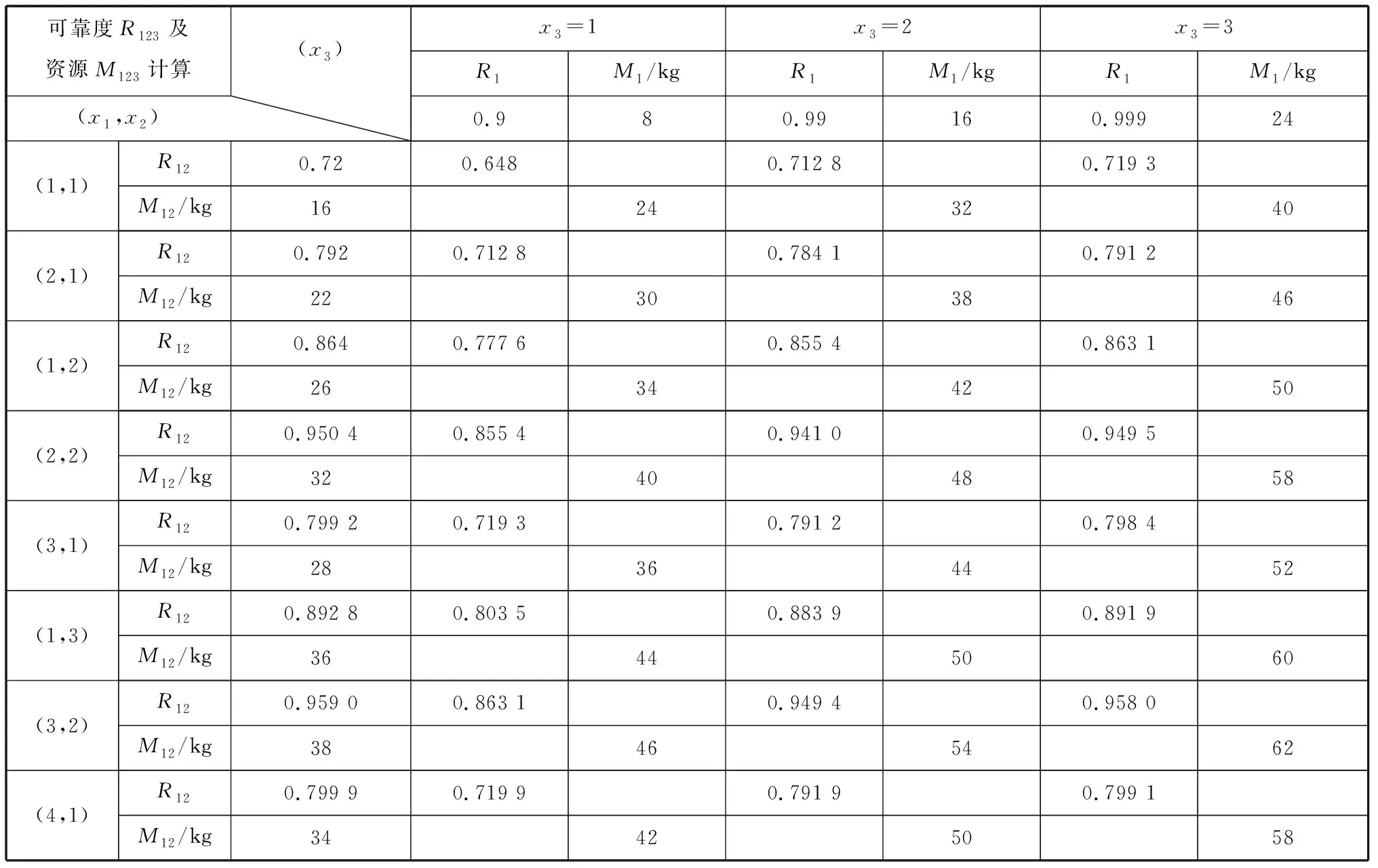
表3 第1级、第2级及第3级冗余度组合(x1,x2，x3)的可靠度及资源计算

表3中满足资源质量约束条件的元素就是基于控制序列的动态规划法对系统进行的冗余度可靠性优化设计的结果.由表3可得最优控制序列为

(x1,x2,x3)={ (1,1,1)、(1,1,2)、(1,1,3)、(2,1,1)、(2,1,2)、(2,2,1)、(3,1,1)}.

由表3可查得最优控制序列各元素的可靠度及资源(质量)值.其中，系统冗余度组合(2,2,1)的可靠度为最大.即基于控制序列的动态规划法求解系统冗余可靠度的最优解为

即：当系统的第1级电控组件冗余数为2，第2级的阀管组件为2，第3级的作动器为1时，系统的可靠度为最大.

4 结语

本文介绍了系统可靠性串联系统、并联系统、串-并联系统、并-串联系统的各方框图基本模型；分别建立了基于动态规划法对系统冗余可靠度优化的数学模型及及其优化方法；基于控制序列的动态规划法对滚珠螺旋作动器系统进行了冗余可靠度优化的设计计算，在系统电控元件、管阀元件以及作动器组合时满足约束条件下，得到了可靠度为最大的各级部件冗余度.