齿轮啮合过程弯曲强度有限元分析*

涂文兵，杨锦雯，罗 丫，任继文

(华东交通大学 机电与车辆工程学院，江西 南昌 330013)

0 引言

轮齿折断是机械传动设备中最常见的齿轮损伤形式，也是造成齿轮失效的主要原因。轮齿受力后，在齿根部产生的弯曲应力最大，且在齿根过渡圆角处有应力集中。齿根的弯曲应力随啮合点位置的变化而不同，如果齿根的应力超过了材料的极限应力则会造成轮齿过载折断。因此，分析齿轮不同啮合位置时齿根的弯曲应力具有重要的理论价值和工程意义。

齿轮的静强度研究自齿轮应用以来就受到了国内外学者的重视。Conry[1]通过编程计算得到了齿轮的弹性变形和接触应力分布；Refaat[2]将变分不等式与有限元接触分析相结合，计算了齿面接触应力和齿根应力；陶振荣[3]提出了一种将齿轮接触疲劳强度的常规设计与可靠性设计相结合的改进计算方法，为齿轮的小型化设计提供参考；徐跃进[4]计算分析了锥齿轮啮合过程中的接触应力，并与赫兹公式计算结果比较，证明了有限元仿真法的精确有效性；董淑婧[5]通过两种加载方案对主、从动齿轮的有限元模型进行分析计算，得到了主、从动轮的弯曲应力；王小群等[6]采用三维接触有限元技术研究了不同齿根过渡曲线对齿轮齿根弯曲疲劳强度的影响，为选择不同齿轮加工方法提供了理论依据；郭辉等[7]用三维接触有限元法计算了面齿轮副啮合过程中及其参数变化时弯曲应力的变化；陈玲等[8]建立了齿轮二维和三维有限元模型，分别研究了在静载荷和冲击载荷作用下齿轮能承受的最大载荷值；赵韩等[9]较系统地介绍了近年来齿轮技术新的发展和应用现状，并提出了一些需要解决的问题。综上，目前关于齿轮静强度的研究主要集中在对齿轮接触应力的分析方面，较少涉及到齿根弯曲应力，特别是对齿轮不同啮合位置时齿根的弯曲应力分析。因此，本文对齿轮啮合过程的弯曲强度进行有限元分析。

1 齿轮啮合过程弯曲强度有限元分析流程

本文利用有限元分析软件ANSYS建立一对渐开线直齿圆柱齿轮的接触有限元模型，并对其进行非线性静力学分析。通过与理论计算结果的比较，验证本文所用分析方法的准确可靠性，并在此基础上进一步分析齿轮不同啮合位置下齿根的弯曲强度。通过设置不同加载位置来仿真啮合位置的真实变化，然后求解计算出不同啮合位置下齿根的弯曲应力，从而得到齿轮弯曲强度随啮合位置的变化规律。齿轮啮合过程弯曲强度有限元分析流程如图1所示。

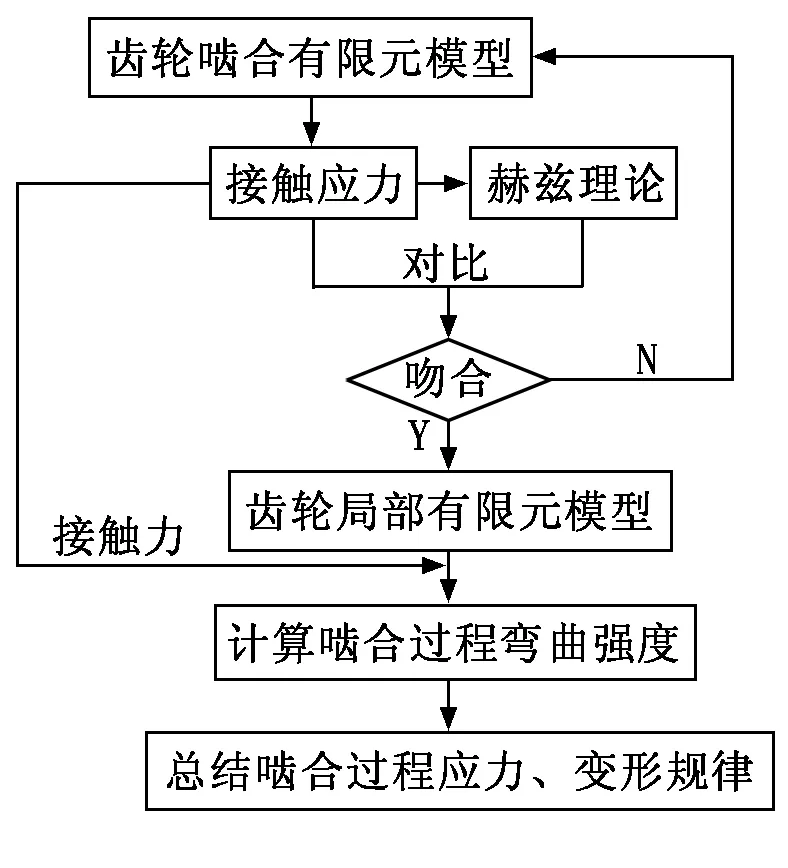
图1 齿轮啮合过程弯曲强度有限元分析流程

2 有限元模型建立

本文以渐开线直齿圆柱齿轮为研究对象，其结构参数见表1。

齿轮传动是依靠轮齿依次啮合而实现的，正确啮合的两渐开线直齿圆柱齿轮的法向齿距Pn必须相等。齿轮的啮合从主动轮的齿根推动从动轮的齿顶开始，到主动轮的齿顶推动从动轮的齿根结束，轮齿依次啮合，形成连续传动，齿轮啮合过程的齿廓图如图2所示。图2中，N1N2为公法线，B1B2为实际啮合线，Pn为法向齿距，ra1为主动轮齿顶圆半径，rb1为主动轮齿根圆半径，ra2为从动轮齿顶圆半径，rb2为从动轮齿根圆半径。重合度计算公式为：

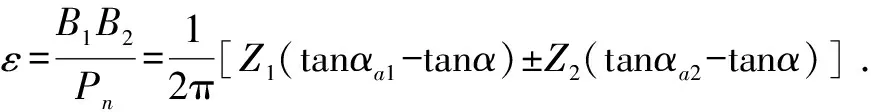
(1)

其中：Z1为主动轮齿数;Z2为从动轮齿数;αa1为主动轮齿顶圆压力角;αa2为从动轮齿顶圆压力角;α为啮合角。已知Z1=24，Z2=48，αa1=29.841°，αa2=25.564°，α=20°。将相关参数代入公式(1)中求得齿轮重合度为1.67，表明齿轮啮合过程中，单齿对工作与双齿对工作交替进行，且转过一个基圆齿距期间有67%的时间是双齿啮合，27%的时间是单齿啮合。由于单齿啮合时齿轮所受应力最为恶劣，因此本文主要对单齿啮合过程中齿轮的弯曲强度进行分析。

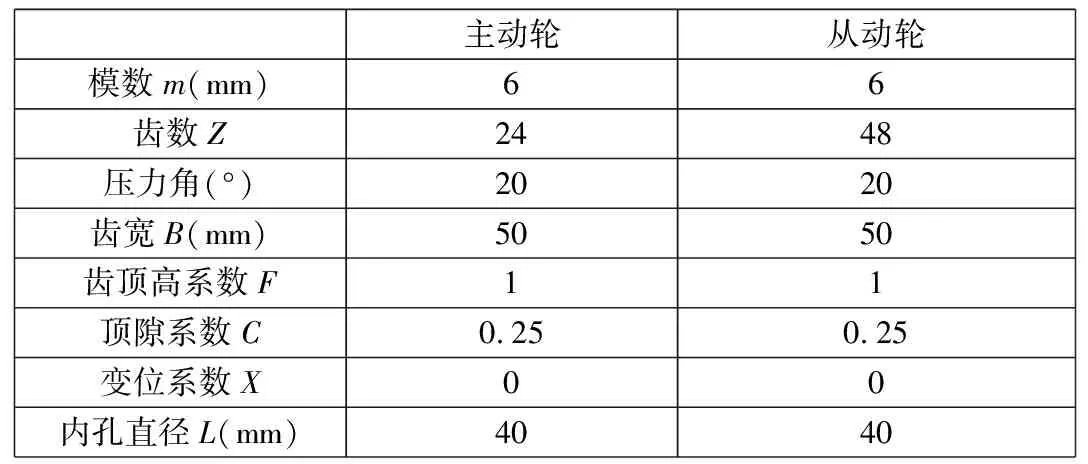
表1 渐开线直齿圆柱齿轮基本参数

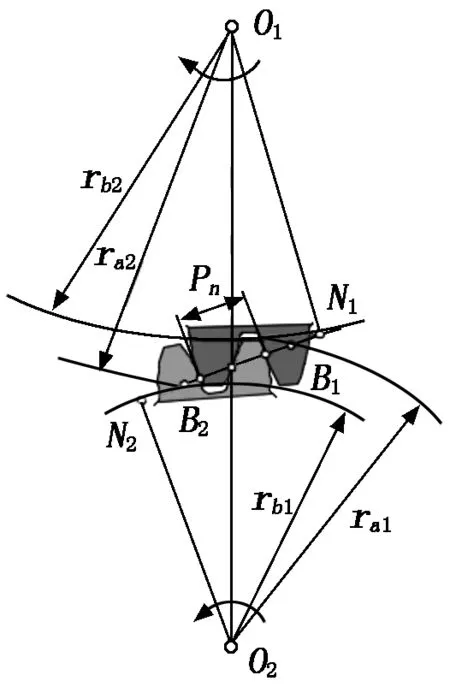
图2 齿轮啮合过程的齿廓图

利用大型建模软件Pro/E创建齿轮啮合的实体模型，保存为igs格式后导入ANSYS中。齿轮材料为40Cr，选用各向同性材料进行模拟，设置密度为7 850 kg/m3、弹性模量为2.06×105MPa、泊松比为0.3。选用Solid-brick 8 node 185单元对模型进行网格划分，为保证计算精度同时节约计算时间，对轮齿啮合部位进行网格细化，设置全局网格大小为6 mm，齿轮啮合部位为0.8 mm，最终得到103 632个单元、456 892个节点。齿轮接触采用点-面、柔性-刚性接触，设置摩擦因数为0.3。主动轮传递的扭矩为487 N·m，齿轮内孔上的节点总数为1 404个，根据齿轮运动规律，对从动轮中心孔上所有节点进行全约束，在主动轮中心孔面节点上施加切向力以模拟扭矩。齿轮啮合有限元模型如图3(a)所示。在ANSYS中创建齿轮局部实体模型，设置材料属性同上。选用Plane183单元对模型进行网格划分，最终得到5 915个单元、18 234个节点。对齿轮内孔和两侧面进行全约束，得到的齿轮局部有限元模型如图3(b)所示。

图3 齿轮有限元模型

3 结果与分析

3.1 齿轮接触应力分析

用完全牛顿-拉普森迭代算法对齿轮接触模型进行静力学求解，得到的齿轮接触等效应力云图如图4所示。从图4中可以看出：应力主要集中在轮齿接触处和齿根处，并向四周逐渐衰减，齿轮传动中齿面受到的最大接触应力为605 MPa。按齿轮接触强度的传统计算方法，接触应力计算公式为：

(2)

其中：K为载荷系数;T1为主动轮传递的扭矩;Φd为齿宽系数;d1为主动轮分度圆直径;u为传动比;ZH为区域系数;ZE为弹性影响系数;Zε为重合度系数。已知K=1.81，T1=487 N·m，Φd=0.347，d1=0.144 m，u=2，ZH=2.5，ZE=189.8,Zε=0.881。将已知参数代入公式(2)中，求得接触应力的理论值为668 MPa，进而算出相对误差η=9%，由此验证了本文所用的分析方法的有效性，为下文的啮合过程齿根弯曲强度分析提供了可靠性保障。

3.2 齿轮啮合过程弯曲应力分析

在齿轮的运动过程中，轮齿的受力点会随着啮合线位置的变化而变化，本文仅对应力最为恶劣的单齿啮合过程进行分析。在从动轮一侧接触面上设置6个加载位置(如图5所示)，1为单齿啮合起始点，6为单齿啮合终止点。以加载位置的移动来仿真啮合位置的真实变化，从上文接触模型的计算结果中提取出接触力，用静力等效的原则将载荷均匀地加在接触表面[10]，求解得到单齿啮合过程中不同啮合位置下齿轮的弯曲应力，如图6所示。

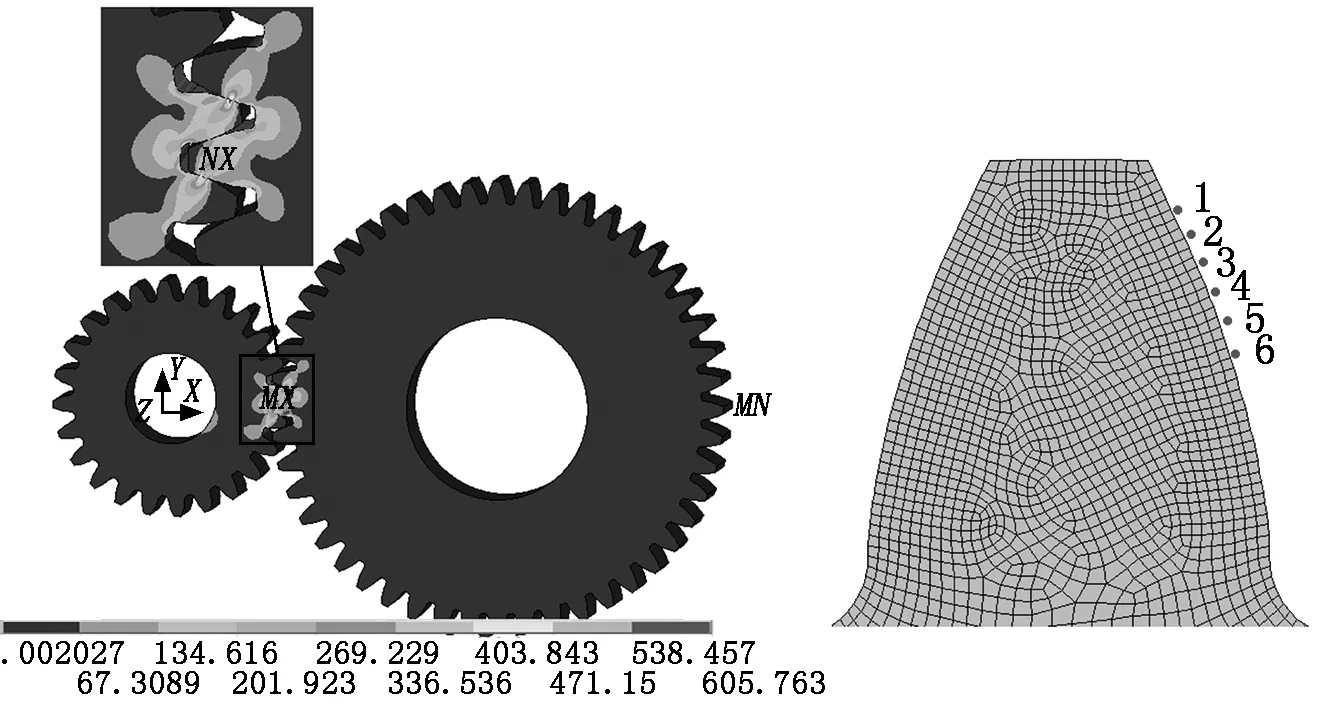
图4齿轮接触等效应力云图图5加载位置示意图

由图6可以看出：在单齿啮合过程中，受载齿的齿根过渡圆角处出现明显的应力集中现象，该齿上的应力水平较高，邻齿和齿轮中心几乎无应力；当载荷施加在单齿啮合最高点时，齿根应力最大；随着啮合位置的降低，应力分布区域扩展，齿根应力减小；当载荷施加在单齿啮合最低点时，最大应力位置由齿根处移至加载位置处，齿根应力集中现象得到缓解。

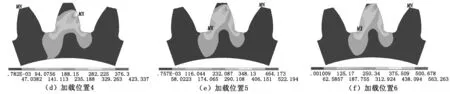
图6 单齿啮合过程不同加载位置弯曲应力云图

为了定量分析齿轮强度与啮合位置的关系，提取加载侧齿根最大应力绝对值、非加载侧齿根最大应力绝对值以及齿轮最大变形量进行数据分析，结果如图7和图8所示。

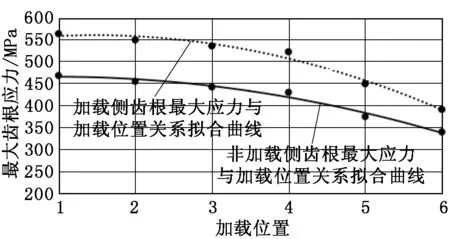
图7 加载位置与齿根最大应力的关系

图8 齿轮最大变形量与加载位置的关系

在单齿啮合过程中，齿轮加载侧受力拉伸，非加载侧受力压缩。由图7可知：受拉侧应力的绝对值始终略大于受压侧应力的绝对值，且材料的抗压强度远大于抗拉强度，因此齿轮啮合过程中最危险的位置为加载侧齿根圆角处。通过对数值点进行曲线拟合可知，两侧最大应力在单齿啮合过程中均呈二次抛物线衰减。

由图8可知：在单齿啮合过程中，齿轮的最大变形发生在啮合的最高点，且位于齿顶圆附近。通过对数值点进行曲线拟合可知，齿轮最大变形量在单齿啮合过程中呈二次抛物线衰减。

4 结论

本文基于ANSYS对齿轮啮合过程弯曲强度进行分析，得出如下结论：

(1) 齿轮啮合过程中最危险的位置为加载侧齿根圆角处，持续的应力集中容易造成轮齿的折断，因此在齿轮的设计过程中应注意提高齿根圆角处的强度。

(2) 齿轮单齿啮合过程中，两侧齿根弯曲应力和最大变形量均呈二次抛物线衰减。

(3) 鉴于ANSYS分析的快捷、直观和准确性，在齿轮设计过程中可以使用有限元分析来代替传统方法进行强度校核，以缩短研发周期，提高设计效率。