空气弹簧失效对地铁车辆动力学性能的影响

李朝曦，傅茂海，邹纪操，胡静涛

(西南交通大学 机械工程学院，四川 成都 610031)

0 引言

现有文献多是研究空气弹簧自身性能或其正常状态时对车辆性能的影响，而针对空气弹簧失效时对车辆的动力学性能影响研究较少。本文基于多体动力学理论，以某地铁列车为研究对象，在SIMPACK软件平台上建立整车的动力学性能仿真模型，分别计算了空气弹簧在正常情况和失效情况下的动力学性能，进一步对比动力学性能指标，探究空气弹簧失效对地铁车辆转向架动力学性能的影响。

1 动力学仿真计算模型

本文研究的地铁车辆最高运营速度为80 km/h，最高试验速度为88 km/h，适用于轨距为1 676 mm的宽轨轨道。转向架主要由H型整体式焊接构架、一系悬挂装置、二系悬挂装置、驱动及牵引装置以及基础制动装置等部件组成。其中一系悬挂装置采用圆锥橡胶弹簧，二系悬挂装置采用空气弹簧，并配有垂向及横向油压减振器、横向弹性止挡、抗侧滚扭杆装置等。在动力学性能计算模型中将轮对、轴箱、转向架构架、车体视为刚体，根据真实情况输入了弹性止挡的特性曲线，设定减振器和牵引拉杆的橡胶关节刚度值，并且考虑了轮轨非线性接触几何关系、轮轨非线性蠕滑以及悬挂系统的非线性，进而保证了仿真过程的真实、可靠性。在多体动力学软件SIMPACK环境中建立的地铁车辆系统动力学计算模型如图1所示，车体及转向架主要参数如表1所示。

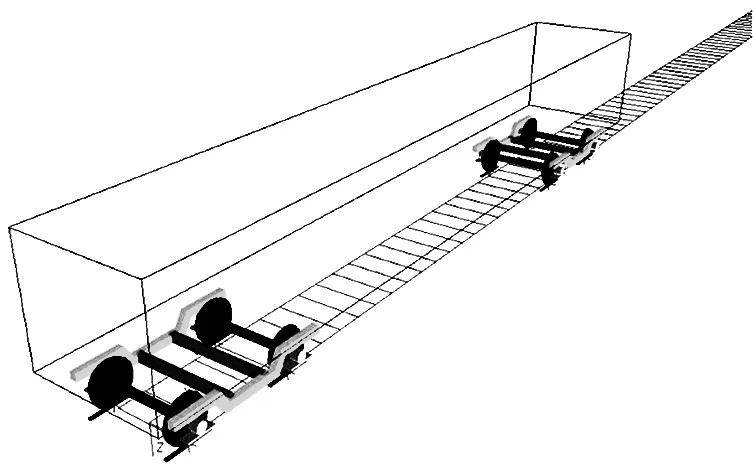
图1 地铁车辆动力学计算模型

2 空气弹簧正常情况下动力学性能分析

本文考虑了空车、重车两种工况，分别计算地铁车辆的直线运行平稳性以及曲线通过性能，并根据相关标准进行评估。

表1 车体及转向架主要参数

2.1 直线运行平稳性计算结果

在进行直线运行平稳性分析中，将同时考虑车辆在横向和垂向两个方向的运动，因此，车辆运行过程的数学模型可描述为:

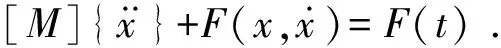
(1)

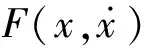
激扰力是由于轨道不平顺引起的，通过输入时域内的轨道不平顺参数，用逐步积分法求解非线性系统的响应性，计算中的轨道不平顺参数采用美国Ⅴ级线路谱输入，利用四阶龙格—库塔数值积分法求解式(1)，得到车辆的位移、速度和加速度响应。根据车体的振动加速度随时间的变化过程，利用快速傅立叶变换(FFT)求出不同频率下的横向和垂向振动加速度Ay、Az，并且根据Sperling平稳性指标法求出车体的横向及垂向平稳性指标Wzy、Wzz。根据设计要求，该转向架的动力学性能应符合GB/T 5599—1985、UIC518等标准和技术条件要求。GB/T 5599—1985规定：客车运行平稳性采用车体上心盘(转向架中心)偏离横向1 000 mm处地板面上的最大横向及垂向加速度、横向及垂向平稳性指标来表示。UIC518规定：客车最大横向和垂向加速度均不能超过2.5 m/s2，平稳性指标应满足表2中的良好级，即横向和垂向平稳性指标均应小于2.75。

表2 GB/T 5599—1985规定的客车平稳性等级

通过计算，该地铁车辆在88 km/h速度范围内的横向及垂向振动加速度Ay、Az和横向及垂向平稳性指标Wzy、Wzz如图2、图3所示。

由图2、图3可以看出：在88 km/h的速度范围内，随着运行速度的提高，车辆的振动加速度和平稳性指标基本上呈上升的趋势，且空车的平稳性较重车差；该地铁车辆的横向及垂向最大加速度均小于2.5 m/s2，小于UIC518规定的限度值，其横向及垂向平稳性指标均小于2.5，达到GB/T 5599—1985规定的优级标准。

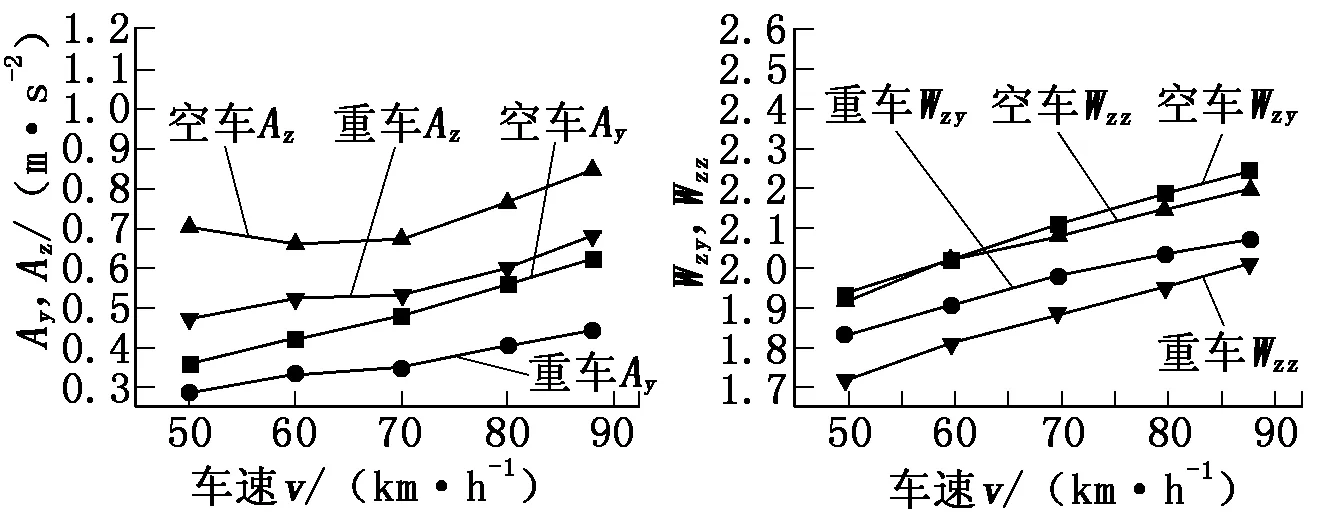
图2空气弹簧正常情况下横向及垂向加速度图3空气弹簧正常情况下横向及垂向平稳性指标

2.2 曲线通过性能计算结果

线路曲线是由一段超高和曲率不断变化的缓和曲线以及一段超高和曲率都固定的圆曲线组成的，车辆通过曲线时的非线性运动微分方程可表示为:

(2)

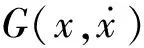
利用四阶龙格—库塔积分法求解式(2)，从车辆第一轮对进入曲线起点时开始积分。由于轮轨间的垂向力与轮轨间的蠕滑力相互影响，因此在积分收敛前需要反复迭代以保持计算精度。根据线路条件及技术要求，线路设置如表3所示。在计算中输出车辆通过曲线时的轮轴横向力Hmax、脱轨系数及轮重减载率的最大值，计算结果应当符合GB/T 5599—1985所规定的限值，其中轮轴横向力Hmax、脱轨系数、轮重减载率的具体限值如表4所示。曲线通过性能计算结果如图4所示。

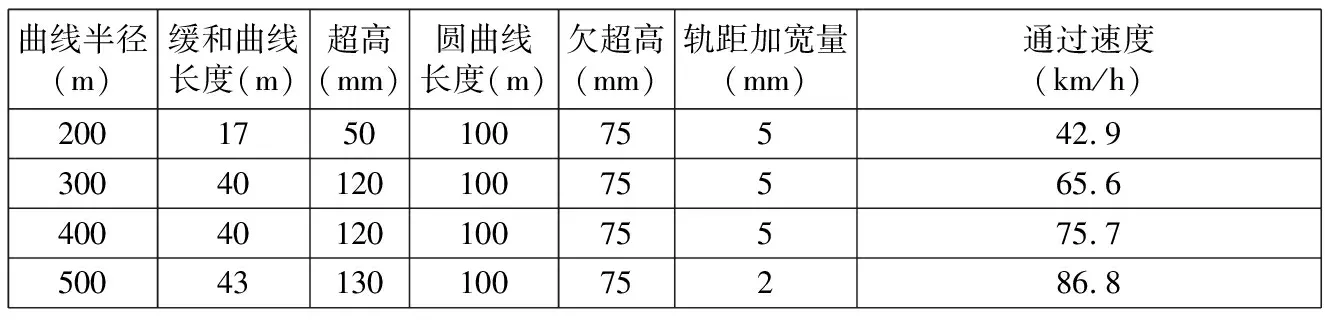
表3 线路条件设置

表4 GB/T 5599—1985规定的曲线通过性能指标限值

从图4可以看出：该车辆以75 mm的欠超高通过半径为200 m、300 m、400 m和500 m的圆曲线时，其在空、重车工况下的轮轴横向力、脱轨系数和轮重减载率均小于GB/T 5599—1985所规定的限度值，其曲线通过安全性能满足要求。

3 空气弹簧失效对动力学性能的影响

通常空气弹簧本体由上盖板、橡胶囊、下盖板以及应急弹簧组成，车体或者摇枕的空气弹簧座与上盖板相连，应急弹簧与构架的空气弹簧座相连。此外，在上盖板和应急弹簧接触面上设有磨耗板，当空气弹簧失效后，上盖板磨耗板与应急弹簧磨耗板接触后，纵向和横向会粘着或相对滑动[9]。本文研究的转向架所使用的应急弹簧为锥形橡胶弹簧，在垂向受到压、剪复合力的影响，由试验得到的应急弹簧在空、重车条件下的垂向以及径向刚度如表5所示。因此在对空气弹簧失效情况进行仿真时，考虑了空气弹簧刚度的变化量、空气弹簧失效所造成的车体下沉量以及车体与应急弹簧之间的摩擦作用，其中摩擦因数为0.08。

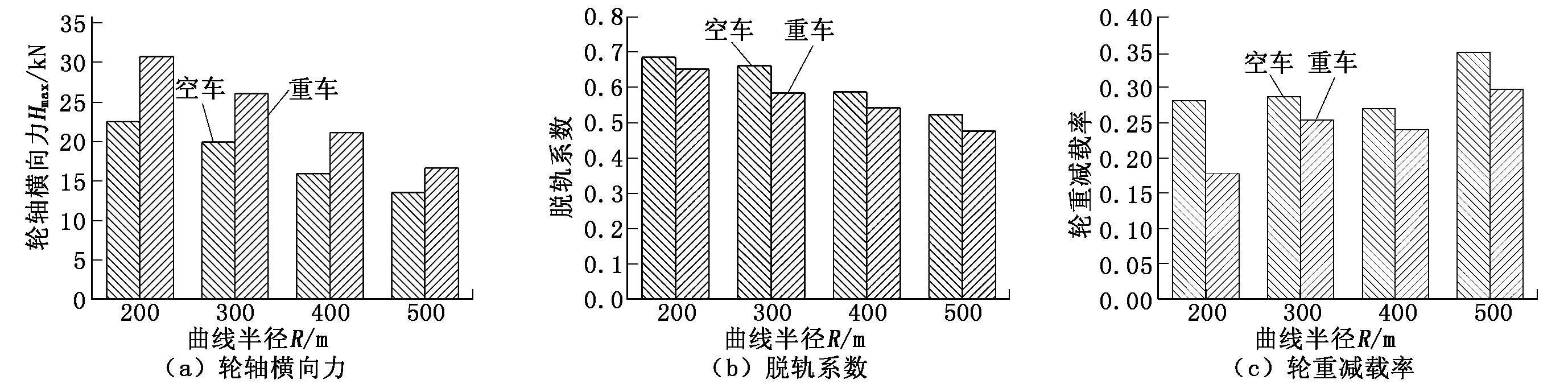
图4 空气弹簧正常情况下车辆的曲线通过性能指标

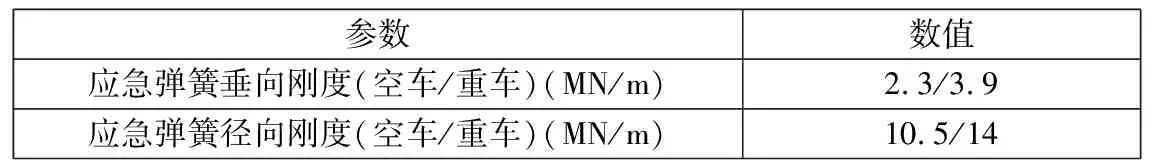
参数数值应急弹簧垂向刚度(空车/重车)(MN/m)2.3/3.9应急弹簧径向刚度(空车/重车)(MN/m)10.5/14

3.1 对直线运行平稳性的影响

对空气弹簧失效时车辆的直线运行平稳性进行计算，其线路、速度以及轨道激励设置与正常工况下相一致，分别计算后位转向架空气弹簧失效和空气弹簧全部失效时的横向及垂向振动加速度Ay、Az和横向及垂向平稳性指标Wzy、Wzz。计算结果如图5～图8所示。

图5后位转向架空气弹簧失效时的振动加速度图6后位转向架空气弹簧失效时的平稳性指标图7空气弹簧全部失效时的振动加速度图8空气弹簧全部失效时的平稳性指标

由图5～图8可以看出：当转向架空气弹簧失效时，车辆的运行平稳性变差，而且空气弹簧全部失效相较于仅后位转向架空气弹簧失效的情况对车辆的平稳性影响更为明显;当后位转向架空气弹簧失效时，在88 km/h的速度范围内，车体的振动加速度均在限定值2.5 m/s2以下;横向平稳性指标在速度超过80 km/h时无法满足GB/T 5599—1985规定的优级标准，但都能达到良好标准，而垂向平稳性指标在超过65 km/h时无法达到优级标准，并在速度超过80 km/h时空车工况不能满足良好标准，但是在合格标准的范围内;当空气弹簧全部失效时，横向振动加速度均在限定值2.5 m/s2以下，而垂向加速度在运行速度达到78 km/h左右时超过UIC标准规定的2.5 m/s2;横向平稳性指标在运行速度不超过65 km/h时能够满足GB/T 5599—1985的优级标准，当速度约为85 km/h时，横向平稳性指标不能满足GB/T 5599—1985的良好标准，但是在合格标准的范围内;当运行速度低于63 km/h时，垂向平稳性指标满足GB/T 5599—1985的优级标准，而当速度超过77 km/h时，该指标不能满足GB/T 5599—1985的良好标准，但是在合格范围以内。

3.2 对曲线通过性能的影响

当后位转向架空气弹簧失效和空气弹簧全部失效时，空车和重车工况下车辆通过不同曲线时的轮轴横向力、脱轨系数和轮重减载率如图9所示。

由图9可以看出：当空气弹簧失效时，车辆通过曲线时的各项动力学性能指标的值大幅度提高，曲线通过能力变差；通过对比分析，相较于部分空气弹簧失效时的动力学性能指标，当空气弹簧全部失效时通过曲线更加危险；而在部分曲线线路上，车辆的轮轴横向力、脱轨系数、轮重减载率超过了GB/T 5599—1985规定的安全限值，需要限速通过曲线。

4 结束语

本文基于多体动力学理论，研究了空气弹簧失效对地铁车辆转向架动力学性能的影响，得出如下结论。

(1) 在空气弹簧正常的情况下，该地铁车辆在直线线路上的平稳性较好，振动加速度低于UIC518标准规定的2.5 m/s2的限度值，且平稳性指标满足GB/T 5599—1985规定的优级标准；该地铁车辆以75 mm的欠超高通过不同半径的圆曲线时，其不同工况下的轮轴横向力、脱轨系数和轮重减载率均小于GB/T 5599—1985所规定的限度值，曲线通过安全性能满足要求。

(2) 当空气弹簧失效时，该地铁车辆在直线线路上的平稳性变差，且空气弹簧全部失效相较于仅后位转向架空气弹簧失效的情况对车辆的平稳性影响更大。随着运行速度的提高，部分工况下的振动加速度超出了UIC518标准规定的2.5 m/s2的限值，且平稳性指标不能满足优级或者良好标准；当空气弹簧失效时，地铁车辆的曲线通过能力变差，且相较于部分空气弹簧失效时的动力学性能指标，当空气弹簧全部失效时通过曲线更加危险。而在部分线路曲线的部分工况下，车辆的轮轴横向力、脱轨系数、轮重减载率可能会超过GB/T 5599—1985规定的安全指标限值，需要限速通过曲线。

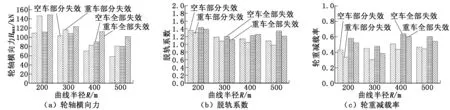
图9 空气弹簧失效时曲线通过性能指标