圆锥形超声变幅杆的设计及实验分析*

王家祥，廖金麒，毛 奇，BAKADIASA KABONGO DJO，轧 刚，2

(1.太原理工大学 机械工程学院，山西 太原 030024；2.精密加工山西省重点实验室，山西 太原 030024)

0 引言

随着科学技术的飞速发展，难加工材料在现代制造业领域的应用越来越广泛，特别是在航空航天、汽车、模具等制造领域，其突出的材料属性，如高强度、耐热性、耐磨性、耐腐蚀性等在提高产品性能方面起了很大的作用。面对材料的高硬度、成型零件的复杂性，特种加工成为加工领域的研究热点，而超声加工就是属于特种加工中的一种[1]。超声加工是利用超声高频振动激励工具冲击有磨料的液体介质，从而产生磨料的冲击、抛磨、液压冲击及由此产生的空化作用来去除材料的加工方法。超声加工的加工对象不受材料的电、化学特性的限制，适合加工各种硬脆材料，如玻璃、陶瓷、石英、人造宝石等，而且工件表面的宏观切削力小，表面无烧伤，无残余应力，一般情况下加工精度较高，且工具易制造，工具和工件相对运动简单[2-4]。

构成超声加工核心的是超声加工系统，超声加工系统主要由超声电源、换能器、变幅杆(包括传振杆)、加工工具以及磨料供给系统等组成。在传统应用中，大多采用一维纵振方式，并按照“全调谐”方式工作。随着超声加工技术研究的发展和不同领域实际应用的特殊需要，超声加工系统的开发和应用都取得了新的进展[5]。

超声变幅杆是超声加工系统的核心组成部分，它的主要作用是把机械振动的质点位移或速度放大，或者将超声能量集中在较小的面积上，即聚能作用。我们知道，超声换能器辐射面的振动幅度在20 kHz范围内只有几微米，而在高声强超声应用中，如超声加工、超声焊接、超声搪锡、超声破化细胞、超声金属成型和某些外科设备及超声疲劳试验等应用中，辐射面的振动幅度一般需要几十微米到几百微米，因此必须在换能器的端面连接超声变幅杆，将机械振动振幅放大。除此之外，超声变幅杆还可以作为机械阻抗变换器，在换能器和声负载之间进行阻抗匹配，使超声能量更有效地从换能器向负载传输[6]。

现阶段，变幅杆的设计方法主要有解析法、机电等效法、有限元法等，应用较多的主要有解析法和有限元法[7-9]。本文基于有限元软件ANSYS对圆锥形超声变幅杆进行设计与实验分析。

1 圆锥形超声变幅杆的理论设计

1.1 质点位移和速度方程

假设变幅杆材料均匀、各向同性，不计机械损耗，平面纵波沿轴向传播。变幅杆示意图如图1所示。变幅杆在一维条件下满足波动方程：

(1)

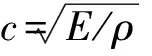
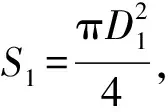
S=S1(1-αx)2.

(2)

(3)

(4)

其中：A1、B1均为求解微分方程产生的系数。

对式(4)求一阶导数后得到质点的速度：

(5)

图1 变幅杆示意图

1.2 频率方程及谐振长度lp

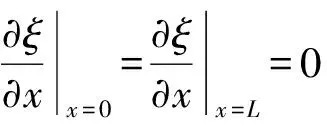
(6)

其中(kL)是公式(6)的根。

(7)

其中：λ为波在介质中传播的波长。变幅杆材料为45钢，波在45钢中的传播速度c=5 162 m/s，λ=c/f，f为振动频率。

1.3 位移节点x0(即振幅为零的点)

(8)

基于式(8)，当x=x0时ξ=0，得位移节点x0满足方程：

(9)

1.4 放大系数Mp

放大系数是指输出端位移幅值与输入端位移幅值之比，由式(8)及边界条件ξ|x=L=-ξ2(ξ2为变幅杆小端输出位移幅值)得放大系数为：

(10)

变幅杆设计频率为20 kHz，超声换能器输出端直径为50 mm，为减少能量传递过程中结合处的能量损耗，取变幅杆输入端直径D1=59 mm、输出端直径D2=16 mm，代入公式(3)可求得N=3.687 5。将N代入公式(6)利用MATLAB软件可求得kL=3.584，再将(kL)代入式(7)和式(10)可得lp=139 mm,Mp=3.01。

2 圆锥形变幅杆的有限元分析

2.1 网格划分

圆锥形变幅杆的设计频率为20 kHz，考虑在高频下连续振动，材料需要具有一定的强度和韧性，并且考虑到加工难易程度及材料成本，选用45钢作为变幅杆材料。45钢材料参数如表1所示。

45钢的许用应力[σ]=300 MPa，利用有限元软件ANSYS建立变幅杆有限元模型，如图2所示。有限元模型的节点数为10 227、单元数为2 083。

2.2 模态分析

选用Block Lanczos方法对两端自由的变幅杆模型进行模态分析，固有频率搜索范围在10 kHz～30 kHz之间，在求解器中选取结果。分析结果显示第4阶为纵振，且固有频率为19 940 Hz，接近20 000 Hz，为我们所需要的结果。变幅杆纵振位移分布云图如图3所示。

表1 45钢材料参数

图2 圆锥形变幅杆的有限元模型

图3 变幅杆纵振位移分布云图

2.3 谐响应分析

选用Full进行谐响应分析，给变幅杆大端施加一个幅值为6 μm的轴向正弦位移，经变幅杆放大后，变幅杆小端输出位移幅值为16.1 μm，故变幅杆放大倍数约为2.68，且位移节点位置在距大端约54 mm处；最大等效应力为49.919 MPa，远小于300 MPa，满足强度要求。变幅杆中心轴上纵振位移曲线及轴向等效应力分布分别如图4和图5所示。

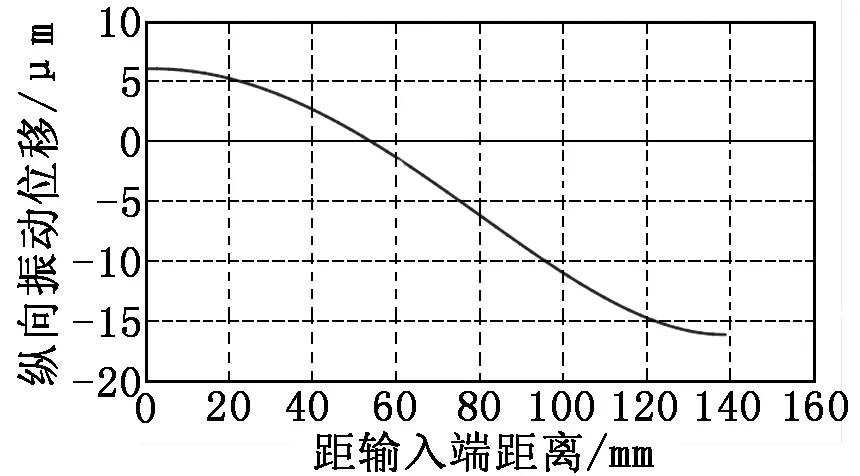
图4 变幅杆中心轴上纵振位移曲线

图5 变幅杆轴向等效应力分布云图

3 阻抗分析

阻抗分析仪能在宽阻抗范围和频率范围内进行精确测量，它在换能器两端加不同频率的低电平电流，通过阻抗计算出换能器或者换能器与变幅杆组成的振动系统的固有频率。

将换能器和变幅杆连接后，使用北京联邦时代电子科技有限公司生产的PV70A阻抗分析仪对超声振动系统进行分析，分析结果如图6所示。实际测得的共振频率为20 512.0 Hz，与仿真得到的频率误差在3%以内。由图6可见导纳圆为单圆且较规整，电导曲线只有一对最大值和最小值，说明变幅杆的设计及与换能器的装配比较成功。

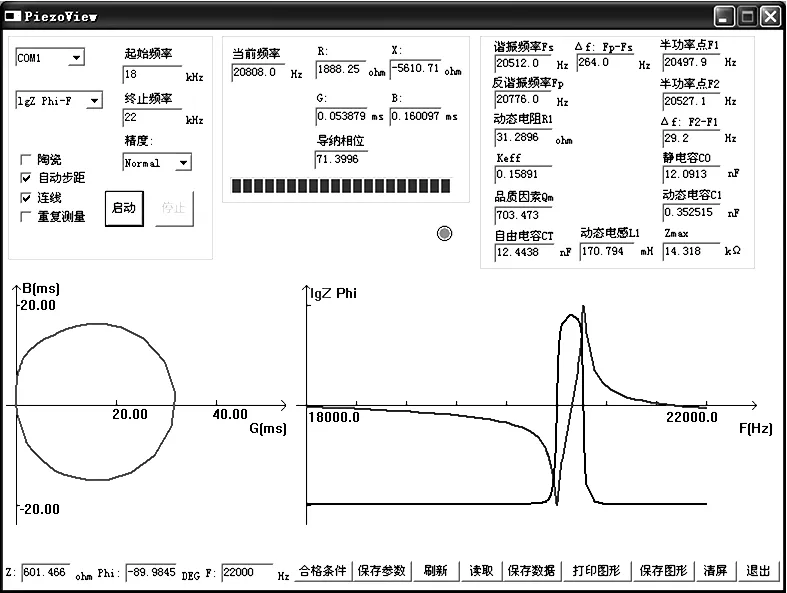
图6 振动系统阻抗分析结果

4 激光测振分析

激光测振仪利用激光多普勒测振技术(LDV)，以非接触方式测量变幅杆输出振幅。用OFV-5000激光测振仪及OFV-505单点式激光头测量振幅，设置位移解码器档位为100 μm/V，将测振仪位移输出信号输入示波器。换能器和振动系统输出振幅的实验测量数据分别如图7和图8所示。

根据实验数据，可算得换能器输出振幅(单峰值)：

振动系统输出端振幅(单峰值)：

5 理论计算、仿真和实验结果对比

变幅杆输入位移振幅为6 μm，三种情况的输出位移振幅分别为：

理论计算：6×3.01=18.06 μm;

仿真：16.1 μm;

实验测量结果：11.9 μm。

分析原因是仿真所用材料参数值与真实值的误差以及实际加工误差，导致实际测量结果与仿真结果有一些误差。

6 结语

基于波动理论设计圆锥形超声变幅杆，用有限元分析软件ANSYS对其进行动力学仿真分析，据此制造出变幅杆并进行阻抗分析和激光测振分析，结果表明制造出的变幅杆机械振动性能较好。说明这种解析法和有限元法相结合的变幅杆设计方法是行之有效的，为更复杂的复合型变幅杆的设计提供了一种思路。

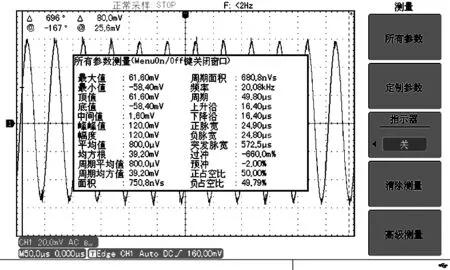
图7 换能器的输出振幅实验测量结果

图8 振动系统输出振幅实验测量结果