政策影响下资源开发与经济增长关系的双重差分检验
2018-12-21王晓轩刘那日苏
王晓轩,刘那日苏
(1.内蒙古科技大学 经济管理学院,内蒙古 包头 014010;2.宁夏大学 经济管理学院,银川 750001)
0 引言
传统经济学认为自然资源是经济增长的必备条件,但是有关的经验研究认为,自然资源禀赋并没有促进经济增长,反而阻碍经济增长,从而形成资源诅咒。资源诅咒现象在我国是否存在?目前存在着争议,徐康宁和王剑以1995—2003年的数据进行分析,认为我国省域层面存在着资源诅咒。邵帅对我国西部省份的检验中,发现西部能源开发与经济增长呈现负相关关系。但是孙大超的研究认为资源丰裕度和区域经济发展没有显著相关性,认为资源诅咒现象在我国省域层面不存在。赵新宇(2012)利用生态足迹模型也发现自然资源与经济发展的诅咒现象在省域层面不存在。资源诅咒现象在我国是否成立是急需进一步检验的问题。
本文以西部大开发政策为例,检验我国省域层面的资源诅咒效应,同时检验西部大开发的政策效果如何,西部大开发政策多大程度协调了资源开发与经济增长的关系。为了判断制度、政策对资源和经济增长之间的关系,本文将采用政策评价计量方法(双重差分方法),对我国政策影响下的资源与经济增长的资源诅咒现象进行检测。
1 检测方法
本文主要是分析西部大开发政策实施、干预带来的因果效应,即处理效应。处理效应根据西部开发省份与非西部开发省份的差异,推断政策实施的效果。处理效应主要的难题是对参与组和未参与组进行分类比较。参与组与未参与组有时候存在着差异,除了参与条件的不同外,其他方面也存在不同。但是,观察接受政策影响的西部省份与未接受政策影响的省份,政府部门公共政策在一个地区实施,在实施过程中,政策实施区域和政策未实施区域会产生差异,因此需要把政策的处理效应从主体的其它差异中分离出来。
1.1 干预组和控制组
在政策影响中,受到政策实施影响的省份,定义为干预组,没有受到政策实施影响的省份是控制组。而西部开发政策自1999年开始实施起,政策实施省份和未实施省份在一定程度上具有政府安排。按照政策实施时间前后和政策实施的不同省份,可以将样本划分为四组,政策实施前的干预省份组(BT)和控制省份组(BC),政策实施后的干预省份组(AT)和控制省份组(AC)。这样就可以比较政策实施的差异和时间序列上的差异,政策实施省份组和未实施省份组的差异有:
在分析研究中,采用干预省份组在政策实施前后的差异来判断样本对象的干预情况,即采用AT-,这种方法会导致不能分离出一些特殊事件和宏观因素影响,得到有偏的干预效果。
还有的方法采用政策实施参与组的因变量值结果值减去控制省份组的因变量结果值,即:-,该方法比较干预省份组和控制省份组结果变量之间的差异,却无法满足政策实施前后的差异。干预组和控制组在政策实施前后可能存在事前差异,如果仅仅比较,干预组试验前后的差异和控制组试验前后的差异,或者试验前干预组和控制组的差异,试验后试验组和控制组的差异,会忽略综合性的政策效应和时间效应。
1.2 双重差分方法简介
能够很好地将时间前后差异和有无参与政策实验两个方面有效结合的方法应该是双重差分方法,双重差分模型既能同时控制除政策干预因素以外的其他因素的影响,又能弥补“自然实验”不能完全随机分配观测样本的问题。同时双重差分构造所需满足的条件较少。
双重差分模型是目前较为领先的政策评价的重要方法,它通过两组(干预组和控制组)数据,按照政策实施前后,开展事前差异,事后差异,以及政策影响的真正效果。双重差分可以剔除一些不可观测的外部因素的干扰,减少伪影响因素,得到政策实施干预的真实影响结果。双重差分方法(DID)利用干预组和控制组、政策实施前后的差,过滤掉了不可观测的不随时间变化的变量,也过滤掉了随时间同等变化的变量。
干预组和控制组的差异构成了横截面上的差异,而政策实施前后的差异构成了时间序列上的差异。利用以上两种差异,双重差分估计可以估计政策实施前后在干预组和控制组之间的差异,反映政策实施的效果。双重差分估计量的具体表达式为:
或者是:
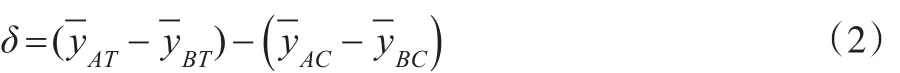
δ就是双重差分估计量,是政策实施对干预组和控制组在被解释变量上的平均处理效应。本文用以上双重差分方法对西部开发政策效应进行评价。双重差分可以有效解决模型内生性问题,规避反向因果偏差、缺失变量偏差等,通过干预组和控制组的差异,准确识别政策带来的净效应。
1.3 政策评价效应的理论分析
双重差分构造了政策实施参与组与政策未参与组,通过设定虚拟变量Tj,t表示政策实施时期的前后,当t=0时,表示政策实施前,t=1表示政策实施后。T1,0表示政策参与的干预组在政策实施前。T0,1表示未参与政策实施的控制组在实施后。
用虚拟变量kj,t表示是否是干预组,当j=0时,表示未参与政策实施的控制组,当 j=1时,表示参与政策实施的干预组;当在政策实施后,参与政策实施,则j=1、t=1。
构造一个基本模型,反映虚拟变量 kj,t、Tj,t对因变量的影响,因变量可以选取与西部开发政策实施有影响的变量(例如国内生产总值增长率)。kj,t表示西部开发政策中,参与政策的省份和未参与政策的省份,按照是否参与西部大开发可以将各省份分为干预组(参与组)和控制组(未参与组)。基本的双重差分影响模型可以表示为:
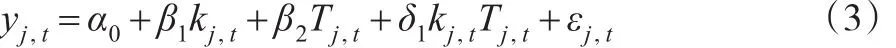
对于控制组,有 k0,t,政策实施前的控制组是 kj,0=0 ,政策实施后的控制组有kj,1=0,则双重差分模型变化为:
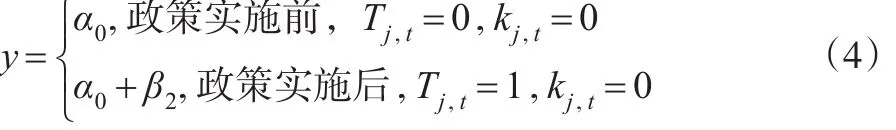
由此,政策实施前后,控制组的省份的因变量(国内生产总值增长率)的平均变动是:

对于干预组,政策实施前的干预组kj,0=1,政策实施后的干预组有kj,1=1,则干预组在西部开发政策实施前后的因变量分别是:
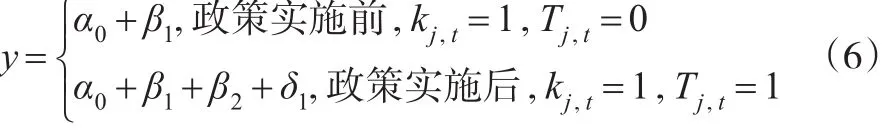
由此,政策实施前后,干预省份组的因变量(国内生产总值增长率)平均变动是:
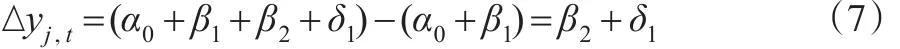
从以上分析看,仅仅比较了因变量的干预组(控制组)在政策实施前后的差异。它们仅反映了时间效应,而西部开发政策效果在干预组和控制组之间的差异并没有体现。为了体现干预组和控制组时间差异和政策实施前后的差异,采用:
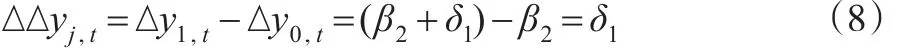
式(8)反映了政策实施前后,干预省份组和控制省份组之间在政策实施的差异,是政策效应差异的体现。
两个虚拟变量kj,tTj,t取值为1或者0,那么双重差分的理论可以表示为表1。

表1 双重差分的时间效应与政策效应
β1表示干预组和控制组的差异,而β2体现时间差异在样本中的影响,δ1综合了干预组、控制组、政策实施期前后的影响,是政策实施对参与西部开发省份与未参与省份的差异,是政策影响的净效果。
在估计模型(3)时,可以采用的方法主要有:独立混合横截面数据模型、综列数据(差分模型和面板模型)。独立混合横截面数据将两个时点的抽样数据进行混合,得到一个数据集,独立混合截面数据每个样本观测点都是独立的观测值,通过两个时点的观测数据混合,加大样本量,获得较精密的估计量和有效果的经验统计量。
混合截面数据由独立抽取的观测值构成,因此满足残差项与解释变量的独立性,E(ej,t|Xj,t)=0 。 独立混合横截面数据可以采用普通最小二乘法(OLS)进行回归,得到无偏的估计量。
2 西部开发政策对省份经济增长影响的双重差分估计结果
2.1 模型介绍
为了判断政府西部大开发政策对各省份经济增长的影响,按照是否参与西部开发政策可以将不同省份分为干预组(参与组)和控制组(未参与组),采用双重差分方法评估西部大开发政策对各省份的影响。基本的双重差分影响模型可以表示为:
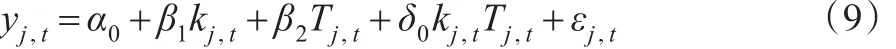
其中,kj,t表示是否参与了西部开发项目,如果是参与组,则kj,t=1 ;如果没有参与,是控制组,则kj,t=0 。Tj,t表示西部开发实施前后的时期,在实施前Tj,t=0,在实施后,Tj,t=1,kj,tTj,t是交互项,用did表示,它的系数反映了西部开发政策在参与组和控制组、参与前和参与后的差异,是政策实施效应的重要体现。采用混合截面数据,利用线性回归方法(OLS),公式(9)的估计结果见表2。
为了分析控制变量对国内经济增长的影响,在公式(9)的基础上,增加控制变量,这样双重差分模型就变为:
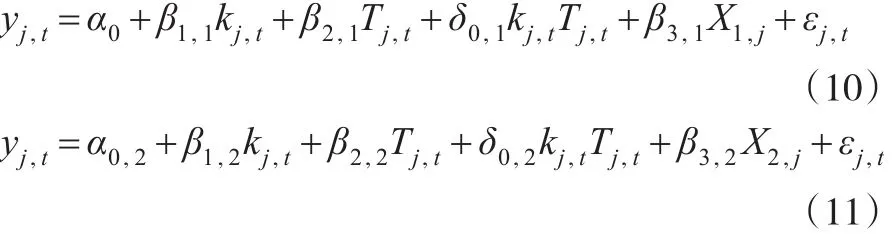
其中,X1、X2分别代表控制变量采掘业从业人员占比、采掘业固定资产投资占比。这两个变量反映了资源开发的能力,是资源开发的替代变量。
2.2 模型估计结果
运用Stata.12采用xtreg命令,利用VCE(r)调整异方差和序列相关,对公式(9)至公式(11)进行估计,回归结果见表2。
表2中,多元线性回归(a)显示DID项显著影响各省份的国内生产总值增长速度,表明西部大开发政策的效果是显著的,西部大开发政策促进了西部国内生产总值增长(δ0=0.0511)。大开发的政策效应促使西部国内生产总值相对非西部开发省份提速5.11%。检测中,P值等于0.005,达到1%的显著水平。西部开发政策效应在政策实施前后,控制组(西部开发省份)和干预组(非西部开发省份)之间的差异达到了5.11%。在政策实施前,干预组的国内生产总值增长速度低于控制组,而政策实施后,干预组的国内生产总值增长要比控制组高,这种影响是显著的。
DID变量正的系数值说明西部地区国内生产总值增长水平要比非西部地区高4.66~5.11个百分点,这种差别是西部开发战略所引起的,双重差分检测的结果是西部开发政策的净效果,并且排除了其他影响因素。
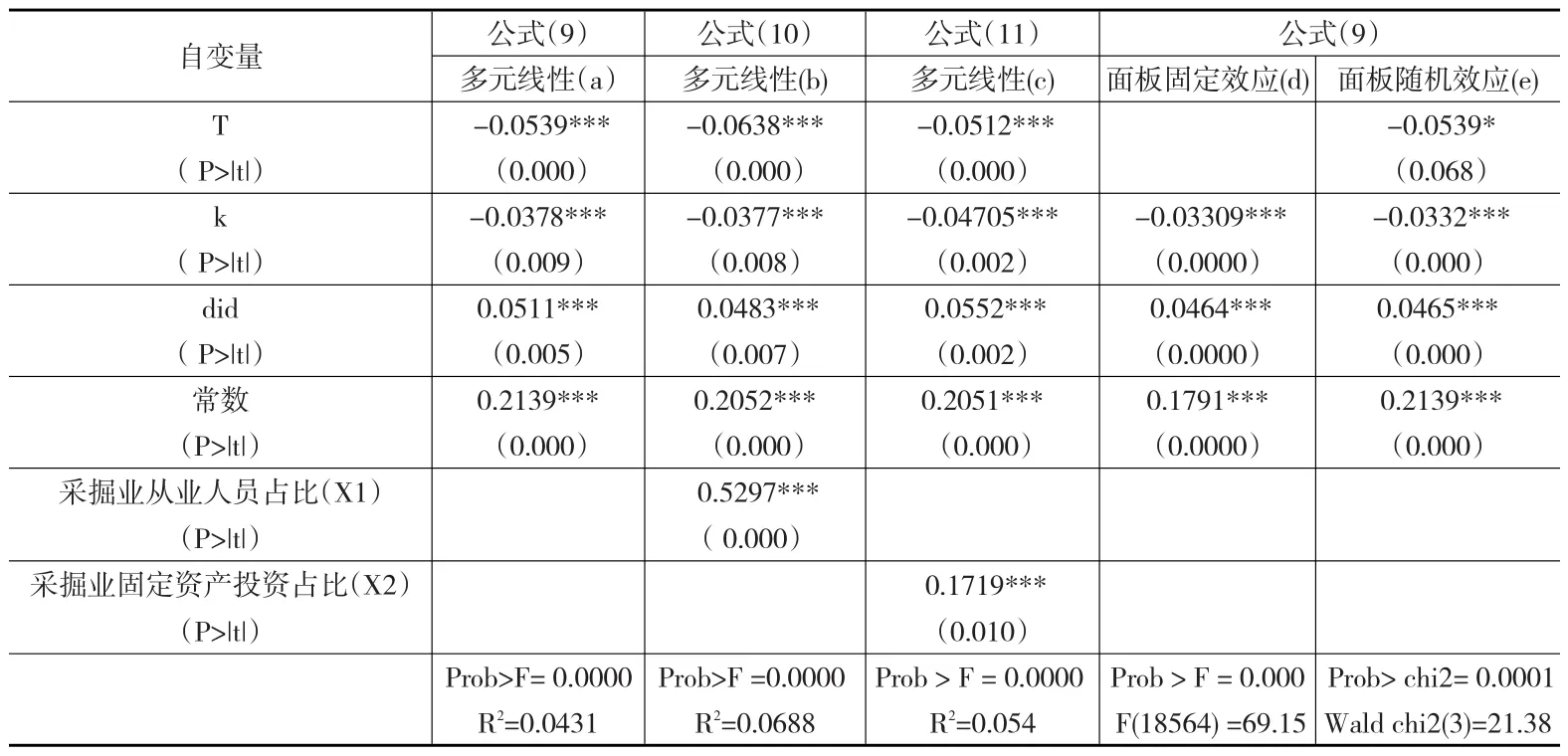
表2 西部开发政策影响经济增长的双重差分模型

表3 双重差分的时间效应与政策效应
为了分析资源诅咒是否成立,本文利用双重差分方法,进行检验。选取两个代表资源开发情况的变量(采掘业从业人员占比、采掘业固定资产投资占比)这两个变量反映了采掘业发展能力状况。这两个变量通过双重差分多元线性回归检验,发现两个变量显著影响国内生产总值增长速度,但是从影响的方向看,资源替代变量增加,导致国内生产总值增长速度增加,说明资源诅咒效应不存在。徐康宁,王剑(2006)检验发现,自然资源支持了中国经济的高速增长。公式(10)采用采掘业从业人员占比,公式(11)采掘业固定资产投资占比。两个模型的分析结果相同,资源诅咒效益不明显。夏飞等(2014)在对资源禀赋较好的中国西部省份进行检测,发现西部地区资源并没有显著影响经济增长,但是也没有发现资源对国内生产总值增长有显著作用。本文中,多元线性回归模型(b)、(c)显示资源替代变量会显著增加国内生产总值增长,这样的结果否定了资源诅咒效应在省域层面的存在,同时肯定了资源对国内生产总值增长的促进作用。
公式(10)多元线性回归(b)和公式(11)多元线性回归(c)的双重差分的政策效应为正值(分别为0.0483和0.0552),表明政策实施后提升了西部省份的国内生产总值增长速度。
2.3 模型稳健性检验
为了反映模型的稳健性,采用模型替代方法,根据综列数据,利用面板随机效应对模型进行进一步检验。为了检验多元线性双重差分的稳健性,利用面板回归进行分析。对公式(9)进行固定效应模型和随机效应模型进行分析(分析结果见表2(d)和(e)),模型的显著性没有发生改变,说明公式(9)双重差分分析稳健性较好。
公式(10)和公式(11)的面板回归(f)、(g)、(h)、(k)中,资源诅咒效应的回归系数为正值,促进国内生产总值增长(见表4)。这与夏飞等(2014)的研究结果相符合,夏飞的研究结果认为省域层面,资源诅咒效应不明显,他们的检测结果显示资源正向影响经济增长,资源诅咒效益不明显。本文中,公式(10)的面板随机效应中,采掘业从业人员占比回归系数为0.1062,可以提升经济增长速度,资源诅咒效应不明显,但是检验的显著性不强,P>|t|=0.219。
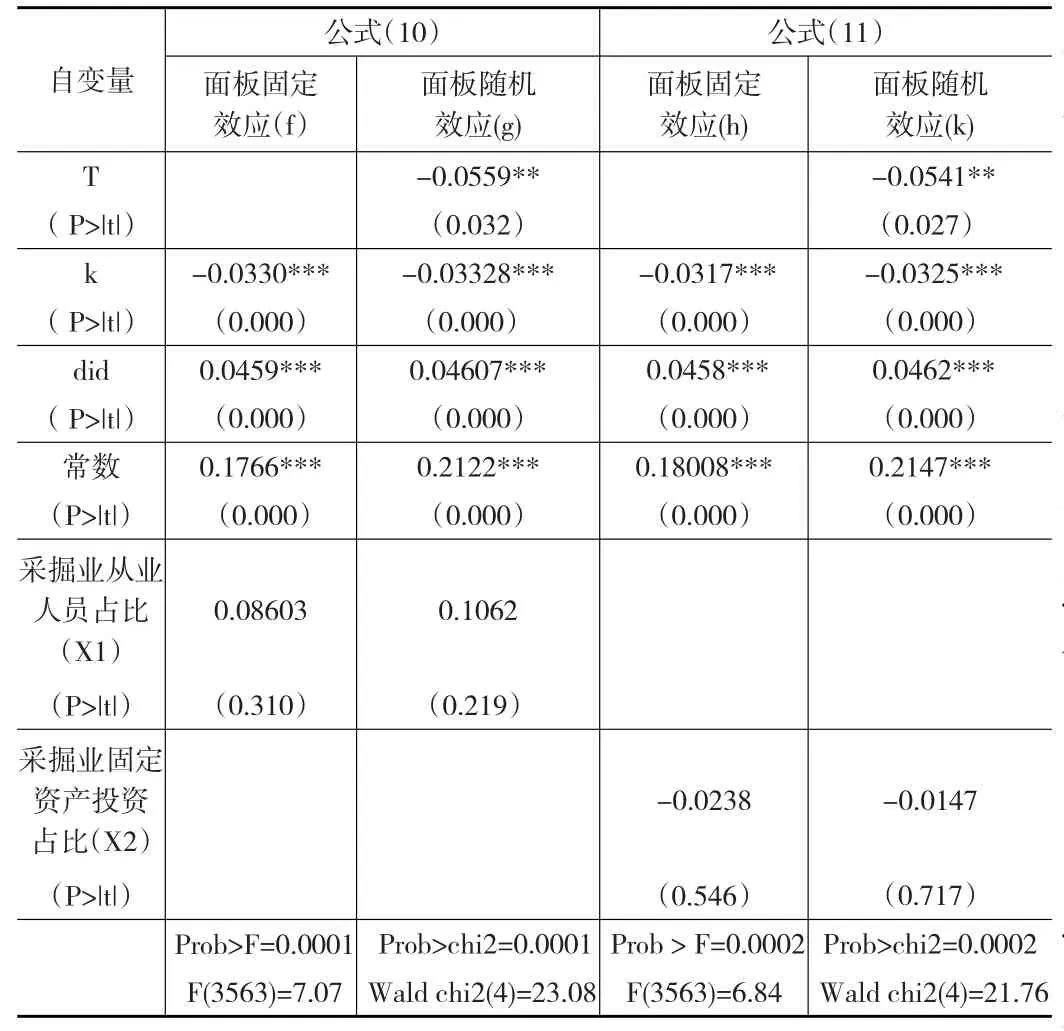
表4 西部开发政策影响经济增长的双重差分模型
3 资源强度的双重差分分析
为了分析资源强的省份和资源弱的省份在西部大开发前后,是否在资源诅咒困境方面进行了改善,本文设置了资源开发强度变量,建立影响经济增长的双重差分模型,资源开发强度参照国内外的研究,选取采掘业固定资产投资规模占全社会固定资产投资规模的比重。设置虚拟变量H,表示资源开发强度,资源开发强度(采掘业固定资产投资规模占全社会固定资产投资规模的比重)排名在前15的取值为1,表示资源开发高强度,资源开发强度排名在后16位的取值为0,表示资源开发低强度。设置时期变量T,在西部大开发前,取值为0;西部大开发之后的,取值为1。那么双重差分模型为:
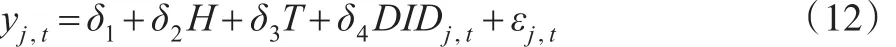
交互项DIDj,t的系数δ4表示在西部大开发中,资源开发强度高的省对经济增长的影响。
利用1993—2011年的各省份数据,采用线性回归和面板回归两种方法进行分析。分析结果见表5。

表5 采掘业开发强度影响经济增长的双重差分模型
公式(12)的多元线性回归分析结果表明,资源强度显著影响国内生产总值增长,DID项为0.03644,资源开发强度促进国内生产总值增长。夏飞等(2014)通过设置资源强度,进行双重差分检验发现,西部大开发战略使得资源富集的省份的经济增长速度要比资源匮乏的省份高1.17~1.63个百分点。并且认为大开发战略有利于缓解环境资源诅咒困境。本文的检测也证实了以上观点,本文的双重差分检验发现,西部大开发战略,导致资源富集的省份的国内生产总值增长速度要比资源匮乏的省份高3.6~3.9个百分点。

表6 资源强度双重差分的时间效应与政策效应
从表6的双重差分的时间效应和政策效应看,政策实施前,干预组的国内生产总值增长速度低于控制组。政策实施后,政策的干预效应(δ4=0.03644)为正值,政策促进了西部地区的国内生产总值增长。西部开发政策,对于资源强省的影响也是显著的,由于资源强省分布主要集中与西部,资源强度双重差分分析也验证了西部开发政策能促进国内生产总值增长。
4 结论
本文通过双重差分方法检验西部大开发政策对西部经济增长的影响,同时也检验西部开发中,资源诅咒效应是否存在。检验结果发现,从我国省域层面看,资源诅咒现象不明显,而资源对国内生产总值增长的促进作用明显。从以往的文献分析中发现,在西部大开发之前西部地区资源与经济增长呈负相关关系,从而资源诅咒现象存在,而本文的研究通过双重差分研究西部开发前后,资源对经济增长产生正向影响。从政策制度对资源诅咒的影响关系看,西部开发政策对国内生产总值具有促进作用,效果显著,而资源对国内生产总值呈现正相关关系,促进作用显著,并没有出现资源诅咒限制经济增长的趋势。
运用双重差分模型分析发现,西部地区在西部大开发政策实施后,国内生产总值增长速度比非西部地区高,也说明西部大开发战略缓解西部地区的资源诅咒困境,西部地区的经济增长速度加快,缩小了与非西部地区的差距。
