面板数据模型基于Within估计的最优设计

程 靖,岳荣先，王 萍

（1.安徽农业大学 理学院，合肥 230036；2.上海师范大学 数理学院，上海 200234）

0 引言

面板数据模型是一类在经济学、心理学、管理学等科学领域中应用较为广泛的随机系数回归模型[1]。由于随机效应项的存在，很难获得该模型中未知回归系数的最佳线性无偏估计。常见的解决方法有两种：一种方法是构造回归系数的两步估计[2]；另一种方法是设法构造回归系数不含有未知参数的估计量[1]，其中Within估计是在计量经济学中应用广泛、影响深远的一种估计量。由于消除了不可观测的随机个体效应，Within估计量中不再包含未知参数，并具有无偏性和一致性等优良性质，同时它也是由面板数据模型衍生的一个子模型中未知参数的最佳线性无偏估计。

在统计模型中，未知参数估计的精度会依赖于收集数据的试验设计方案。目前有关包含多个随机效应的随机系数回归模型最优设计的研究[3-6]都将随机效应项的方差视为已知，而获得的最优设计通常都是依赖于随机效应项的方差比值，这在实际中较难实现。程靖和岳荣先[7]讨论了单位正方形设计域上含有两个解释变量的面板数据基于Within估计的几类最优恒等设计，得到了不依赖于随机效应项方差的最优设计。由于随机系数回归模型中最优设计的结论并不能从单位设计域直接应用到一般设计域上，本文将尝试对相应结论进行一般化推广，考虑该模型在矩形设计域[a，c]×[b，d]上基于Within估计的最优恒等设计。本文首先证明了含有两个解释变量的面板数据模型在任意矩形设计域[a，c]×[b，d]上基于Within估计的最优恒等设计可以在 (a，b)，(a，d)，(c，b)，(c，d)四个顶点上获得，并进一步证明了在对称的矩形设计域四个顶点处的等权重设计是该模型基于Within估计D-、A-和I-最优设计。

1 面板数据模型的Within估计

面板数据模型可表示为：

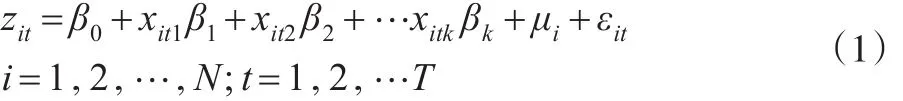
上式中zit表示第i个观测对象在t时刻的观测结果；xitj表示第i个观测对象上第j个解释变量在第t个观测时刻的取值；β1，β2，…，βk为待估回归系数；μi～N(0，σμ2)是第i个个体的随机效应，εit～N(0，σ2)是随机误差，这里σμ2和σ2是未知参数。假定所有的随机个体效应μi和随机误差εit互不相关。引入记号：

则上述模型（1）可简化为：

上式中1NT表示元素全部是1的NT维列向量，IN表示N阶单位阵，⊗表示Kronecker乘积。易见：

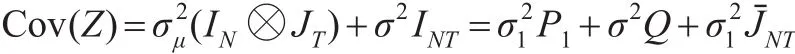
容易证明上式中的矩阵JˉNT，P，Q，P1均为对称幂等阵，且这些矩阵是两两相互正交的。在面板数据模型（2）两侧同时乘对称幂等阵Q，得到：

易得模型（3）中未知回归系数β的BLUE（最佳线性无偏估计）是：

由式（4）所表示的估计量就称为面板数据模型（2）中未知参数β的Within估计，并有：

2 最优设计

本文将对程靖和岳荣先[7]中的结论进行进一步推广，

考虑含有两个解释变量的面板数据模型在一般矩形设计域[a，c]×[b，d]上基于Within的最优恒等设计。为了简便起见，下文中对含有两个解释变量的面板数据模型改用如下记号：

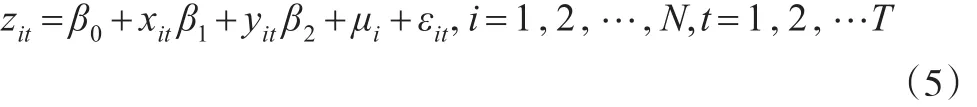
其中 (xit，yit)∈[a，c]×[b，d]。大多数实际情况下，不同单元的观测的时刻和解释变量的指标选取往往相同，即对 ∀i，j=1，2，…，N，xit=xjt，yit=yjt。本文也仅考虑此类恒等设计中的近似最优设计。记恒等设计:

其中可以看出Within估计的协方差阵中的未知参数σ2对设计方案的选择没有影响，不失一般性，这里假定σ2=1。则在近似恒等设计（6）下模型（5）基于Within估计的信息阵可以表示为：

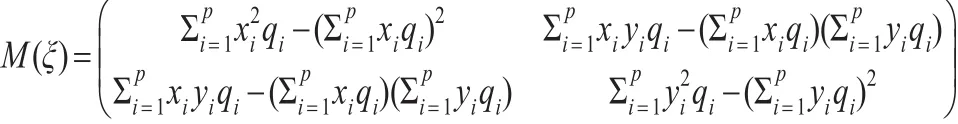
由此可以推出下述结论：

定理1：考虑含有两个解释变量的面板数据模型（5）基于Within估计的恒等设计，那么对设计域[a，c]×[b，d]上任一形如式（6）的近似设计，存在一个支撑点在设计域四个顶点上的近似设计：

满足M(ξ͂)≥M(ξ)。

证明：令：

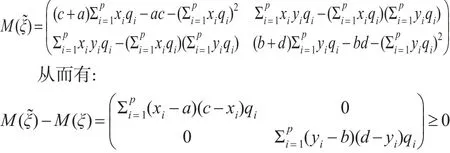
即M(ξ͂)≥M(ξ)。

经典的D-、A-和I-等最优设计准则的准则函数均具有Loewner偏序性质[8]，即对两个设计ξ1，ξ2的信息阵，如果M(ξ͂)≥M(ξ)都有 Φ(M(ξ1)) ≤Φ(M(ξ2))。由于最优设计就是寻找使得信息阵的准则函数达到最小的设计，因此结合定理1的结论可知：对于由式（5）所描述的面板数据模型，其基于Within估计的最优恒等设计可在形如式（7）的设计类中获得。在恒等设计（7）下:

其中：

对于确定的设计域，可以通过优化上述信息阵的准则函数来获得最优设计的解析或数值结果。本文是对其中的某一些或某一类设计域能够获得具有优良性质的最优设计。下面仅考虑面板数据模型（5）在对称设计域[-h，h]×[-l，l]上基于Within估计的最优恒等设计。由定理1可知最优设计形式如下：

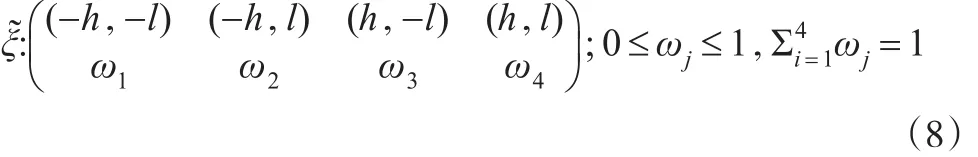
这里信息阵满足：

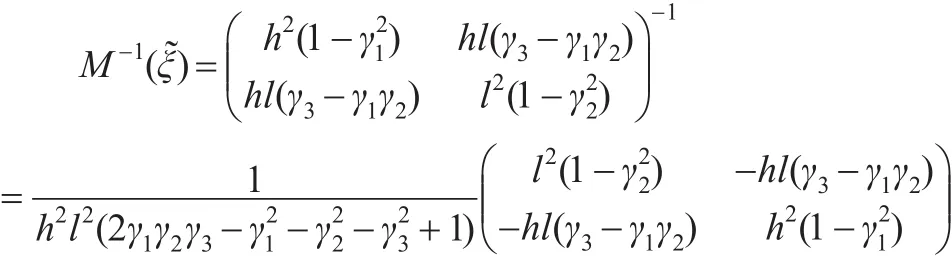
其中γ1=ω3+ω4-ω1-ω2，γ2=ω2+ω4-ω1-ω3，γ3=ω1+ω4-ω2-ω3。综合ωj的取值范围及设计点的个数不能少于2个可得-1＜γi＜1，i=1，2，3。

恒等设计（8）下，信息阵的D-最优设计准则函数为:

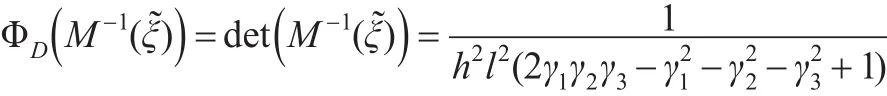
对上式分别关于γi，i=1，2，3 求偏导，并令偏导值为0，可得：

当γ2=γ3=γ1=0,即时，即ΦD(M-1(ξ͂)) 取得极小值。故有定理2。

定理2：考虑含有两个解释变量的面板数据模型（5）基于Within估计的恒等设计，则该模型在设计域[-h，h]×[-l，l]上的D-最优设计为四个对称顶点处的等权重设计：

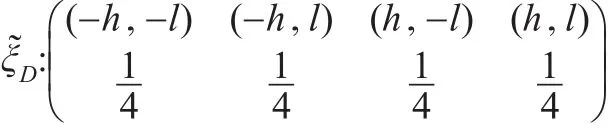
恒等设计（8）下，信息阵的A-最优设计准则函数为：

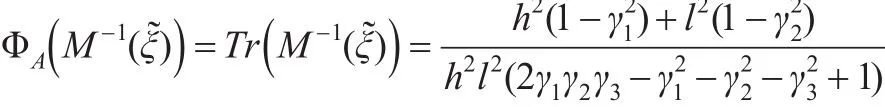
对上式分别关于γi，i=1，2，3 求偏导，令偏导值为0，可得：

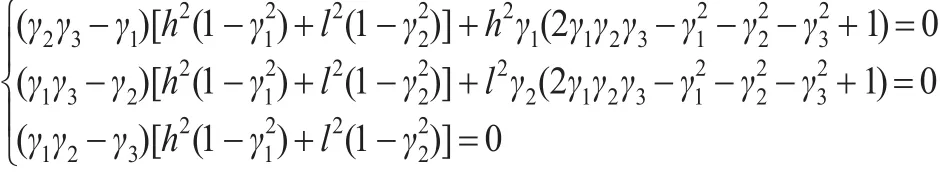
当γ2=γ3=γ1=0,即ω1=ω2=ω3=ω4=时 ，ΦA(M-1(ξ͂))取得极小值。从而有定理3。

定理3：考虑含有两个解释变量的面板数据模型（5）基于Within估计的恒等设计，则该模型在设计域[-h，h]×[-l，l]上的A-最优设计为四个对称顶点处的等权重设计：

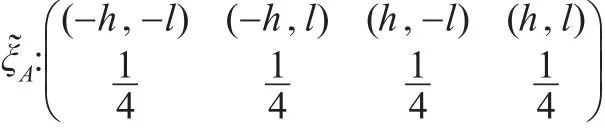
恒等设计（8）下，信息阵的I-最优设计准则函数为：

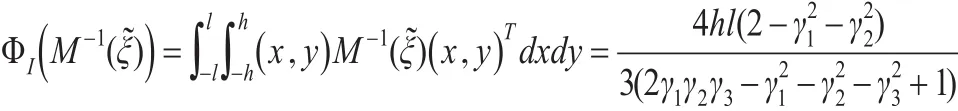
对上式分别关于γi，i=1，2，3求偏导，令偏导值为0可得：

同样可得当γ2=γ3=γ1=0 ，即时，ΦI(M-1(ξ͂)) 取得极小值。故有定理4。

定理4：考虑含有两个解释变量的面板数据模型（5）基于Within估计的恒等设计，则该模型在设计域[-h，h]×[-l，l]上的I-最优设计为四个对称顶点处的等权重设计：

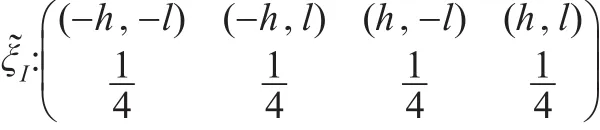
3 结论

本文对含有两个解释变量的面板数据模型（5）最优设计的结论进行了推广，证明了在矩形设计域上考虑该模型基于Within估计的最优恒等设计时，仍可以将最优设计的寻找限定在设计域的顶点处。特别地，如果设计域为对称的矩形区域，可直接采用设计域四个顶点上的等权重作为设计方案，此时等权重设计同时具有D-、A-和I-最优性质。