中国大学评价体系相关性和稳定性的统计学检验
2018-12-21李兴国赵晓冬
李兴国,赵晓冬
(燕山大学a.经济管理学院;b.高等教育发展研究中心,河北 秦皇岛 066004)
0 引言
大学排名作为高等教育发展过程中的一种全球性现象,近年来引起了人们的广泛关注。自1987年《科技日报》刊载了由中国管理科学研究院对国内87所重点大学的排名后,对我国大学排行的研究开始兴起。此后20年间,先后有20余家机构发布了近百个大学排行榜[1]。当前国内影响力较大的大学排行榜主要有三个:武书连大学评价课题组发布的《中国大学综合评价》(简称“武书连榜”)、中国校友会网发布的《中国大学学科专业评价报告》(简称“校友会榜”)、武汉大学中国科学评价研究中心邱均平课题组发布的《中国大学竞争力排行榜》(简称“邱均平榜”)。这三个大学排行榜的排名结果之间是否具有一定的相关性,三大排行榜历年排名数据的稳定性如何?这是本文所要研究的问题。
1 中国大学评价体系简介
武书连榜是由广东管理科学研究院发布的,该课题组从1993年成立至今共发布25个大学排行榜。自1997年开始,该课题组在《科学学与科学技术管理》杂志按年度发表《中国大学评价》,并于2010年4月首次将排行榜评价指标体系公开发表。中国校友会网大学研究团队自2003年起至今已连续15年开展中国大学评价研究,每年发布《中国大学评价研究报告》,是国内唯一以校友、质量、影响为主题特色的中国大学排行榜。武汉大学中国科学评价研究中心2004年首次发布中国大学竞争力排行榜一直延续至今,影响力日益增强[2]。国内三个大学排行榜指标构成如表1所示。
2 研究方法
2.1 Pearson相关检验
相关关系是不完全确定的随机关系,连续变量之间的相关系数常用Pearson相关系数来测定,两个连续变量X和Y之间Pearson相关系数的计算公式为:
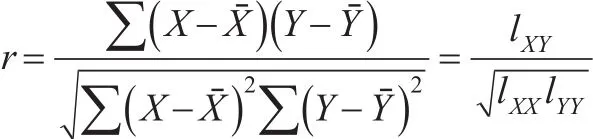
r的取值在-1和1之间,r值与变量相关程度之间的关系如表2所示。

表2 |r|的取值与相关程度
2.2 Kendall秩检验
Kendall秩相关系数是利用变量的秩进行变量之间的一致性趋势检验。假设有容量为n的由x和y两个变量构成的随机样本,首先计算每个观测变量关于变量x和y的秩变量u和v,将n个观测变量按变量x升序排列。则n个观测关于变量x和y的秩为[3]:x的秩变量u:1,2,…,n;y的秩变量v:v1,v2,…,vn。
设在v1的后面有R1个秩大于v1,在v2的后面有R2个秩大于v2,…,在vn-1后面有Rn-1个秩大于vn-1,令:R=R1+R2+…+Rn-1,显然,变量x和y相关性越强,则R越大。
Kendall秩相关系数的计算公式如下:
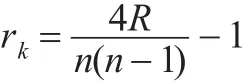
Kendall秩相关系数的绝对值不超过1。
2.3 Wilcoxon符号秩检验
定序变量配对样本间的相关性常用Wilcoxon符号秩检验,Wilcoxon检验利用两个配对组的数值之差进行检验。求出数值差之后,按照绝对值由小到大对这些差值排序。计算最小的秩和,记为T。如果样本配对数目n≤15,则直接将T值与查表得到的临界值比较[3]。如果n>15,则T值近似服从正态分布,可以用z分数作为检验统计量。检验统计量为:为配对数目,T为正值差的秩或负值差的秩中的较小者[3]。
2.4 Friedman检验
Friedman检验是M.Friedman于1937年提出的,它是随机化区组设计的非参数替代技术。随机化区组设计的假定与其他ANOVA分析的假定一样,即观察值是从正态总体中随机抽取的。如果不满足这个假定,或研究对象是排序数据,则应采用Friedman检验。Friedman检验有三个基本假定:一是区组相互独立;二是区组与处理之间没有交互效应;三是各区组内的观察值可以进行排序[4]。
待检验的假设如下:H0为处理总体相同;H1为至少有一个处理总体不同。
进行Friedman检验时,首先把原始数据转换为排名。Friedman检验是在每个区组内分别从1到c进行排序。每个区组都有c个排名,其中c是处理水平数。利用这些排名,Friedman检验可以判断不同的处理水平(列)是否来自同一个总体。Friedman检验所用的检验统计量见公式(1),该统计量近似服从卡方分布,如果c>4,或c=3且b>9,或c=4且b>4,则自由度为df=c-1。
Friedman检验的统计量为:
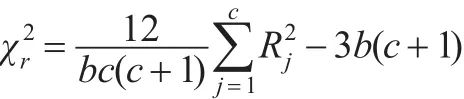
其中,c为处理水平(列数),b为区组(行)数,j为特定处理水平,≈χ2,df=c-1,Rj为特定处理水平(列)的秩和。
3 实证分析
本文选取2010—2017年38所“985工程”高校(不含国防科技大学)在武书连榜、校友会榜和邱均平榜中的排名数据[5-7],对三个中国大学排行榜的数据进行相关性和稳定性检验。
3.1 大学排行榜自身稳定性检验
分别计算38所“985工程”高校在三个大学排行榜中2017年的排名与之前七年排名的Pearson相关系数,结果如表3所示。可见,三个大学排行榜2017年排名与前七年排名数据具有较强的相关性,相关系数的均值都在0.8以上,属于高度相关,且显著性检验的P值均近似为零,在0.01的水平上显著相关,这表明三个排行榜历年排名数据具有较高的稳定性。其中,武书连榜的相关系数均值最高,为0.8974;其次为邱均平榜,相关系数均值为0.8587;校友会榜相关系数的均值相对最低,为0.8199。
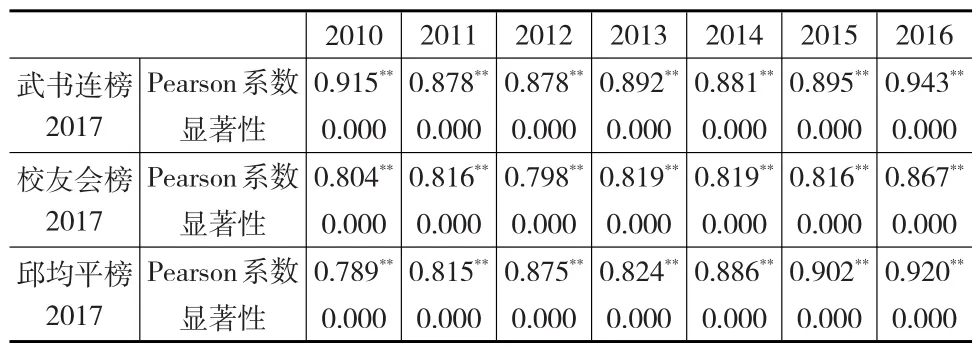
表3 国内三个大学排行榜数据的相关性检验
根据三个大学排行榜近八年排名数据之间的相关系数值,绘制出三个排行榜2017年数据与2010—2016年数据的相关趋势图,如图1所示。可见,历年来武书连榜的相关系数值最高,每年均在0.85以上,且呈现出逐年上升的趋势。邱均平榜历年来的相关系数值变化幅度最大,尤其是2013年相关系数骤降,2014年又大幅回升,之后逐年上升;校友会榜历年的相关系数基本上在0.8~0.85之间。值得注意的是,校友会榜相关系数的变化趋势曲线与武书连榜高度一致,而多数年份邱均平榜相关系数的变化趋势与其他两个排行榜则相反。总体上,三个排行榜近八年排名数据的相关系数均呈现逐年上升的趋势。
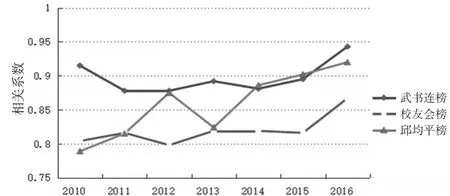
图1 三个中国大学排行榜2017年数据与2010—2016年数据的相关趋势图
3.2 三个排行榜之间的相关性检验
为了检验三个大学排行榜彼此排名数据之间的相关性和一致性,首先计算“武书连榜-校友会榜(W-X)”、“武书连榜-邱均平榜(W-Q)”、“校友会榜-邱均平榜(X-Q)”2010)—2017年间各年排名数据的Pearson系数和Kendell系数值,结果见下页表4。可见,三个大学排行榜之间的数据呈现出较高的相关性,且在0.01的水平上显著相关。其中,校友会榜和邱均平榜排名数据之间的相关性最强,相关系数的均值高达0.95,为极高相关;其次为校友会榜和武书连榜之间的相关系数,也高达0.89;武书连榜和邱均平榜之间的相关系数相对而言最低,但也达到了0.85,属于高度相关。
其次,根据下页表4中的Pearson相关系数,绘制出三个大学排行榜2010—2017年排名数据彼此之间相关性趋势图,如图2所示。由图2可知,“校友会榜-邱均平榜(X-Q)”和“武书连榜-邱均平榜(W-Q)”呈现出高度一致的变化趋势:2012年前相关性趋强,2013年相关性骤降,2014年降至谷底后反弹,2015年后相关性又逐年趋强。“武书连榜-校友会榜(W-X)”的相关性则始终保持平稳增长的趋势。从相关系数的振幅看,“W-X”之间的振幅最小,“X-Q”之间的振幅居中,“W-Q”之间的振幅最大。
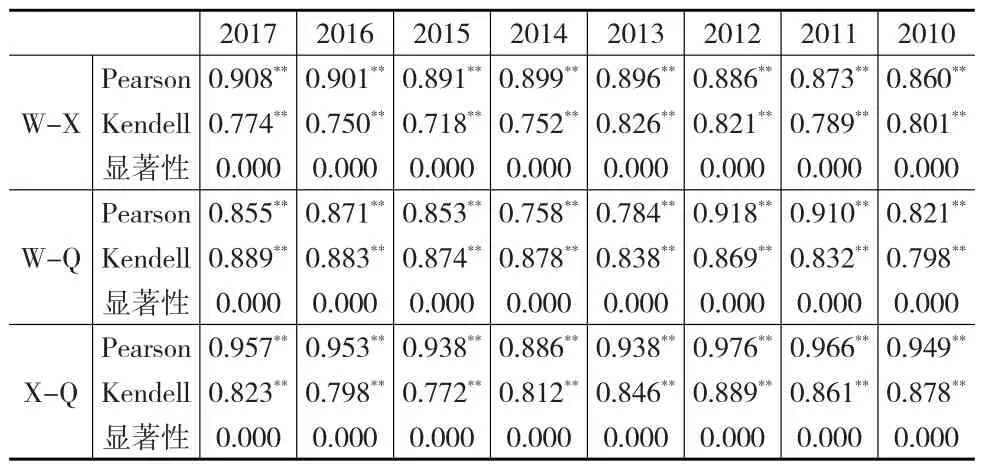
表4 国内三个大学排行榜之间数据的相关性与一致性检验
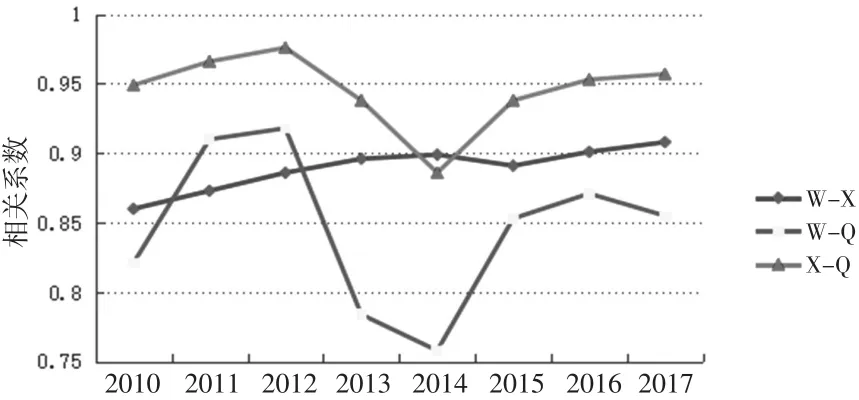
图2 2010—2017年三个中国大学排行榜排名数据相关性趋势图
最后,根据表4中不同排行榜历年来的Kendell一致性系数,绘制出三个大学排行榜2010—2017年数据彼此之间一致性趋势图,如图3所示。“校友会榜-邱均平榜(X-Q)”和“武书连榜-校友会榜(W-X)”的一致性趋势图形状高度吻合,“武书连榜-邱均平榜(W-Q)”的一致性曲线图呈现出不同于另外两条曲线的特征。三条曲线在2013年的一致性系数最为接近,之后则差异越来越大。
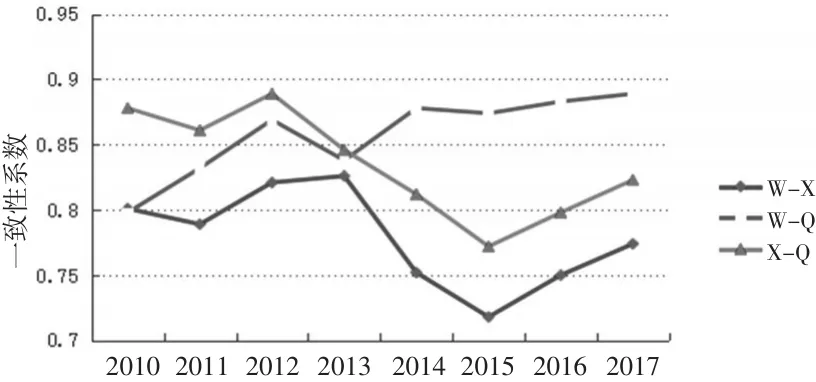
图3 2010—2017年三个中国大学排行榜排名数据一致性趋势图
3.3 三个排行榜之间的稳定性检验
首先,应用Wilcoxon符号秩检验方法,对三个大学排行榜数据进行两两之间的差异性检验,结果如表5所示。检验的P值均大于0.05,没有充分证据表明三个大学排行榜数据之间存在显著差异,即三个大学排行榜的排名数据具有较高的一致性。
然后,分别对三个不同大学排行榜八年的数据做Friedman检验,结果如表6所示。武书连榜的P值高达0.981,邱均平榜的P值为0.607,校友会榜的P值最低,为0.037。P值越高,表明历年大学排名数据变动越小,即排行榜的稳定性越强。可见,武书连榜的稳定性最强(数据具有较强的粘性),其次为邱均平榜,再次为校友会榜。
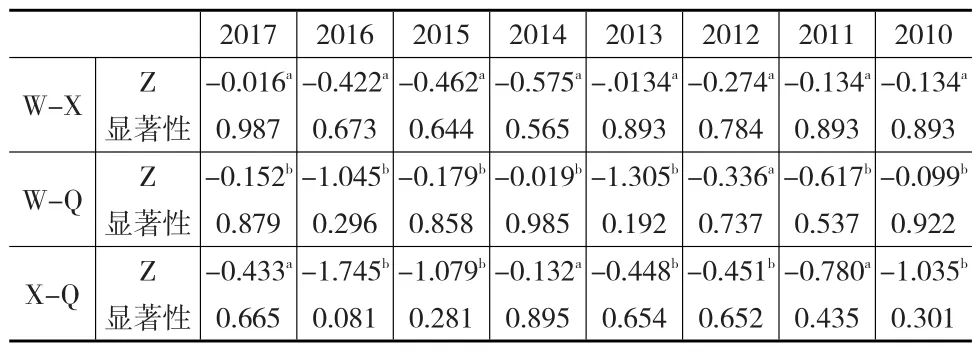
表5 国内三个大学排行榜之间数据的差异性检验
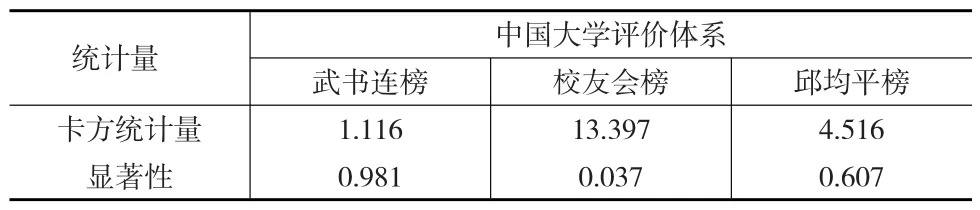
表6 国内三个大学排行榜数据的Friedman检验
4 结论
(1)武书连、校友会和邱均平三个中国大学排行榜数据自身具有较强的稳定性。T年的大学排名数据与T-1年数据的相关性最强,与T-2年数据的相关性次之。依次类推,随着时间的前移,排名数据之间的相关性越来越弱。应当说这种数据特征符合客观事物的发展规律,是中国大学评价体系科学性的体现之一。
(2)三个中国大学排行榜排名数据在0.01的水平上显著相关,两两之间数据的相关系数高达0.85以上。其中,“校友会榜-邱均平榜”之间的相关性最高,“武书连榜-校友会榜”之间的相关性次之,“武书连榜-邱均平榜”之间的相关性相对而言最低。
(3)三个中国大学排行榜排名数据均具有较高的稳定性。其中,武书连榜的稳定性最强,其次为邱均平榜,再次为校友会榜。且没有充分证据表明三个大学排行榜之间存在显著差异,即三个大学排行榜的排名数据具有较高的一致性。
