考虑失效相关性的n部件多型贮备系统可靠性评估优化计算模型

谭启涛，唐家银，邓 川

（西南交通大学 数学学院，成都 611756）

0 引言

贮备一些同型零部件作为重要零部件的备份是工程中为提高系统的可靠性常用的方法之一。当工作部件失效时，转换开关将启动贮备部件瞬时进入工作状态，从而保证系统持续工作。但是贮备部件在贮备期存在性能退化的可能，导致贮备部件的工作寿命产生变化，故而评估该类型系统可靠性是相对困难的。

假设系统由n个部件组成，在初始时刻，一个部件开始工作，其余n-1个部件作贮备，当工作的部件失效时，贮备部件逐个进行替换，直至所有部件寿命终止，系统失效。冷贮备系统是指贮备的部件在贮备期间不失效，贮备对工作时的寿命没有影响。温贮备是指贮备的部件在贮备期也有可能失效，而且贮备寿命分布与工作寿命分布一般不同。

传统的贮备系统研究一般假定工作寿命分布指数型，且部件的寿命相互独立，温贮备系统还假定部件的工作寿命与贮备时间互不影响。显然，此类可靠性计算模型基于的三类条件不能完全适用于实际工况。为此，近年来国内外学者也对贮备系统进行了进一步的研究。但相关文献[1-9]研究的贮备系统可靠度模型，均是在各部件的工作寿命相互独立，贮备期不影响零部件工作寿命的基础上建模。实际中，完全独立的情况是相对理想化的，同一工作体系下部件的先后工作寿命，由于承受共同的外载环境冲击影响，使得各部件的工作寿命存在一定的相关性；温贮备系统中，贮备过程对部件的工作寿命也存在一定的影响，部件的失效率应随着时间t变化；对于机械结构系统而言，部件在长期载荷作用下会呈现性能退化趋势，假定失效率服从偶然失效型的指数分布有失偏颇。

针对以上诸问题，本文从以下方面进行了研究：部件的工作寿命服从一般型分布，不局限于指数分布；考虑转换开关服从0-1分布和连续型分布，并对连续型分布情形进行了两种分类讨论；引入了Copula函数，考虑了部件之间的失效相关性，并给出了Copula函数统计性选择方法；建立了n维冷贮备系统与温贮备系统可靠度优化计算模型。

1 符号说明

Xi：第i个部件的工作寿命，i=1，2，…，n。

Xs：系统的寿命。

Z：转换开关的寿命。

Yj：第j个贮备部件的贮备寿命，j=2，3，…，n。

FXi(xi)：第i个部件的工作寿命的分布函数，i=1，2，…，n。

FZ(z)：转换开关的寿命分布。

FYj(yj)：贮备部件的贮备寿命的分布函数，j=2，3，…，n。

fXi(xi)：第i个部件的工作寿命的密度函数，i=1，2，…，n。

Xi，1，…，Xi，k，…，Xi，i：从X2，…，Xn选出 i个，其中i=0，1，…，n-1 ；k=1，2，…，i。其中i，k表示Xi，k在X2，…，Xn的下标，对于每一个固定的i，存在种不同取法。后文中为了使积分表达式更为简洁，简记：i，0=1和i，(i+1)=n+1 。

I：示性函数。

p,q：p是0-1分布事件发生的概率，q=1-p。

2 Copula定义及相关定理

定义1[10]：n维Copula是一个函数C：[0,1]n→[0,1]，且满足：

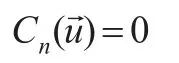
当ui，i≠k，i=1，2，…，n=1，对任意 0 ≤uk≤ 1，则：

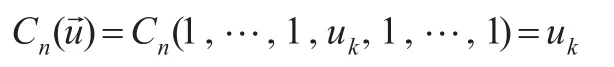
（2）对于 In中任意由的每个分量 ai不大于的对应分量bi）构成的n维盒子，盒子的Copula测度实则是从关于Cn的n阶差分。

定理1[10]：（n维Sklar定理）H(x1，x2，…，xn)是n维随机变量(X1，X2，…，Xn)的联合分布函数，其边际分布分别是F(x1)，F(x2)，…，F(xn)，那么存在唯一的 n维 Copula函数C(u1，u2，…，un)，使得对任意的 (x1，x2，…，xn)∈Rn有：

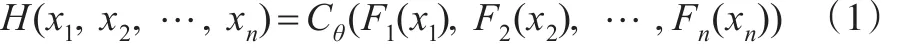
其中θ是相关程度参数，Cθ解析形式因相关结构各异。

3 相关性失效下n部件冷贮备系统可靠度计算模型

对于转换开关完全可靠型冷贮备系统，系统寿命：Xs=X1+X2+ …Xn

当部件的工作寿命 X1，X2，…，Xn不独立时，Xs寿命分布涉及各部件寿命联合密度函数f(x1，x2，…，xn)。X1，X2，…，Xn的相关结构Cθ(u1，u2，…，un)可以通过后续方法，依据样本数据统计拟合得到，由n维Sklar定理，X1，X2，…，Xn联合密度函数：

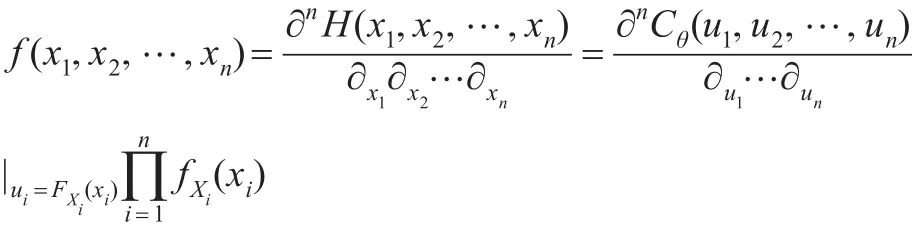
则n部件冷贮备系统的可靠度模型为：

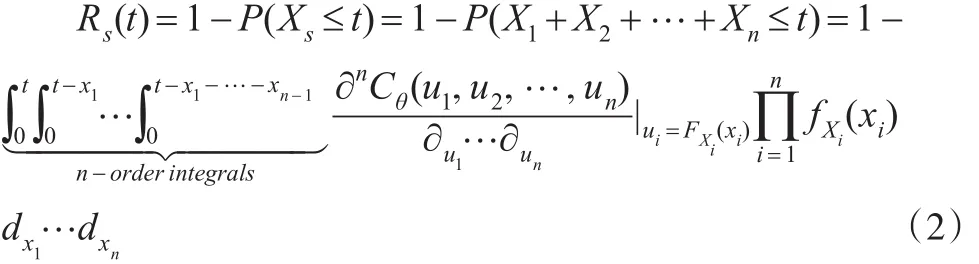
而当转换开关0-1分布型，为了求得系统可靠度，引入随机变量：

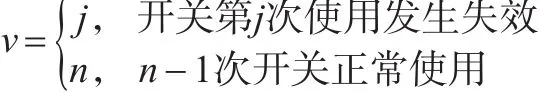
对于该种冷贮备系统，开关正常的概率为p，系统寿命：

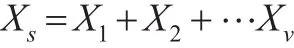
则n部件冷贮备系统的可靠度模型为：

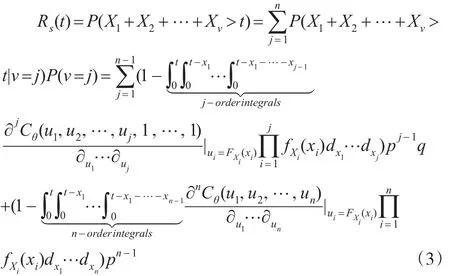
进一步考虑转换开关寿命服从一般连续型分布，开关对系统的影响存在两种情况。

情况一：当开关失效时，系统立即失效。系统寿命为：

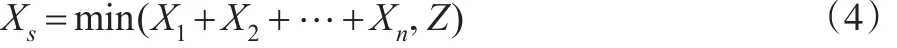
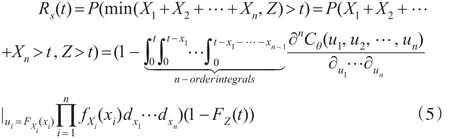
因此该种情况系统可靠度计算模型为：情况二：当开关失效时，系统并不立即失效，当工作部件需要转换开关时，系统由于转换失效而失效。则系统寿命为：

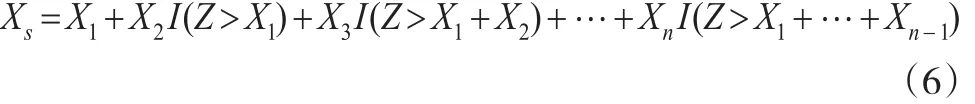
因此系统可靠度计算模型为：

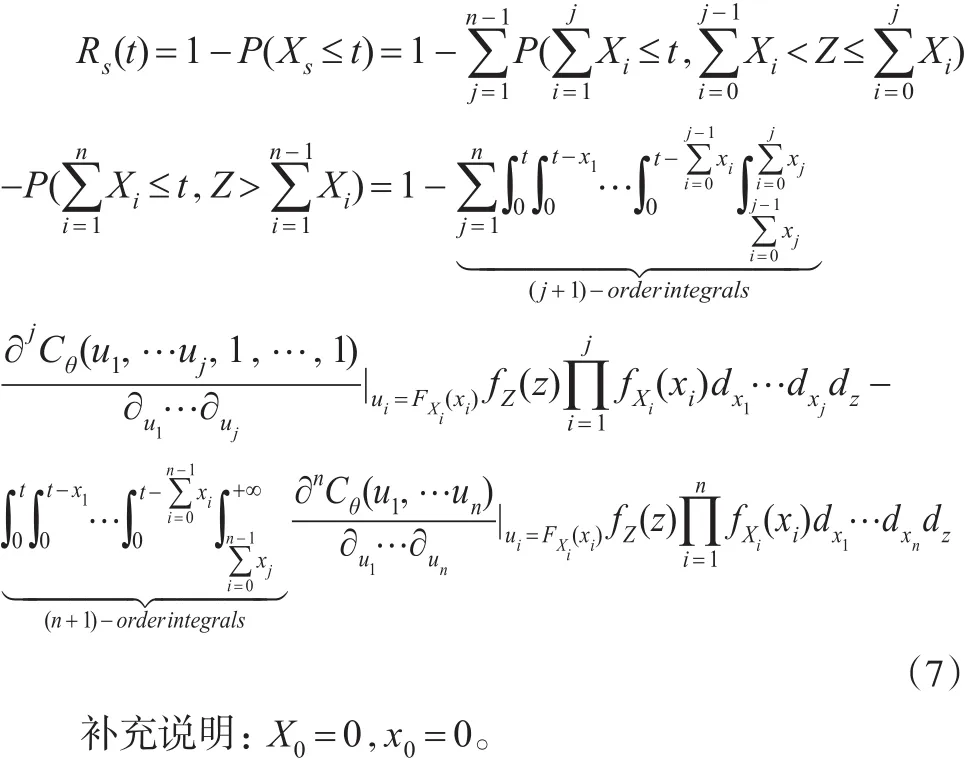
4 相关性失效下n部件温贮备系统可靠度计算模型

4.1 转换开关完全可靠型计算模型

n=3时，考虑Xs的分布函数：

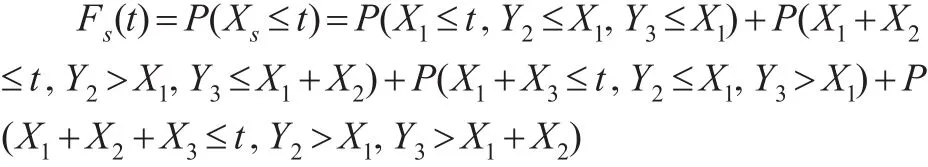
n=4时，考虑Xs的分布函数：

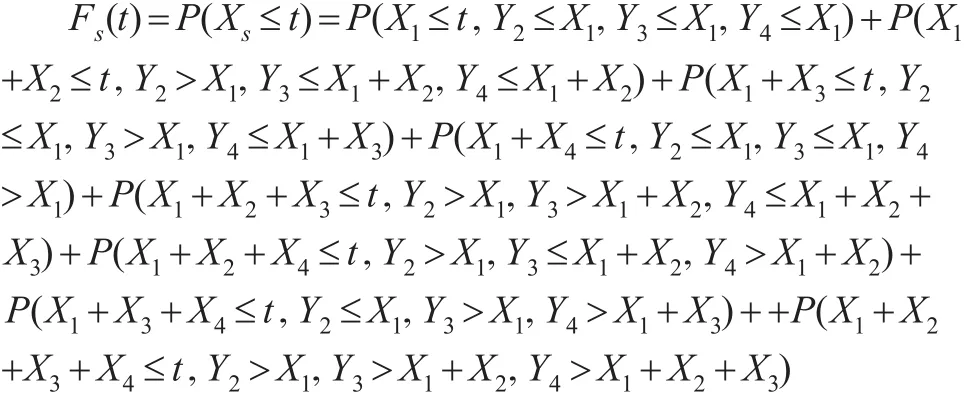
可以看出，温贮备的n-1部件在贮备期都有可能失效，因此系统寿命：

Xs=X1+贮备期未失效部件工作寿命

假设i表示贮备的n-1个部件中未失效的个数，那么系统寿命就会出现种情形，这2n-1种情形是互斥的，那么系统的分布函数即是这2n-1种情形发生的概率之和。

现从n-1个贮备部件中抽取i个，并将抽取出部件记为Xi，1，…，Xi，k，…，Xi，i。则对于每一个 i，存在种不同的取法。其任一种取法可以表示如下：

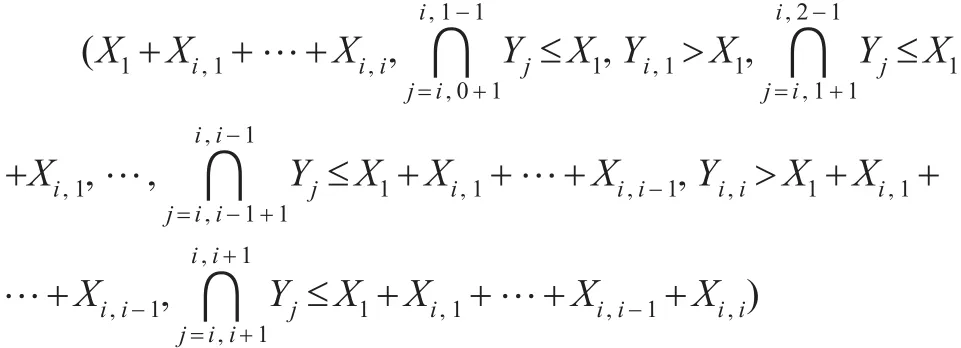
等价于：

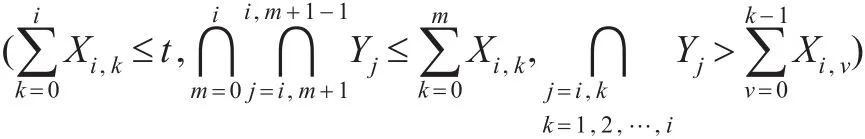
符号“∩ ”表示同时发生。因此该事件发生的概率为：

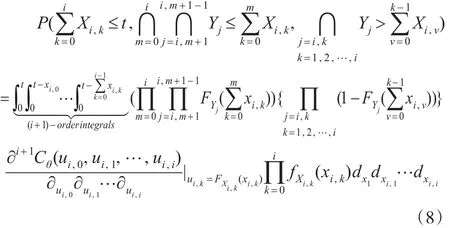
则n部件温贮备可靠度计算模型：

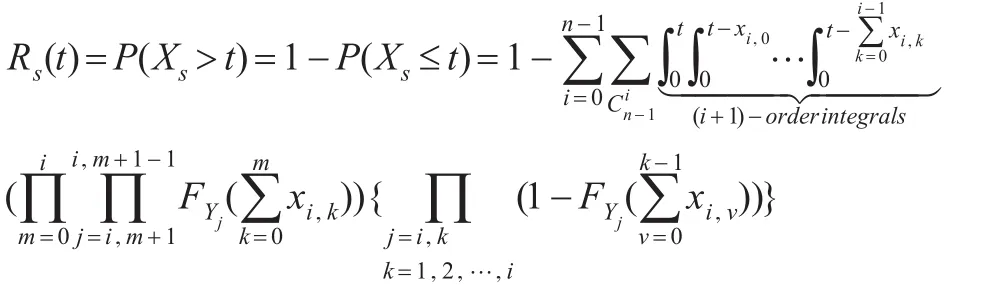
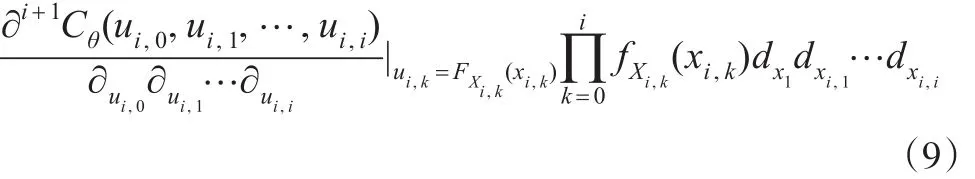
4.2 转换开关0-1分布型计算模型

考虑转换开关时，仍然存在2n-1种互斥的寿命组合，但导致系统失效的原因有两个：①当正在工作的部件失效，需要转换开关时，由于转换开关失效而引起的系统失效；②当正在工作的部件失效，转换开关并未失效，之后的贮备的部件已经全部失效而引起系统失效。但是一定要注意，当任一种寿命组合，如果Xi，i=Xn，那么引起系统失效的原因是由n个部件使用完毕而导致的。

（1）若第n个贮备部件失效，那么共有种情形

现从第2个至第n-1个贮备部件中抽取i个，并将抽取出部件记为Xi，1，…，Xi，k，…，Xi，i。则对于每一个i，存在种取法。其中任一种取法表示为：

因此事件Ai发生的概率为：

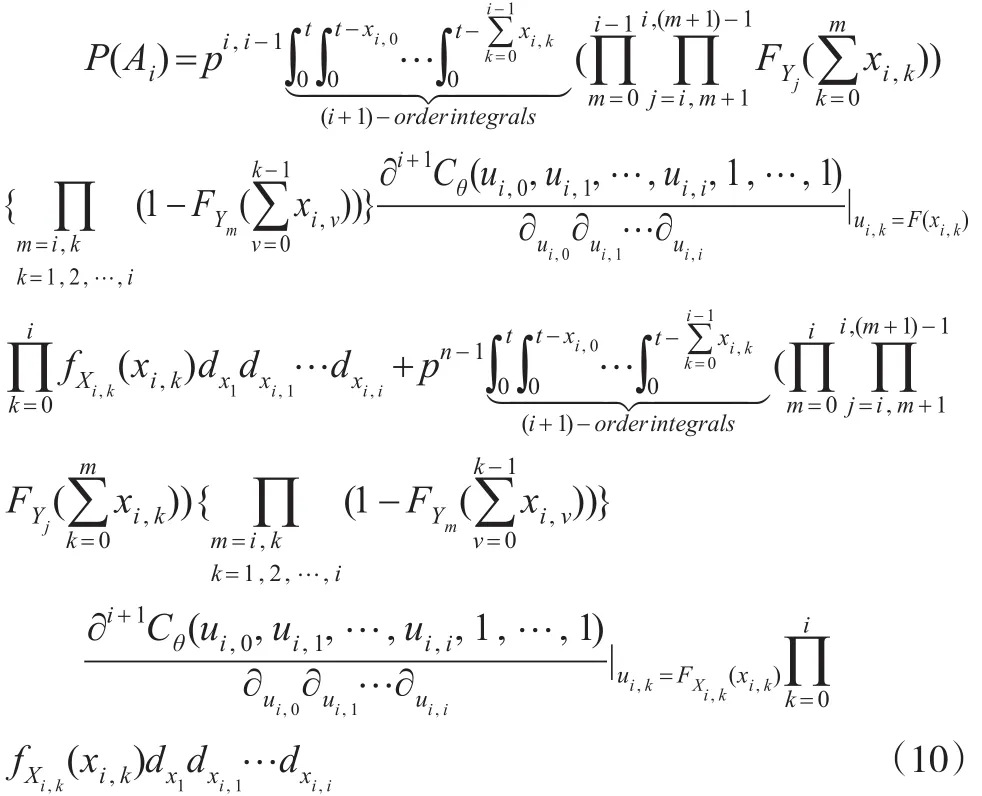
现从第2个至第n-1个贮备部件中抽取i个，并将抽取出部件记为Xi，1，…，Xi，k，…，Xi，i。则对于每一个i，存在种取法。其中任一种取法表示为：开关正常使用了n-1次)

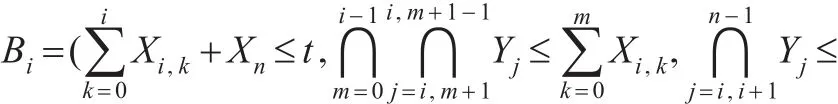
事件Bi发生的概率为：

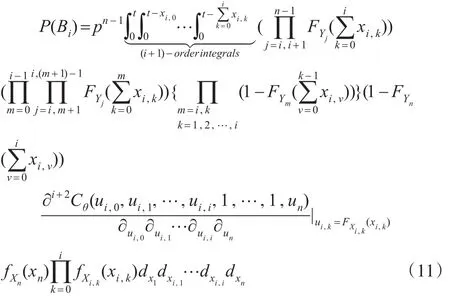
故系统的可靠度计算模型：

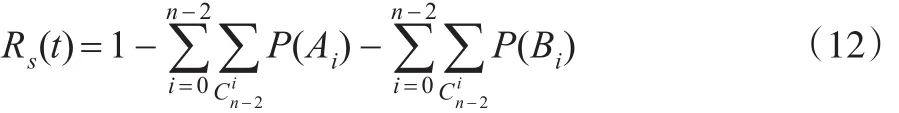
4.3 转换开关连续型计算模型

对于转换开关服从连续型分布的温贮备系统，开关对系统的影响存在两种情况。

情况一：当开关失效时，系统立即失效。

Xs=min(X1+贮备期未失效部件的工作寿命，Z)

因此系统的可靠度计算模型：

情况二：当开关失效时，系统并不立即失效，而需要转换开关时，系统失效。

（1）若第n个贮备部件失效，那么共有种情形

现从第2至第n-1个贮备部件中取出i个，并将抽取出部件记为Xi，1，…，Xi，k，…，Xi，i。则对于每一个i，存在种取法。则任一种取法表示为：

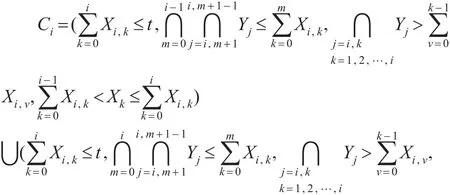
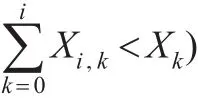
事件Ci发生的概率为：

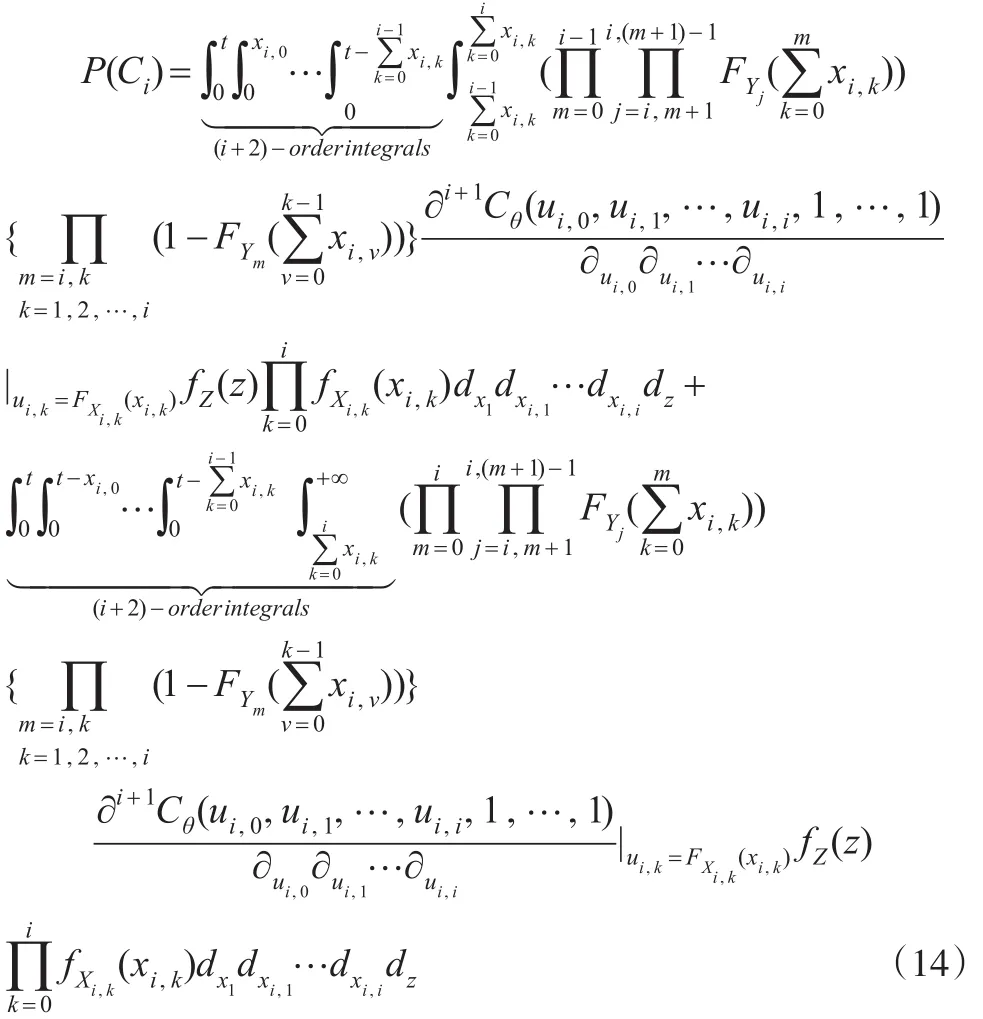
（2）第n个贮备部件未失效，那么共有种情形，此时系统失效的原因一定是n个部件使用完毕而导致的。

现从第2至第n-1个贮备部件中取出i个，并将抽取出部件记为Xi，1，…，Xi，k，…，Xi，i。则对于每一个i，存在种取法。则任一种取法表示为：

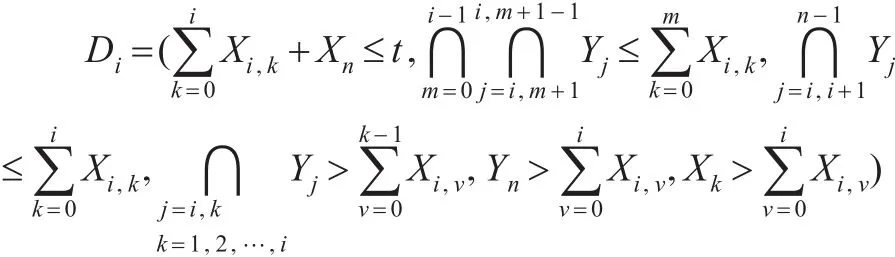
事件Di发生的概率为：

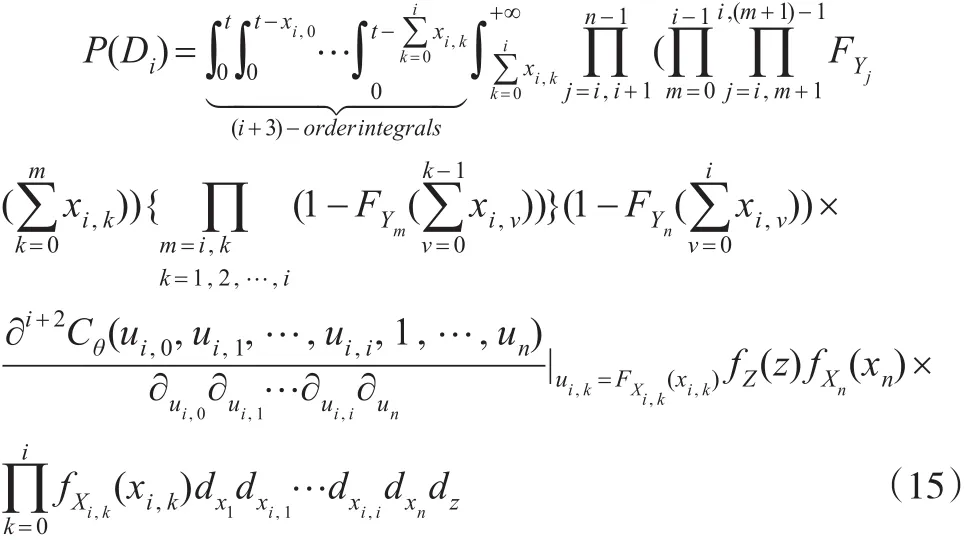
故系统的可靠度计算模型：

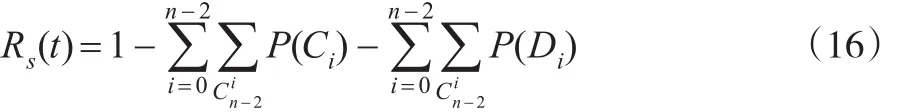
5 相关性的模型统计选择

在工程中，贮备部件的工作寿命受贮备时间的影响，贮备部件的工作寿命会随贮备时间增长而呈现减短趋势。实际中只能获得各部件的工作寿命数据，假设对n个部件构成的系统做了m次观测，获得数据xij，i=1，2，…，m，j=1，2，…，n：

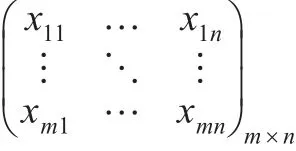
为计算系统的可靠度，需估计部件的工作寿命分布和相关结构进行选择，具体步骤如下：

第一步:由第j，j=1，2，…，n个部件的工作寿命数据xij，i=1，2，…，m，可以估计出各部件的工作寿命分布

第二步:通过观察 (FXi(xt，)，FXj(xt，))散点图，其中t=1，2，…，m，1≤i，j≤n，i≠j，选出符合响应特征的备择Copula函数：Ct(u1，u2，…，un，βt)，t=1，…，k；

第三步:根据每一备择Ct(u1，u2，…，un，βt)，得到对应似然函数：

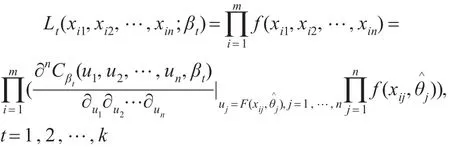
通 过 极 大 似 然 估 计 方 法 ，可 以 估 计 出，t=1，2，…，k；

第四步:将样本数据按列变量排序：

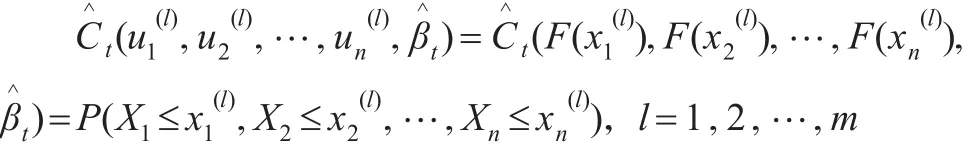
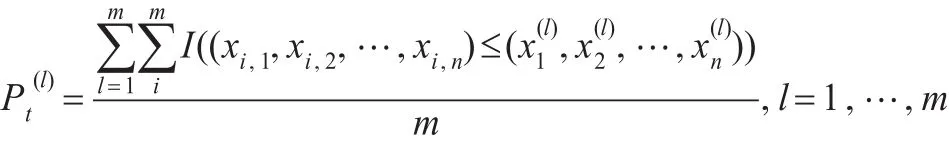
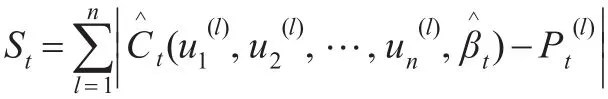
比较St，选择使St最小的

6 算例

一台发动机关于工作时间t（单位：h）的故障率λ1(t)=0.002t+0.04，另有两台同样型号的发动机作温贮备，贮备期的失效率为常数λ=0.0001，贮备的发动机进行工作的失效率为λ2(t)=0.004t+0.04，转换开关服从p=0.95的0-1分布，转换瞬时完成，设三个发动机工作寿命相关结构服从参数θ=-0.2的Frank Copula函数，尝试分析系统工作时间的可靠度。

根据部件工作寿命失效相关，开关服从0-1分布的温贮备系统可靠度计算模型（12），易得：

独立情形仅仅是相关性的一种特殊情况，若是假定X1，X2，X3是 独 立 关 系 ，则 只 需 将 Copula 函 数 取 为C(u1，u2，u3)=u1u2u3。则其系统可靠度R随时间t的变化，如图1所示。

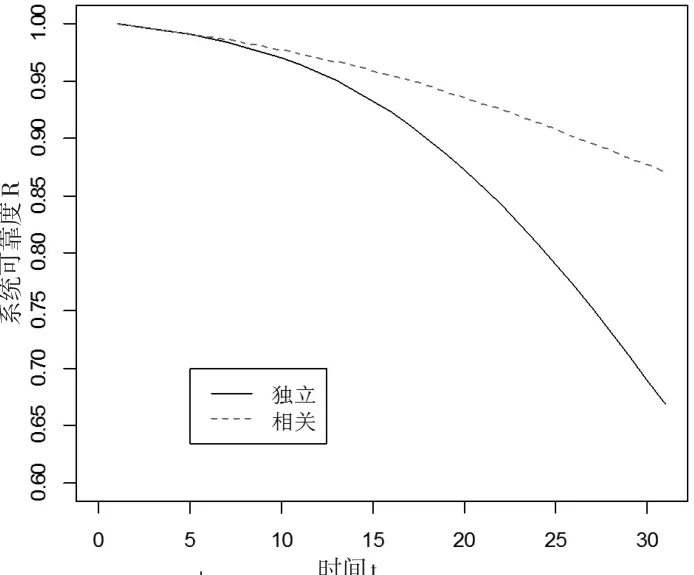
图1 发动机系统可靠度变化对比图

从图1可以得出，系统的可靠度随工作时间的增加而降低。考虑零部件失效相关和相互独立，分别计算系统的可靠度，其差异随工作时间的增加而增加，当工作时间较大时，差异较明显。

7 结论

部件失效相关性是机械系统可靠性工程的一个重要特征。为此，本文基于Copula相关性理论，考虑了转换开关的分布类型，在零部件失效相关性下，建立了n部件冷贮备系统和温贮备系统可靠度的普适模型，算例发现：在零部件失效相关和独立下，两者可靠度差异较为明显。按照传统独立模型获得的可靠度结果往往过于保守，易造成对系统可靠性的错误估计。

虽然相关性贮备系统可靠性计算模型稍显复杂，但是n部件冷贮备系统和温贮备系统可靠度普适模型的计算规律可以通过计算机程序实现。当然相关结构Copula函数的确定以及其中相关程度参数的估计需要以样本数据为前提，借助相关统计理论方法完成。

在本文建立模型的基础上，下一步可以在某种约束下，比如在费用、技术等约束条件下，探讨系统的冗余贮备最优分配方案等更多可靠性工程应用策略。