基于共因失效的海水系统多状态可靠性分析

黄泰俊，杨自春，陈国兵，费志方

(海军工程大学动力工程学院，湖北武汉 430033)

船舶动力系统是一个复杂度高、可靠性要求高的系统。动力系统部分设备及子系统存在冗余，且由于不同航行工况对系统性能输出的要求不同。系统中的设备处于不同的内部工作环境，导致相同设备存在不同的失效率，而多个设备存在于相同的外部环境之中，导致系统存在共因失效。由于进行动力系统可靠性分析需要考虑的因素众多，从而成为此类问题分析的难点。因此对这类系统进行可靠性分析，可以对系统的设计和维修决策提出有效建议，具有实际工程意义。

动力系统由多个分系统构成，包含各种串并联系统以及k/n(G)系统。由于船舶运行工况复杂，使动力系统存在多种工作状态，传统的二态可靠性分析方法因为忽略系统中间状态，导致分析结果过于保守，不能准确的评估系统的可靠性，因此，本文采用多状态分析方法对动力系统进行可靠性分析。目前，对于多状态系统的研究方法主要有以下5种:布尔模型扩展法、随机过程 (主要是Markov过程)法、通用生成函数 (Universal Generating Function，UGF)法、随机仿真 (主要是Monte Carlo仿真)法以及贝叶斯网络法等。其中，由于通用生成函数在处理复杂的多状态系统可靠性方面，具有计算复杂程度小、处理离散随机变量组合简洁高效等优点，被广泛运用［1－4］。以上研究均是在只考虑系统设备独立失效的情况下进行的。

然而，由于工作环境的影响，使动力系统设备之间存在共因失效。共因失效是增加失效概率的主要原因之一，会降低冗余单元提升系统可靠性的效果。针对这个问题，国内外学者把共因失效作为系统可靠性的一个重点因素进行了相关研究［5－7］。

以上研究考虑的都是相同单元在相同失效率和修复率情况下的可靠性分析问题，而动力系统中存在由于工作环境不同导致的相同单元失效率不同的情况，针对此问题以及动力系统存在多状态和共因失效等问题，本文利用通用生成函数，结合根据非同型单元可靠性分析［8］改进的Markov过程，提出相同单元存在不同失效率且考虑完全共因失效情况的k/n(G)系统的可靠性分析方法，并以海水系统为例，对其进行可靠性分析。

1 多状态系统的状态定义

假设系统由n个单元组成，其中单元j(j=1，2，…，n)有kj个状态，其中包括了正常状态1、失效状态kj以及中间状态 (2，…，kj－1)，则单元状态性能向量表示为gj= {gj1，gj2，…，gjkj}和对应的状态概率为pj(t) = {pj1(t)，pj2(t)，…，pjkj(t)}。单元的输出性能被看做为一个离散状态连续时间的随机过程Gj(t)，有Gj(t)∈gj，单元状态概率和输出性能值间的关系为pjhj(t) =Pr{Gj(t) =gjhj}(hj=1，2，…，kj)。

对于系统而言，系统输出性能由全部n个单元的性能状态决定，假设系统存在K个性能值，则单元和系统之间存在如下映射关系:

2 通用生成函数法

2.1 通用生成函数的运用

利用UGF进行系统可靠性分析时，通过引入z变换函数，首先要对系统及系统单元进行状态和性能描述。UGF定义了随机变量的可能取值与其对应的概率之间的联系，并通过运算建立了不同变量之间的关系。定义t时刻单元j的UGF为［9］:

定义UGF的运算法则，引入算子Ωf，得到多状态系统 (Multi－state System，MSS)的UGF为:

式中:U1(z，t)，…，Un(z，t) 为各单元的UGF。

根据串并联的结构特点，定义系统结构函数f(·)的计算法则:

1)对于串联系统，系统输出性能取决于性能最弱的单元，定义运算符δ1:

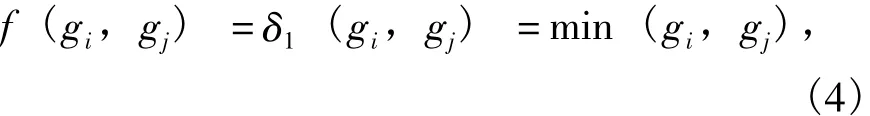
式中:gi、gj表示2个不同单元的性能值。

2)对于并联系统，若系统性能由各单元一起分担，定义运算符δ2:

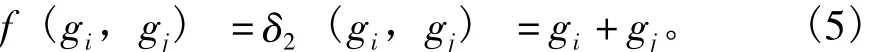
3)对于并联系统，若系统性能取决于性能最强的单元承担，定义运算符δ3:

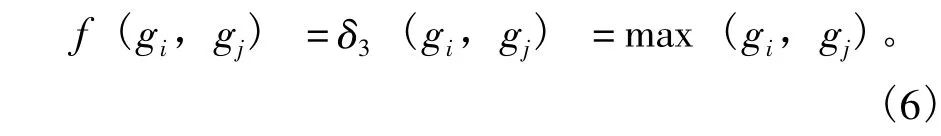
2.2 通用生成函数评估指标

由于UGF表示多状态系统的瞬时性能分布，因此可以用于评估瞬态可用度、平均瞬态性能等。

使用算子δA可得到在任意t(t＞0)时刻实际性能需求值为w时的系统瞬态可用度［9］:

使用算子δE可得到在任意t(t＞0)时刻系统的平均瞬态性能为:

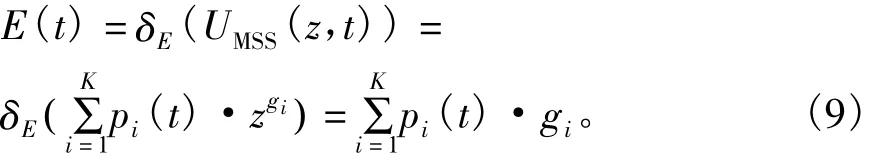
3 基于共因失效的可靠性分析改进方法

由上节所知，利用通用生成函数方法进行多状态系统可靠性分析，关键在于确定状态的性能值和对应状态的概率，对于单元j而言，即计算式 (1)中的gjhj和pjhj(t)，对于整个系统而言，即计算式(7)中的gi和pi(t)。其中单元性能值由单元本身决定，系统性能值由组成系统的单元之间的结构关系决定。

本节将利用Markov过程进行系统状态的概率分析。对存在共因失效单元的k/n(G)系统作以下假设。

1)系统中单元的寿命和维修时间均服从指数分布，且单元只存在工作和失效2种状态。

2)系统由n个失效率不同的相同单元组成，其对应失效率分别为 (λ1，λ2，…，λn)，至少有k(k=1，2，…，n)个单元正常工作时，系统正常;否则，系统失效。

3)系统进入故障状态时，其余正常单元停止工作。

4)单元可修，且有足够的维修工，各单元的维修率相同为μ。

5)共因失效发生时系统失效，共因失效率为λ*。

对k/n(G)系统存在状态进行定义。从失效单元个数定义，状态有n－k+2个，失效单元数分别为0，1，…，n－k，n－k+1，n个。然而，由于每个单元失效率不同，所以在i(i=1，2，…，n－k+1)个单元失效的情况下又分为Cin个子状态。用0和1表示各个单元的工作状态，0表示失效，1表示工作。例如 t时刻的 (0，0，1，1，…，1)表示单元1和2失效，其他正常工作。若用EiSi表示系统所有状态，其中 Si=1，2，…，Cin，则t时刻的状态为E21(t)，用FiSi(t)表示状态EiSi(t)失效单元的位置，则F21(t) ={1，2}。令失效单元数n－k=r，以系统的单元失效个数表示的系统状态关系图，不存在共因失效和存在共因失效的系统状态转移图如图1所示。

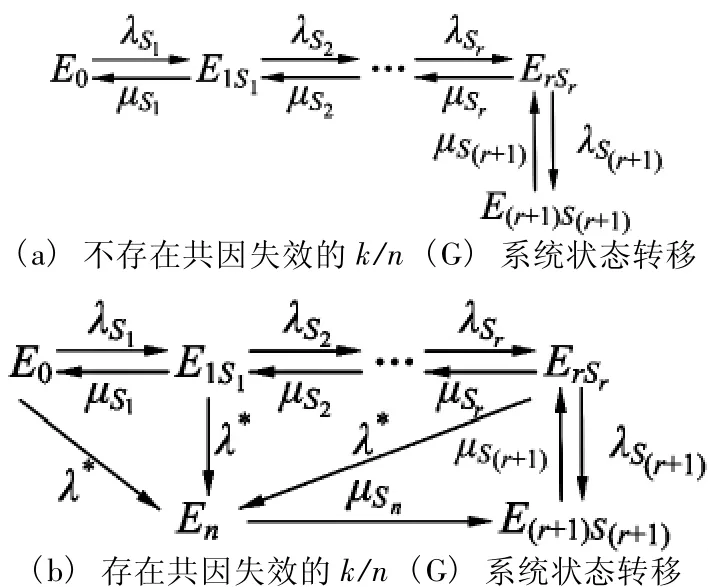
图1 系统状态转移

图1 中，λSi、μSi(i=1，2，…，r+1) 分别为失效单元数为i到失效单元数为i－1的状态的失效率及相反过程的修复率，μSn为单元全部失效到失效单元数为r+1时的修复率。

通过马尔科夫过程可以得到微分方程组(10)。

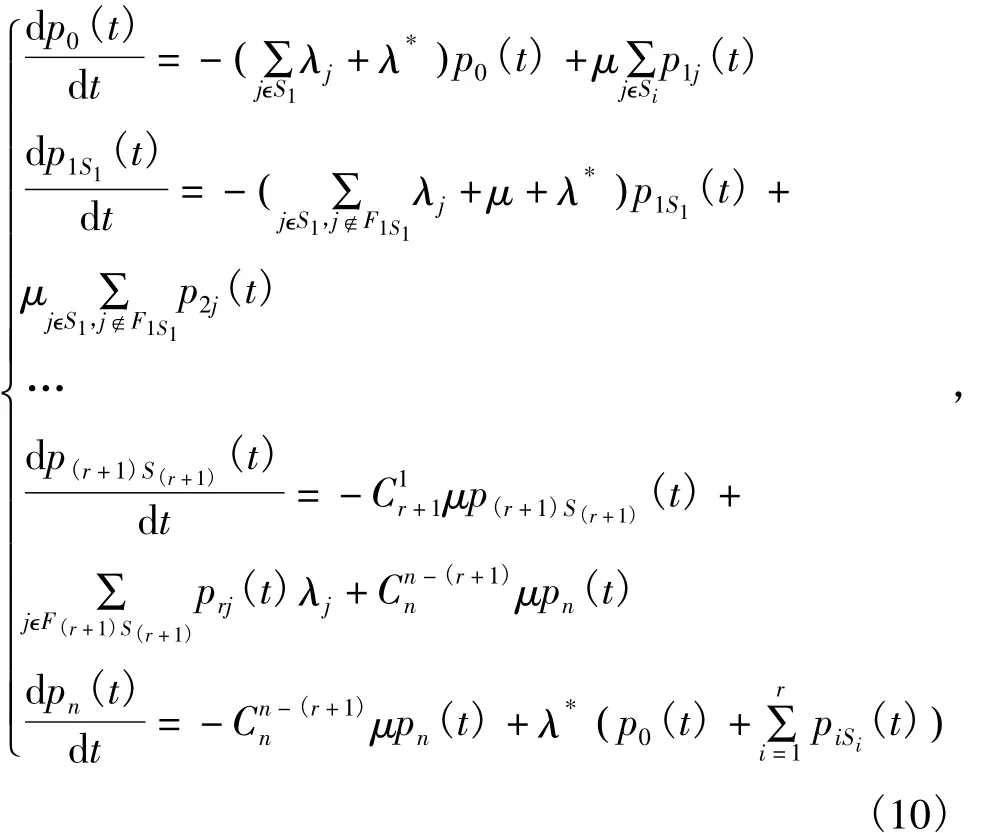
式中:pi(t)(i=0，1，…，r+1，n)为失效单元数为i时的状态概率，piSi(t)为失效单元数为i时子状态Si的概率，λj(j=1，2，…，n)为第j种单元的失效率。

本文使用MATLAB进行迭代运算，初始条件为p(t) = ［1，0，…，0］，即 p0(0) =1，pisi(0) =0，求解得到各状态的瞬态概率pi(t)。

对于不需要了解瞬态概率，只关心稳态可靠性能的系统，可以把各状态概率pi(t)作为常量，带入式 (10)进行计算，对于微分方程组的求解，也就转换为求解线性代数方程，可以得到多状态系统的稳态概率值pi(∞)。

4 算例分析

4.1 算例1

以文献 ［7］的算例3为研究对象，由于该系统的单元失效率相同，所以把λ1=λ2=0.001/h、λ*=0.000 5/h、μ =0.004/h代入式 (10) 得到结论，如表1所示。

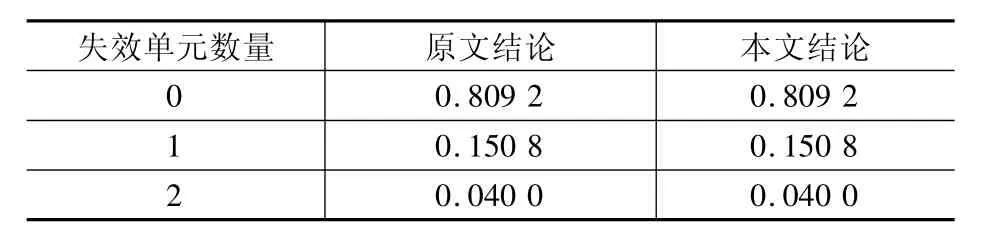
表1 结论对比

其中，在本文结论中失效单元数为1时的概率计算为:

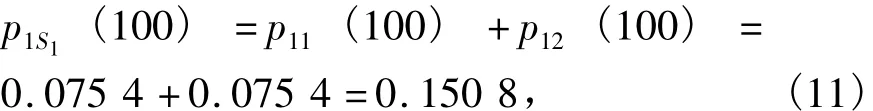
所以本文结论与文献 ［7］一致，验证了本文所提出方法的正确性。

4.2 算例2

4.2.1 海水系统的多状态模型

海水系统的用途是向动力设备和用水用户提供足够的冷却海水保证它们的正常工作。本文以海水系统为例，建立多状态系统的计算模型，如图2所示。其中，1、2、3、4、5分别代表5台海水泵，1、2为共因失效组1(CCG1)，3、4为共因失效组2(CCG2)，5号泵为轴系海水泵，其与前两组海水泵互为备用。

由于泵1、2、泵3、4以及泵5分别在3个不同舱室之中，且由于2号海水泵在储备状态时连接普通电源，工作时连接可靠电源，4号海水泵连接可靠电源，其余海水泵连接普通电源，导致各泵的独立失效率不同;由于泵的型号相同，所以各泵的修复率相同。设λi为各泵的独立失效率，μ为修复率。不同舱室的整体工作环境不同，所以不同舱室海水泵的共因失效率也不相同，、分别为共因失效组1、2的共因失效率。根据设计值，相应数据如表2所示。

图2 海水系统结构

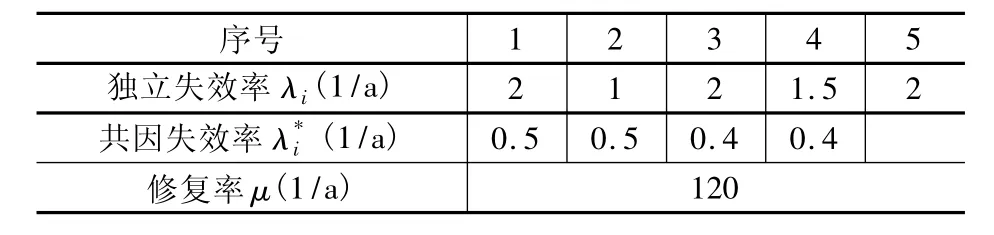
表2 可靠性参数

4.2.2 海水系统可靠性分析

1)稳态分析。由于每个海水泵只存在工作和失效2种状态，海水泵的额定流量为250 t/h，所以gi={250，0}。对于共因失效组1而言，把表2中数据带入式 (10)，再联合式 (3)、(5)，得到共因失效组1(子系统1)的稳态通用生成函数为:

同理，得到共因失效组2(子系统2)的稳态通用生成函数函数为:

单元5(子系统3)的稳态通用生成函数函数为:

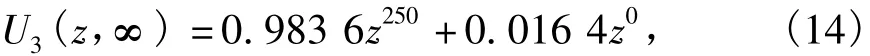
最后得到海水系统的稳态通用生成函数为:

根据式 (9)得到海水系统的平均稳态性能为:

在船舶的不同航行工况下，对于海水系统的供水量要求不同:

(1)在工况1下，w=964.8 t/h，则 A(∞，w)=0.994 0;

(2)在工况2下，w=814.8 t/h，则 A(∞，w)=0.994 0;

(3)在工况3下，w=364.8 t/h，则 A(∞，w)=0.999 9;

(4)在工况4下，w=267.8 t/h，则 A(∞，w)=0.999 9。

2)瞬态分析。精确值的解法为，结合初始条件对式 (10)进行Laplace－Stieltjes变换，再进行Laplace－Stieltjes反变换可以解得各状态的瞬态概率表达式，即piSi(t)。结合式 (3)、(5)得到海水系统瞬态通用生成函数表达式UMSS(z，t)。

本文结合稳态概率计算过程的数据，利用Origin生成相应图形。以1 000＜w＜1 250为例，则:

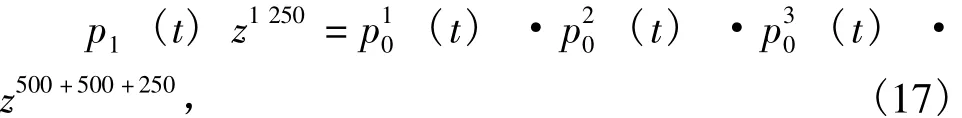
根据上式可以得到系统单元独立失效和考虑共因失效时的瞬态可用度A(t，w)和平均瞬态性能E(t)，如图3、图4所示。

图3 海水系统变工况下瞬态可用度对比

图3 中，NO CCF1和CCF1分别代表单元独立失效和共因失效时，系统性能输出要求为500＜w＜750时的可靠性水平;NO CCF2和CCF2分别代表单元独立失效和共因失效时，系统性能输出要求为750＜w＜1 000时的可靠性水平;NOCCF3和CCF3分别代表单元独立失效和共因失效时，系统性能输出要求为1 000＜w＜1 250时的可靠性水平。

根据图3和4可知:①若不考虑共因失效，将会导致系统可靠性分析结果比实际情况偏高;②海水系统的可靠性指标在系统开始运行后，迅速收敛，根据瞬态指标的变化规律，可以在性能要求变化时，确定系统的检修周期;③系统冗余度越高，可靠性越高，但是随着冗余度的增加，对于系统可靠性的提升效果逐渐减小，可以根据此规律确定系统最合适的备件数量;④考虑共因失效时，系统的平均瞬态性能稳定值约为1 229 t/h，远大于最高需求性能964.8 t/h，说明海水系统有很高的可用度。

图4 海水系统平均瞬态性能对比

5 结束语

本文结合通用生成函数和Markov过程，对含有共因失效的多状态系统进行可靠性分析，基于已有的非同型单元k/n(G)马尔科夫系统可靠性分析方法改进提出了一种新方法，用于相同单元具有不同失效率并且存在共因失效的情况。并且用实例进行了验证，保证方法的正确性。通过研究有以下结论。

1)本文结合通用生成函数与Markov过程的多状态可靠性分析方法，解决了二态可靠性分析结果偏保守的问题，提高了可靠性分析的精确度。

2)共因失效将导致系统可靠性水平下降，本文研究结果也证明了对系统进行共因失效分析的必要性。

3)考虑共因失效改进Markov方法，克服传统可靠性研究只考虑独立失效和只考虑单元失效率相同的局限性，使本文的状态概率计算方法能够应用于存在共因失效的相同单元不同失效率的k/n(G)系统之中，同时由算例1的结果可以证明，此方法也可以运用于相同单元具有相同失效率的k/n(G)系统之中，具有一定的通用性。

本文考虑了单元寿命和维修时间都服从指数分布的情况，然而在机械设备当中，还存在非指数分布的情况。下一步工作将考虑单元寿命和维修时间服从非指数分布的情况。