摆石子儿的学问
2018-12-21
一天,孙悟空来到古希腊的毕达哥拉斯家,只见他正在地上摆弄小石子儿呢。孙悟空走上前问:“大数学家毕达哥拉斯,你怎么像小孩一样玩起小石子儿来了呢?”
毕达哥拉斯对孙悟空说:“这摆石子儿的学问可大呢!大圣,你来看,我摆的是三角形数。”
孙悟空问:“这有什么学问?”毕达哥拉斯指着小石子儿说:“你把任意相邻的两堆石子儿数相加,看看结果怎样?”
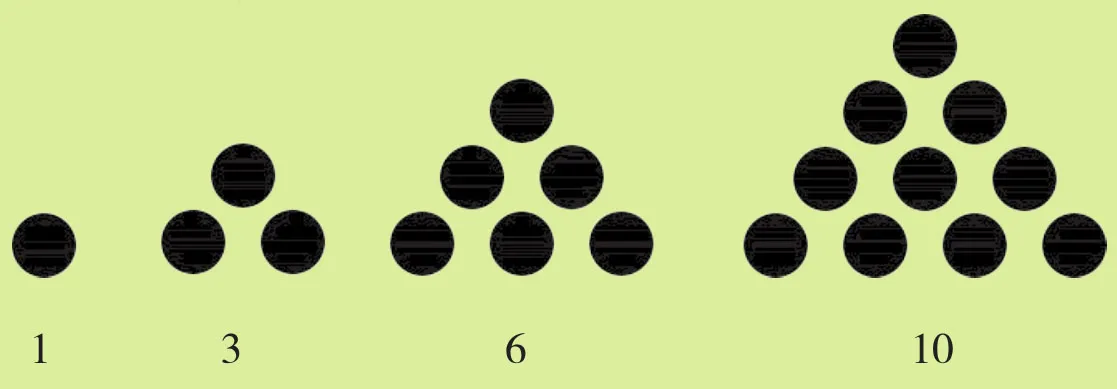
孙悟空听了后算了算:1+3=4=22;3+6=9=32;6+10=16=42。
孙悟空算完后笑了:“嘿,真好玩!它们相加正好等于一个自然数的平方。”
毕达哥拉斯对孙悟空说:“我把这些数叫作三角形数。大圣,你知道第1000个三角形数是多少吗?”孙悟空想了想对毕达哥拉斯说:“不知道,请你告诉我。”
毕达哥拉斯对孙悟空说:“大圣,你看!我取一个点,就得到第1个三角形数。

再添两个点,得到第2个三角形数。

然后又添上三个点,就得到第3个三角形数。

讲到这里,孙悟空说:“对了,这样可以得出一个规律:第几个三角形数就是前几个自然数的和。从中看出第10个三角形就是前10个自然数的各数之和,就是求1+2+3+…+10=?”
“怎样求出前10个自然数的和呢?一个数一个数地加太麻烦了。”孙悟空挠着后脑勺儿说。
毕达哥拉斯说:“可把另一个完全一样的三角形倒过来与原三角形拼成一个平行四边形,如下图:
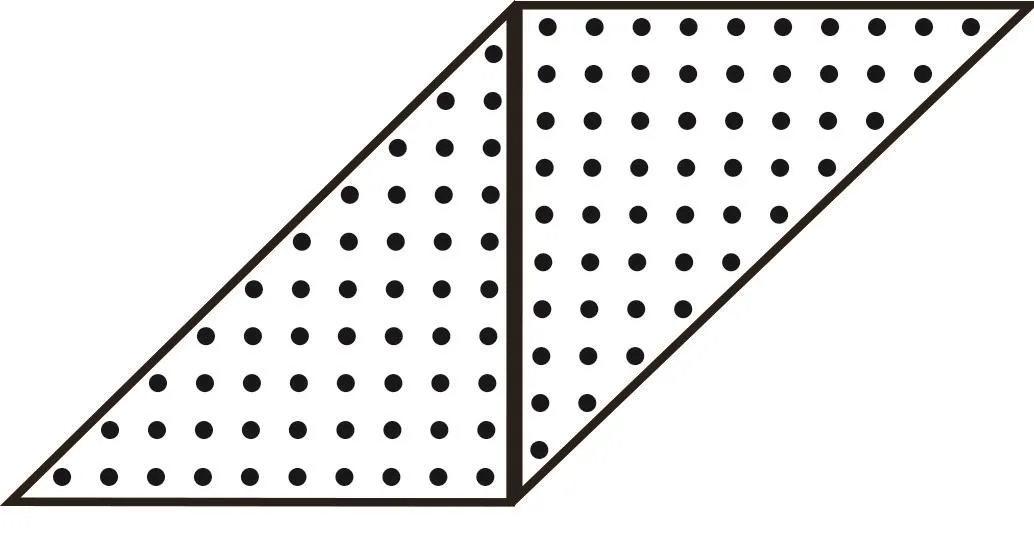
这个平行四边形一共有10行,每行都有11(1+10)个点,共11×10=110个点,每个三角形就有110÷2=55个点,所以第10个三角形数是:1+2+3+…+10=(1+10)×10÷2=55。
毕达哥拉斯讲完,对孙悟空说:“大圣,现在你知道第1000个三角形数是多少吗?”
孙悟空拾起一根树枝,在地上画了起来:1+2+3+…+1000=(1+1000)×1000÷2=1001×500=500500。孙悟空做数学的兴趣来了,对毕达哥拉斯说:“你的做法相当于把两个相同的和式‘倒序相加’,如:
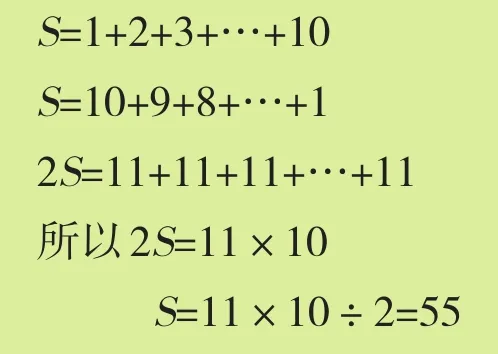
大数学家,在2500多年以前你能用这种方法巧妙地求出若干连续自然数的和,实在是很了不起。”
