逆向思维的假设解题

张海燕 符云锦

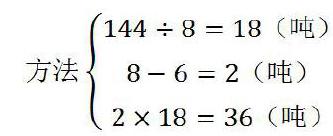
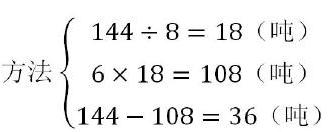
摘要：小学应用题解题能力是锻炼学生的学识水平，解析小学应用题的思维是关键，用逆向思维方法解题是深入挖掘学生大脑，能更好地培养和提升学生数学水平的综合能力。

关键词：应用题；逆向思维；解题

小学应用题的解题能力是小学阶段必须掌握的数学能力，也是新课标的重要内容及要求。因而解析应用题的思维能力是培养小学生必不可少的一项教学内容。在解应用题时，教师必须要注重学生的分析能力的培养，特别是应用题的正常分析能力，要善于引导学生进行正确分析理解题意，从而获得解题的思路和方法。

一般来说，我们按照正常的思路来分析的话，首先应从应用题所描述的事情来分析，要弄清事件的来龙去脉，搞清楚时间得发展过程；然后从题意中找到已知量及量之间的关系，还要找到题意中所要求的是什么或者是怎样的判断；最后根据分子得出来的量及量之间的关系進行列式计算，从而获得解答。

按照正常的思路进行解题，是每名学生必须掌握的应用题解题方法，是教师必备课。但是，有时按照正常思路解题，目的却不是很清楚，分析到完都不知道题目所求上网量或者判断与已知条件是怎样的直接关系，因此就需要逆向思维进行分析。首先，要从题目所求的量或者判断入手，找到需要的量或者需要的两个判断的量；然后，根据这些需要的量，再去寻找与他们有着直接或间接的相关量，当然这些相关量可以是题目已经给出的，也可以是从题目中求出的；最后，在反序一下，就可以得出题目的解法。

用逆向思维方法解题是深入挖掘学生大脑、激发思维的重要手段，同时也是考验学生对所学知识的掌握情况，对所学知识的迁移能力，对日常生活中的应用分析能力，更大地锻炼学生的综合应用能力。下面举个例子来分析。

某沙场有甲、乙两堆沙子各144吨，甲堆沙子每天运走8吨，乙堆沙子每天运走6吨。问当甲堆沙子运完时，乙堆沙子还剩多少吨？

按照正常的思路来分析，甲堆沙子每天运走8吨，我们可以算出：144÷8=18（天），可知甲堆沙子运完需要18天，这是乙堆沙子运走的吨数为：6×18=108（吨），乙堆沙子还剩36吨没有运走，这种解法列式为：

按照逆向思维来分析，当甲堆沙子运完时，乙堆沙子还剩多少吨？于是，我们就必须知道，乙堆沙子已经运走了多少吨。从题意中可以得出，乙堆沙子每天运走6吨，那么我们只需知道乙堆沙子运了多少天即可，这时我们想到，甲堆沙子刚好运完，再从题意又知甲、乙两堆沙子运走的时间天数是相同的，所以只要把甲堆沙子运完所花的时间算出来，问题就得解。而甲堆沙子每天运走8吨，共是144吨，不难算出甲堆沙子运完所花的时间。我们反序下，可以得出与方法①同样的列式计算。

此外，我们还可以得出方法②的列式计算：

方法②解释为：甲堆沙子运完需要18天，乙堆沙子运完需要24天，乙堆沙子运完要比甲堆沙子多运6天，而乙堆沙子每天运6吨，当甲堆沙子运完时，乙堆沙子运完还需要6天，所以剩下的沙子就是剩下6天所要运的沙子。

在课堂上，学生除了用方法①、②外，还出现了第三种方法，列式计算为：

该学生又不能解释方法③的解义，解释不通计算的结果，但方法③确实是正确的。那么方法③应该怎样理解呢？

我们知道，方法③的第一步和第二步与方法①、②一样好理解，先是算出甲堆沙子运完时需要18天，甲堆沙子每天比乙堆沙子多运走2吨，关键是第三步算式不好理解。第三步从算式上理解为在甲堆沙子运完时，甲堆沙子比乙堆沙子多运多少吨？如果算式有实际意义的话，那么第三步算式应理解为当甲堆沙子运完时，甲堆沙子比乙堆沙子多运的吨数和一堆沙子剩下的吨数相等，问题的关键就在这里，是否真的相等尚待理解，从字意来理解确实理解不同。

我们再想想，甲、乙两堆沙子的重量是相等的，所以回答是肯定的。我们换种思路来思考：反过来，如果乙堆沙子每天运走8吨沙子的话，那么当甲堆沙子运完时，乙堆沙子应该也会全部运完，而实际上乙沙子每天是少运了2吨，也就是说，乙堆沙子每天剩下2吨没有运走，所以，当甲堆沙子运完时，乙堆沙子少运了2×18=36吨，这刚好就是乙堆沙子剩下没有运走的沙子！这种理解符合实际，也容易理解。因此，方法③也是正确的。

综上所述，方法③是换种思考方式来分析，我们把“甲堆沙子比乙堆沙子每天多运2吨”进行逆向思维假设成“如果乙堆沙子每天也能运走8吨下，而实际上乙堆沙子每天只能运走6吨，剩下2吨沙子没有运走”，导致了“当甲堆沙子运完时的18天内，乙堆沙子就剩下了36吨沙子没有运完”，方法③得以理解。为此，在解答小学应用题时，学生不妨把已知条件逆向假设一下，也许很难理解的解题思路就变得容易理解了。

参考文献：

[1]义务教育课程标准实验教科书.四年级数学上册[M].北京：人民教育出版社，2017