抑制钻柱黏滑振动和钻头反弹的建模与控制

2018-12-20张奇志吴永强

石油钻采工艺 2018年5期

张奇志吴永强

1.西安石油大学电子工程学院；2.陕西省油气井测控技术重点实验室

钻柱黏滑振动是由强烈的横向振动和地下摩擦阻力引起的一种极具破坏性的扭转振动现象，而钻头反弹是由钻头与岩层之间轴向运动产生的一种轴向振动现象。近年来，为了抑制钻柱黏滑振动，国内外专家学者对该问题进行了大量研究，其研究的主要内容可概括为3个方面：（1）通过对钻柱旋转系统、起升系统的简化，建立钻柱黏滑振动的动力学模型，分析钻头类型、钻井参数及负载特性对黏滑振动的影响，并进一步对黏滑振动的成因和规律进行分析和总结［1-2］；（2）通过钻井勘探现场和室内实验对钻柱黏滑振动的成因、特点及其控制策略进行分析研究，例如刘曙光等提出柔性扭矩控制方法来消除钻柱黏滑振动现象［3-4］；（3）采用 Abaqus、ANSYS 和Patran/Nastran等有限元分析模拟仿真软件建立钻柱系统黏滑振动和钻头击破岩层的有限元模型，研究钻柱黏滑振动的特性及规律，进而对理论分析和试验结果进行验证［5］。

国内外专家学者的研究在很大程度上抑制了钻柱黏滑振动现象，然而在对钻柱黏滑振动进行控制的同时忽略了钻头反弹问题。笔者基于黏滑振动和钻头反弹的运动机理，建立了钻柱旋转系统和起升系统的动力学模型，设计了基于线性二次型（LQR）控制策略的钻柱旋转系统和起升系统的状态反馈控制器，用于抑制钻柱黏滑振动和钻头反弹现象。仿真结果表明，LQR控制器的引入使得钻头转速稳定在给定转速附近，减少了钻压和扭矩波动，抑制了黏滑振动与钻头反弹现象，钻柱运行更加平稳。

1 钻柱系统的动力学模型

在钻井过程中，由直流电机经变速箱传动带动转盘旋转，转盘通过方钻杆来带动井底钻具组合（Bottom hole assembly，简称 BHA），从而实现钻头旋转钻进击破岩石。其旋转系统的简化模型如图1所示。

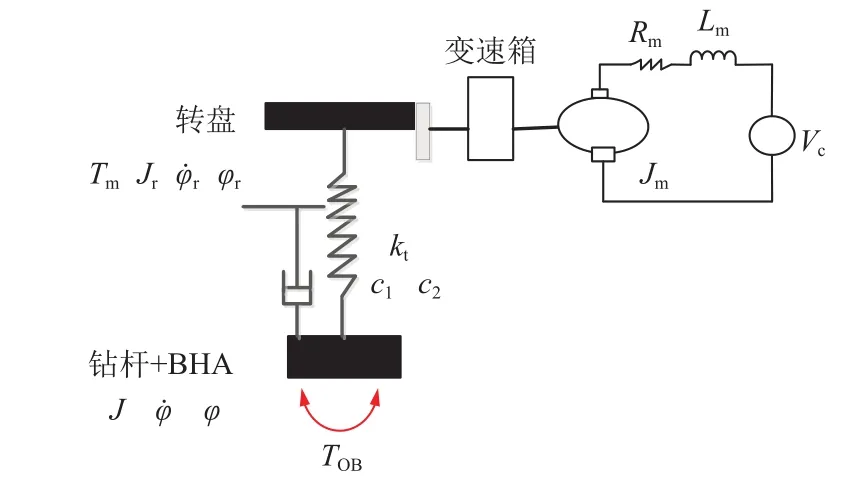
图1 钻柱旋转系统简化模型Fig. 1 Simplified model of rotation system of drill string

假设绞车给定快绳的拉力为F0，其经过游车和大钩带动钻杆及井下设备完成钻柱系统的起升功能，起升系统的简化模型如图2所示。

1.1 钻柱旋转系统数学模型

图2 钻柱起升系统简化模型Fig. 2 Simplified model of lifting system of drill string

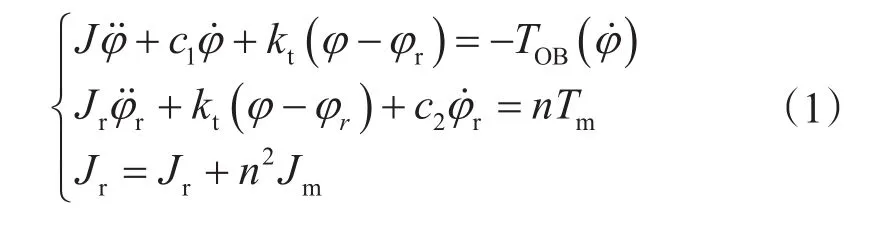
在图1中，钻柱旋转系统的运动方程可表示为钻柱旋转系统的驱动电机以他励直流电动机为例，其特性方程可表示为

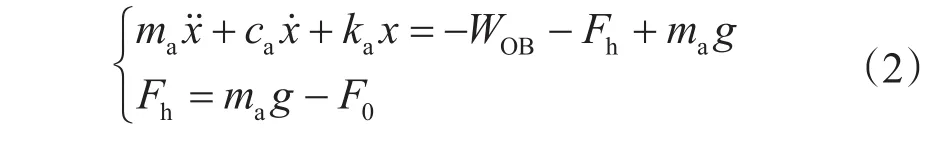
式中，φ、φr分别为钻头和转盘的角位移，rad；分别为钻头和转盘的角速度，rad/s；J、Jr、Jm分别为钻柱、转盘和电机的转动惯量，kg·m2；TOB（φ˙）为钻头扭矩，N·m；c1为钻柱与钻井液之间的阻尼系数，N·s/rad；c2为转盘阻尼系数，N·s/rad；kt为钻柱旋转方向的阻尼，N·m/rad；Tm为直流电动机驱动扭矩，N·m；I为直流电机的电流，A；Rm为直流电机的电枢电阻，Ω；Lm为直流电机的电枢电感，H；Vc、E分别为直流电机输入电压和反电动势，V；ωd为钻头给定角速度，rad/s；Km为电机常数，V/s；n为直流电动机与变速箱的齿轮比。

1.2 钻柱起升系统数学模型

在图2中，钻柱起升系统运动方程可表示为

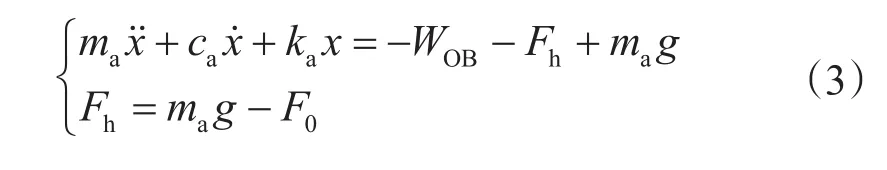
钻压WOB可表示为

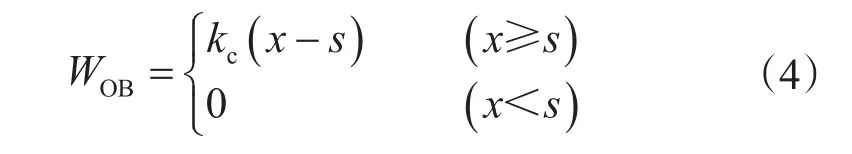
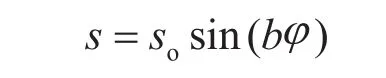
其中钻头的扭矩TOB与钻压WOB相关［6］，钻头扭矩可表示为

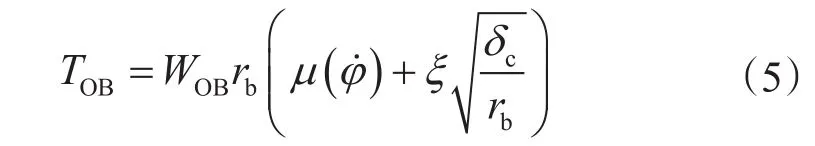
其中

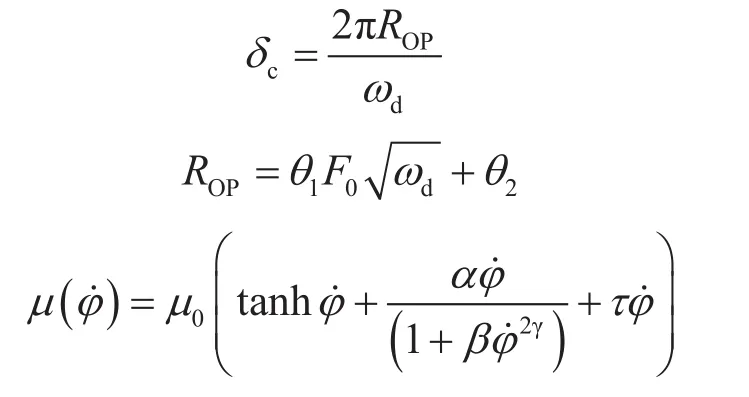
式中，ma为钻井设备总质量，kg；x为钻头轴向位移，m；Fh为大钩负载，N；kc为地层刚性系数，MN/m。

1.3 钻头负载特性模型

在双自由度钻柱旋转系统的模型中，旋转系统摩擦力矩可简单认为是钻头上的反力矩TOBr和BHA上的非线性摩擦力矩TOBf之和［6］。图3为钻头摩擦力矩与钻头角速度的关系图。

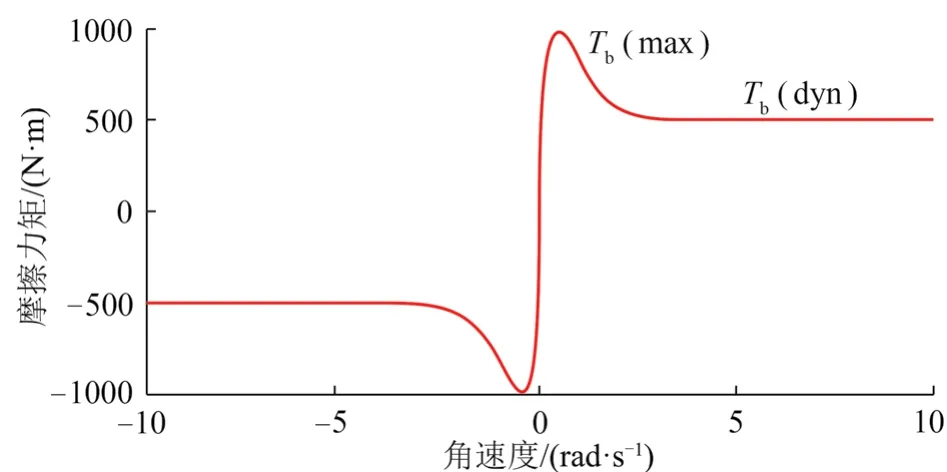
图3 摩擦力矩与钻头角速度的关系Fig. 3 Relationship between friction torque and bit angular velocity

2 控制器设计

为消除黏滑振动和钻头反弹问题，本文将分别设计线性二次性（LQR）控制的钻柱旋转系统和起升系统的状态反馈控制器［7-8］。

2.1 扭转状态反馈控制器

对方程（1）、（2）进行线性化处理得到钻柱旋转系统的平衡方程为

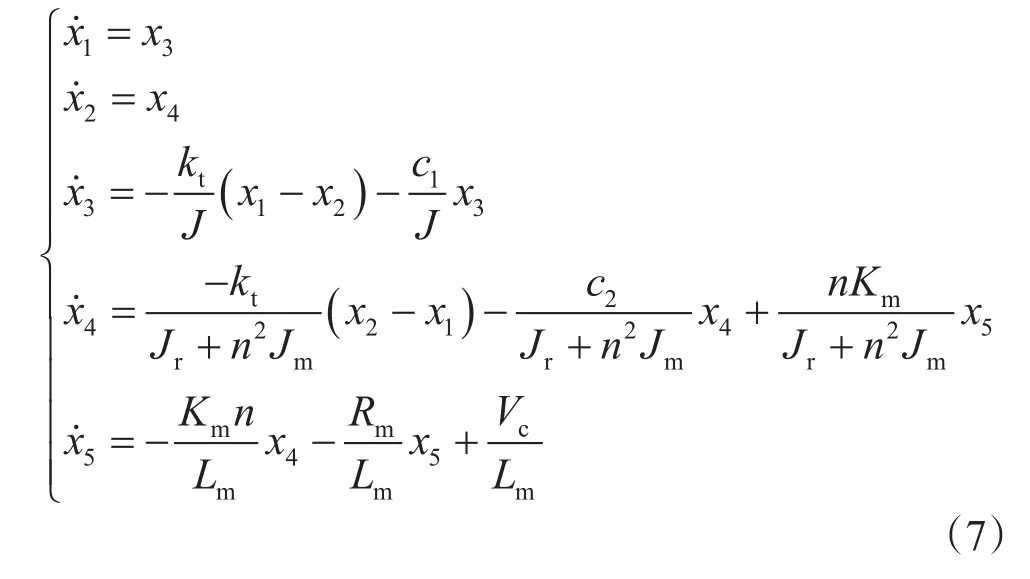
将式（7）写成状态空间形式为

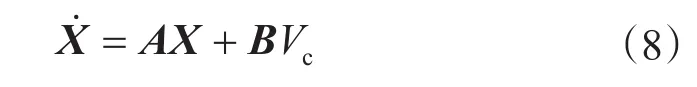
式（8）中的A为系数矩阵，B为输入矩阵，X为状态矢量，其分别表示为

在设计LQR控制器前，需设计一个能量函数Φ，最优控制轨迹应该使得能量函数最小［7-8］，一般选取能量函数为

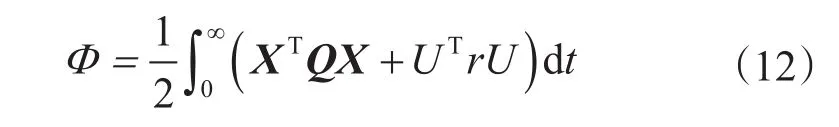
根据式（6）旋转系统的平衡方程可选取X为式（11）的5个状态向量，又因为本系统旋转方向的输入为转盘电机的供给电压Vc，且为一维向量，则UTrU可表示为rVc2。此外，要使能量函数Φ最小，则状态向量X和输入U都要小。Φ最小表明其为有界函数，随着时间t趋于无穷，状态向量X将趋于0，这也保证了闭环系统的稳定性。输入Vc小，则表示用最小的控制代价得到最优控制。式（12）中，Q是设计的半正定矩阵，r是正定矩阵。一般来说，如果Q值选得大，而要使Φ最小，则X需要更小，也就意味着闭环系统的矩阵（A–Bρ）的特征值处于S平面的左半平面，这样状态X就以更快的速度衰减到0。r与输入变量Vc有关，Vc的减小，意味着状态衰减将变慢。综合考虑这些因素，在设计扭转反馈控制器时，参数Q和r可分别选取为：因此，转盘电机的供给电压可表示为

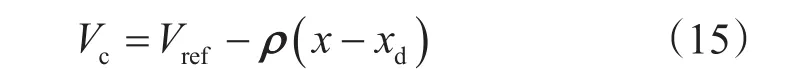
其中

P的求取可根据Riccati方程

在没有任何干扰的情况下，Vref是维持转盘转速给定电压。为了使钻柱振动得到控制，电机供给电压的扭转状态反馈控制器可以表示为

通过计算可得状态反馈控制增益ρ可表示为［15］

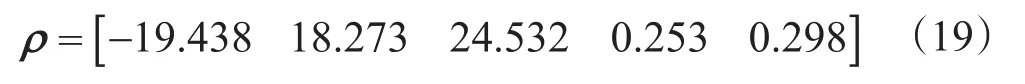
2.2 轴向状态反馈控制器

同理，在设计轴向反馈控制器之前，对方程（3）进行线性化处理得钻柱起升系统方程

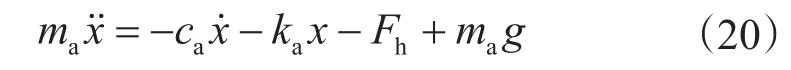
令ω=x，ω2=为状态变量得

将式（21）写成向量矩阵形式为

式中，X1为状态矢量，A1为系数矩阵，B1为输入矩阵。

为了使钻柱钻头反弹得到控制，同样可根据LQR控制策略，将大钩负载的轴向状态反馈控制器表示为

通过计算得轴向状态反馈控制增益ρ可表示为

3 结果与分析

表1是钻柱系统模型的钻井参数［9］。Matlab/Simulink仿真平台建立的钻柱系统模型见图4。

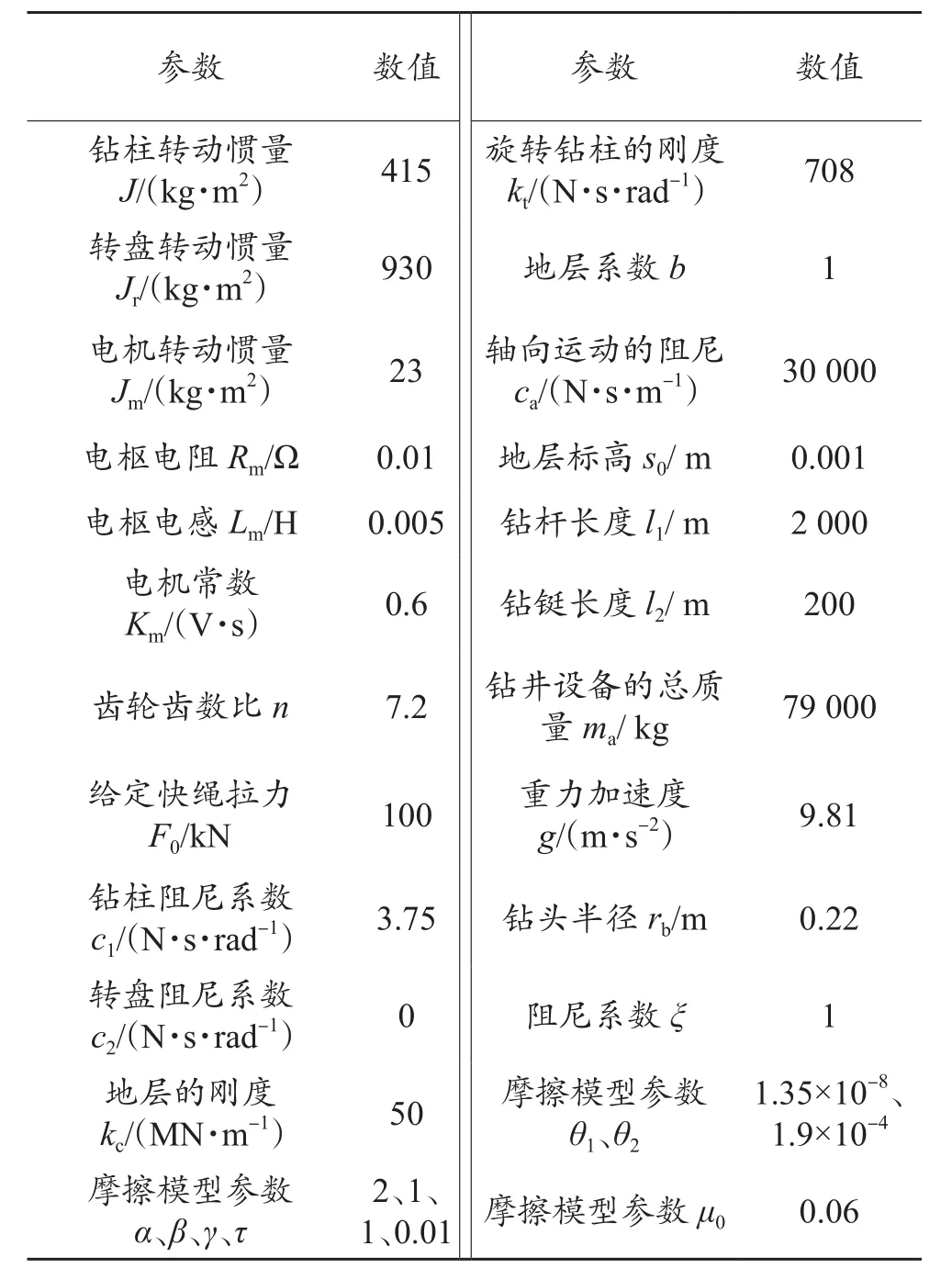
表1 钻井相关参数Table 1 Related drilling parameters

图4 钻井系统仿真模型Fig. 4 Simulation models of drilling systems

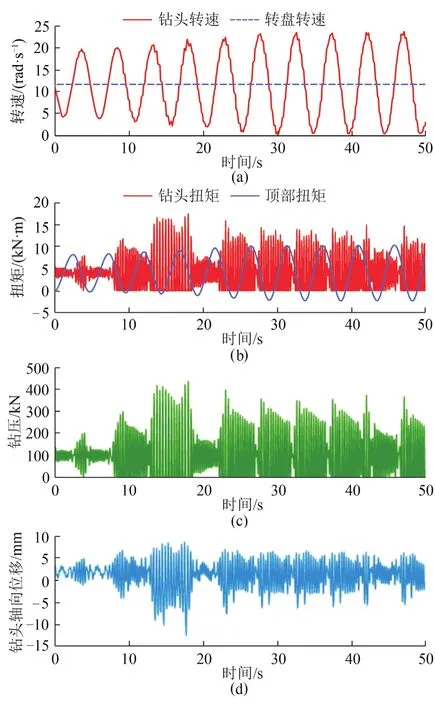
图5 钻头和转盘的转速、扭矩、钻压以及钻头轴向位移响应曲线（kc=50 MN/s，ωd =11.8 rad/s）Fig. 5 Response curve of drill bit with rotary speed, torque,WOB and bit axial displacement （kc=50 MN/s，ωd =11.8 rad/s）

钻井实践表明，增大转盘转速或减小钻压可一定程度减小黏滑振动现象，但同时产生了轴向振动和横向振动［10-12］，且黏滑振动抑制效果不明显。钻井现场调研发现，如果钻柱长时间处在黏滑振动和钻头反弹状态下，钻井设备就可能会严重损坏，最终导致钻井失败。为此，必须设计有效的控制器来抑制钻柱黏滑振动和钻头反弹现象。

首先，加入了扭转状态反馈控制器后，系统响应曲线如图6所示，在给定转盘转速ωd=11.8 rad/s 、地层刚性系数kc=50 MN/m时，当图6（a）中仿真时间达到25 s时钻头转速稳定在给定转盘转速11.8 rad/s附近，且起初钻头转速波动最高达20 rad/s。在图6（b）中钻柱扭矩起初有稍微波动，但10 s后最终稳定在5 kN·m附近，相比较图5（b）扭矩波动减少了66.7%，钻柱黏滑振动得到了很大程度抑制。图6（c）、（d）中，当给定钻压F0=100 kN、x0=2 mm时，钻压波动起初较大，最终稳定在80～120 kN之间，钻头径向位移波动起初也较大，最终稳定在0.8～3.5 mm之间，故钻头反弹现象减小不明显。

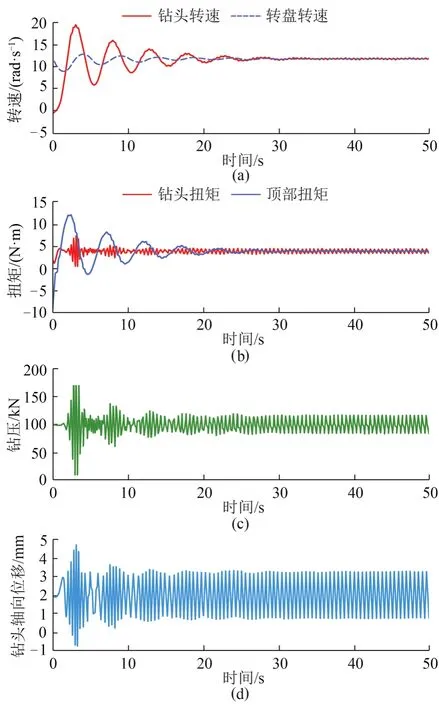
图6 仅加入扭转状态反馈控制器的钻井系统响应曲线（kc=50 MN/s，ωd =11.8 rad/s）Fig. 6 Response curve of drilling systems only with torsion state feedback controller （kc=50 MN/s，ωd =11.8 rad/s）

在给定参数不变的情况下，针对图6出现的问题同时加入扭转和轴向状态反馈控制器后，系统响应曲线如图7所示。当仿真时间达到25 s时，图7（a）、（b）中，钻头转速稳定在给定转盘转速11.8 rad/s附近，且钻柱启动3 s后扭矩就一直稳定在5 kN·m，同时消除了图6（b）钻头扭矩起初波动大的问题，故表明钻柱黏滑振动得到了抑制。图7（c）、（d）中，当给定钻压F0=100 kN、x0=2 mm时，钻压波动最终稳定在100 kN附近，钻头轴向位移波动在1.5～2.5 mm之间，钻头反弹现象也得到抑制。

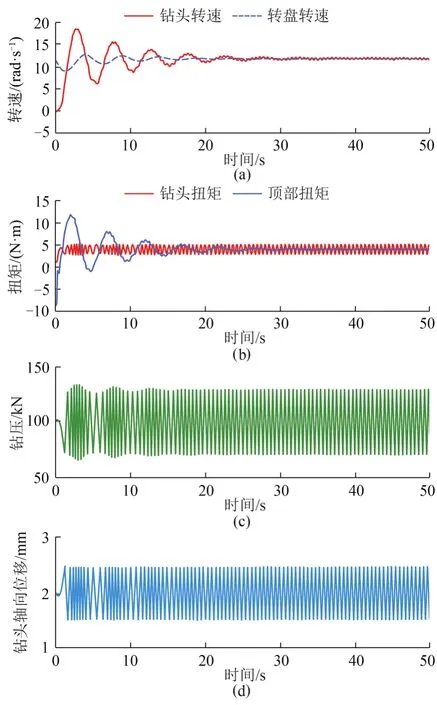
图7 同时加入扭转和轴向反馈控制器的钻柱系统响应曲线（kc=50 MN/m，ωd =11.8 rad/s）Fig. 7 Response curve of drill string systems with both torsion and axial feedback controllers （kc=50 MN/m, ωd =11.8 rad/s）