基于CNN-RSC组合优化算法语音情感分析与研究*

赵永生, 徐海青, 张引强

(1.安徽继远软件有限公司，安徽 合肥 230000;2.武汉大学，湖北 武汉 430000;3.国网安徽省电力有限公司信息通信分公司，安徽 合肥 230000)

国内外有很多针对文本进行情感分析方面的研究.研究者利用传统的机器学习算法，如支持向量机、条件随机场、信息熵等对文本进行情感分析.Pang等通过分别对朴素贝叶斯、最大熵和支持向量机三种模型进行训练，实现文本特征信息提取，并对比准确率[1].Turney分析文本中词语与正向和负向情感词的相关度，根据其相关度差值判断文本的极性，并对文本情感进行分类[2].Li等提出一种dependency-sentiment-LDA模型，该模型结合语境和局部依赖的关系分析文本情感，大大提高了情感分析的准确度，但此模型依赖人工标注数据集，降低了整体性能[3].Hinton等于2006年开始提出深度学习，由于深度学习技术能够对海量数据进行学习，因此其在文本情感分析中得以发展[4-5].Mnih等将一种可扩展的分层神经网络模型应用到了文本分析中，大大提高了训练速度和准确度[6].Mikolov等提出了一种基于循环深度神经网络的模型，并根据语料上下文信息进行模型构建，提高了容错率[7].上述方法往往忽视了语义的结构信息，而深度学习中的递归自编码模型，将文本中的语音信息融到在最佳树结构中，在特征信息提取、情感分析中具有优异的表现.

1 情感分析基础理论

本文中使用的卷积神经网络模型如图1所示.整个神经网络主要分为输入层、卷积层、池化层和全连接层.对于输入层，其输入基于样本句段的随机赋值生成或为语料预先训练好的词向量，如式(1)表示：

s=[w1,w2,w3,…,wn-1,wn] .

(1)

卷积层中包含通过窗口连接输入层的过滤器，获得输入样本中多个词之间的局部特征.若窗口大小为h，且作用在相同大小窗口的词向量上，可生成新的特征向量

ci=f(v·wi:i+h-1+b),

式中：b，v为卷积神经网络的参数.f(·)是关于v、w、b的非线性特征函数，利用函数变换得到新的特征向量c,c∈Rn-h+1.池化层的池化操作最终通过重构误差学习句段内各个词语直接的语序关系，降低句段的误差，生成最佳树结构，更好地表达句段原始语义.重构误差为

式中的n1、n2为当前节点c1、c2下面的词数.计算时，为了方便计算，我们对负节点进行归一化处理，

最终句段的情感分类是通过对所获得的最佳向量加入输出层进行的.输出层情感分类计算公式为：

d(p;θ)=soft max(wlabelp)，

式中：p为语句向量；soft max(·)为输出层的分类函数；wlabel为系数矩阵；label为情感的分类数.输出层误差为：

式中：d是一个概率的分布向量(维数为k，情感分类数等于k)，且dk=p(k|[c1;c2] )，∑k=1dk=1；tk为第k种情感标签值.对上述公式进行优化处理，优化目标函数选择为：

式中：N表示数据集的大小；E(x,t;θ)为某条语句误差；∑(x,t)E(x,t;θ)为整体数据集误差.因此若是要计算一整条语句的误差，即需要计算整棵树所有非终端节点的误差累加和：

E(x,t;θ)=∑s∈T(RAEθ(x))E([c1;c2]s,pst,θ) ，

式中：s为非终端的三元组表示；T()为遍历函数.如图2所示，在计算非终端的三元组误差时，通过同时考虑交叉熵误差和重构误差，提升预测结果精度.三元组s的误差为：

E([c1;c2]s,ps,t;θ)=αErec([c1;c2];θ)+(1-α)Ece(ps,t;θ) ，

通过参数α调整重构误差与交叉熵误差各自的权重.为了对公式进行优化，本文中采用L-BFGS算法快速求出最优解，其中，算法所使用的梯度为：

2 实验结果与分析

表1 实验结果分析Tab.1 Experimental results analysis

表2 封闭测试的实验结果Tab.2 Experimental results of closed test

按照输入样本词向量的类别来分，主要有随机初始化词向量、训练好且在训练过程中保持不变的词向量、训练过程中适当微调的词向量三类，对应着卷积神经网络CNN-rand、CNN-static、CNN-non-static三种调节模式，根据实验挑选适合的CNN调节模式.表1为在训练集上三种调节模式的交叉验证实验结果.

从表1中可以看出，CNN-non-static 模式相比其他两类调节模式的分类准确率最高，在后续的实验中，将统一使用 CNN-non-static 模式进行实验.

表2是对不同的神经网络参数下情感分类的对比，当Filter 参数设置为 [4,5,6] 、Hidden unit 参数设置为100时，情感分类准确率可达到0.846.递归自编码模型参数调节中，通过分别设置词向量的长度为10，20，…，130，重构误差系数为0.1，0.2，…，0.5，将二者的所有组合方式测试一遍，找出最优的组合，并统计在此数据状态下的算法准确度(准确度=预测正确条数/总条数)，结果如表3所示.

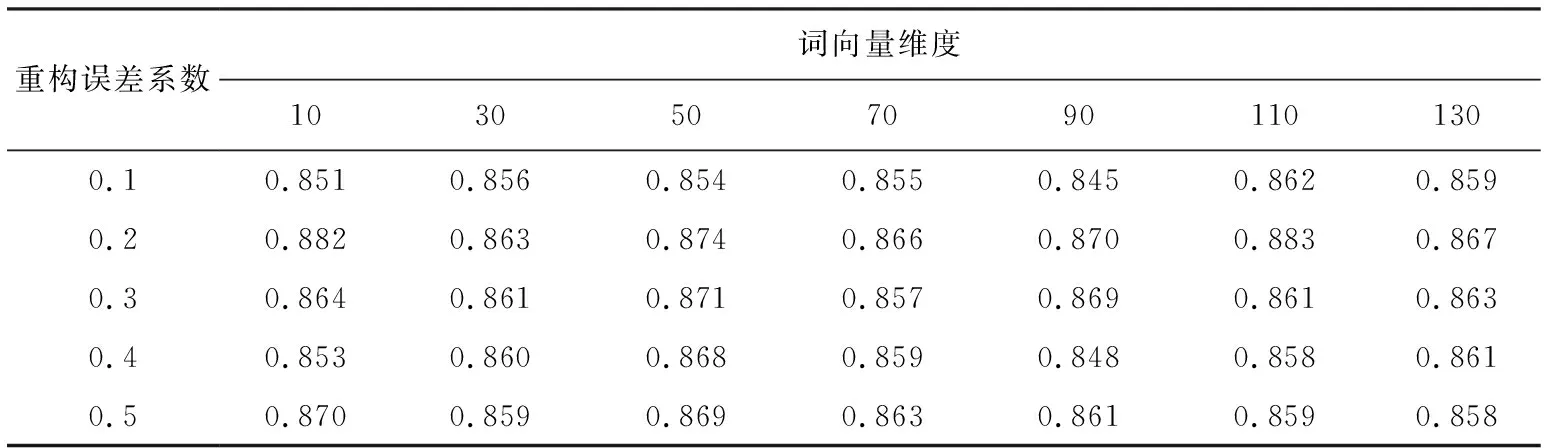
表3 算法准确度Tab.3 Algorithm accuracy

从表3 中实验结果可得出，当重构误差系数为0.2时，不同的向量维度，算法准确率都为当前维度下的最优值.特别地，当词向量维度为110时，算法准确率达到最大值0.883.将卷积神经网络参数和递归自编码参数都设置为当前组合，即Filter = [4,5,6]，Hidden unit =100；重构误差系数0.2，词向量维度为110.

通过不断增加数据量，从1万条语句逐渐增加到4万条，期望验证语料库大小与预测的情感倾向准确性的关系，同时通过改变中文语句量大小研究与模型训练时间的关联性.语料库大小与算法准确度的实验结果如图3所示.

表4 准确率、召回率和F1值的平均值Tab.4 Accuracy, recall and F1 values

由图3中可以看出，在中文语句量为1万条的时候，组合优化算法的准确度已经达到约85%.语句量达到4万条时，具有很高的准确度，算法准确度可达90%.之后再增加语句量，准确度的变化幅度不大.为了验证所提出的算法的准确性和有效性，使用单一的CNN和RSC情感分析算法作为对比，实验结果如表4所示，表4表示测试语料库中不同的算法所得到的文本情感分析的准确率、召回率和F1值的平均值.

由表4可见，对于不同的算法类别，本文算法CNN-RSC组合优化算法情感分析的准确度比其他两种算法模型高约15%，且递归自编码算法对文本分析的准确度要高于卷积神经网络算法.CNN-RSC模型的F1值比RSC高约12%，比CNN高约8%.

实验三种算法训练时间、准确度受语料库、迭代次数的影响，实验结果如图5所示.

从图5(a)和(b)中可以看出，三种算法模型训练时间廓形增长均逐渐加快.CNN-RSC算法模型，其训练时间从5 h左右增长到了30 h，扩大了6倍，说明当数据量过大时，深度学习训练很耗时，要想获得较好的算法效果，更需要较长的训练时间.由图5(c)可以看出，不同的算法其迭代次数与分类准确率关系具有相似的廓形.在最初的迭代过程中，随着迭代次数的增加，分类准确率都呈现不同程度的增加.然后，继续增加迭代次数，反而引起准确率的下降.当迭代次数增加到6次的时候，准确率基本不变，保持平稳.由图5(d)中可以看出，随着中文语句量的不断增加，三种模型算法的准确度廓形也呈递增的趋势.在语句量条数较少的时候,CNN-RSC准确率达到68%, 高于CNN和RSC.当语料库包含的语句从0.6万条扩张到4万条时，CNN和RSC算法的精度变化不大(最高约8.0%)，但是CNN-RSC算法的精度增加了约15.5%，说明使用组合优化深度学习算法其数据挖掘能力得到了提高，对语料库的学习能力增强.

3 结束语

本文首先系统地研究了目前国内外关于文本情感分析的各类方面，并针对传统的情感分析方法中存在的不足，提出了一种基于卷积神经网络和递归自编码模型的组合优化算法，该组合优化算法在文本情感分析的过程中，将预训练或者随机的词向量作为CNN的输入，CNN池化层的输出为样本的分布式特征，该分布式特征可作为递归自编码模型中的特征输入，进而对文本的情感进行分类.这样的模型有效地将CNN和递归自编码的优点结合在一起.在NLPCC-SCDL评测数据集上进行训练和测试，实验结果表明提出的组合优化算法在对文本情感特征的自动学习上有着不错的效果，模型的训练速度也大大地提高，在对文本情感问题的准确度和训练时间以及分类性能上均优于其他两种算法.