柯西不等式在初等数学物理中的若干应用

徐浩然

（安徽省合肥市第一中学高二（26）班，安徽 合肥）

法国著名数学家柯西，1789年8月21日出生于巴黎。他对数论、数学分析、抽象代数和微分方程等多个数学领域进行了深入的研究,并取得了许多重要成果。著名的柯西不等式就是其中之一。此不等式在初等数学的解题中应用上具有耳目一新、灵活巧妙的作用。有些参考书上采用了构造函数、利用判别式的方法来证明。而本文在此给出了三种更为简捷的证明法：引入了二次型法和数学归纳法，来证明柯西不等式。

定理 1 设 ai，bi为任意实数 i=1，2，…，n则，

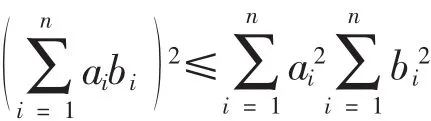
其中等号当且仅当ai，bi成比例时成立。（柯西不等式原命题）

1.证明方法

方法1（简洁证明）

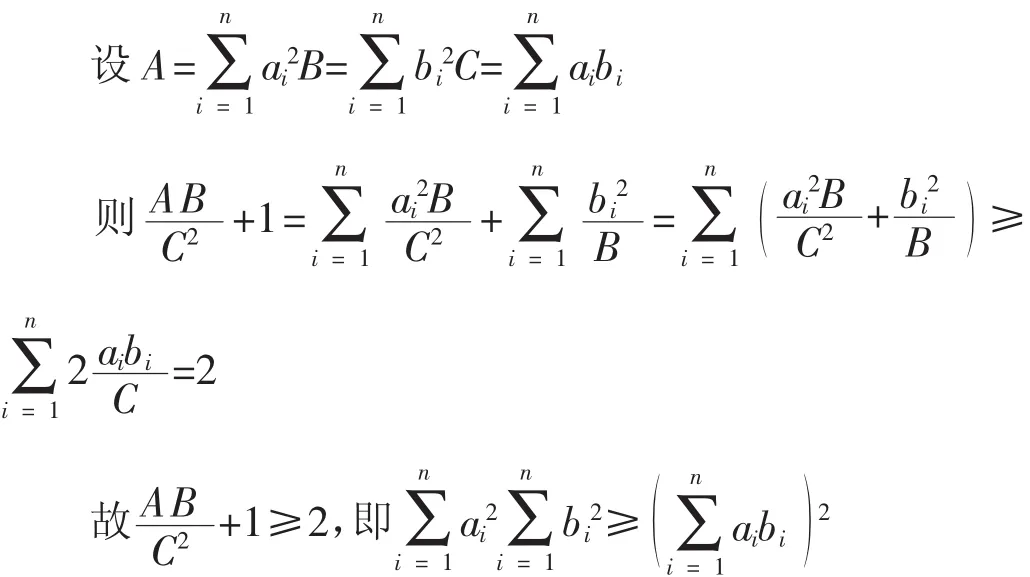
方法2（二次型法）

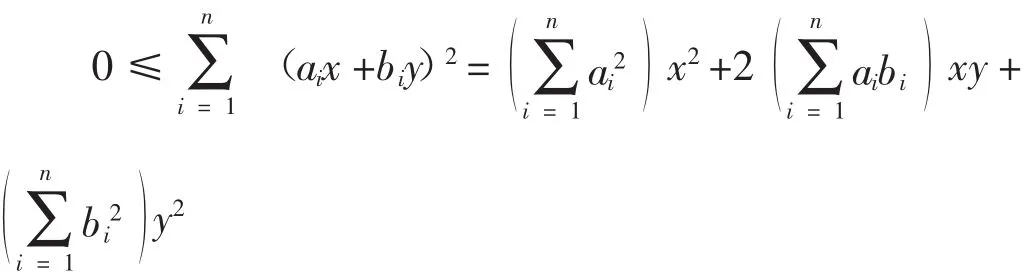
由常识可知，上式的二次型是关于x与y的非负函数，故有

成立

证明方法3（数学归纳法）

当n=1时显然成立

其中的等号当且仅当a1b2=a2b1时成立

那么当n=k+1时

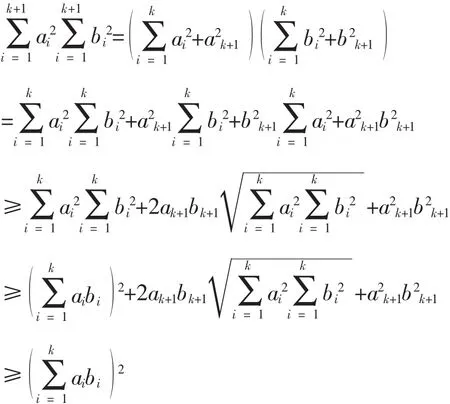
其中等号当且仅当aibj=ajb（ii，j=1，2，…，k）时成立。

二、柯西不等式的简单应用

柯西不等式是一个非常重要的不等式，学习柯西不等式可以提高我们的数学探究能力、创新能力等，能进一步开阔我们的数学视野，培养我们的创新能力，提高我们的数学素质。在合适的场合，灵活巧妙地运用它，可以使一些使用平常方法不易解开的难题迎刃而解。这个不等式结构宽松，应用灵活广泛，常通过适当配凑，直接套用柯西不等式解题，常见的有两大类型：

例1 已知正数a，b，c满足a+b+c=1。求证：a3+b3+

证明：利用柯西不等式：

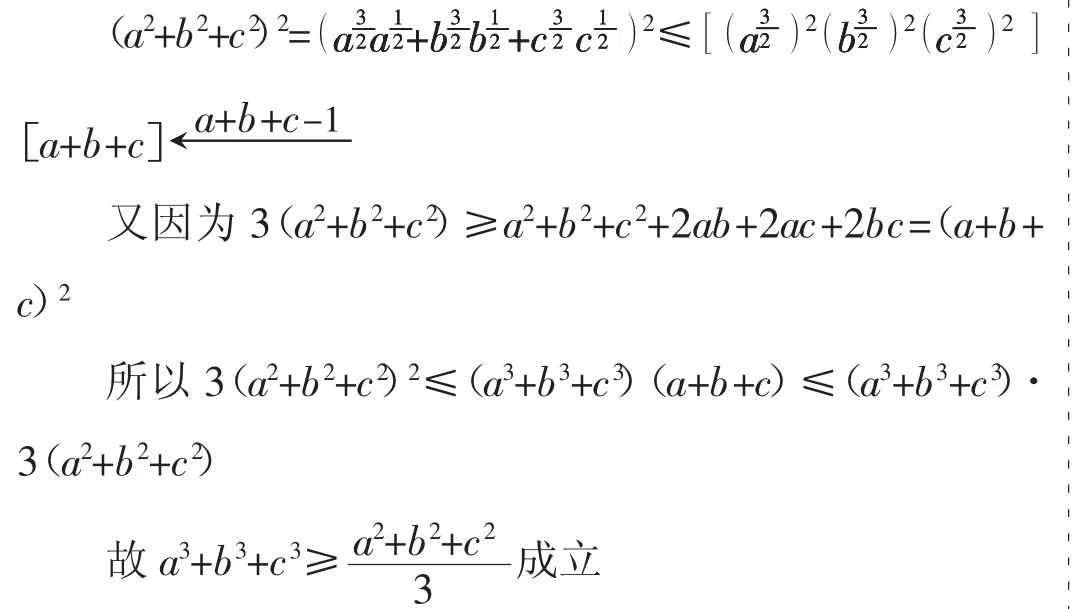
例2 三角形外接圆问题

设P是△ABC内部的一点，x，y，z是点P到三角形三边a，b，c的距离。R是△ABC外接圆半径，求证：

证明：由柯西不等式得到

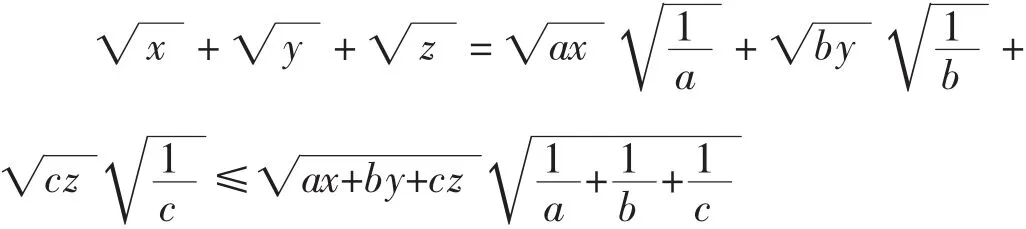
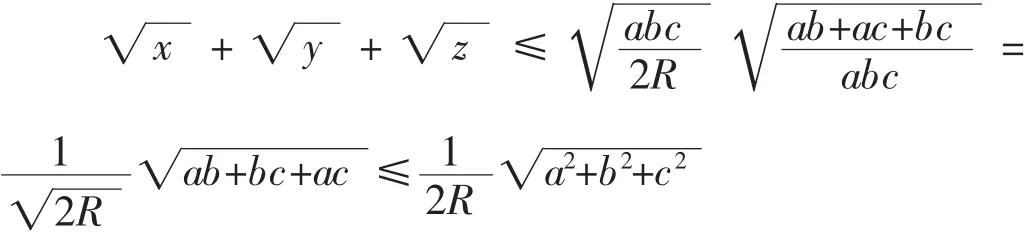
故有上式成立。

三、证明光行最短原理

在几何光学中，有费尔马发现的一个著名的光行最短原理。现在重新叙述一遍：设甲、乙两种均匀介质的分界线为直线l，光线从甲种介质中一点A出发，经过l上的点O折射后到乙种介质中一点B，所用的时间为tO，P是l上任一点，光线从A经过P到达B的时间为tP，求证tP≥tO，其中等号当且仅当P与O重合时成立。

证明：以l为x轴，O为原点，建立直角坐标系。设A，B，P 的坐标分别为（x1，y1），（x2，y2），（x，0），光线的入射角为∠1，折射角为∠2（如图），在甲、乙两种介质中光速分别为 v1，v2，

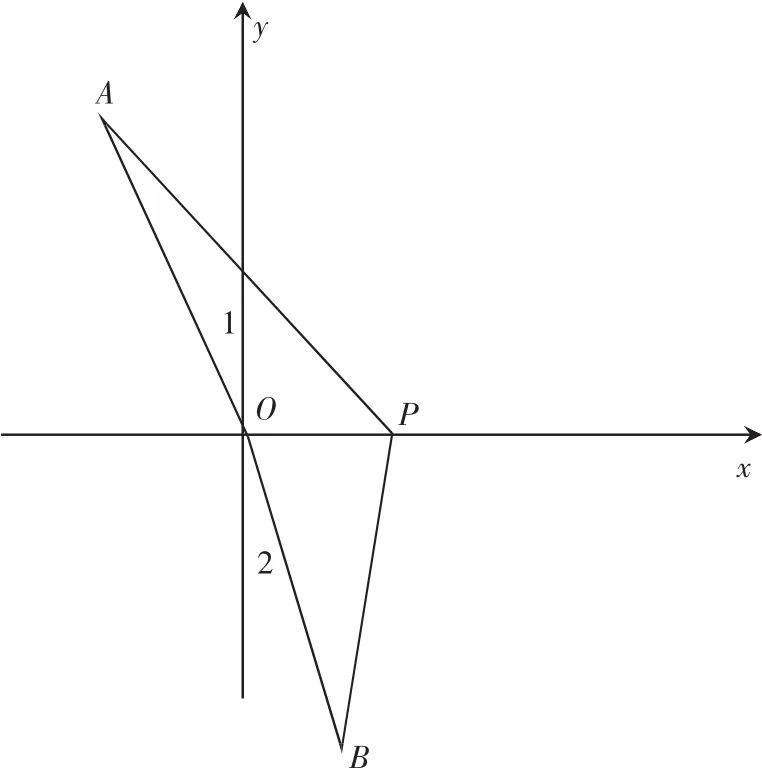
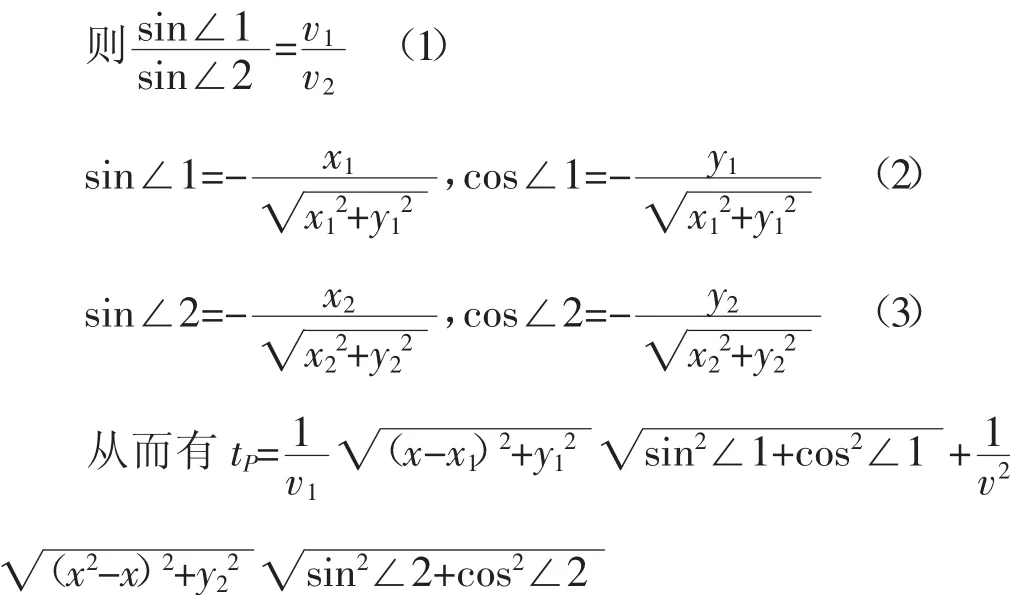
由柯西不等式：

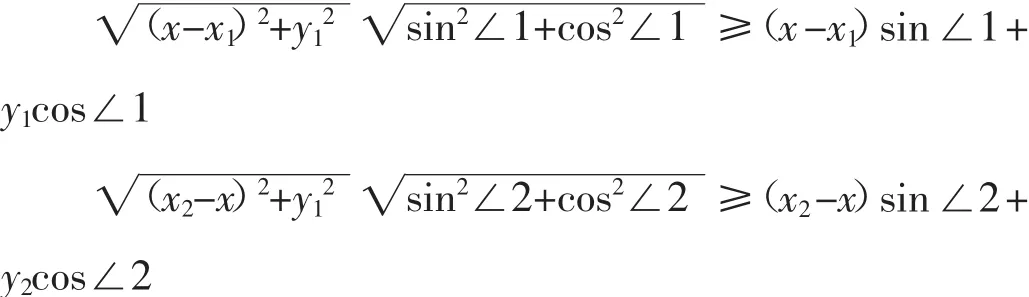
将上面两个不等式左右两边同时除以v1，v2后，再将两式相加，之后得到

让等号成立的充分必要条件是

（x-x1）cos∠1=y1sin∠1

（x2-x）cos∠2=y2sin∠2

也就是x=0

原命题得证。