直觉模糊熵的改进及其在应急决策中的应用

陈业华，黄 璐

（燕山大学 经济管理学院，河北 秦皇岛 066004）

0 引言

近年突发危机事件频发已经对社会和人们的生命财产安全造成极大的威胁，比如印度孟买11.26恐怖袭击事件，日本福岛核泄漏事故，我国的5.12汶川特大地震灾害、三鹿婴幼儿奶粉事件，8.12天津滨海新区爆炸事故等，突发事件的突发性、紧急性、严重性、群体爆发性、蔓延性等特征对政府和社会带来极大挑战，随着我国经济的快速发展，自然灾害、社会安全事故等各类型的突发事件频繁发生，其影响范围广、破坏性强、过程复杂度高、应对难度大[1]，使得建立科学的应急决策机制迫在眉睫。应急决策是在不确定条件下对各种突发事态进行准确分析与判断并及时采取处置措施的决策行为，是当其发生时，能够在短时间内收集到有关的决策信息并及时予以处理，同时确定相关的决策问题及目标，拟定切实可行的决策方案，并从中选择出较为满意的方案，在此基础上组织实施并监督检查，纠正决策过程当中的偏差及失误，直到决策问题完全予以消除的动态演化过程[2]。

目前，如何在有限的事件内有效地应对突发事件的发生与发展已引起国内外学者的巨大关注，许多学者从不同的角度、利用不同的工具方法对应急决策给予了诸多研究，但是由于突发危机事件的特性致使决策者所获得的有效信息十分有限，决策需要信息。有效信息量越多越有利于决策者做出正确的决策，信息收集的不完全以及决策者认知能力的限制，在实际的决策当中往往会出现模糊与不确定信息。在现有文献的直觉模糊熵基础上[3-14]，综合考虑隶属度和非隶属度的偏差以及犹豫度的影响，构建了一种改进的直觉模糊熵，可适用于某些模糊度无法区分的特殊情形。应用直觉模糊熵的定义对改进的直觉模糊熵进行了推导与证明，并与现有的直觉模糊熵进行了对比分析，验证了该公式的正确性，同时，对于方案属性权重全部未知的决策问题，给出了一种解决方法，并将其应用到突发事件应急决策中，为决策者快速、高效、准确地做出决策提供一种新的思路和途径。

1 直觉模糊集及其相关概念

传统的模糊集只包含一个隶属度参数，应对复杂决策时所含信息比较片面，直觉模糊集在原有参数信息上添加了非隶属度参数。此外，犹豫度可以体现模糊信息的未知度，这三个参数对于客观事物的模糊本质能够更加细致全面的描述，因此得到了广泛的应用和推广。

定义1[5]：设X为一个非空集合，则X上的一个直觉模糊集为，其中uA(x) 和νA(x)分别为X中元素x属于A的隶属度，非隶属度,且满足条件

定义2[5]：设X中的任一直觉模糊数，如果，则πA(x)称为X中元素x属于A的犹豫度，显然

将非空集合X上的直觉模糊集A作为全部直觉模糊数的集合，记为IFS(X)。

定义3[5，15]：对于两个直觉模糊集和,定义它们之间的关系如下：

（1）A⊆B当且仅当(xi)≤uB(xi)，νA(xi)≥νB(xi)，uA∀xi∈X ；

（2）A=B当且仅当A⊆B和B⊆A；

定义4[6]：一个映射 E:IFS(X )→[0 ，1]称为直觉模糊熵，如果E满足以下条件:

（1）E(A)=0当且仅当A是经典集；

（2）E(A)=1当且仅当∀xi∈X，满足uA(xi)=νA(xi)；

（3）E(A)=E(AC)；

（4）E(A)≤E(B )，B的模糊性大于A，∀xi∈X。

由定义4可知，当uB(xi)≤νB(xi)时，有uA(xi)≤uB(xi)，νA(xi)≥νB(xi)；当 uB(xi)≥νB(xi)时 ，有 uA(xi)≥uB(xi)，νA(xi)≤νB(xi)。

直觉模糊熵可有效度量模糊信息的模糊程度，能够应用不明确的数据从两个方面较为完善的表达模糊对象，可将其视为集合X中元素x的不确定程度和未知度，对于两个直觉模糊集A，B∈IFS(X )，当 |uA(x)-νA(x) |=|uB(x)-νB(x)|时，若 π(x)越大则表明对x的未知程度较高，即模糊程度越高，则熵值应该越大，反之亦然；若|uA(x)-νA(x)|≠|uB(x)-νB(x)|时，|u(x)-ν(x)|越小即两者越接近时则表明对x不确定程度较高，认识比较模糊，其熵值应该越大，反之亦然。由此更加直观的判断直觉模糊熵值大小，体现出隶属度、非隶属度及犹豫度对熵值的贡献。

2 直觉模糊熵定义存在的不足

对于以往提出的直觉模糊熵定义存在两点不足，现分析如下：

（1）在直觉模糊熵定义中未充分体现犹豫度因素对熵值的影响

对任意的直觉模糊集A∈IFS(X )，Ye[7]等定义的直觉模糊熵为：

Zhang[16]对上式进行了优化，给出了如下直觉模糊熵：

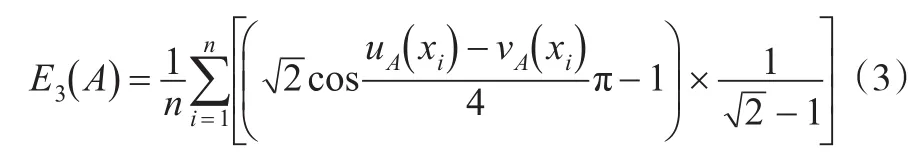
Verma[8]等定义的直觉模糊熵为：

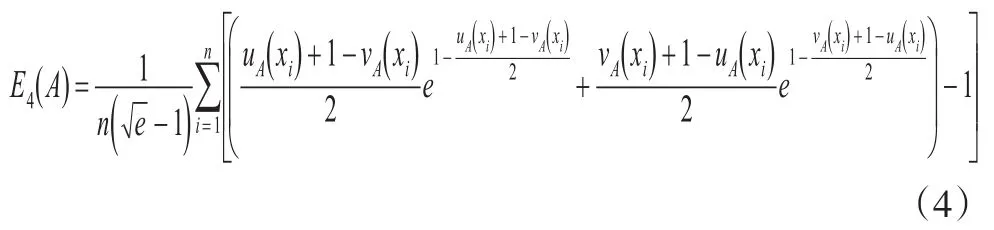
在式（1）至式（4）中，uA(xi)与 νA(xi)体现的是直觉模糊集的不确定性，而没有包含体现犹豫度对熵值的影响因素πA(xi)。由于决策环境的影响，人类认知能力的限制，对于客观世界的认识是不完全的，存在很强的未知性，需要用πA(xi)来体现，不考虑πA(xi)对直觉模糊熵值的作用是不全面的，同时对于隶属度与非隶属度差值相等的情况不能有效区分。下面举一个例子来说明这点。

例1：设A=(0.3,0.1)，B=(0.5,0.3)，利用式（1）至式（4）计算得到E1(A)=E1(B)=E2(A)=E2(B)=E3(A)=E3(B)=0.9580；E4(A)=E4(B)=0.9618，可见A的模糊性要大于B，即当|uA(x)-νA(x)|= |uB(x)-νB(x )|时，犹豫度值越大则熵值越高，但应用式（1）至式（4）得出的熵值却相同，这与人们的直觉相悖，并不符合事实。由此可见定义式（1）至式（4）不能区分隶属度与非隶属度偏差相等的情形。

（2）考虑了犹豫度对直觉模糊熵的影响，但对某些情形（如例2）未考虑全面

对任意的直觉模糊集A∈IFS(X )，Szmidt等[6]定义的直觉模糊熵为：

上述的直觉模糊熵的定义式引入了犹豫度πA(xi)，但是对于某些特殊情形却不能有效区分，下面举一个例子来说明这点。

例2：假设A=(0.3，0.5)，B=(0.16，0.4)，利用式（5）至式（7）计 算 得 到 E5(A)=E5(B)=0.7143;E6(A)=E6(B)=0.7143,E7(A)=0.7647，E7(B)=0.8293，根据直觉模糊熵性质可知，计算的结果不合理。因为当 |uA(x)-νA(x) |≠|uB(x)-νB(x) |时，A与B隶属度与非隶属度越接近，其模糊程度越高，则熵值应该越大，而式（5）、式（6）结果显示A的模糊性等于B，式（7）结果显示A的模糊性小于B。

3 直觉模糊熵的改进

针对已有直觉模糊熵定义中存在的不足，引入能够充分考虑犹豫度的影响因子1-πA(xi)，定义一个新的直觉模糊熵表达式。对于任意的直觉模糊集A∈IFS()X ，定义直觉模糊熵为：

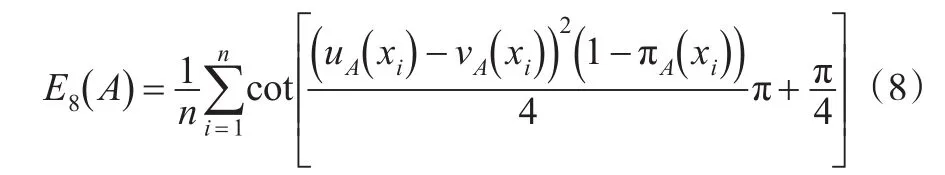
对于定义式（8），只要满足定义（4）中熵的四个条件，即可证明式（8）的正确性和合理性。现证明如下：

对于条件（1），若 E8(A)=0,则可明显得出,即=1，由此可得 πA(xi)=0从而可推出uA(xi)=0，νA(xi)=1，或uA(xi)=1，νA(xi)=0，即A为经典集；若A为经典集，很明显E8(A)=0，条件（1）得证。

对于条件（2），若 E(A)=1,则

8=0，可得 πA(xi)=1或uA(xi)=νA(xi),若 πA(xi)=1，于是uA(xi)+νA(xi)=0，即 uA(xi)=νA(xi)=0，由此可得uA(xi)=νA(xi)；反之显然成立。条件（2）得证。

条件（3）得证。

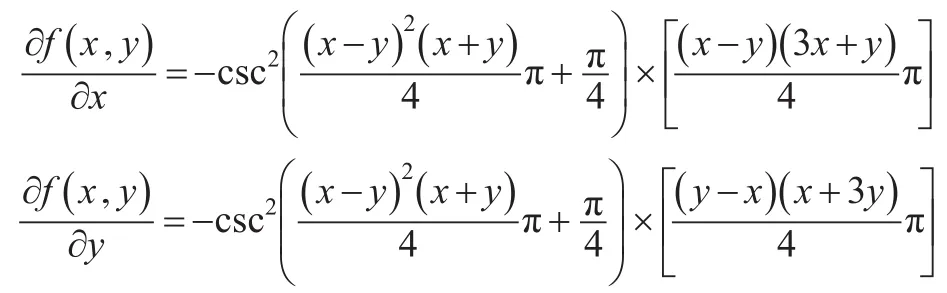
即E(A)≤E(B)。因此E8(A)≤E8(B )，条件（4）得证。证毕。

直觉模糊熵的定义式（8）比式（1）至式（7）更为全面合理，主要表现在如下几个方面：

（1）一个有效的直觉模糊熵的定义式，除了具有较好的精确度之外，还应该具有有效的区分度，式（8）不仅考虑隶属度、非隶属度的偏差，而且还充分包含决策者的犹豫度，从不确定性和未知性两方面更加全面客观地体现出了模糊集的模糊程度，这样得出的结果对于决策就会更为有利。

（2）对于未考虑犹豫度对直觉模糊熵值的作用，无法有效区分隶属度、非隶属度偏差相等的情形，针对例1，利用定义式（8）计算得到E8(A)=0.9752，E8(B)=0.9510，A的模糊性大于B，这个结果是合理和正确的。

（3）对于一些无法区分的情形，此公式可以做到有效区分，针对例2，利用定义式（8）计算得到 E8(A)=0.9510，E8(B)=0.9504，A的模糊值大于B，这个结果与直觉更相符。

4 改进的直觉模糊熵在应急决策中的应用

突发危机事件环境下，决策者获取的决策信息往往都是不可靠、不完全的，改进的直觉模糊熵由于充分考虑了应急决策信息的模糊度以及决策者的犹豫度，有效地减少了人为主观因素对决策的影响，因此在应急决策中更能发挥其作用。设是由m个应急决策方案组成的方案集，是由n个应急方案属性组成的属性集，属性权重为方案 Ai在属性 pj下的属性值是一个直觉模糊数，其中0≤uij≤1，0≤νij≤1，0≤uij+νij≤1。

4.1 属性权重的确定

在应急决策领域，考虑侧重点的应急决策才是真正客观有效的决策，属性权重wj值的大小可有效表达不同属性在应急方案中的相对重要程度，能够对不同属性在其中所起的作用进行区别对待。设是一直觉模糊矩阵，对任意的直觉模糊数，由定义式（8）可计算其直觉模糊熵，记为eij，若eij值越大则说明其模糊性越大，令，则属性权重wj可由下式计算:

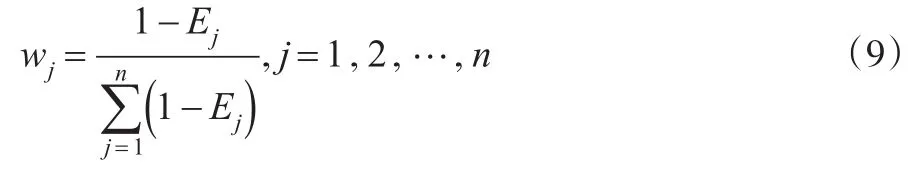
直觉模糊熵作为刻画应急决策信息模糊程度的有效测度手段，其熵值越高表明获取的决策信息模糊程度越大，为了减少对应急决策精度和可靠度的影响，其对应的属性权重就应该越小，相反则越大，wj值充分考虑了信息模糊度以及犹豫度对决策方案的影响，存在较强的客观性。

4.2 基于考虑交叉影响的直觉模糊加权平均算子

考虑到突发事件爆发具有不稳定性、发展性、未知性等特征，应急决策与普通的管理决策不同，其受到各种因素的多重附加影响，决策方案的属性权重从不同的侧面对决策对象的重要程度进行了定量分配，并以此为基础，结合突发事件环境下模糊性信息，得出应急决策方案的综合评价值。

依据文献[16,17]，结合定义2和定义3，可定义改进的直觉模糊数的基本运算法则：

定义5：设X为给定的有限论域，A，B∈IFS(X )，定义直觉模糊集上的乘法、数乘及幂运算法则：

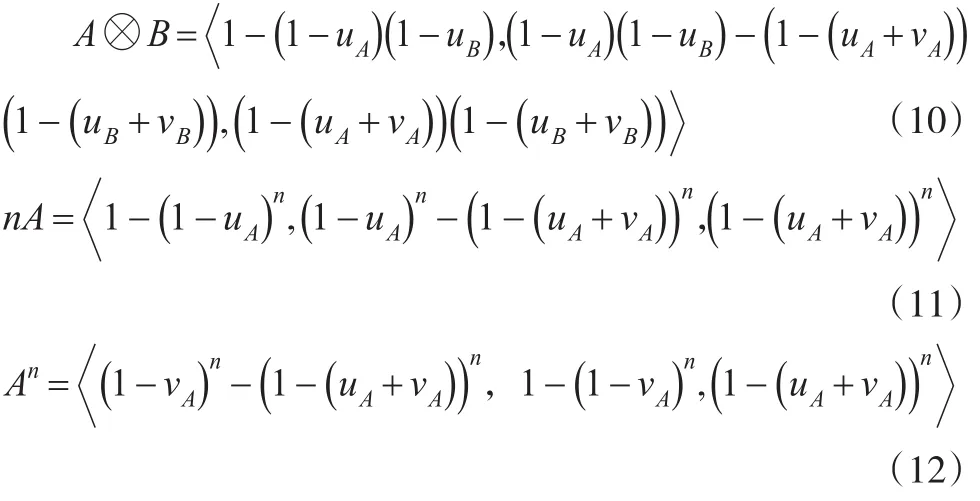
定义5中运算法则不仅考虑了隶属度与非隶属度的交叉影响，同时还增加了犹豫度，由定义5，进一步定义n维直觉模糊加权平均算子。

定义6：设X为给定的有限论域，Ai∈IFS(X )，i=1，2，…，n，令：

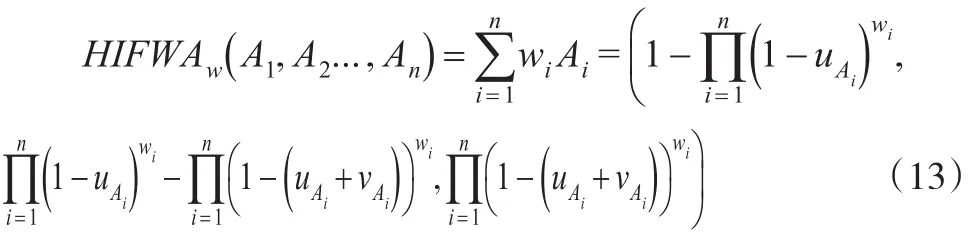
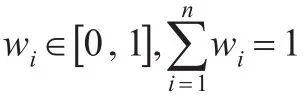
其中wi为其权重，且满足，则称HIFWAw为n维直觉模糊加权平均算子。

由定义6可算得综合直觉模糊评价值。由于s(α)能充分体现隶属度、非隶属度及犹豫度的相关信息及相互之间的交叉作用，同时H(α)仍为直觉模糊数，减少了决策信息的丢失，因此得出的综合评价值更加灵活、全面，为决策者在有限的时间内做出有效的决策提供依据，满足应急决策的需求。

4.3 评价函数的构建

应急决策最重要的是时间，且对决策方案的精度要求很高，为了便于决策者快捷直观的判断应急决策方案的优劣，并从中选出最为满意的应急方案，在应用HIFWAw计算得出决策方案的综合评价值之后，构建如下的评价函数来评价应急决策的精度，同时节省必要的时间。在文献[18]提出的记分函数S(α)=uA(x)-νA(x) ，以及文献[19]定义的精确度评估函数H(α)=uA(x)+νA(x)的基础上，添加一个可变系数ζ，定义如下记分函数s(α)和精确度评估函数(α)。

定义7：对于直觉模糊数 α=(uA(x)，νA(x) )，定义(α)为记分函数，H(α)为精确函数。这里：

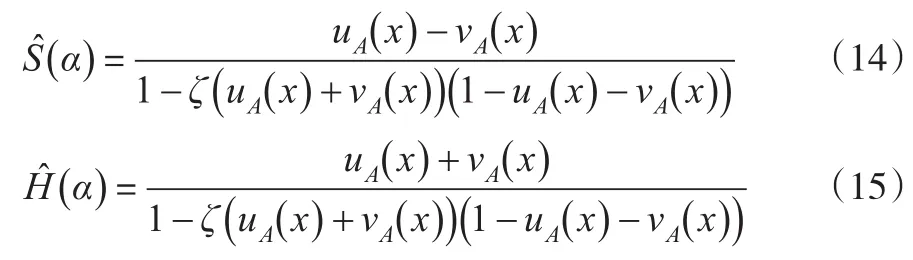
式（14）、式（15）中，ζ∈[0 ，1]，ζ表明应急决策方案的可信度，当ζ＞0.5时，表明决策者对应急方案较为满意，即认为决策方案的可信度较高；当ζ＜0.5时，则表明决策者认为决策方案的可信度较差，通过较小的ζ值来减小此方案的评价函数值，以此来降低对最终决策方案优劣排序结果的影响；当ζ=0.5时，表明决策者对于此方案是保持中立的，一般取ζ=0.5。

根据Xu和Yager[20]给出的任意两个模糊数a1和a2之间的关系，基于定义7中的记分函数和精确度评估函数，定义其评价准则为：若，则 α1＞ α2；若，且，则 α1＞ α2；若，且则 α1= α2

考虑到应急决策环境下有效信息的缺失，以及决策者个人偏好的影响，通过ζ值的大小，对决策方案的可信度进行区分，从而最终实现应急方案的优劣排序。

针对以上内容，给出改进直觉模糊熵在应急决策应用当中的具体计算步骤如下：

步骤2：采用式（8）可得出每个模糊数aij的直觉模糊熵，并由式（9）得出各应急方案的属性权重wj(j=1，2，…，n)；

步骤3：引入wj应用式（13）得出各应急决策方案的综合直觉模糊评价值HIFWAw；

步骤4：由HIFWAw可得出各个方案的得分函数值(αi)(i =1，2，…，m )，根据(αi)值对应急方案进行优劣排序，(αi)越高，则表明决策者对于此方案越满意即其越优；

步骤5：如果存在(αi)=(αj)，进一步计算精确函数(αi) 、(αj)来判断方案的优劣；

步骤6：形成应急方案的完整排列次序，从而选出最优的方案。

5 算例分析

以四川省雅安市卢龙县某处地震灾害发生后的一居民区为例进行应急决策。在地震灾害发生后，为了保护公民的利益及人身安全，除对灾区人民进行精神安抚之外应尽快为他们建设自己的家园，决策者需在有限的时间内尽快做出应急决策，对于居民区灾后处置,设有四个备选方案Ai(i=1，2，3，4),A={修缮 (A1),重建 (A2)，修缮+重建(A3),搬迁(A4)},采用六个评价指标（属性）Pj(j=1，2，3，4，5，6)对方案进行评价，P={成本大小 (p1),可行性 (p2)，安全性(p3)，后期保养费用(p4)，房屋受损程度(p5)，相关设施受损程度(p6)}，假设方案Ai(i=1，2，3，4 )在属性Pj(j=1，2，3，4，5，6) 下的评价数值用直觉模糊集给出，相应的直觉模糊数aij如表1所示。（这里aij本质上为不同决策方案关于地震灾害不同特征属性的隶属度和非隶属度，一般地，这个数值由应急决策者或者应急决策领域的专家依据地震灾害的实时情景或者以往类似事件统计数据给出。ζ=0.5）。

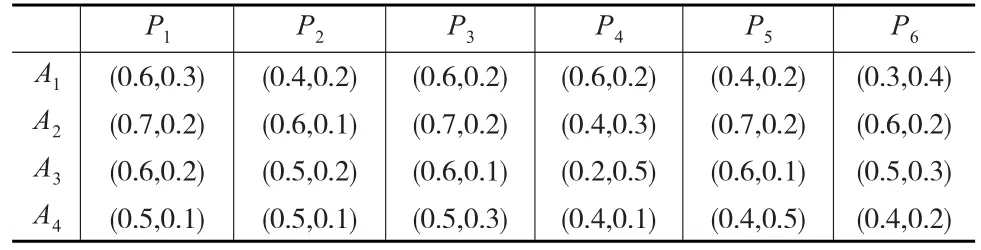
表1 各应急决策方案的直觉模糊评价值

步骤1：构造决策矩阵

步骤2：计算属性权重

由公式（8）得到矩阵Q中每一模糊数的直觉模糊熵，结果如表2所示。

表2 直觉模糊熵计算结果

利用式（9）得到的各属性权重为：

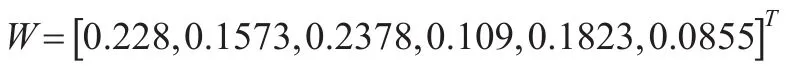
步骤3：利用公式（13）计算每一方案的集成评价值HIFWAw：

即方案2＞方案3＞方案1＞方案4，说明重建应该为最优方案，其次为重建与修复同时进行，再次为修复，最次为搬迁。

6 结论

本文针对突发危机事件的特点，在对现有文献直觉模糊熵进行分析的基础上，构造了一种改进的直觉模糊熵，并将其应用到突发事件应急决策当中，得出以下结论:（1）利用改进的直觉模糊熵，依据应急环境下信息的模糊性，能够从不确定性和未知性两方面对模糊信息进行全面有效的刻画，在一定程度上提高了决策结果的精确度和客观性;（2）验证了改进直觉模糊熵应急决策方法的结果仍为直觉模糊数，能够最大限度的减少决策信息的丢失;（3）通过对地震灾后处置应急决策算例的分析可知，决策信息的不确定程度和未知度直接影响应急方案综合直觉模糊评价值的大小，将最终决定决策方案的优劣，应用此方法能为决策者迅速有效地确定最优应急方案及其优劣排序，提高决策效率。但本文对应急决策的讨论还不够深入，未能实现根据灾情的变化对应急方案进行动态调整，特别是决策者的心理、政府的建议等均考虑的不够充分，有待进一步研究。