广义直觉模糊有序加权扩展相似度算子及其应用

王琦峰，孙海宁

（浙江万里学院，浙江 宁波 315100）

0 引言

自Zadeh（1965）[1]提出模糊理论以来，因其能较好地处理模糊信息的优势而被广泛应用在控制系统、机器学习、多属性决策等多个领域。Atanassov（1986）[2]在传统模糊理论的基础上进行扩展，提出了直觉模糊集的概念。直觉模糊集同时考虑隶属度、非隶属度和犹豫度这三个方面的信息，能更好地描述客观事物的模糊性，因此有关直觉模糊理论的研究日益增多。目前在直觉模糊环境下，采用直觉模糊数表征其相似度的研究相对较少，为了更准确地刻画决策问题的模糊特性，本文提出一种新的直觉模糊相似度计算方法，并将其与GIFOWA算子相结合，提出广义直觉模糊有序加权扩展相似度（GIFOWES）算子，研究了其性质以及各种特殊形式，并提出了基于此算子的群决策方法，通过实际案例证明方法的有效性。

1 基础理论

本文主要介绍直觉模糊集的相关理论知识，包括直觉模糊集的概念、运算法则以及相关算子。

定义1[2]：集合X下的直觉模糊集：

其中μA(x)为隶属度，νA(x)为非隶属度，πA为犹豫度，πA=1-μA-νA。 (μA，νA)被称为直觉模糊数，每个直觉模糊数可简单地写成，μα，να∈[0，1]且0≤μα+να≤1。

为了比较两个直觉模糊数之间的大小关系，Xu和Yager（2006）[3]分别定义了得分函数S(α)=μα-να和精确函数H(α)=μα+να。对于两个直觉模糊数之间的比较可采用如下形式：

设α=(μα，να)，β=(μβ，νβ)为两个直觉模糊数。

（1）若S(α)＞S(β)，则α＞β；

（2）若S(α)=S(β)，则：①若H(α)=H(β)，则α=β；②若H(α)＞H(β)，则α＞β；③若H(α)＜H(β)，则α＜β。

对于任意三个直觉模糊数，α=(μα，να)，α1=(μα1，να1)和α2=(μα2，να2)，其运算公式[4]如下：

定义2[5]：设Aj=(μj，νj)(j=1，2，...，n)是直觉模糊集。GIFOWA算子为一个n维映射，GIFOWA：Ωn→Ω。

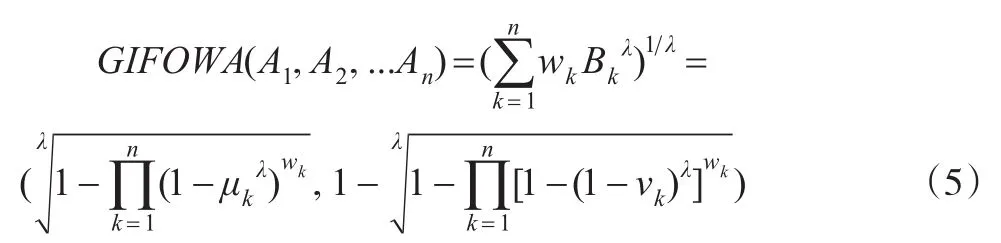
其中，w=(w1，w2，...，wn)是位置权重；λ＞0 为参数；Bk=(μk，νk)(k=1，2，...，n) 为Aj=(μj，νj)(j=1，2，...，n) 的第k大的元素。

2 广义直觉模糊有序加权扩展相似度算子

由于直觉模糊数自身包含隶属度、非隶属度和犹豫度，反映了一定的犹豫程度，其相似度也应当表现出一定的模糊性。而传统的直觉模糊相似度公式计算结果都是精确数，未能体现这一模糊性，针对这一不足，张洪美等（2007）[6]提出一种新的相似度概念，定义如下：

定义3[6]：s:Ω2→Ω，其中Ω为X上所有直觉模糊集的集合，且设 Ai∈Ω(i=1，2，..，n)，若 s(A1，A2)满足条件：

（1）s(A1，A2)是直觉模糊数；

（2）s(A1，A2)=(1，0)当且仅当 A1=A2；

（3）s(A1，A2)=s(A2，A1)；

（4）如果 A1⊆ A2⊆ A3,则s(A1，A3)⊆ s(A1，A2)且s(A1，A3)⊆s(A2，A3)；

则称s(A1，A2)为A1和A2的直觉模糊相似度。

近年来，很多学者提出了直觉模糊集和区间值模糊集本质上是模糊集的一种广义形式，只是两种表达方式不同[7]。因此，直觉模糊集和区间值模糊集的很多方法理论存在联系。

对于任意直觉模糊数，α=(μα，να)，则其犹豫度为πα=1-μα-να，因此直觉模糊数 α ，它的隶属度下界为μα，上界为πα+μα。因此，直觉模糊数α可以表示为[μα，μα+πα]，也可以表示为[μα，1-να][8]。因此本文从区间值模糊数的角度构建相似度。

定理1：设A1，A2为两个直觉模糊集，令：

其中，α≥0，β≥0，α+β=1。存在α*，β*，使得maxh=h*，即：

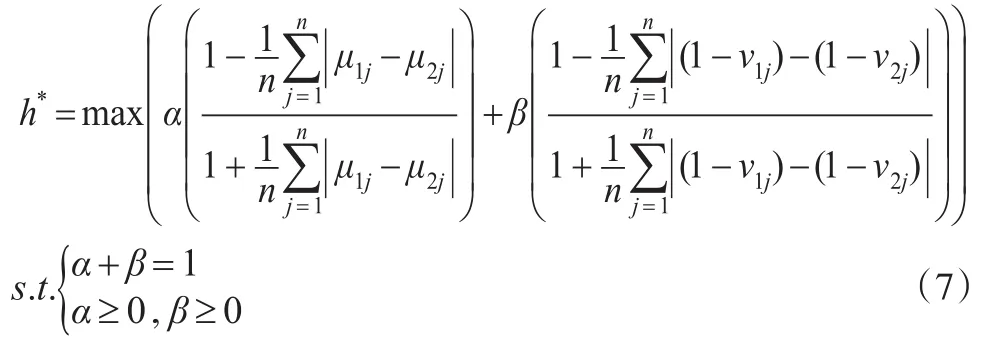
同样存在 α*，β*，使得 minh=h*，即：

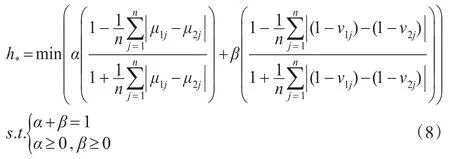
根据上述公式，提出直觉模糊数相似度公式为：

下面证明上述相似度公式，符合相似度的四个条件。

（1）先证明s(A1，A2)为直觉模糊数形式

因为α+β=1，则有：

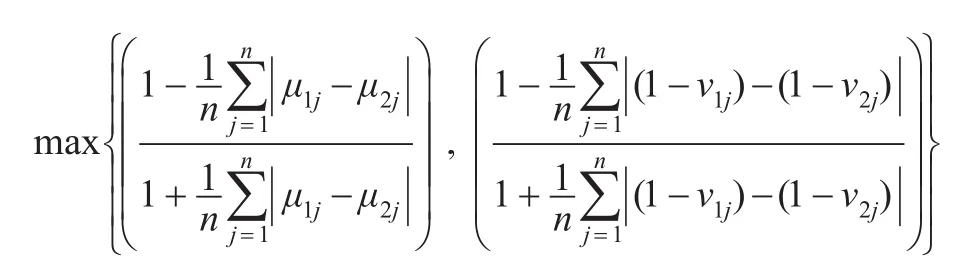
因为：

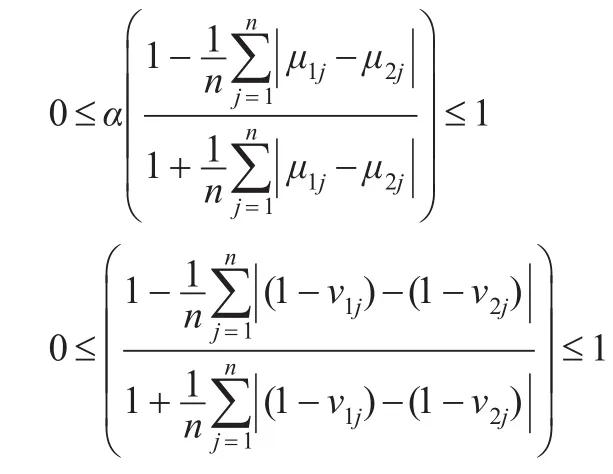
则0≤h*≤1。

（2）snew(A1，A2)=(1，0) 当且仅当 A1=A2；

必要性

由s(A1，A2)=(1，0)可知,h*=h*=1,则μ1j=μ2j,则ν1j=ν2j,所以A1=A2。

充分性

由 A1=A2，可知 μ1j=μ2j，ν1j=ν2j，则 h*=h*=1，故s(A1，A2)=(1，0)。

（3）显然成立。

（4）如 果 A1⊆A2⊆A3，μ1j≤μ2j≤μ1j，ν1j≥ν2j≥ν2j,(1-ν1j)≤(1-ν2j)≤(1-ν2j)。

因为：

所以：

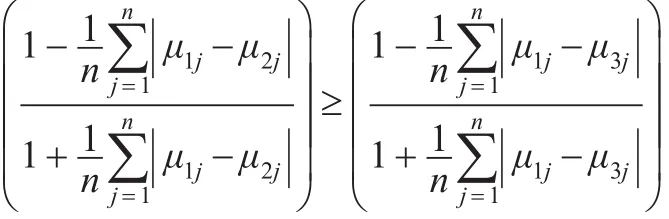
同理：

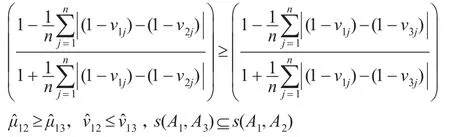
同理 s(A1，A3)⊆ s(A2，A3)。

例1：设 α=(0.5，0.5)，β=(0.4，0.2)，利用上述相似度计算方法计算其相似度。

h*=0.82;h*=0.54

snew(α1，α2)=(0.54，0.18)

在一些实际的经济管理决策问题中，不同的元素的重要性可能不完全一样，因此需要赋予不同的权重.假设集合中元素 μj的权重为 wj(j=1，2，...，n)，要求满足归一化条件，即。将式（6）中融入元素的权重，可得到直觉模糊集A1，A2的加权相似度。

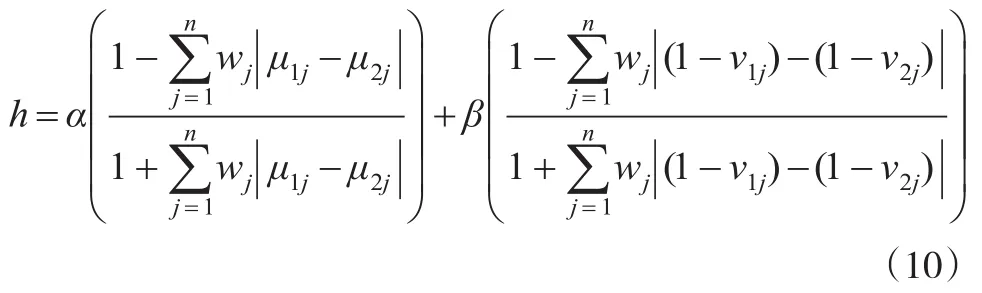
其中，α≥0，β≥0，α+β=1。

设h*=maxh，h*=minh

定义4：设 A=(a1，a2，...，an)B=(b1，b2，...，bn)为两个直觉模糊集，GIFOWES算子是一个n维映射，GIFOWES：Ωn→Ω：

其中 w=(w1，w2，...，wn)为相关联(位置)权重，wj∈[0，1]，=1σ(1)，σ(2)，...，σ(n)是 (1，2，...，n)的一个置换，对于任意的j，满足为参数，且 λ∈R，λ≠0。

例2：A=(a1，a2，a3，a4)={(0.3,0.2),(0.7,0.1),(0.5,0.4),(0.3,0.5)},B=(b1，b2， b3，b4)={(0.5,0.1),(0.6,0.2),(0.9,0.1),(0.7,0.3)} 为两个直觉模糊集，相关联权重 wj=（0.2，0.3，0.2，0.3）。利用GIFOWES(A,B)计算它们之间的相似度。

首先，利用新直觉模糊相似度计算对应直觉模糊数的相似度，如下：

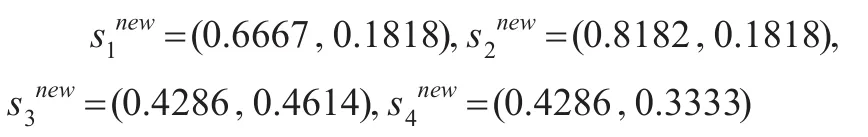
对上述结果按得分函数大小进行排序得：

设 λ=1时，GIFOWES(A，B)=(0.6362，0.2627)。

下面介绍GIFOWES的相关性质:

定理2（交换性）：A=(a1，a2，a3，a4)B=(b1，b2，b3，b4)两个直觉模糊集。

GIFOWES(A，B)=GIFOWES(B，A)

定理 3（单调性）：A=(a1，a2，a3，a4),B=(b1，b2，b3，b4),C=(c1，c2，c3，c4) 两 个 直 觉 模 糊 集 。 如 果 对 于 任 意(j=1，2，...，n)snew((aj，bj))≥snew((aj，cj))则有:

GIFOWES(A，B)≥GIFOWES(A，C)

定理4（幂等性）：A=(a1，a2，a3，a4)B=(b1，b2，b3，b4)两个直觉模糊集。如果对任意的snew((aj，bj))的相似度相等snew((aj，bj))=s0，则有：

定理5（有界性）：A=(a1，a2，a3，a4)B=(b1，b2，b3，b4)两个直觉模糊集。如果最大相似度majx snew(aj， bj)=smax， 最小相似度mjin snew(aj，bj)=smin，则有：

在GIFOWES中，通过改变公式中的参数λ和权重向量，可以得到不同形式的GIFOWES算子，例如：

（1）当λ=1，GIFOWES退化为直觉模糊有序加权扩展算术相似度（IFOWES）算子：

（2）当λ=2，GIFOWES退化为直觉模糊有序加权扩展二次相似度（IFOWQES）算子：

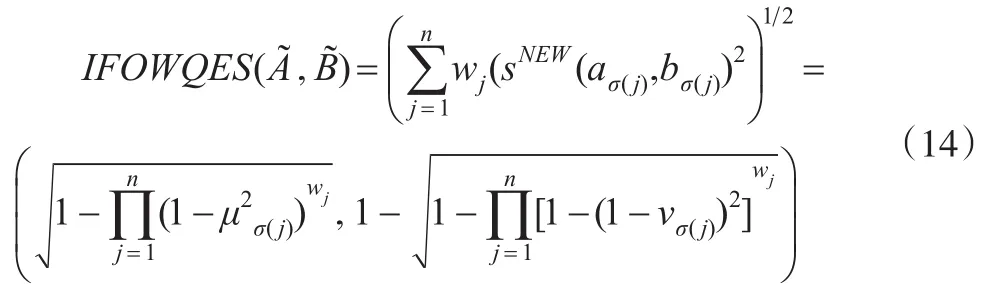
（3）当λ→0，GIFOWES转化为直觉模糊有序加权几扩展何相似度（IFOWGES）算子：

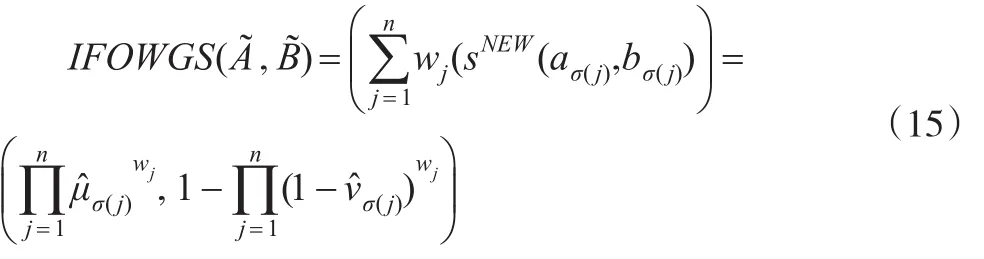
从权重角度，可以得到GIFOWES的其他特殊形式，如：

（1）当 w1=1，wj=0(j≠1)时，可以得到直觉模糊最大相似测度（GIFMAXES）算子；

（2）当 wn=1，wj=0(j≠n)时，可以得到直觉模糊最小相似测度（GIFMINES）算子；

（3）更一般，当 wk=1，wj=0(j≠k)时，可以得到位置直觉模糊相似度（Step-GIFOWES）算子；

（4）当 w1=wn=0，wj=1/(n-2)，(j≠1，n)时，可以得到奥林匹克直觉模糊相似（Olympic-GIFOWES）算子。

3 基于广义直觉模糊有序加权扩展相似度算子的群决策方法

考虑直觉模糊环境下的多属性（指标）综合决策问题，设 A={A1，A2，...，Am}为方案集，e={e1，e2，...，et}为评价专家集，G={G1，G2，...，Gn}为属性（指标）集，ω=(ω1，ω2，...，ωn)为各属性的权重，w=(w1，w2，...wt)为相关联（位置）权重。专家ek∈e对方案Ai∈A关于指标Gj∈G进行评价，从而构成直觉模糊评价矩阵为直觉模糊数。基于GIFOWES算子的群决策步骤如下：

步骤1：专家根据评价矩阵，给出期望的理想方案。如表1所示。

表1 理想方案

步骤2：利用式（10）和式（11）计算各个专家评价矩阵与理想方案之间的相似度，形成相似度矩阵sm。

其中sik=snew(ri(k)，R*)表示专家ek对Ai评价的数组ri(k)=(μij(k)，νij(k))1×n(i=1，2，..，m) 与 其理想方案R*=(r1*，r2*，...rn*)之间的相似度。

步骤3：利用GIFOWES算子集结各个专家关于Ai的相似度。候选方案Ai的最终相似度Ri。

步骤4：根据Ri的大小进行排序，得到各方案的优劣排序。

4 结束语

本文基于直觉模糊相似度的概念，提出一种新的直觉模糊相似度的计算方法。在直觉模糊环境下，采用直觉模糊数表示其相似度，较好地表现原始信息的模糊性不确定性，并在此基础上定义了广义直觉模糊有序加权扩展相似度（GIFOWES）算子，对其相关性质和各种特殊形式进行了研究。并基于此算子提出一种直觉模糊多属性决策方法，该方法不仅降低决策信息在集结过程的失真程度，而且为相似度的集结方法的研究提供一条有效途径。